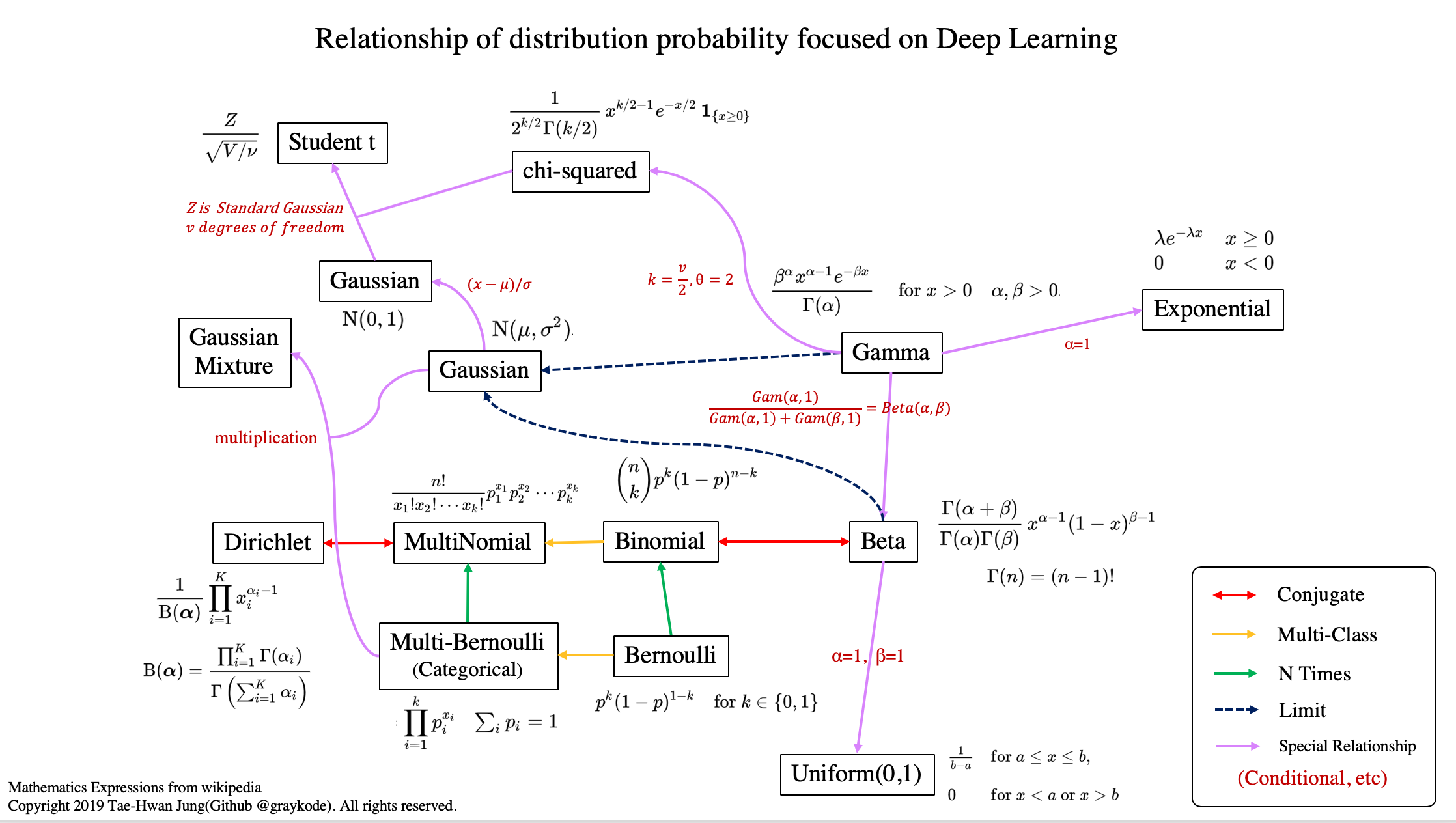
교재: Pattern Recognition & Machien Learning, Bishop
우측 블록링크 가독성은 박살을 내놨다 ㅎㅎ.. 죄송합니다
대학원 수업인 패턴인식론 수업의 마지막 과제를 진행하며
나중에 나한테도 도움이 될 것 같아 정리해본다.
(기재된 내용은 무조건 정답이 아니라, 공부한 내용을 적어뒀기 때문에 틀릴 수도 있습니다.)
잘못된 정보가 있다면 댓글 부탁드립니다.
1. Explain the meaning/concept of the following terms
1) Pattern Recognition (패턴인식)
패턴인식은 컴퓨터를 이용하여 데이터에 내재하는 패턴을 자동으로 추출하는 것을 의미
- 우리가 관찰한 데이터는 출현 가능한 데이터의 일부일 뿐이다.
- 우리에게 주어진 일부 데이터로부터 전체 데이터를 아우르는 패턴을 발견해야 한다.
따라서 이러한 패턴은 아직 발현되지 않은 데이터에 대해서도 잘 설명할 수 있어야 한다.
이것이 패턴인식의 목표이다.2) Machine Learning (머신러닝)
인공지능을 구현하는 대표적인 방법 중 하나
컴퓨터를 인간처럼 학습시킴으로써 컴퓨터가 새로운 규칙을 생성할 수 있지 않을까 하는 시도에서 시작되어 컴퓨터가 스스로 학습할 수 있도록 도와주는 알고리즘이나 기술을 개발하는 분야이다.
일반적으로 알고리즘을 이용하여 데이터를 분석하고, 분석 결과를 스스로 학습한 후, 이를 기반으로 어떠한 판단이나 예측을 하는 것을 의미한다.
따라서 양질의 데이터가 매우 중요한 역할을 한다.
3) Supervised Learning (지도학습)
입력 값과 함께 결과 값(정답 레이블)을 같이 주고 학습을 시키는 방법
- 분류(Classification) 데이터가 범주형 변수를 예측하기 위해 사용될 때
이미지에 강아지나 고양이와 같은 레이블을 할당하는 경우에 해당- 이진 분류(레이블 2개)와 다중 클래스 분류(레이블 여러 개)인 경우로 나뉜다.
- 회귀(Regression) 연속된 값을 예측할 때(시계열 데이터)
팔당댐 당류에 따른 서울시내 한강 주요다리 수위 예측
4) Unsupervised Learning (비지도학습)
정답을 알려주지 않고 예측하는 방법
정답을 모르더라도 유사한 것들과 서로 다른 것들을 구분해서 군집을 만들 수 있는 학습 방법
- 클러스터링(Clustering)
- 특정 기준에 따라 유사한 데이터 사례들을 하나의 세트로 그룹화 함
- 차원 축소(Dimension Reduction)
- 고려중인 변수의 개수를 줄이는 방법
아주 높은 차원의 특징을 가지는 원시 데이터(raw data)들 중 일부 특징들은 아무 관련이 없기 때문에 차원 수를 줄여서 관계를 도출함에 도움을 준다.
- 고려중인 변수의 개수를 줄이는 방법
5) Reinforcement learning (강화학습)
보상 및 벌칙과 함께 여러 번의 시행착오를 거쳐 스스로 학습하는 방법
- 주어진 상황에서 보상(reward)을 최대로 만드는 액션을 찾는 문제
- Supervised Learning과 다르게 타겟 값이 주어지지 않는다.
- 따라서, 많은 학습 시간이 필요하다.
Exploration과Exploitation의 trade-off 문제
6) Over-Fitting and Under-Fitting (과대적합, 과소적합)
- Under-Fitting
- 쉽게 말해 충분히 학습되지 않음 또는 모델이 너무 단순함을 의미함
- 이는 정확도가 낮다고도 할 수 있다.
- 쉽게 말해 충분히 학습되지 않음 또는 모델이 너무 단순함을 의미함
- Over-Fitting
- 그렇다고 너무 많이 학습 시키면 학습시킨 데이터 셋에 대해서는 높은 정확도를 보이지만, 새로운 테스트 데이터가 들어오면 정확도가 낮게 나오는 문제가 발생함
- 또는 데이터의 특성에 비해 모델이 너무 복잡한 경우도 Over-Fitting이 발생할 수 있다.
- MLP에서 Model에 들어가는 Parameter(Model Capacity)를 증가시키려면 Model 층(layer)를 더 많이 쌓거나, layer당 hidden unit 개수를 늘려야 하는데, 너무 많이(무한정)늘리게 되면 Over-Fitting이 발생한다.
7) Regularization term (정칙화)
학습할 때 모델에게 제약을 거는 방법
위 식에서 Loss function은 이며,
Regularization은 이다.
우리가 줄이고자 하는 것은 Loss function의 값이지만, 그렇다고 Cost가 줄어든다고 무조건 좋은 것이 아니다.(Over-Fitting의 문제)
그래서 이를 해결하고자 있는 것이 Regularization term이다.
만약 Cost를 줄일 때 특정 Parameter를 엄청 크게 만듦으로 인해 에러가 줄어드는 것이면 해당 작업을 하지 않도록 막아주는 역할.
→ 특정 값이 너무 커져 버린다는 뜻은 Over-Fitting이 일어나고 있다는 의미이다.
8) Entropy (엔트로피)
불확실성의 척도
- entropy가 높다는 것은 정보가 많고 확률이 낮다는 것을 의미
예시
동전을 던졌을 때 나올 수 있는 경우의 수:
주사위를 던졌을 때 나올 수 있는 경우의 수:
동전을 던지는 상황에 대한 entropy:
주사위를 던지는 상황에 대한 entropy:
동전의 entropy: 0.3010, 주사위의 entropy: 0.7782
주사위의 불확실성이 더 크다는 것을 알 수 있다.
이게 위에서 말한 정보가 많고 확률이 낮다는 것을 의미한다는 것
9) Frequentist view vs Bayesian view (빈도주의, 베이지안)
Frequentist: 모델에 대한 참 값이 있으며, 임의로 발생하는 것은 데이터이다.
모델의 파라미터에 대한 참 값이 있으며, 데이터가 랜덤으로 주어지는 것이다.
따라서 데이터에 대해서 이를 가장 잘 설명할 수 있는 단 하나의 모델을 찾아야 한다.
→ Likelihood를 최대화 하는 값을 찾는 것
Bayesian: 데이터가 참이며, 이를 가장 잘 설명하는 모델을 선택하는 것
반드시 모델에 대한 사전확률을 알아야 한다. (일어나지 않은 일에 대한 불확실성)
사전확률을 알기 위해서는 보통 샘플링을 통하는데,
의 식을 통해 확률이 최대가 되는 를 찾는다.
10) Cross Validation (교차검증)
머신러닝 평가에 필수적으로 사용됨
교차검증이 필요한 이유
우리는 데이터를 학습시킬 때 학습용 데이터인 Train Dataset과 평가용 데이터인 Test Dataset로 구성하게 된다.
만약 학습용 데이터인 Train Dataset을 Validation Dataset으로 분리하지 않으면 모델 검증을 위해서 Test Dataset을 사용해야 할 것이다.
결국 고정된 Test Dataset을 가지고 모델의 성능을 확인하며 파라미터를 수정하는 과정을 반복하게 되는데, 이렇게 되면 결국 Test Dataset에만 잘 동작하는 모델이 된다.(Over-Fitting이 된다.)
그래서 이를 해결하기 위해 Test Dataset을 중복없이 바꿔가면서 평가를 진행(교차검증)한다.
이렇게 되면 모든 데이터 셋을 평가 및 훈련에 활용할 수 있으며,
특정 데이터에 편중(Over-Fitting)을 막고, 데이터 부족으로 인한 Under-Fitting을 막을 수 있다.
교차검증의 종류들
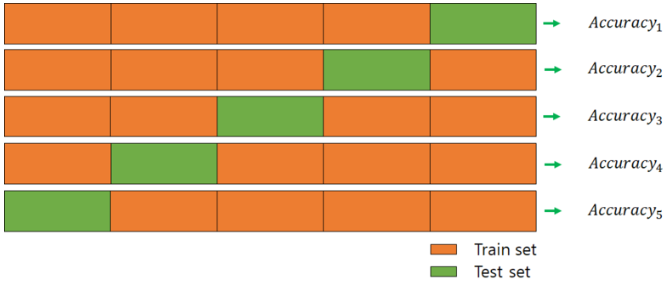
→ K-fold Cross Validation (일반적으로 사용되는 교차 검증 방법)
데이터를 k개의 데이터 폴드로 분할하고, 각 데이터 폴드 세트에 대해 나온 검증 결과들을 평균내어 최종적인 검증 결과를 도출하는 것
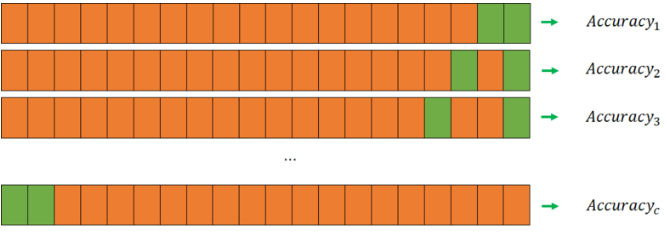
→ Leave -p- Out Cross Validation
전체 데이터 중에서 p개의 샘플을 선택해서 모델 검증에 사용하는 방법
이 방법도 마찬가지로 각 데이터 폴드 세트에 대해 나온 검증 결과들을 평균내는데,
이 방법은 경우의 수가 로 매우 크기 때문에 부담이 매우 크다
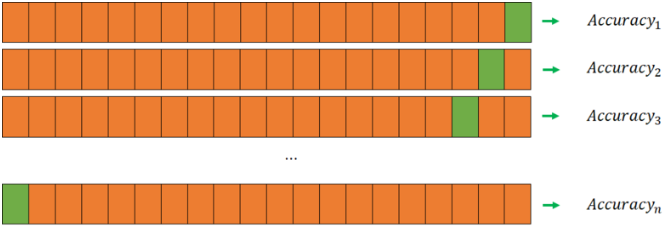
→ Leave -one- Out Cross Validation
Leave -p- Out Cross Validation보다 계산 시간에 대한 부담은 줄어들고, 더 좋은 결과를 얻을 수 있기 때문에 많이 사용된다.
모델 검증에 사용되는 데이터의 갯수가 단 1개이기 때문에 나머지 모든 데이터를 모델 훈련에 사용할 수 있는 것이 큰 장점이다.
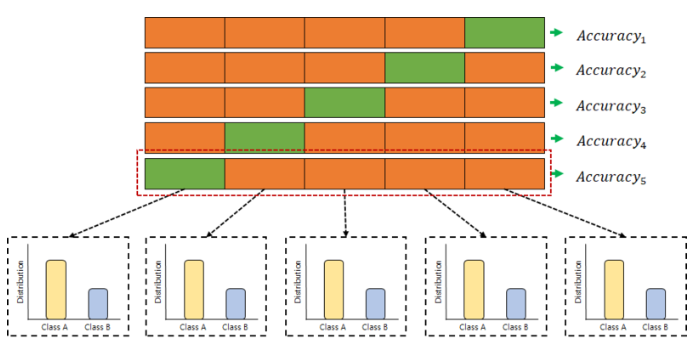
→ Stratified K-Fold Cross Validation
주로 분류(Classification) 문제에서 사용되며, label의 분포가 각 클래스별로 불균형을 이룰 때 유용하게 사용된다.
11) Curse of dimensionality (차원의 저주)
차원의 저주란 변수의 개수(수학적 공간 차원)가 늘어나면서, 문제 계산법이 지수적으로 커지는 상황을 말한다. (차원이 증가하면서 학습데이터 수가 차원의 수보다 적어지므로 개별 차원 내에서 학습할 데이터의 수가 적어지는 것이다.)
차원의 저주로 인해 알고리즘 모델링 과정에서 저장공간과 처리시간이 불필요하게 증가된다.
→ 이는 성능 저하를 의미한다.
물론 변수가 증가한다고 무조건 차원의 저주가 발생하는 것이 아니니 이 부분은 확실히 알아야 한다.
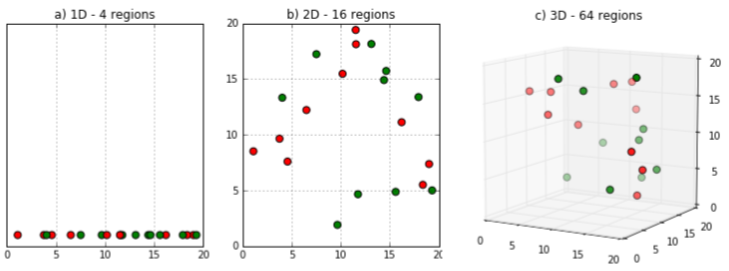
위 그림에서 보면 알 수 있듯이, 오른쪽으로 갈 수록(차원이 증가할 수록) 빈공간이 많이 생겨서 데이터가 서로 멀리 떨어져 있어서 새로운 샘플도 훈련 샘플과 멀리 떨어져 있을 가능성이 높다.
이를 해결하기 위해서는 훈련 샘플의 밀도가 충분히 높아질 때 까지 데이터를 추가하여 훈련 세트의 크기를 키우는 것이다.
하지만, 차원의 수가 커짐에 따라 필요한 훈련 샘플(데이터)의 수는 기하급수적으로 늘어난다.
그래서 현실적으로는 PCA와 같은 차원 축소 기법을 이용해서 차원의 저주 문제를 해결한다.
12) Regression vs Classification (회귀, 분류)
지도학습에 사용되는 이 둘은 비슷한 개념이지만 서로 다른 종류의 출력값을 내놓는 모델을 학습하는데 차이를 둔다.
우리가 사용하는 데이터는 이산적인(Discrete)값을 가지거나, 연속적인(Continuous)값을 가지는 데이터로 나눌 수 있다.
Regression(회귀)
- 예측값으로 연속적인(Continuous) 값을 출력
- 비가 올 확률, 날짜에 따라 변한 데이터에 대한 예측등은 회귀
Classification(분류)
- 예측값으로 이산적인(Discrete) 값을 출력
- 강아지인지 고양이인지를 나누는 것은 분류
13) Bayes theorem (베이즈 정리)
이전의 경험과 현재의 증거를 토대로 어떤 사건의 확률을 추론하는 과정
베이즈 정리는 확률 를 알고있을 때, 를 계산하기 위해 등장함.
= 의 사전 확률(evidence), 현재의 증거
= 의 사전 확률(prior probability), 과거의 경험
= 사건 가 주어졌을 때 의 조건부 확률(likelihood)
= 사건 라는 증거에 대한 사후 확률(porsterior probability)
베이즈 정리의 가장 큰 특징은 결과를 관측한 뒤 원인을 추론할 수 있다는 것이다.
14) Conjugate prior
베이즈 정리 식은 아래와 같다.
여기서 사후확률인 Posterior를 구하는 것이 문제인데, Bayesian으로 Posterior를 계산한다고 할 때, 각 항목이 일반적인 분포를 따르지 않는다고 하면 도출 방식이 매우 복잡해 질 수 있다.
반대로 likelihood가 특정 분포를 따른다고 가정할 때, Prior와 Posterior가 동일한 분포를 따르면 계산이 매우 편해진다는 것이다.
그래서 이렇게 Prior와 Posterior가 동일한 분포를 따를 수 있도록 하는 것이 Conjugate Prior이다.
→ Conjugate Prior를 사용하면 베이즈 정리 식을 단순화할 수 있다는 의미
15) Beta distribution (베타 분포)
이항분포에서 발생한 Over-Fitting을 해결하기 위해 나온 분포
베타분포는 베이지안 방법에서 이항 분포의 켤레 사전 분포(Conjugate Prior Distribution)로 활용됨.
관측사건 이벤트가 오기 전에 평균값에 추가 해 주는 것.
→ 이게 무슨 뜻이냐면, 아래 사진에서 prior와 likelihood를 더하면 posterior값이 나온다는 것이 베타분포이다.
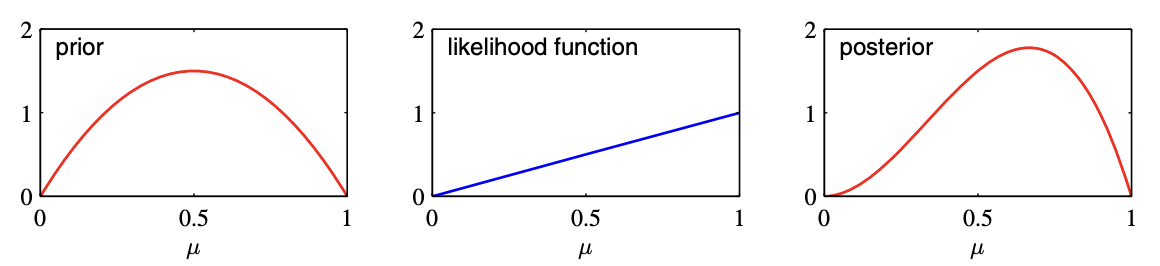
예시
동전 3번을 던져서 앞면이 연속으로 3번 나왔으면, 이 동전은 무조건 앞면만 나오는 동전인가?
아니다, 이것이 과적합. 그래서 이걸 해결하기 위해 원래 확률이 얼마나 나오는지 사전에 정해주는 것
16) Central limit theorem (중심극한정리)
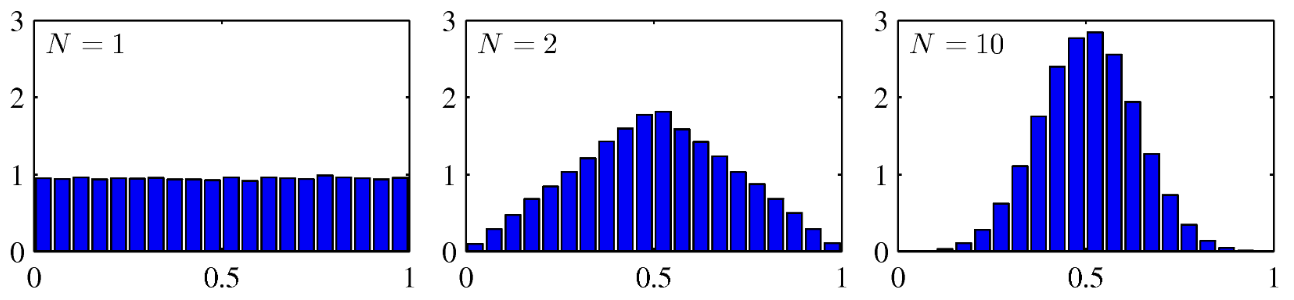
가우시안 분포에서 가장 중요한건 중심극한정리이다.
위 사진에서 N은 관찰 값이다. ex) 동전을 던졌을 대 앞이 나올 확률과 뒤가 나올 확률 값
이면 동전을 한번만 던졌을 때 평균 값이고, 이면 10번 던졌을 때 평균 값이다.
→ 동전을 던졌을 때 앞/뒤가 나올 확률은 50%니까 많이 던질수록 정확한 값이 나온다.
따라서, 표본의 크기가 커질수록(보통 30이상) 정규분포에 가까워진다는 정리이다.
17) Nonparametric distribution (비모수적 분포)
관측 값이 어느 특정한 확률분포 ex) 정규분포, 이항분포등을 따른다고 전제할 수 없거나, 모집단에 대한 아무런 정보가 없는 경우, 소규모에 실시하는 검정 방법이다.
보통 모집단의 분포가 대칭이라거나, 중앙값이 어디인지 등의 가정을 하는 것이 보통이다.
즉, 자료가 관측치 자체보다 부호나 순위만이 의미가 있는 경우에 자주 이용된다.
18) Sequential Learning (순차 학습)
MLE 기법은 전체 데이터를 한번에 사용해서 처리하는 batch방식이다.
하지만, 데이터 규모가 커지거나, 데이터가 순차적인 입력으로 주어질 때는 한번에 사용해서 처리하는 batch방식을 사용하기 힘들다.
따라서, 데이터가 순차적으로 입력될 때 에러함수 를 로 정의하여 파라미터가 업데이트 되도록 만든다. (Stochastic Gradient Decent라는 방식인데, Sequential Learning이라고 한다.)
이러한 형태의 알고리즘을 LMS(least mean square)이라고 한다.
19) Fisher’s Linear discriminant (피셔의 선형 분류법)
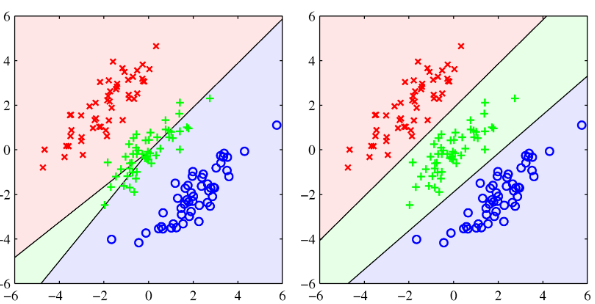
왼쪽: 최소제곱법 사용, 오른쪽: 로지스틱 회귀 사용
타겟 벡터가 가우시안 조건부 분포를 가지고 있다는 가정을 하고 있기 때문에 3차원 클래스 분류 문제에서도 최소제곱법은 정확하지 않다. 그래서 나온 분류볍이 피셔의 선형 분류법이다.
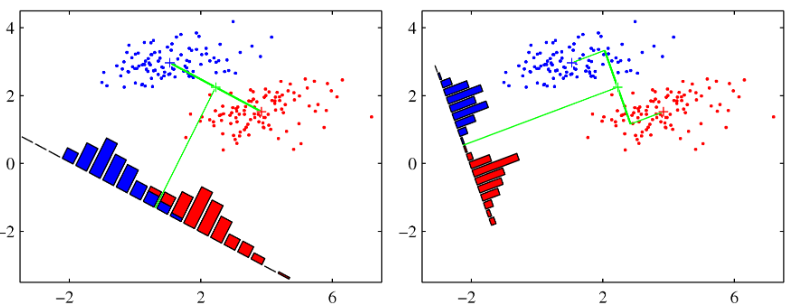
위 사진을 보면 직관적으로 봐도 오른쪽이 낫다. (오른쪽이 피셔의 선형 판별식)
→ D차원의 데이터를 1차원의 축으로 투영하되, 같은 클래스 내의 데이터끼리는 최대한 모여있고, 다른 클래스를 가지는 데이터끼리는 최대한 떨어져 있도록 할 수 있는 1차원 벡터를 구하는 것
20) Perceptron (퍼셉트론)
다수의 입력으로부터 하나의 결과를 내보내는 알고리즘
→ 실제 뇌를 구성하는 신경세포뉴런의 동작과 유사하다.
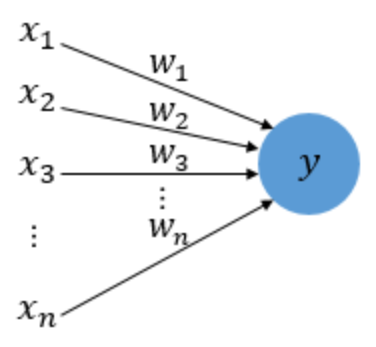
입력값에는 각각의 가중치가 존재하는데, 이 때 가중치의 값이 크면 클수록 해당 입력값이 중요하다는 것을 의미한다.
2. Suppose that the two variabels and are statistically independent. Show that the mean and variance of their sum satisfies
- 두 확률 변수 의 합의 분산은 각 확률 변수의 분산의 합과 다음과 같은 관계가 있다.
(마지막 항은 양수/음수가 될 수 있다.)
- 확률 변수 x + y의 기댓값은 기댓값의 성질로부터 각 확률 변수의 기댓값의 합과 같다.
- 분산의 정의와 기댓값의 성질로부터 다음이 성립한다.
- 두 확률 변수 가 서로 독립이라면 의 식이 일치한다.
- 이 등식을 이용하면 서로 독립인 두 확률 변수의 합의 분산은 각 확률 변수의 분산의 합과 같다는 것을 볼 수 있다.
- 이 등식을 이용하면 서로 독립인 두 확률 변수의 합의 분산은 각 확률 변수의 분산의 합과 같다는 것을 볼 수 있다.
3. Describe three types of distinct approaches to solving decision problem
Minimizing The Misclassification Rate (오분류 최소화)
- 의사결정의 목적은 잘못된 분류 가능성을 최대한 줄이는 것
- 따라서 모든 에 대해서 특정 클래스로 할당시키는 규칙이 필요하다.
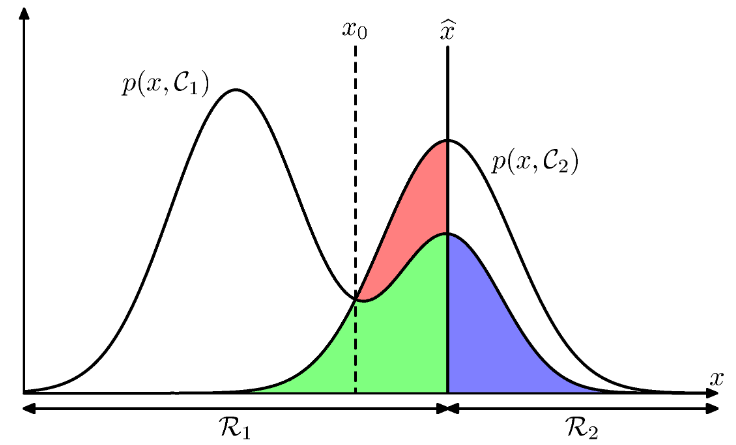
- 현재 클래스의 구분선을 라고 결정 할 경우
- 인 영역에서는 해당 클래스가
- 인 영역에서는 해당 클래스가
- 이렇게 하면 에러의 합은 청색, 녹색, 적색이 된다.
- 이를 최소화 하는 영역으로 기준선을 변경해야 하는데, 최소화 하는 지점은 이다.
Minimizing The Expected Loss (기대 손실 최소화)
- 오분류 최소화 방법만으로는 오분류의 수를 줄이기엔 부족하다.
- 예를 들어 암 진단에 대한 오분류의 경우를 생각해보자.
- case1: 암이 아닌데 암인 것으로 진단
- case2: 암이 맞는데 암이 아닌 것으로 진단
- case1보다 case2가 더 심각하기 때문에 모델에 이러한 정보(패널티)를 주기 위해 생긴 개념인
Loss function이 등장
- 이 식 자체를 에러함수로 정의해서 사용하면 된다.
The Reject Option (리젝트 옵션)
- 사후 확률 또는 결합 확률 이 1에 가까운 값이 아니라
클래스별로 비슷한 경우 이 에 대해 분류했을 대 에러는 커진다. - 이러한 범위에 존재하는 에 대해 특정한 클래스로 할당하는 것이 부담일 수 있다.
이런 경우 결정을 회피하는 기능을 Reject Option이라고 한다.
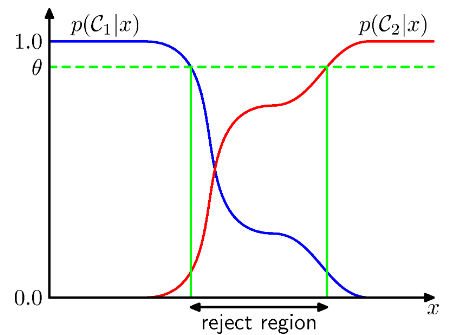
- 위 그림에서 보면 알 수 있듯, 사후 확률 값이 특정 수준(threshold)에 미치지 못하면 클래스 분류를 보류하는 것이다.
4. Describe the mixture of Gaussians and its meaning
가우시안 분포가 아주 흔하게 사용되는 분포이긴 하지만 현실적으로 가우시안만을 적용하기 어려운 경우가 생겨나기도 한다.
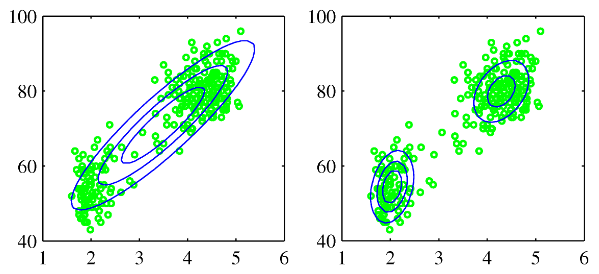
위 사진은 옐로스톤 국립공원에 있는 올드 페이스풀 간헐천의 화산 폭발에 대한 측정 데이터이다.
- 가로축: 다음 폭팔까지의 시간
- 세로축: 폭발 지속시간
데이터 집합은 크게 두 개의 지배적인 집단을 형성하고 있는데, 가우시안 분포로는 이를 구성할 수 없다.
- 왼쪽 그림은 하나의 가우시안 분포로 데이터를 표현한 것이고, 오른쪽 그림처럼 표현해야 함
→ 두 개의 가우시안 선형 중첩이 더 나은 표현 방식이 될 수 있다.
이러한 문제를 해결하기 위해 혼합 가우시안 모델이 나왔다.
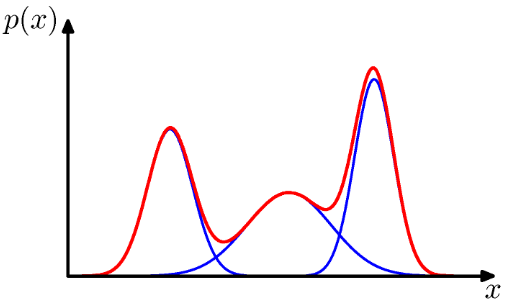
가우시안 선형 결합을 통해 매우 복잡한 밀도를 표현할 수 있다.
→ 선형 결합의 계수 뿐 아니라 평균과 공분산 파라미터를 조절함으로써 거의 대부분의 연속 밀도를 임의의 정확도로 근사가 가능하다.
- 혼합 가우시안 분포의 파라미터는 이며, 파라미터 값을 설정하기 위해 MLE를 사용한다.
- 미분을 취해 최대값을 가지는 모수를 찾는 방식이 아니라 반복적 수치 최적화 기법이 요구된다.
5. Explain the difference between Maximum Likelihood Estimation and Maximum A Posterior and describe what they mean
최대우도추정(MLE)
현재 가지고 있는 데이터셋이 나올 확률을 최대화하는 우도(Likelihood)를 구하는 것
는 를 최대로 하는 이고 최종식은 이다.
결국 에 영향을 미치는 것은 와 의 비율이다.
또한 이건 추정값이기 때문에 실제값과 오차값이 있다.
오차의 범위를 구하는 식은 이다.
최대사후확률추정(MAE)
데이터셋이 나올 확률을 최대화 하는 것이 아닌, 사후확률(Posterior)인 를 최대화 하는 것
는 상수이므로 위 식을 아래와 같이 변형 해도 의 값은 변하지 않는다.
여기서 최대 우도 추정에서와 동일하게 이하의 식에 로그를 취하고, 미분하여 그 값이 0이 되는 를 찾은 최종식은 이다.
최대우도추정(MLE)과 최대사후확률추정을 통해 추정한 특정 사건의 확률 는 비슷한 모양새를 띠고 있지만, 베타분포 내의 상수가 일 경우에만 같아진다.
하지만, 시행횟수 이 커지면, 데이터셋의 크기가 커질수록 상수인 에 비해 가 커지게 되기 때문에 이 커질수록 최대우도추정으로 구한와 최대사후확률추정으로 구한가 비슷해진다.
6. Describe the algorithm of the perceptron
퍼셉트론은 인공신경망(ANN)의 구성요소(unit)로써 다수의 값을 입력받아 하나의 값으로 출력하는 알고리즘이며, 이진분류 모델을 학습하기 위한 지도학습 기반의 알고리즘이다.
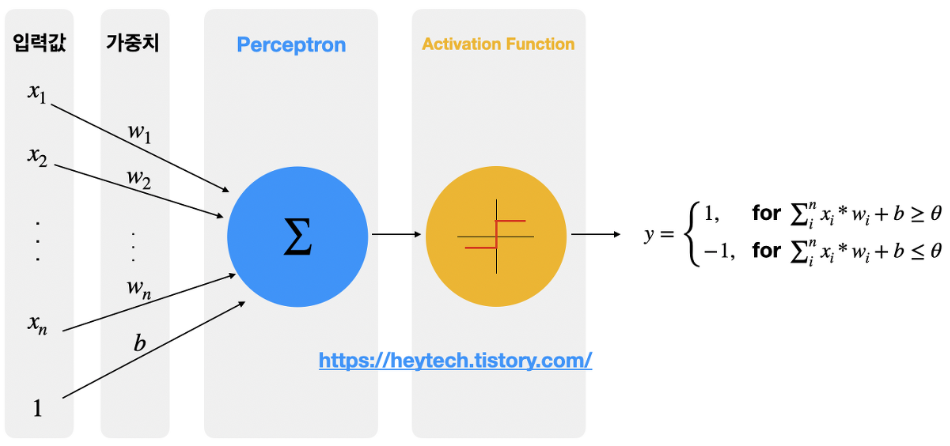
퍼셉트론은 다른 뉴런으로부터 신호를 입력받듯, 다수의 값 를 입력받고,
입력된 값마다 가중치(를 곱한다.
입력값으로 외에도 편향(은 딥러닝 모델 최적화의 중요 변수 중 하나이다.
일반적으로 입력값을 1로 고정하고 편향을 곱한 변수로 표현하는데,
이 때 입력값과 가중치의 곱, 편향은 퍼셉트론으로 전달된다.
퍼셉트론은 입력받은 값을 모두 합산하는데, 합산된 결괏값을 가중합이라 부른다.
퍼셉트론에서는 가중합의 크기를 임계값(, Threshold)과 비교하는 활성화 함수(Activation Function)를 거쳐 최종 출력값을 결정한다.
가중합의 크기는 편향의 크기로 조절할 수 있기 때문에, 편향이 퍼셉트론의 출력값 를 결정짓는 중요한 변수이다.
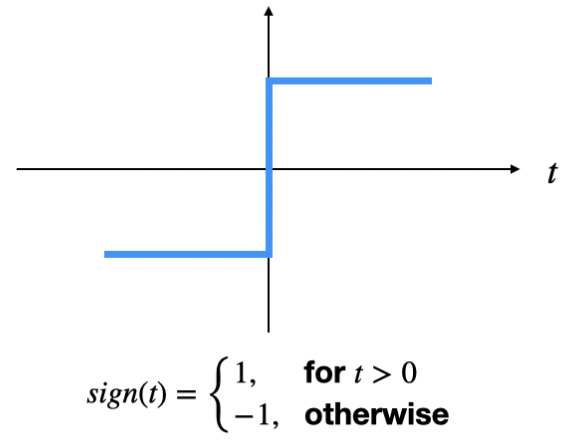
인공신경망과 다르게, 퍼셉트론은 활성화 합수로 계단 함수(Step Function)을 사용한다.
계단 함수의 일종인 함수를 사용하면 가중합이 임계값보다 클 경우 을 출력하고, 그렇지 않다면 을 출력한다.
퍼셉트론의 종류
- 은닉층이 있으면 단층 퍼셉트론(Single-Layer)
- 단층 퍼셉트론은 출력값을 구분짓는 직선을 1개밖에 그리지 못하기 때문에
XOR 게이트를 구현할 수 없다.
- 단층 퍼셉트론은 출력값을 구분짓는 직선을 1개밖에 그리지 못하기 때문에
- 은닉층이 없으면 다층 퍼셉트론(Multi-Layer-Perseptron, MLP)
- XOR게이트를 구현하지 못하는 단층 퍼셉트론의 한계를 보완하기 위함
- XOR게이트를 구현하지 못하는 단층 퍼셉트론의 한계를 보완하기 위함
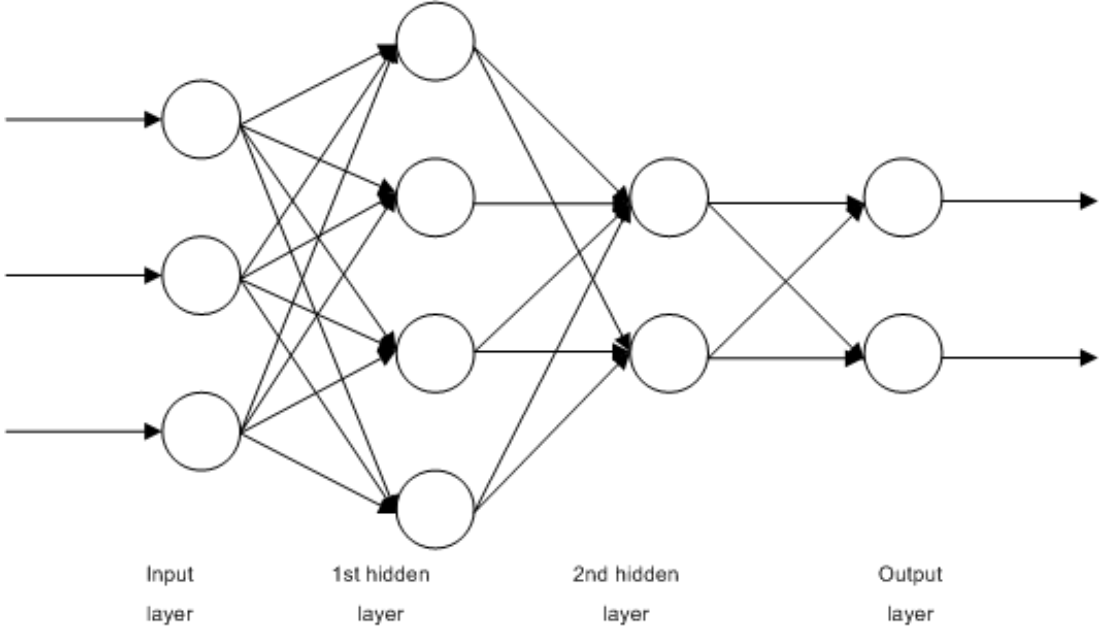
→ 일반적으로 2개 이상의 은닉층을 가진 다층 퍼셉트론을 심층신경망(DNN)이라고 함
퍼셉트론 수렴 법칙
- 정확한 해법이 있다는 조건에서는 일정 횟수를 반복하면 정확한 해법을 찾을 수 있다.
- 실제 수렴하기까지 요구되는 단계의 수는 알기 어렵다.
- 실제 데이터가 수렴 가능한 조건일지라도 여러 해법이 존재한다.
파라미터 초기값에 의존하는 알고리즘데이터 순서에 의존하는 알고리즘
- 퍼셉트론의 출력값은 확률값이 아니다.
- 중요한 제약 중 하나는 고정된 기저함수의 선형 결합을 기반으로 한다는 것이다.
7. Aside from the above, describe three topics in your textbooks that you are most interested in, deeply influenced by, or consider important
1. Minimizing The Misclassification Rate (오분류 최소화)
기본적으로 분류에 있어 목적은 어찌보면 잘못된 분류 가능성을 최대한 줄이는 것이다.
따라서 모든 에 대해서 특정 클래스로 할당시키는 규칙이 필요하다.
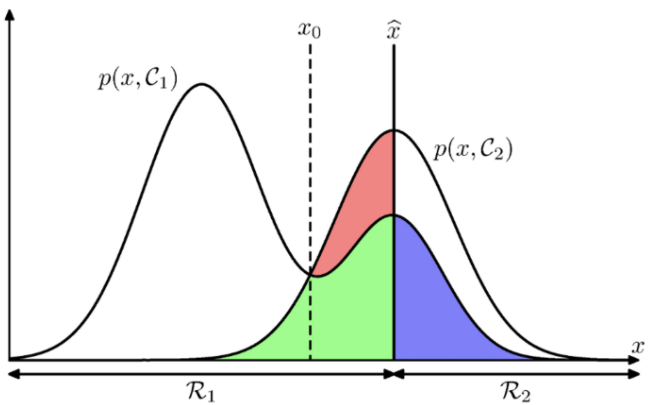
위 사진을 보고 쉽게 이해해보자.
- 현재 클래스의 구분선을 으로 결정했다고 가정하게되면
- 영역은 로 결정되고, 영역은 로 결정된다.
- 빨간색 부분의 에러를 지워야하는데, 초록색 부분이 줄어들면 오히려 좋다.
왜냐하면, 원래 인데, 으로 오분류 했던 부분이기도 하고,
빨간색 부분의 오분류와 함께 줄어들기 때문이다. - 따라서 면적을 최소화 하는 방법은 인 지점이다.
2. The Perceptron Algorithm (퍼셉트론 알고리즘)
신경망 등에서 사용되는 알고리즘이며, 아주 간단한 형태의 binary class 퍼셉트론만 확인한다.
여기서는 기저함수를 넣어 로 표현하며, 이다.
- 기저함수를 사용하는 이유는
feature vector때문이다.- feature vector란?
예시로 3 x 3(2차원) → 9(1차원)으로 변환하여 원래있던 데이터를 잘 표현하는 것이다.
기저함수가 음성영역에서는 FFT, 딥러닝에서는 인코딩 벡터라고 생각하면 된다.
- feature vector란?
- 퍼셉트론 알고리즘에서 는 활성함수로, 가장 간단한 형태는 아래와 같다.
- 퍼셉트론에서도 (가중치)를 구하는것이 주 목표이다.
- 오분류된 데이터의 수만 가질 때 퍼셉트론 알고리즘에서는 에 대해 상수값을 가지고,
불연속적인 값을 가지게 되므로 미분이나 Gradient 방식을 사용할 수 없다.
따라서 에러함수의 경우 아래와 같이 정의하게 된다.
- 앞에 가 붙은 이유
- 또는 이 둘 다 이거나 일 때가 잘 분류 된 상태인데, 오분류 되면 둘 중 하나가 이기 때문에 가 되는 때를 오분류된 때라고 판단하기 위해
- 이런식으로 정의하면 오분류된 샘플이 없을 때 에러 함수 값이 0이 되고, 그 외에는 값이 커진다.
- 정의
- = 오분류된 데이터 집합
- 만약 이 에 속한다면
- 만약 이 에 속한다면
3. Probabilitic Generative Models (확률 생성 모델)
왜 생성(Generative) 모델인가?
부터 시작하는지, 부터 시작하는지에 따라 생성모델인지, 사후분포를 따라가는지가 나뉜다.
부터 시작하면 생성모델이다.
위 식에서 이란?
= class-conditional(조건부 밀도)
= prior(사전 분포)
binary class에 한해서 이다.
여기서 는 class에 속한 하나의 데이터이다.
위 식에서 는 로지스틱 시그모이드 함수이다.
는 sigmoid를 뜻한다.
만약 multi class라면 아래 식과 같이 표기할 수 있다.
위 식은 같은 의미이지만 3가지로 불린다.
- normalized exponential 함수
- 다중 클래스 분류에 사용되는 시그모이드 함수
softmaxfunction
여기서 알 수 있다. 딥러닝에서 이진분류를 쓸 때는 sigmoid, 다중분류를 쓸 때는 softmax를 사용해서 코드를 작성하는 이유가 위 식에 따른 이유이다.
단, 미세한 조정이 필요한 경우에는 평활화(Smooth)작업이 필요하다.
결과적으로 multi class에서 사용하게 되면 이다.
학습에 가장 중요했던 (1차원 방정식)이랑 매우 유사한 것을 알 수 있다.
원래 인공지능이 가정을 하면서 추론을 하는 것이기 때문에 그런 것을 기억하자.
참고자료
- PRML (norman3.github.io)
- (5) Model Capacity (tistory.com)
- [Deep Learning] Regularization — 심심한 개발 블로그 (tistory.com)
- [머신러닝] 손실함수(loss function) (2) - 엔트로피(Entropy) (tistory.com)
- Frequentist vs Bayesian (tistory.com)
- 교차 검증(cross validation) : 네이버 블로그 (naver.com)
- 차원의 저주 개념, 발생 원인과 해결 방법 (tistory.com)
- 머신러닝 - 회귀(Regression) VS 분류(Classification) (tistory.com)
- [확률과 통계] 14. 베이즈 정리, Baye.. : 네이버블로그 (naver.com)
- Conjugate Prior에 대하여 :: 미니의 꿈꾸는 독서, 그리고 프로그래밍 이야기 (acronym.co.kr)
- 07-01 퍼셉트론(Perceptron) - 딥 러닝을 이용한 자연어 처리 입문 (wikidocs.net)
- 7.3 분산과 표준편차 — 데이터 사이언스 스쿨 (datascienceschool.net)
- 최대 우도 추정 & 최대 사후 확률 추정 (MLE & MAE) · Data Science (yngie-c.github.io)
- [Deep Learning] 퍼셉트론(Perceptron) 개념 이해 (tistory.com)