게임을 하다보면, 내 캐릭터 위치를 이동시키기 위해 어딘가 위치를 찍게 된다.
그럼, 내 캐릭터는 어떤 알고리즘으로 그 위치를 정확하게 찾아가는 걸까?

최단경로 알고리즘의 종류와 시간복잡도

1. 플로이드 알고리즘 (Dynamic Programming, $O(N^3)$)
2. 다익스트라 알고리즘 (Greedy Approach, $O(N^2)$)
3. A* 알고리즘 (Heuristic Alrogithm, $?$)

• 구현 방식에 따라 시간복잡도가 달라짐, 다익스트라의 확장판
  출발 지점에서 목적 지점까지 가면서 주변에 새로 검색되는 지점들을 모두 Priority-Queue(우선순위)에 넣고, 그 중에서 Top Priority 지점을 꺼낸 후, 그 지점부터 다시 주위로 검색을 반복함

4. JPS 알고리즘 (Jump Point Search, ?)

• A* 알고리즘과 큰 구조는 같으나, 레이더처럼 방사 형태로 검색을 하고, 충돌 정보를 기반으로 분기점이 될 수 있는 지점들만 Priority-Queue에 넣기 때문에 탐색거리가 멀어질수록, A*보다 빠른 경로 탐색 결과를 도출한다.
  JPS(B) 알고리즘의 경우 A*보다 1000배 이상 빠르다는 이야기도 있다..

BFS, 벨만포드 등도 있지만 그냥 대표적인 것들만 적어두었다.

JPS 알고리즘이 성능이 더 좋은건 맞지만 동서남북 4방향이 아닌 8방향의 대각 방향을 보기 때문에 코딩테스트 문제에서는 거의 사용되지 않는다.
따라서 A*알고리즘에 대해 알아보자 (물론 A*도 8방향을 볼 수는 있다.)

A* 알고리즘

• A* 알고리즘은 내가 출발해야하는 지점과 도착해야하는 지점을 알아야 사용할 수 있다.
  • dijkstra 알고리즘은 출발 지점만 알아도 되지만, 모든 경로를 탐색하기 때문에 불필요한 탐색이 발생할 수 있다.

• A* 알고리즘은 다음 탐색 노드를 선정하는 방식이 다른 최단거리 탐색 알고리즘들과는 약간 다르다.

  • $F(n) = G(n) + H(n)$의 식을 따르는데, 각 역할은 아래와 같다.
    • $F$ = 해당 노드 $n$에 대한 가중치들의 합
    • $G$ = 새로운 노드까지의 거리
    • $H$ = 현재지점으로부터 도착지점까지의 예상 가중치
  • 여기서 제일 중요한 건 $H$다.
    • $H = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$로 구할 수 있다.
      $(x_1, y_1)$ = 시작지점 좌표
      $(x_2, y_2)$ = 도착지점 좌표
      이 식은 그냥 점과 점 사이 거리를 알기 위한 공식이다.

• Open-List와 Closed-List

  • Open-List: 탐색 가능성이 있는 노드들의 집합
  • Closed-List: 탐색이 완료된 노드들의 집합

• 동서남북 중 한 칸을 이동할 때의 비용: 10
• 대각으로 한 칸을 이동할 때의 비용: 14
  로 두는게 좋다. 왜냐면 피타고라스 정리에 따라 삼각형의 변을 구하는 공식을 따라가기 때문.
  $\begin{aligned} a^2 + b^2 &= c^2\\ 10^2 + 10^2 &= 14^2 \end{aligned}$
  근데 $10^2 + 10^2 = 200$이고, $14^2 = 196$인데 이게 어떻게 같냐?
  라고 할 수 있는데, 정확히는 틀린 값이지만, 최단경로를 찾기 위해서는 실수형이 아닌 정수형이어야 처리속도가 훨씬 빨라 비슷한 값으로 쓰는 것이다.

A* 알고리즘의 처리 순서

1. 출발 노드를 Open-List(Queue)에 삽입
2. Open-List에서 pop()하여 비용 평가
3. Closed-List에 삽입

위 3개를 종료노드까지 반복하면 된다.

---

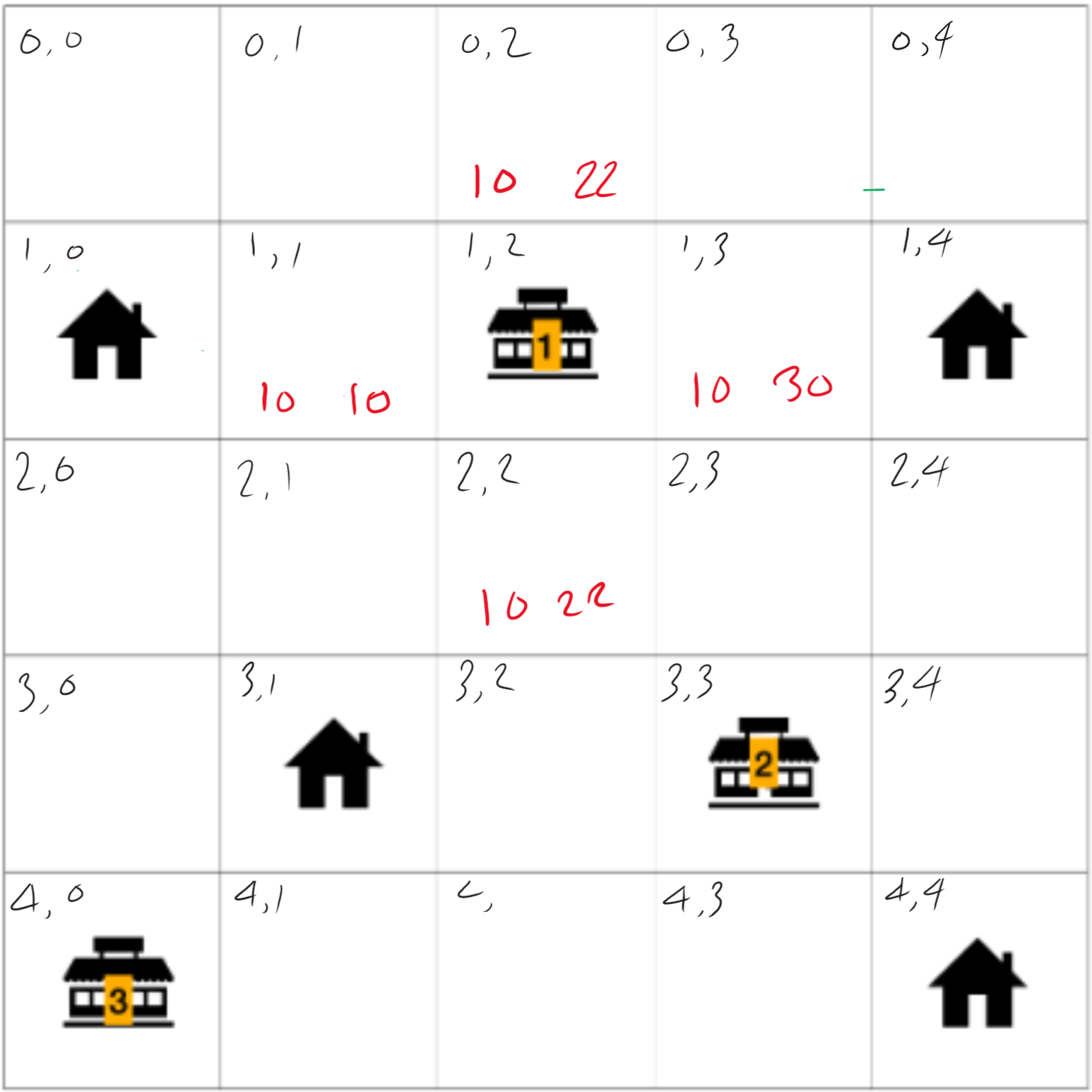
코딩테스트 문제로 알아보기

삼성 2022년도 하반기 오후 1번문제

CODETREE - 코드트리빵 골드2

각 줄에 주석을 달아두었으니 이해해보자.

import sys, math

input = sys.stdin.readline

# 격자 크기, 빵 사러 갈 사람의 수
N, M = map(int, input().split())
# 격자 받아오기
area = [list(map(int, input().split())) for _ in range(N)]
# 편의점 위치 받아오기
store = [list(map(int, input().split())) for _ in range(M)]

# A* 알고리즘에 필요한 변수
F, G, H = 0, 0, 0

# A* 알고리즘을 진행하며 지나가지 못하는 부분을 만들어 줄 벽
wall = []

# 빵사러 갈 사람들의 최단거리 수
path_length = [0]*M

# basecamp 좌표 저장을 위한 리스트
basecamp = []

# basecamp 좌표 저장
for i in range(N):
    for j in range(N):
        if area[i][j] == 1:
            basecamp.append([i, j])

# store 위치 재 조정(-1씩 해줘야 한다.)
for idx in range(len(store)):
    sx, sy = store[idx]
    store[idx] = [sx-1, sy-1]

# 점과 점 사이를 알기 위한 식 사용(F, G, H중 H에 해당)
def heuristic(x1, y1, x2, y2):
    return int(math.sqrt(((x2-x1)**2) + ((y2-y1)**2))*10)

# A* 알고리즘 실행
def astar(f, g, h, x1, y1, x2, y2):
    # 남 동 서 북
    dx = [1, 0, 0, -1]
    dy = [0, 1, -1, 0]

    buffer = []
    # 한 칸 이동할 때마다 10씩 줌
    g += 10
    # 남 동 서 북 순으로 4번 반복해서 각 위치에 대한 가중치 구하기
    for x, y in zip(dx, dy):
        nx1, ny1 = (x1+x), (y1+y)
        # 만약 이동하려는 곳이 닫힌 리스트(체크한 리스트)에 있는 곳이라면 넘어감
        if (nx1, ny1) in closed_list:
            continue
        # H 가중치 구하기
        h = heuristic(nx1, ny1, x2, y2)
        # 가중치 합산
        f = g + h
        # 합산된 가중치 buffer에 잠시 저장 (4점 비교를 위해)
        buffer.append([f, (nx1, ny1)])
    # 가장 작은 값을 new x, new y변수에 저장
    nx, ny = min(buffer)[1]
    # 가장 작은 값을 open_list에 저장
    open_list.append((nx, ny))
    return nx, ny

# 가고싶은 편의점에서 가장 가까운 베이스캠프 탐색 (반대로 탐색함)
## astar 알고리즘을 사용하려면 정확한 출발지점과 도착지점이 있어야 함
### 출발 지점은 편의점
for user, (sx, sy) in enumerate(store):
    # 벽을 생성하기 위한 임시 변수
    wall_buffer = []
    # 도착 지점은 베이스캠프
    for bx, by in basecamp:
        # 만약 출발지가 벽이라면(이미 지나갔었다면) 넘어감
        # 또는 도착지가 벽이라면(이미 지나갔었다면) 넘어감
        if (sx, sy) in wall or (bx, by) in wall:
            continue
        # 이동 가능한 좌표 저장을 위한 변수
        open_list = []
        # 이동이 완료된 좌표 저장을 위한 변수
        closed_list = []
        # 출발지점은 계속 변경 될 예정이기 때문에 새로 변수 선언
        nsx, nsy = sx, sy
        # 출발지점을 open_list에 넣고
        open_list.append((nsx, nsy))
        # 바로 빼서 closed_list에 넣음
        closed_list.append(open_list.pop())

        # astar 알고리즘 반복 실행
        while True:
            # 출발지점을 제일 가중치가 낮은(가까운) 곳으로 변경
            nsx, nsy = astar(F, G, H, nsx, nsy, bx, by)
            # 이동했던 좌표를 closed_list에 넘김
            closed_list.append(open_list.pop())
            # 만약 이동하려는 좌표가 도착지라면(목적지에 도착했다면) 반복문 종료
            if (nsx, nsy) == (bx, by):
                break
        # 이동했던 경로를 벽을 생성하기 위한 임시 변수에 저장
        wall_buffer.append(closed_list)        

    # 최종적으로 어떤 경로를 선택할 건지 저장하기 위한 변수
    check_path = []
    # 여러 경로들 중, 최적의 경로 1개만 선택하기 위한 반복문
    for wb in wall_buffer:
        # 만약 경로가 비어있다면(처음이라면)
        if check_path == []:
            check_path = wb
        else: # 경로가 비어있지 않다면
            if len(check_path) == len(wb): # 최단거리 같을 때
                if check_path[-1][0] == wb[-1][0]: # 행이 같을 때
                    if check_path[-1][1] > wb[-1][1]: # 비교하려는 열 값이 더 작다면
                        check_path = wb # 바꾸기
                else: # 행이 다를 때
                    if check_path[-1][0] > wb[-1][0]: # 비교하려는 행 값이 더 작다면
                        check_path = wb # 바꾸기
            elif len(check_path) > len(wb): # 비교하려는 최단거리가 더 작을 때
                check_path = wb # 바꾸기

    wall.append(check_path[0]) # 편의점(출발지점) 벽으로 세움
    wall.append(check_path[-1]) # 베이스캠프(도착지점) 벽으로 세움
    path_length[user] = len(check_path) # user 순서대로 몇칸 움직여야하는지 값 넘겨주기

# 시뮬레이션 (최단거리를 유저 순으로 진행했을 때)
count, time = 1, 1
while sum(path_length) != len(path_length):
    for i in range(count):
        if path_length[i] > 1:
            path_length[i] -= 1
    if count < M:
        count += 1
    time += 1

# 최종 걸린 시간 출력
print(time)