Chapter 5. Trees

지환·2022년 4월 12일
DS - Horowitz
0

중요한 data object인 Tree에 대해 알아보자

5.1 Introduction

5.1.1 Terminology

Definition
: A tree is a finite set of one or more nodes such that
(1) There is a specially designated called the "root"
(2) The remaining nodes are partitioned into n≥0 disjoint sets T1, ..., TnT_1,\ ...,\ T_n, where each of these sets is tree. T1, ..., TnT_1,\ ...,\ T_n are called subtrees of the root.

T1, ..., TnT_1,\ ...,\ T_n가 disjoint set 이라는 조건은, 각 subtrees끼리는 연결되지 못한다는 소리다.
또 tree의 모든 node는 특정 subtree의 root가 될 수 있다.(끝 node는 본인이 root이고 subtree가 없는 경우이다.)

각 node의 subtree 숫자를 drgree라고 한다.(아래로 내려가는 level이 더 낮은 subtree 숫자를 말한다.)
위의 경우 A의 degree는 2이고, E는 1이다.
Degree of a tree는 해당 tree node의 degree 중 가장 큰 degree를 말한다.

degree가 0인 node를 leaf or terminal nodes라고 부른다.
(나머지는 nonterminal)

node X의 subtrees의 roots를 node X의 children이라고 한다.
반대로 X는 해당 children의 parent이다.
parent가 같은 children을 sibling이라고 한다.
특정 node X로부터 root까지 이어진 모든 node를 X의 ancestors라고한다.(root포함)

root가 특정 level n이라면, 그 children은 n+1, ... 이런식으로 간다.
(누구는 root level을 0으로하고, 누군 1로함.)
height나 depth는 가장 큰 level을 말한다.

추가 설명

트리(나무위키)

Data Structure에서 tree는
(1) cycle이 없고
(2) 방향성은 있다

그래서 위 그림에서 모양만 좀 바꾸면 B나 다른 애들이 root가 될 수도 있지 않나.. 라고 생각할 수 있는데, 단방향성을 가지기 때문에 안된다.
그런 이유도 있겠지만, 애초에 root node를 따로 정의하는게 tree이다.

5.1.2 Representation of Trees

5.1.2.1 List Representation

일반적인 linked list로 표현하면 이전에 만들어둔 함수를 사용할 수 있다.

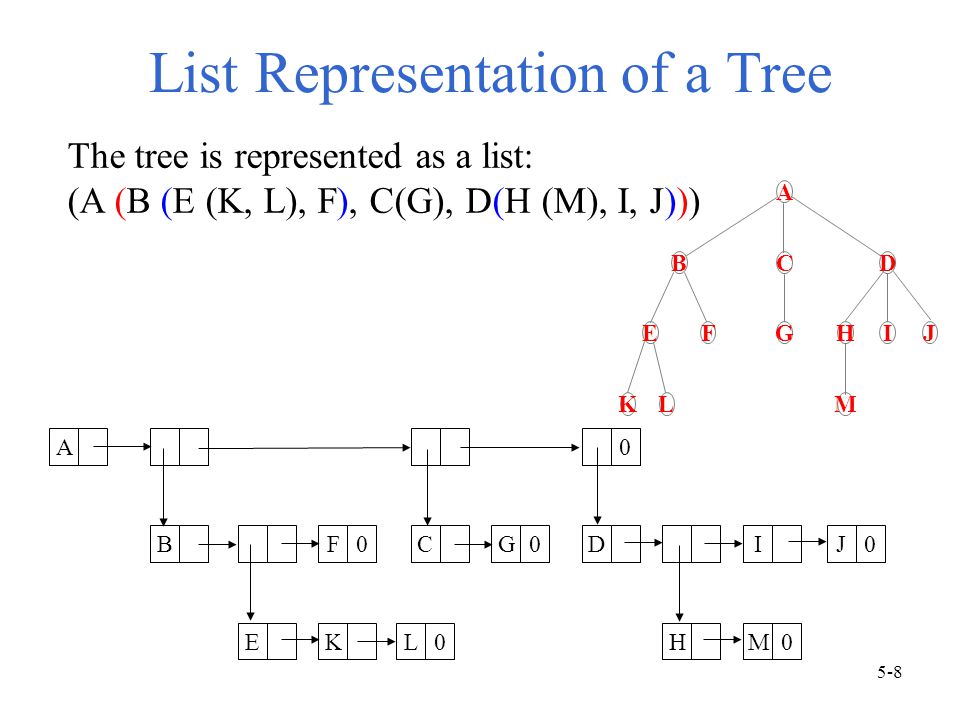
하지만 Tree에 최적화된 다른 표현법을 사용하는게 더 낫다.
근데 node별로 children 숫자가 다르기때문에 한 node가 가져야하는 link 수가 가변적이다.
그렇다고 제일 큰 수로 모두 통일해서 type을 만들어버리면 공간 낭비가 심하다.

5.1.2.2 Left Child-Right Sibling Representation

data와 left child, right sibling을 저장한다.(위 방식보단 간단하게 표현되고 좋은듯)
child 중 누가 left에 와도 딱히 상관없다.(밑에 subtree는 같이 와야지)

5.1.2.3 Representation as a Degree-Two Tree

Degree-Two Tree를 만드는 방법은
Left child-Right sibling Tree의 right sibling들을 모두 45도 시계방향으로 돌려버리면 된다.

바로 위 Tree를 Degree-Two Tree로 만들면,

이렇게 된다.
Left child-Right child로 나타낼 수 있다.
이를 Binary Tree라고 한다.

이렇게 변환된 Degree-Two Tree는 root의 right child가 없다.
right child가 있으려면 변환전 root에 right sibling이 있었어야하는데, 이는 불가능하다.

5.2 BINARY TREES

5.2.1 The Abstract Data Type

위 방법(left child-right sibling tree를 degree-two tree로 변환하는 방법)을 통해 우리는 어떤 Tree도 Binary Tree로 바꿀 수 있다.

Definition
: A binary tree is a finite set of nodes that is either empty or consists of a root and two disjoint binary trees called the left subtree and the right subtree.

ADT
Binary Tree ADT는 p.199

Tree와 차이
Binary Tree는 left tree와 right tree를 구분해야한다.
Empty Tree일 수도 있다.

한 root에 왼쪽 child만 있는 tree와 오른쪽 child만 있는 tree는 binary tree 관점에서 서로 다른 tree이다.
그냥 tree 관점에선 좀 다르게 그려진 같은 tree이다.(순서 상관 X)

Skewed Tree

한쪽으로 기울어진 binary tree

5.2.2 Properties of Binary Trees

Binary Tree에 대해 (root level 1부터 시작)

  1. level i의 최대 node 수는 2i−12^{i-1}이다. (i≥1i \geq 1)

  2. depth k인 경우 해당 binary tree의 최대 node 수는 2k−12^k-1이다. (k≥1k \geq 1)

  3. leaf node를 n0n_0, degree가 2인 node를 n2n_2라고 할때,
    n0=n2+1n_0 = n_2 + 1이다.

3번 증명
: n이 총 node 수이고 n_k이 degree가 k인 node 수라면,
(1)n=n0+n1+n2n=n_0+n_1+n_2이다.

root를 제외한 각 node는 하나의 Branch(B)에서 내려왔으므로
n=B+1n=B+1이다.(B는 root 제외한 node 수이니 +1 해준다.)

degree가 1인 node는 branch 1개, 2인 node는 2개 가지고 있으니,
(2)n=B+1=n1+2n2+1n=B+1=n_1+2n_2+1 이다.(degree는 밑으로 뻗는 가지만 생각하니까 겹칠 일 없음)

(1)과 (2)를 빼면 결과를 얻을 수 있다.

Full Binary Tree

Definition
: A full binary tree of depth k is a binary tree of depth k having 2k−12^k-1 nodes, k≥0k \geq 0

그냥 꽉찬 binary tree

어떤 level에서든 왼쪽에서 오른쪽으로 번호를 매긴다.(complete binary tree에서 이용가능)

Complete Binary Tree

Definition
: A binary tree with n nodes and depth k is complete iff its nodes correspond to the nodes numberd from 1 to n in the full binary tree of depth k.

즉, leaf가 왼쪽부터 순서대로 차있는 binary tree

위의 2번 공식을 활용해, nodes수가 n인 complete binary tree의 depth는
⌈log⁡2(n+1)⌉⌈\log_2{(n+1)⌉}이다. (⌈x⌉는 x보다 크거나 같은 정수 중 가장 작은 수, ceil function)

5.2.3 Binary Tree Representations

5.2.3.1. Array Representation

여기 숫자를 index로 생각하고 1차원 배열에 binary tree를 저장할 수 있다.(0 위치는 비워둠)

계산법 (complete binary tree이고, n개의 nodes가 있다고 가정)
(1≤i≤n)1\leq i\leq n)

  1. Parent(i): ⌊i/2⌋⌊i/2⌋이다. ii가 1이라면 이는 root이므로 parent 없다.
    (⌊x⌋는 floor function)

  2. LeftChild(i): 2i2i이다. 2i>n2i>n이면 left child는 존재하지 않는다.

  3. RightChild(i): 2i+12i+1이다. (2i+1)>n(2i+1)>n이면 right child는 존재하지 않는다.

꼭 complete binary tree가 아니어도 사용할 순 있다.
물론 child가 존재하지 않는 범위는 다시 설정해야되고,
**complete binary tree는 적합**하지만, **아닌 경우 array로 표현하면 공간이 심하게 낭비**될 수도 있긴하다.
(skewed의 경우 k 저장하는데 2^k-1 공간이 필요..)

Proof 2
귀납적으로 증명한다.(자세한건 p.202)
1의 left child가 2인건 분명하다.
j의 left child를 2j라고 한다면,
j+1의 left child 바로 전에 j의 left와 right child가 와야한다.
j+1의 left child는 2j+2이다.

5.2.3.2 Linked Representation

위 array 방식도 complete binary tree의 경우 쓸만하지만,
나머지 tree들을 표현하려면 공간이 낭비될 수 있고, insertion이나 deletion에 애로가 있다.
그래서 linked로 표현한다.

typedef node *treePointer;
typedef struct node {
	int data;
    treePointer leftChild, rightChild;
} node;

parent 정보가 필요하면 추가해주면 된다.
일단 이것만으로도 대부분 잘 작동한다.

root node를 가리키는 pointer를 통해 tree에 접근한다.

5.3 BINARY TREE TRAVERSALS

R : 오른쪽으로 이동
L : 왼족으로 이동
V : 해당 node visit (ex. print data field)
으로 하면, 총 6가지 traversal 조합이 나온다.
보통 오른쪽보다 왼쪽을 먼저가니 그 경우만 추리면
LVR, LRV, VLR 세가지 경우가 있다.
각각이 inorder, postorder, preorder이다.

5.3.1 Inorder Traversal

Inorder tarversal에서는
(1) 왼쪽으로 내려갈 수 없을때까지 내려간다.
(2) 해당 node를 visit하고,
(3) 오른쪽으로 한칸 내려간다.
(3)-1 오른쪽으로 내려갈 수 없으면 이전 node로 올라가고 visit한 후 오른쪽으로 한칸 내려간다.
(1)~(3)-1 과정을 반복한다.

void inorder(treePointer ptr) {
	if (ptr) {
    	inorder(ptr->leftChild);   //왼쪽 subtree에 대해 inorder 진행
        printf("%d ", ptr->data);  //visit
        inorder(ptr->rightChild);  //오른쪽 subtree에 대해 inorder 진행
    }
}

"visit" 순서 : 왼쪽 subtree 전체 -> root -> 오른쪽 subtree 전체
(모든 subtree에 대해 위 과정을 적용한다. 그룹화 시켜가며 방문 순서를 정한다.)

사용 예
BST(Binary Search Tree)에서 오름차순 또는 내림차순으로 값을 가져오기위해 주로 사용한다. 내림차순으로 가져오려면 역순으로 진행한다.

모든 node를 방문해야하니 총 node수가 recursion 함수가 "호출"되는 횟수이다.
leaf에 양쪽에 NULL node가 붙어있다고 생각해서 node 개수를 세면,
총 node 개수만큼 recursion 함수가 호출된다.(양쪽 NULL에도 가보기는 해야됨)

5.3.2 Preorder Traversal

Preorder Traversal에서는
(1) 해당 node를 visit하고 왼쪽으로 내려간다. 이 과정을 반복한다.
(2) 왼쪽으로 더 이상 내려갈 수 없으면, 오른쪽으로 한칸 내려간다.
(2)-1 오른쪽으로 내려갈 수 없으면, 오른쪽으로 내려갈 수 있을때까지 이전 node로 올라간다.
(1)~(2)-1 과정을 반복한다.

void preorder(treePointer ptr) {
	if (ptr) {
    	printf("%d ", ptr->data);   //visit
    	preorder(ptr->leftChild);   //왼쪽 subtree에 대해 preorder 진행
        preorder(ptr->rightChild);  //오른쪽 subtree에 대해 preorder 진행
    }
}

"visit" 순서 : root -> 왼쪽 subtree 전체 -> 오른쪽 subtree 전체
(모든 subtree에 대해 위 과정을 적용한다. 그룹화 시켜가며 방문 순서를 정한다.)

사용 예
prefix expression을 표현하는데 사용된다.

5.3.3 Postorder Traversal

Postorder Traversal에서는
(1) 왼쪽으로 내려갈 수 없을때까지 내려간다.
(2) 오른쪽으로 내려갈 수 없을때까지 내려간다.
(2)-1 오른쪽으로 내려갈 수 없으면, 일단 visit하고, 오른쪽으로 내려갈 수 있을 때까지 왔던 길을 다시 올라가며 visit한다.
(2)-2 그 후 다시 오른쪽으로 끝까지 내려간다.
(3) 오른쪽으로 끝까지 내려갔으면, 일단 visit하고, 올라왔던 길을 다시 올라가며 visit한다.
(1)~ 과정을 반복한다.

void postorder(treePointer ptr) {
	if (ptr) {
    	postorder(ptr->leftChild);   //왼쪽 subtree에 대해 postorder 진행
        postorder(ptr->rightChild);  //오른쪽 subtree에 대해 postorder 진행
        printf("%d ", ptr->data);    //visit
    }
}

"visit" 순서 : 왼쪽 subtree 전체 -> 오른쪽 subtree 전체 -> root
(모든 subtree에 대해 위 과정을 적용한다. 그룹화 시켜가며 방문 순서를 정한다.)

사용 예
Tree를 복사하거나 식 계산하는데 주로 사용된다.
복사할때 child를 먼저 복사해야 parent의 link값이 생기기 때문이다.
식 계산할때는 먼저 왼쪽 subtree와 오른쪽 subtree를 방문해야 해당 node의 값을 구할 수 있기 때문이다.(밑에 예시 있음)

5.3.4 Iterative Inorder Traversal

Traversal을 구현하는데, recursion말고 반복문을 이용할 수도 있다.
그러려면 stack을 이용해야한다.
visit이 unstack이고, 아무 action이 없다면 그저 stack에 쌓이는거다.
stack이 비면 끝난다.
system stack이 resursive function에 하듯이 하면된다.

void IterInorder(treePointer node) {
    while (1) {
    	while (node) {
    		push(node);
        	node = node->leftChild;
		}
        node = pop();
        if (!node) break;  //empty stack
        printf("%d ", node->data);  //visit
        node = node->rightChild;
	}
}

5.3.5 Level-Order Traversal

각 level마다 왼쪽에서 오른쪽으로 탐색한다.
Queue를 사용한다.

void levelOrder(treePointer ptr) {
	if (!ptr) return;  //emtpy tree

	addq(ptr);
	while (1) {
    	ptr = deleteq();
        
        if (!ptr) break;  //empty queue
        
        printf("%d ", ptr->data);
        
        if (ptr->leftChild)
        	addq(ptr->leftChild);
        if (ptr->rightChild)
        	addq(ptr->rightChild);
    }
}

Traversal without a Stack

Stack 없이 traversal이 가능한가?(recursion도 간접적으로 stack을 사용한걸로 생각하면(system stack))

1) parent node를 가리키는 link를 만들어주면, 이를 활용해서 할 수 있다.
2) Threaded binary tree를 사용한다. 5.5에 자세히 나오는데, 새로 공간을 추가하기엔 소모가 심해서 기존의 leftChild/rightChild field를 사용한다.

5.4 ADDITIONAL BINARY TREE OPERATIONS

위에서 배운 binary tree와 traversals를 사용해 operation 몇개를 구현할 수 있다.

5.4.1 Copying Binary Trees

Postorder traversal을 수정하여 만든다.

treePointer copy(treePointer original) {
	treePointer temp;
    if (original) {
    	MALLOC(temp, sizeof(*temp))
        temp->leftChild = copy(original->leftChild);
        temp->rightChild = copy(original->rightChild);
        temp->data = original->data;
        
        return temp;
    }
    return NULL;
}

5.4.2 Testing Equality

Preorder traversal을 수정하여 만들었다.

int equal(treePointer first, treePointer second){
    if (first == NULL && second == NULL)
    	return 1;  //leaf의 child에선 둘다 NULL일때 true 반환해줘야됨
    
    //둘 다 NULL이 아닌 경우, 본인들 data가 같고, 왼쪽 subtree와 오른쪽 subtree가 같아야 한다.
    return ((first->data == second->data)
    		&& equal(first->leftChild, second->leftChild)
    		&& equal(first->rightChild, second->rightChild));
}

이를 압축해서 적으면

int equal(treePointer first, treePointer second){
    return ((!first && !second)
    		|| (first && second
    		&& (first->data == second->data)
    		&& equal(first->leftChild, second->leftChild)
    		&& equal(first->rightChild, second->rightChild)));

위에서의 if문은 ||로 묶어줬다.
위에선 if문 들어가면 반환되기때문에 return 문에서 first && second인지, 즉 둘다 NULL이 아닌지 굳이 확인할 필요가 없었지만, 이 경우 확인해봐야돼서 추가해줬다.

5.4.3 The Satisfiability Problem

Propositional fomula라고하면 'x∪y∩~x' 처럼 proposition들로 구성된 식을 말한다.
Satisfiability Problem은 이 propositional calculus의 formula가 TRUE가 되도록하는 각 variables 값이 있는가 하는 것이다.

이를 확인하는 가장 확실한 방법은 모든 경우의 수를 찾아보는 것이다.
n개의 variable이 있다면, 2^n개의 가능한 조합이 있다.
(O(g2^n), g는 variable에 assign하고 계산하는 시간)

Tree에 이 formula가 저장돼있다고 하고 모든 경우의 수를 찾아 계산해보자.

계산

postorder traversal을 이용해야 한다.
postorder는 특정 node P에 visit하기전에 해당 node의 왼쪽과 오른쪽 node를 모두 traverse한다.
P의 값을 계산하려면 왼쪽 subtree와 오른쪽 subtree의 값을 알아야 하므로 postorder 방식을 사용해야한다.

각 node는 4개의 field를 갖는다. leftChild, rightChild, data, value
data는 기호나 값(true, false, and, or, not)을 저장하고, value는 계산 결과(TRUE, FALSE)를 저장한다.

typedef enum{not, and, or, true, false} logical;

void postOrderEval(treePointer node) {
	//계산결과를 root에 저장해준다. tree 만드는건 함수밖에서,,
    
    if (node) {
    	postOrderEval(ptr->leftChild);
        postOrderEval(ptr->rightChild);
        switch (node->data) {
        	case not:
            	node->value = !node->rightChild->value;
                break;
            case and:
            	node->value = node->rightChild->value && node->leftChild->value;
                break;
            case or:
            	node->value = node->rightChild->value || node->leftChild->value;
                break;
            case true:
            	node->value = TRUE;
                break;
            case false:
            	node->value = FALSE;
                break;
        }
    }
}

5.5 THREADED BINARY TREE

잘보면 일반적인 Tree들은 실제 값이 있는 link보다 NULL인 link가 더 많다. 정확히 2n개의 link 중 n+1개가 NULL link이다.

n1은 상쇄되니 고려하지 않고, n0 = n2 + 1 이다.
n0는 2개씩 NULL link가 있고, n2는 2개씩 실제 link가 있으니 NULLlink = REALlink + 1이다.
따라서 전체 link가 2n개 있으면 n-1개는 실제 link이고, n+1개는 NULL이다.

A.J. Perlis와 C. Thornton은 이 NULL link를 이용할 방법을 고완했다.
다른 node를 가리키는 포인터인 thread로 이를 활용한다.

  1. 특정 node ptr의 ptr->leftChild가 NULL이라면,
    inorder traversal을 했을때 ptr 이전에 visit한 node를 가리키게 한다.
    즉, ptr의 inorder predecessor을 가리킨다.
  2. 특정 node ptr의 ptr->rightChild가 NULL이라면,
    inorder traversal을 했을때 ptr 이후에 visit할 node를 가리키게 한다.
    즉, ptr의 inorder successor을 가리킨다.

표현할때 일반 Child와 Thread는 구분해줘야하는데,
보통 leftThread, rightThread fields를 추가한다.
해당 fields가 TRUE이면 Child에 있는게 Thread인거고, FALSE면 그냥 Child인거다.

값을 찾을 수 없는 thread가 있을 수 있다.(inorder predecessor나 successor가 없는 경우)
이런 경우를 막기위해 우리는 Threaded binary tree에 Header node를 추가한다.
기존 original tree의 root를 header node의 left Child로 연결시킨다.

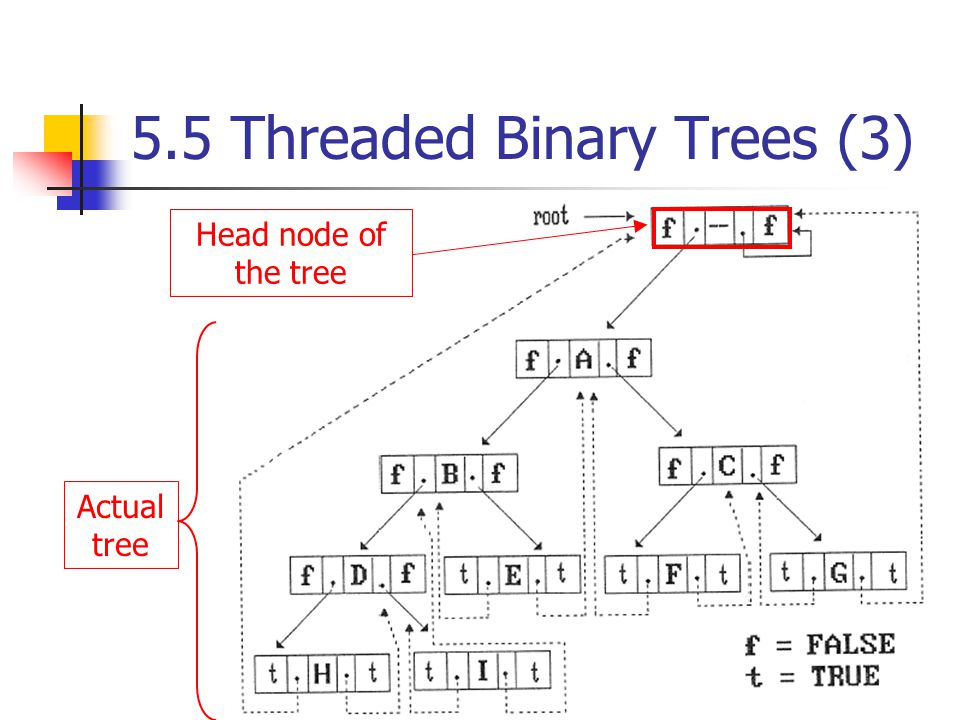
원래는 H node의 left child와 G node의 right child는 가리킬 곳이 없었는데 header node를 가리키도록 한다.
즉, 사실상 제일 처음 방문하는 node의 이전 node와, 제일 마지막 visit하는 node의 다음 node를 header node로 정해준 것이다.

Header node의 right Thread는 FALSE이고, 본인을 가리킨다.
Empty tree일 경우
Header node의 각 child는 본인을 가리키고,
leftThread는 TRUE, rightThread는 FALSE이다.

5.5.2 Inorder Traversal of a Threaded Binary Tree

Find Inorder Successor

우선, Threaded binary tree에서 특정 node의 successor을 찾아보자.(Threaded Binary Tree는 다 만들어져 있다고 가정)

  1. node ptr의 rightChild가 thread라면, rightChild가 inorder successor이다.

  2. node ptr의 rightChild가 thread가 아니라면(실제 node있단 소리), rightChild로 간 다음 해당 node로부터 leftThread가 TRUE일때까지 내려간다.(즉, leftChild로 끝까지 내려간다)
    해당 node가 inorder successor이다.

그대로 code로 표현하면..

threadedPointer insucc(threadedPointer ptr) {
	threadedPointer temp;
    temp = ptr->rightChild;
    if (!ptr->rightThread) { //thread가 맞으면 그냥 temp 반환하면됨
    	while(!temp->leftThread)
        	temp = temp->leftChild;
    }
    return temp;
}

Inorder Traversal without Using Stack

Thread를 이용해 우리는 stack없이 inorder traversal을 할 수 있다.
위의 successor을 찾는걸 반복하면 된다. 찾고 visit하고 찾고 visit하고...

void tinorder(threadPointer tree) {
	threadPointer temp = tree; //header node부터 시작해도 상관없다.
    for (;;) {
    	temp = insucc(temp);
        if (temp == tree) break;  //structure아니라 pointer니까 비교 가능
        printf("%d ", temp->data);
    }
}

5.3.3 Inserting a Node into a Threaded Binary Tree

node s 아래에 r을 넣는다고 했을때
(1) 오른쪽에 집어넣는 방법과
(2) 왼쪽에 집어넣는 방법이 있다.

1. 오른쪽에 집어넣기(s->rightChild)

(a) s의 right subtree가 empty일 경우,
s의 rightChild에 r이 오고,
r의 양쪽 link(Child)는 Thread가 되는데, leftChild는 s를 가리키고, rightChild는 s의 Thread 값을 이어받는다.
(s 다음에 visit할 node가 s->rightThread였는데, r이 s 다음에 visit할 node가 되어버렸으니 r에 해당 Thread 값을 넘겨준다.)

(b) s의 right subtree가 empty가 아닐 경우,
s의 rightChild에는 r이 오고,
r의 오른쪽 link(Child)는 해당 subtree의 root node를 가리킨다.
r의 왼쪽 link(Child)는 Thread가 되는데, s를 가리킨다.
r이 중간에 삽입되면 특정 node의 inorder predecessor이 된다.
s자리에 r이 오는 꼴이니, s의 inorder successor가 그 특정 node이다. 즉 s의 inorder successor를 찾아서 해당 node의 leftChild(Thread)를 r로 연결해주면 된다.

void insertRight(threadPointer s, threadPointer r) {
	threadPointer temp;
    
    //r의 오른쪽에 뭐가 오든 그냥 연결(Thread이든 Node이든)
	r->rightChild = s->rightChild;
    r->rightThread = s->rightThread;
    
    //r의 왼쪽(Thread)은 그 위 node 연결
    r->leftChild = s;
    r->leftChild = TRUE;
    
    //s 오른쪽에 r연결
    s->rightChild = r;
    s->rightThread = FALSE;
    
    //r의 오른쪽 subtree가 empty가 아니면 subtree의 Thread값 변경
    if (!r->rightThread) {
    	temp = insucc(r);  //r을 연결했으니 r의 inorderSuccessor구한다.
        temp->leftChild = r;
    }
}

2. 왼쪽에 집어넣기(s->leftChild)

(a) s의 left subtree가 empty일 경우,
s의 leftChild에 r이 오고,
r의 양쪽 link(Child)는 Thread가 되는데, leftChild는 s의 Thread 값을 이어받고, rightChild는 s를 가리킨다.

(b) s의 left subtree가 empty가 아닐 경우,
s의 rightChild에는 r이 오고,
r의 왼쪽 link(Child)는 해당 subtree의 root node를 가리킨다.
r의 오른쪽 link(Child)는 Thread가 되는데, s를 가리킨다.
r이 중간에 삽입되면 특정 node의 inorder successor이 된다.
즉, s의 predecessor을 일단 구해야 하는데, predec 함수를 따로 만들어서 해주면 될 것 같다.
s(or r)의 predecessor을 찾아준 후 해당 node의 rightChild(Thread)가 r을 가리키게 해준다.(s자리에 r이 들어온 셈)

void insertleft(threadPointer s, threadPointer r) {
	threadPointer temp;
    
    //r의 왼쪽에 뭐가 오든 그냥 연결(Thread이든 Node이든)
	r->leftChild = s->leftChild;
    r->leftThread = s->leftThread;
    
    //r의 오른쪽(Thread)은 그 위 node 연결
    r->rightChild = s;
    r->rightChild = TRUE;
    
    //s 왼쪽에 r연결
    s->lefttChild = r;
    s->leftThread = FALSE;
    
    //r의 왼쪽 subtree가 empty가 아니면 subtree의 Thread값 변경
    if (!r->leftThread) {
    	temp = predec(r);
        temp->rightChild = r;
    }
}
<<predec 함수>>

node A의 predecessor를 찾아보자.

A의 leftChild가 Thread라면 그 자체로 predecessor가 된다.

Thread가 아니라면, 직접 찾아야된다.
root A의 왼쪽 subtree에 마지막으로방문한 node가 있다.
inorder 자체가 왼쪽을 다 돌고 root node인 A에 오기 때문이다.
따라서 일단 A의 left child인 AL node로 가준다.

node AL을 root로 하는 tree에서, 오른쪽 subtree에서 마자막으로 방문한 node가 predecessor이다.
왜냐하면 한번 더 말하지만,
inorder 자체가 왼쪽 subtree먼저 다 돌고 root(AL) visit하고 오른쪽 node돌기 때문이다.

즉, A의 입장에선 AL이 root인 tree의 오른쪽 subtree에 마지막으로 방문한 node가 있다.
이렇게 계속 오른쪽 subtree로 쭉 내려간다.
내려가다가, 특정 root를 기준으로 right subtree가 없고, left subtree만 있다면,
그 root node가 마지막으로 방문한 node, 즉 우리가 찾는 predecessor이다.
(왼쪽 subtree 돌고 root 가기 때문에 왼쪽 subtree보단 root가 나중이다.)

즉, insucc에서와 비슷하게 왼쪽으로 한칸 간 후, 오른쪽으로 끝까지 내려가보면 predecessor이 있다.
(insucc에선 오른쪽으로 한번 갔다가 왼쪽으로 끝까지 내려감, insucc도 이런 식으로 이해할 수 있다.)

code..는 insucc 좀만 수정하면 금방 짜니까 생략

5.6 HEAPS

Heap을 활용해 주로 Priority Queue를 구현한다.
(MaxPriorityQueue의 ADT는 p.223)

5.6.1 Priority Queues

Priority Queue 예시
: 특정 machine을 여러 user가 사용한다고 해보자, user마다 사용 시간이 다르다면 시간이 적게 걸리는 사람부터 처리할 수 있다. 이 경우 Min Priority Queue가 필요하다.

Priority Queue를 (1)연속적인 데이터나 chain으로 나타낼 수도 있고, (2)Heap으로도 나타낼 수 있는데,
후자의 경우가 여러 operation에서 시간이 적게 걸린다.

5.6.2 Definition of Max Heap

Max Heap은 Complete Binary Tree의 한 종류이다.

Definition
: A max(min) Tree는 각 node의 key value가 본인의 children들보다 작지(크지) 않은 tree이다.
A max(min) Heap은 Complete Binary Tree이면서 max(min) Tree인 경우이다.

쉽게 말해 max heap은 complete binary tree이면서 root로 갈수록 커져야되고,
min heap은 반대이다.
max heap은 root값이 가장 크고, min heap은 root값이 가장 작다.

5.6.3 Insertion into a Max Heap

Max Heap에 삽입할때, Complete Binary Tree가 돼야 하므로 아무데나 삽입할 수 있는게 아니라 한군데(제일 끝)밖에 못한다.
그 한곳에 삽입하는데 parent의 key value가 더 작다면, 둘의 위치를 바꾼다. 해당 과정을 parent의 key value가 삽입할 node의 key value보다 클때까지 진행한다.(최소 횟수로 반복)

Complete Binary Tree는 (chain으로 표현할 수도 있지만) Array로도 잘 표현되니 Array로 표현해보자.(0 위치는 비워둔다)
(dynamically allocated array로 표현할 수도 있다. 가변길이로.)

#define MAX_ELEMENTS 200 //maximum heap size+1

#define HEAP_FULL(n) ((n) == MAX_ELEMENTS - 1)
#define HEAP_EMPTY(n) (!(n))

typedef struct {
	int key;
    //추가 값
} element;
element heap[MAX_ELEMENTS];
int n = 0;
void push(element item, int *n) {
	int i;
    if (HEAP_FULL(n)) {
    	fprintf(stderr, "The heap is full.\n");
        exit(EXIT_FAILURE);
    }
    i = ++(*n);
    while (i != 1 && heap[i].key > heap[i/2].key) {
    	heap[i] = heap[i/2];
        i /= 2;
    }
    heap[i] = item;
}

Analysis (push)
: 한 level씩 올라간다. n개의 node가 있다면 O(log⁡2n)O(\log_2n) time complexity를 가진다.

5.6.4 Deletion from a Max Heap

Max Heap에서 delete 한다는 것은 root를 꺼내는 것이다.

(1) root node를 꺼내오고 나면, 한자리가 빈다. complete binary tree여야하므로 마지막 자리 node(A)를 빼버린다.
(2) A의 값과 root의 children들을 비교해 가장 큰 값을 root자리에 넣는다.
(3) 2번의 과정을 root부터 쭉 내려가며 반복한다. A가 들어갈 자리가 생기면 끝난다.

element pop(int *n) {
	int parent child;
    element item, temp;
    if (HEAP_EMPTY(n)) {
    	fpritnf(stderr, "The heap is empty.\n");
        exit(EXIT_FAILRUE);
    }
    
    itemp = heap[1];
    
    temp = heap[(*n)]; n--;
    parent = 1;
    child = 2;
    while (child <= (*n)) {
    	if (child < (*n))  //child 중 더 큰놈으로 보자
        	heap[child].key > heap[child+1].key ? 1 : child ++;
            
        if (heap[child].key < temp.key)
        	break;  //들어갈 자리 찾으면 break
        
        heap[parent] = heap[children];
        parent = children;
        children *= 2;
    }
    heap[parent].key = temp.key;
    return item;
}

Analysis (pop)
height이 ⌈log⁡2(n+1)⌉⌈\log_2(n+1)⌉ 이므로,
push와 마찬가지로 O(log⁡2n)O(\log_2n)이다.

5.7 BINARY SEARCH TREES

Dictionary 는 pair의 collection이다. pair는 key와 그에 해당되는 data의 조합이다.
이를 BST를 이용해 나타내보자.
Dictionary ADT는 p.231

5.7.1 Definition

Binary Search Tree(BST)는 이전의 어떤 data structures보다 퍼포먼스가 좋다.
key 값과 rank 둘 다로 작동할 수 있다.(ex. 50번째 작은 수 삭제, key값 3 찾기)

Definition
: A Binary Search Tree(BST) is a binary tree. It may be empty. If it is not empty then it satisfies the following properties
(1) 각 node는 1개의 key만을 가지고 중복이 없다.
(2) left subtree의 key들은 root의 key보다 작다.
(3) right subtree의 key들은 root의 key보다 크다.
(4) left/right subtree 또한 BST이다.

Representation
array 표현은 거의 complete binary tree에서만 가능하므로, BST가 balanced가 아닌 경우 link로 표현해주는게 맞다.

5.7.2 Searching a Binary Search Tree

root부터 recursive로 비교해나간다.
물론 iterative 버전으로도 만들 수 있다.(끝까지 가면==NULL까지가면 실패)
처음부터 root가 NULL이면 실패.

code 생략.(p.233)

두 code다 BST의 높이를 h라고 했을때, O(h)이지만, recursive 버전은 O(h)의 stack 공간이 추가로 필요하다.(system stack)

5.7.3 Inserting into a Binary Search Tree

dictionary pair을 insert하려면, 우선 해당 key값이 존재하는지 확인해야 한다.

그래서 먼저 검색을해서 해당 key가 없는지 확인하고, Insertion을 진행한다.
마지막으로 검색을 진행한 node를 기준으로 좌or우 children에 insert한다.

위의 search 함수를 마지막으로 검사한 node를 반환하게 약간 수정하고, 이를 이용해 insertion을 진행한다.
Insert할 pair를 입력받아 MALLOC으로 node를 만들어주고, insert해주면 된다.

자세한 code 생략(p.235)
O(h)
NULL tree인 경우 삽입하는 경우도 생각해야됨.

5.7.4 Deletion from a Binary Search Tree

leaf node이거나,
non-leaf여도 one child인 경우는 삭제하기 쉽다.
해당 node free해주고, link 수정해주고, 후자의 경우 사라진 자리에 하나뿐인 child가 들어오면 된다.

부모랑 크기비교해서 옆으로 보내야 될 수도 되지않나? 라고 생각할 수 있는데 잘 생각해보면 아니다.
애초에 그 ancestors보다 작거나 커서 그 위치에 있는거다.

non-leaf이면서 two children인 경우,
deleted node를 기준으로 왼쪽 subtree에서 가장 큰 값 혹은 오른쪽 subtree에서 가장 작은 값이 빈 자리로 와야한다.
parent가 되려면 왼쪽 subtree 값들보단 커야하고, 오른쪽 subtree 값들보단 작아야하니 당연하다.

주의
왼쪽 subtree 가장 큰 node과 오른쪽 subtree 가장 작은 node의 degree는 최대 1이다.
그래서 빈자리로 가져온 값은 one child일 경우 아래의 child가 채우고, leaf node일 경우 그냥 사라진다..

마찬가지로 O(h)

5.7.5 Joining and Splitting Binary Trees

PASS
(읽어보긴 했는데, 일단 이런게 있다 정도만 알고가도 될듯. 딱히 필요성을 못느끼겠네, 내가 필요성을 판단해도 될진 모르지만...)

5.7.6 Height of a Binary Search Tree

최악의 경우라면, 예를들어 insertion 함수를 통해 빈 tree에 1,2,3...,n을 넣으면, 높이는 n이 된다.
이런 경우를 막기 위해, worst case에서도 O(log⁡n)O(\log n)의 height이 나오도록 제약하는 tree를 balanced search trees이다.
이 tree를 만드는 algrithm으론 AVL, red/black, 2-3, ... 등이 있는데 Chapter 10/11에서 다룬다.

5.8 SELECTION TREES

5.8.1 Introduction

k개의 정렬된 sequence가 있다고 해보자.
각 sequence에 data가 제각각 들어있는데 총 n개라고 해보자.
모든 sequence를 정렬되게 합치려면, 각 sequence의 최솟값을 비교해 가장 작은 값을 하나씩 빼오면 된다.
즉, 한번의 data 추출마다,k개의 data를 비교해야되니, k-1번의 비교가 필요하다.

k>2이면, 우리는 Selection Trees를 이용해 이 비교횟수를 줄일 수 있다.
(쉽게 말해서 토너먼트 형식으로 비교해서 비교 횟수를 줄임)

Selection Trees의 두 종류
1. Winner trees
2. Loser trees

heap은 n-1번 비교해야하지만 selection tree는 한번 구성해두면 그 다음부턴 훨씬 적은 비교로 최소(최대)값을 가져올 수 있다.
external sorting에서도 쓰인다.

5.8.2 Winner Trees

두 children 중 작은 값을 parent가 나타내는 complete binary Tree이다.
(minimum heap과 비슷하긴한데 다름)
(토너먼트 생각하면 됨)

구현은 Array로 한다.
(chain으로 하고 postorder로 계산하는것도 생각해봤는데 array에 비해 복잡하긴하네)

  1. leaf node부터 시작해서 토너먼트하듯이 올라간다.
  2. 그렇게 값을 하나 추출하고, 추출된 위치의 sequence만 새로운 값으로 대체하고 다시 계산한다.

합쳐져야 하는 data 개수가 많으므로, tree의 각 node는 각 sequence로의 pointer만 표시하게 한다.
각 node는 sequence의 p번째 값을 가리키면 된다.
(sequence를 다 가지고다니지 말라는 의미인듯)

5.8.3 Loser Trees

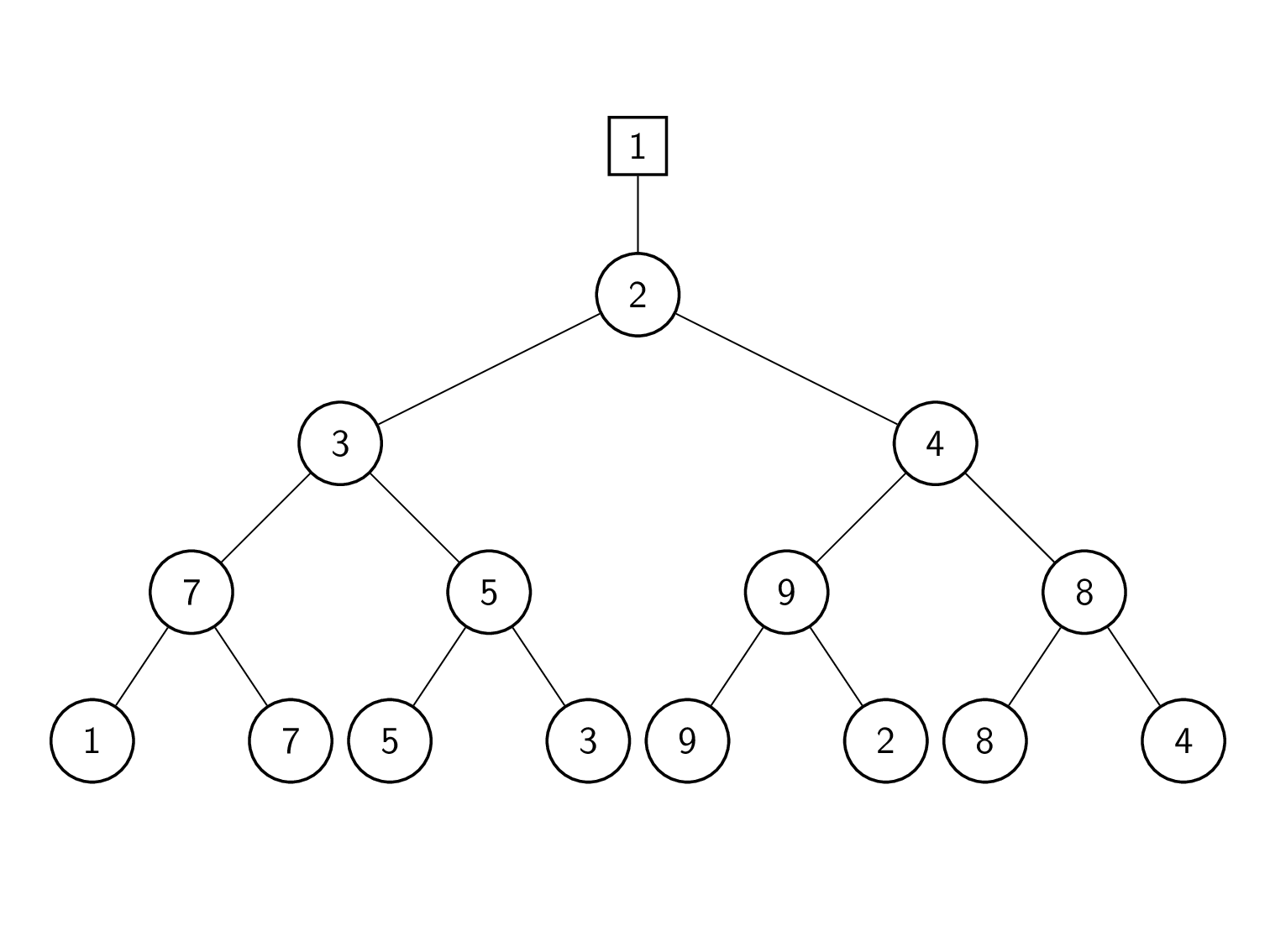
Winner Tree를 좀 더 간단하게 했다.(직관적으로 간단하진 않지만)
sibling과 비교해 패배한 node를 작성한다.
주의할 점은, 패배한 node를 작성하더라도 실제로 올라가는건 승리한 node이다.(위 그림 참고)

Advantage
winner tree에선 sibling과 비교하고 해당 path의 값들을 모두 수정해야했지만,
loser tree는 root까지 가는 길로의 parent하고만 비교하면 되고, 값을 수정하지 않을 수도 있다.

참고
external sorting시, heap, winner tree보다 loser tree를 주로 사용하는 이유
(내리다보면 "Why does external sorting often use loser tree"라고 있음)

5.9 FORESTS

Definition
: A forest is a set of n≥0n \geq 0 disjoint trees

트리가 여러개 분리돼있으면 그걸 forest라고 함.

5.9.1 Transforming a Forest into a Binary Tree

  1. 각 Trees를 Degree-two tree로 변환한다.
  2. 변환하면 rightChild가 없으니, root의 rightChild를 활용해 Tree들을 연결해준다.

5.9.2 Forest Traversals

forest F의 trees T에 대해,
T에 preorder traversal은 F에 forest preorder을 하는 것과 같다.

Forest preorder
1. F가 empty면 return
2. F의 첫번째 tree의 root visit
3. 첫번째 tree의 subtree에 대해 forest preorder 진행
4. F의 남은 tree도 forest preorder 진행

Forest inorder
1. F가 empty면 return
2. F의 첫번째 tree의 subtree에 대해 forest inorder 진행
3. 첫번째 tree의 root visit
4. F의 남은 tree도 forest inorder 진행

Forest postoreder
1. F가 empty면 return
2. F의 첫번째 tree의 subtree에 대해 forest postorder 진행
3. F의 남은 tree도 forest postorder 진행
4. 첫번째 tree의 root visit

level-order traversal of a forest는 forest버전과 binary tree버전의 결과가 다를 수 있다.

5.10 REPRESENTATION OF DISJOINT SET

5.10.1 Introduction

tree를 이용해 set을 표현하는 방법을 알아보자.

편의를 위해 각 set의 원소는 숫자로 나타내고, 같은 숫자(원소)를 포함하지 않는 sets은 disjoint set이다.
각 node는, set operation의 편의를 위해, children->parent로의 link를 가진다.


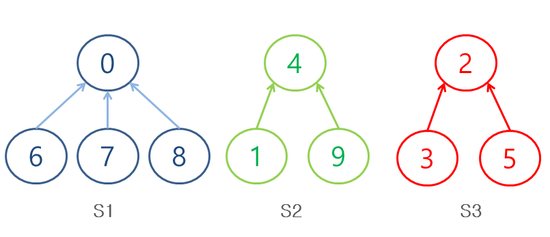
(S1 = {0,6,7,8}, S2 = {1,4,9}, S3 = {2,3,5} 인 예시)

Set Operations
1. Union : 합집합
2. Find : 특정 element를 포함하는 set을 찾는다.

두개의 operation에 대해 알아볼 것이다.

5.10.2 Union And Find Operations

(set을 tree로 나타냈으니)
S1∪S2는 하나의 tree를 다른 tree의 subtree로 만들면 된다.
간단하게, S2 root의 parent field를 S1 root를 가리키게 한다.(반대도 OK)

각 tree마다 set name을 연결해두기보단, 간단하게 각 tree의 root로 set을 구분한다.
즉, parent link를 통해 root까지 가면 어떤 set에 속해있는지 알 수 있다.

set name을 알고 싶으면 그냥 name[] 배열에 저장해두고,
root를 통해(혹은 root에 저장된 특정 정보를 통해) set name에 접근하면 된다.

Representation
Array로 표현한다.(parent)
각 node는 0 ~ n-1의 숫자값이기 때문에 array의 index로도 쓰일 수 있다.
그러면 이제 각 node의 parent link(index)만 저장하면 된다.
예시)

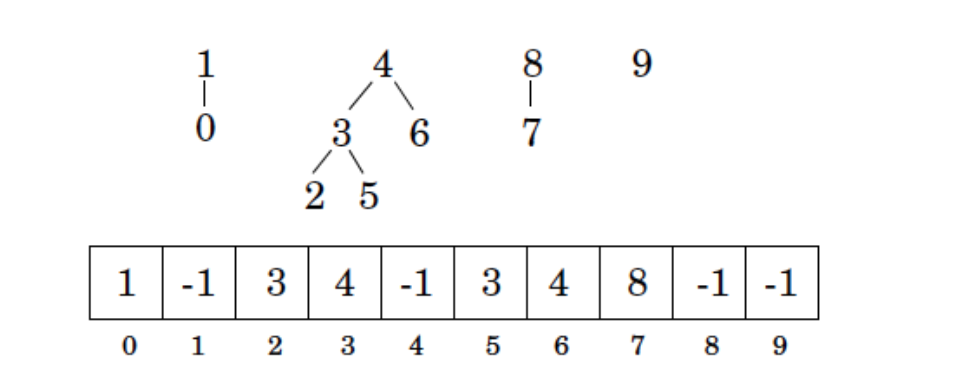
(-1은 root node를 나타냄)

Union & Find (simple)

int simpleFind(int i) {  //i를 포함하는 set 찾기
	while (parent[i] > -1)
    	i = parent[i];
    return i;
}

void simpleUnion(int i, int j) {  //i와 j는 root node여야함.
	parent[i] = j;
}

Analysis (simpleUnion & simpleFind)
구현하긴 쉽지만, performance는 그닥이다.
예를들어, 0 ~ (p-1)의 숫자가 각각 set을 나타낸다고 해보자.
이제 얘네에 대해
union(0,1), find(0)
union(1,2), find(0)
...
union(p-2,p-1), find(0)
를 하게되면, tree가 마치 skewed tree처럼 아래로 쭉 늘어진 모양이 된다.(degenerate tree)

이렇게 union하는데 총 걸리는 시간은 O(p)이다.
find를 하는데는 시작한 node의 level만큼 시간이 걸리므로, 위 operations에 걸리는 총 시간은 ∑i=2pi\sum_{i=2}^p i이다. 즉, O(p^2)이다.

다른 union 방법을 사용하면 degenerate tree가 만들어지는걸 막을 수 있고,
find를 더 빠르게 할 수 있다.

Weighting rule for union(i,j)

Definition
: tree i의 node 수가 tree j의 node 수보다 작다면, j를 i의 parent가 되게 한다.
(즉, 많은 놈 밑으로 적은 놈이 들어간다. 무식하게 그냥 붙이는게 아니라)

이 방식을 사용하면 위의 연산에서도 쭉 늘어진 degenerate tree가 아니라

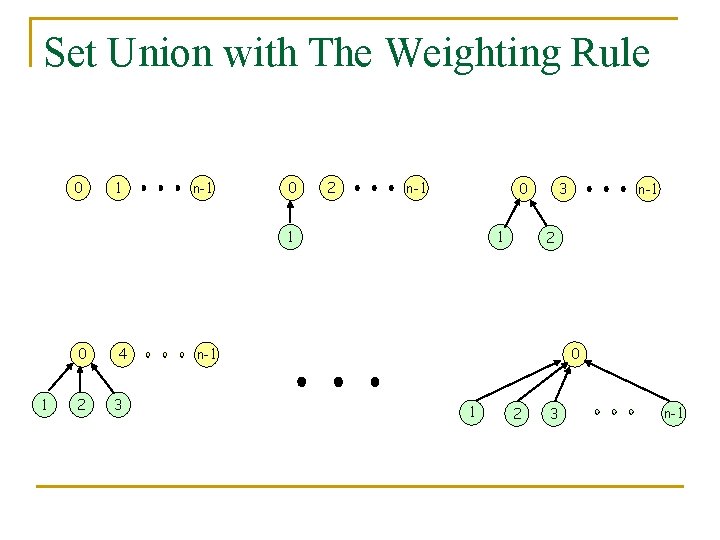
이런 모양의 tree가 나온다.

구현
node 수는 진행하며 계속 센다.(union할때 늘리는 식으로 계속 세나가면 될듯)
root node가 -1 값을 쓰고 있으니, 이 공간을 활용해 여기에 음수값으로 node수를 넣어준다.(ex. node 5개면 -5)

void weightedUnion(int i, int j) {  //i와 j는 root여야한다.
	int nodeCount = parent[i] - parent[j];
    
    if (parent[i] > parent[j]) {  //음수이므로 j의 node 수가 더 많다.
    	parent[i] = j;    		  //i의 parent를 j로..
        parent[j] = nodeCount;    //node 수 update
    }
    else {
    	parent[j] = i;
        parent[i] = nodeCount;
    }
}

Lemma 5.5 (위 방법 쓰면 level이 잘 제한되는지 알아보자)
: weightedUnion을 통해 만들어진 tree T의 node 개수가 n이라면, T의 level은 floor(log⁡2n)+1floor(\log_2n) +1 이하이다.
Proof
: n = 1일땐 맞다. 이제 i가 n-1일때 맞다고 가정하고, i가 n일때도 옳은지 증명해보자.
마자막으로 수행한 union(j,k)에서 j의 node 개수를 m이라고 해보자. 그럼 k의 node 개수는 당연히 n-m이다.
1≤m≤n/21\leq m\leq n/2라고 해보자.(반대로 n-m의 개수를 더 작은 걸로 잡아도 됨)
T의 최대 level은 k와 같거나, j의 level+1 이다.
(k의 level이 더 크다면 k와 같을 것이고, j의 level이 더 크다면 j가 k의 root에 붙으니까 j의 level+1이 될 것이다.)
이를 부등식으로 표현하면,
1) T′s max level≤⌊log⁡2(n−m)⌋+1≤⌊log⁡2n⌋+1T's\ max\ level \leq ⌊\log_2{(n-m)}⌋+1 \leq ⌊\log_2{n}⌋+1
2) T′s max level≤⌊log⁡2m⌋+1+1≤⌊log⁡2n/2⌋+2≤⌊log⁡2n⌋+1T's\ max\ level \leq ⌊\log_2{m}⌋+1+1 \leq ⌊\log_2{n/2}⌋+2 \leq ⌊\log_2{n}⌋+1

Collapsing rule for find(i)

Definition
: i에서 root로 가는 길에 j라는 node가 있다면(parent[i] != root(i)), parent[j]를 root(i)로 바꿔라.
(쉽게말해, root 찾으러 올라가는 길의 모든 node를 root와 직접 연결하란 소리.. 그럼 빨리 찾음)

//set을 찾고 나서 resetting
void collapsingFind(int i) {
	int root, trail, lead;
    
    for (root = i; parent[root] >= 0; root = parent[root]) ;
    
    for (trail = i; trail != root; trail = lead) {  //resetting
    	lead = parent[trail];
        parent[trail] = root;
    }
    return root;
}

Leamma 5.6
: 핵심은 이렇게 수정된 함수들 사용하면 worst case에서도 시간이 확실히 줄어든다는 것.(자세한 식은.. p.255)
분석은 p.253 제일 아래 부터

검색하다가 찾았는데 원본은 볼 엄두도 안나네

결국 union-find 위처럼 최적화하면 상수함수 급의 amortized time complexity 가진단 뜻인듯.(엄~청 천천히 증가하는 α\alpha 함수 사용했으니.. time complexity 분석할때 log 쓰는 것처럼 그냥 저 함수로 분석하는 거임)

그나마 이건볼만함.(아커만 함수로 증명하는건 아니긴함)

5.10.3 Application to Equivalence Classes

linked list의 배열로 하나하나 따라가면서 구했었는데,
그냥 같은 equivalence class는 union해버리면서 구할 수 도 있네.
union해버리고, element 하나씩 find하며 같은 equivalence class인지 확인할 수 있다.

PASS.

5.11 COUNTING BINARY TREES

nn개의 node를 가지는 distinct binary tree가 몇개인지 한번 세보자.
우선 전혀 다르지만 solution은 같은 3개의 문제에 대해 알아보자.

5.11.1 Distinct Binary Trees

특정 node 수로 만들 수 있는 구분되는 tree의 개수를 알아보자.

node의 개수 n이 0 or 1개라면 Distinct Binary Trees는 1개밖에 없다.
하지만 2라면 2개이고(leftChild와 rightChild는 구분됨),
3이라면 5개이다.

5.11.2 Stack Permutations

모든 binary tree는 unique한 preorder/inorder traversal pair를 갖는다.

preorder traversal의 결과를 통해 해당 tree의 root를 알 수 있고,
inorder traversal의 결과를 통해 root를 기준으로 left/right subtree를 구분할 수 있다.
이 과정을 반복해서 얻는 tree 모양은 하나 뿐이다.

예시로, 특정 tree T의 preorder 결과가 ABCDEFGHI이고 inorder의 결과가 BCAEDGHFI인 경우,
tree의 모양을 찾는 과정이 p.259~p.260에 있다.(마찬가지로 하나뿐)

Node가 n개일때 구분되는 tree의 개수

어떤 tree의 preorder sequence 결과에 따라 각 node에 숫자를 1~n까지 지정해주자.
preorder sequnce의 결과는 다음과 같을 것이다
: 1, 2, 3, ..., n

이 tree에 inorder traversal을 했을때 특정 결과, 예를들어 2,3,5,...,9,가 나온다면,
이 preorder/inorder 조합(1, 2, 3, ..., n/2,3,5,...,9)은 하나의 tree를 나타낸다.
즉, 나올 수 있는 inorder sequence 조합의 개수가 tree의 개수가 된다.

preorder/inorder/postorder 할때 stack을 사용해야했으니(특수한 경우 제외),
1~n 순서대로 stack에 넣고 빼며 만들어낼 수 있는 조합의 수가 tree의 개수가 된다.

5.11.3 Matrix Multiplication

(굳이 matrix가 아니어도 될 것 같긴한데)
M1*M2*M3 를 계산하는 순서의 경우의 수는 2가지이다.
matrices의 개수를 n이라고 할때, n=4이면 5가지이다.

M1n=M1×M2×...×MnM_{1n} = M_1×M_2×...×M_n 이라면,
M1n=M1i×Mi+1,nM_{1n} = M_{1i}×M_{i+1,n} 이다.

matrices개수가 n일때 경우의 수를 bnb_n이라고 하면
bn=∑i=1n−1bibn−i, n>1b_n=\sum_{i=1}^{n-1}b_ib_{n-i},\ n>1
이다.

bnb_n을 n개 node의 distinct binary tree 개수로 보자.
root node 양쪽에 subtree가 있는 모양이, 괄호로 나뉘어진 위 곱셈식과 비슷하다.
이에 맞게 좀 수정을 하면,
bn=∑i=0n−1bibn−i−1, b0=1b_n=\sum_{i=0}^{n-1}b_ib_{n-i-1},\ b_0=1

5.11.4 Number of Distinct Binary Trees

위에서 살펴본 세 풀이 모두 같은 결과를 말해준다.
이제 확실한 식을 구해보자.

바로 위 bnb_n 식의 recurrence를 풀어내야하다.

풀이과정 요약 많이 된 느낌이라 찾아보니
카탈랑 수
이거네그냥. 여기서 C를 B로 보자.

결론, bn=1n+1(2nn)b_n = \frac{1}{n+1} \begin{pmatrix}2n\\n\\ \end{pmatrix}

5.12 REFERENCES AND SELECTED READINGS

Tree 더 알고 싶다면,
The Art of Computer Programming (D.knuth)
Handbook of data structures and applications (D. Mehta, ...)

profile
지환
이전 포스트

Chapter 4. Linked Lists

다음 포스트

Chapter 6. GRAPHS

0개의 댓글