Chapter 6. GRAPHS

지환·2022년 4월 16일

6.1 THE GRAPH ABSTRACT DATA TYPE

6.1.1 Introduction

최초로 graph가 사용된 기록은 오일러(Leonhard Euler)가 Konigsberg bridge probelm을 풀때 사용한 것이다.

"이 다리들을 정확히 한번씩만 건너고, 출발했던 자리(A,B,C,D)로 돌아올 수 있는가"였는데,
오일러는 Graph를 이용해 땅은 vertex로 다리는 edge로 표현했다.
그리고 각 vertex의 degree가 짝수여야만 "한번씩만 건너고 원래 위치로 돌아오는 것"이 가능하다고 증명했는데,
위 graph에선 4개의 vertices가 모두 홀수 degree여서 불가능하다.

graph는 이후 electrical circuits 분석, shortest routes 찾기, cybernetics, linguistics 등등 다양한 곳에서 사용됐다.

6.1.2 Definitions

graph G는 V와 E 두개의 sets으로 구성된다.
V는 vertices의 finite nonempty set이다.
E는 pair of vertices(edges)의 set이다.
V(G)와 E(G)는 각각 graph G의 vertices와 edges의 set을 나타낸다.
G = (V,E)라고 그냥 graph를 나타낼때 사용하기도 한다.

undirected graph와 directed graph가 있다.(이 책에선 각각 graph와 digraph라고 부름)
전자의 경우 edge를 나타내는 (i,j)에 방향성이 없기 때문에 (i,j)나 (j,i)나 같은 edge를 나타낸다.
하지만 후자의 경우 <i,j>(i를 tail, j를 head라고 함)와 <j,i>는 다르다.
(이 책은 ()와 <>로 방향성이 있는지 구분하겠다고 함)

ex)

V(G) = {1, 2, 3, 4, 5, 6}
E(G) = {(1,2), (2,3), (3,4), (4,5), (4,6), (1,5), (2,5)}

Restrictions
1. 특정 vertex에 대해, 본인을 다시 가리키는 edge는 illegal이다.
이는 graph with self edges라고 따로 있는 data object이다.(일반 graph에선 다루지 않겠단 뜻)
2. 하나의 edge가 있는데, 다시 같은 edge가 존재할 순 없다.
directed일 경우 반대방향은 있을 수 있지만, 마찬가지로 같은 방향으로 같은 edge는 illegeal이다.
이런 경우 또한 multigraph라는 다른 data object이다.

Properties & Terminology

undirected graph에서의 vertex 수가 n개라고 할때, edge의 수는 최대 $\frac {n(n-1)} {2}$ 개 이다.
directed graph에선 최대 edge 수는 $n(n-1)$ 개 이다.
이렇게 최대 edge를 가지는 경우 complete graph라고 한다.

undirected graph에서 두 vertices가 edge (u,v)로 연결돼있다면,
이 두 vertices u와 v는 adjacent하다고 한다.
그리고 edge (u,v)는 vertex u와 v의 incident라고 한다.(한글로 잘 표현하기 어렵네 그냥 용어 익힐겸 적어는두자)

directed graph에서 두 vertices가 edge <u,v>로 연결돼있다면,
u is adjacent to v, v is adjacent from u 라고 한다.
그리고 edge <u,v>는 vertex u와 v의 incident라고 한다.

G에 대해 V(G') ⊆ V(G)이고, E(G') ⊆ E(G)인 graph G'을 G의 subgraph 라고 한다.
V와 E는 집합이니, 둘다 부분집합이면 subgraph란 뜻이다.
(vertex가 띄엄띄엄 있으면 그림은 subgraph처럼 안보일수도 있으니 정의대로 잘 판단하자.)

u에서 v까지의 path란, u에서 v까지 edges를 통해 나가는 길이다. 보통 vetices의 sequnce로 나타낸다. u,i1,i2,...,ik,v (edges의 sequence로 나타낼 수도 있다.)
simple path란, path에서 모든 vertex가 구분되는 경우를 말한다. 단, 처음 vertex와 마지막 vertex는 같을 수도 있다.
legngth란, path의 edges 개수이다.

cycle이란, simple path이면서 처음과 마지막 vertex가 같은 경우이다.

> undirected graph <
undirected graph G내의 두 vertex u와 v 사이에 path가 있다면, 그 두 vertex는 connected. (역도 성립)
undirected graph G의 모든 distinct vertices에 대해 서로간에 path가 있다면, 그 graph는 connected. (역도 성립)

undirected graph의 connected component(component)는 maximal connected subgraph이다.
maximal이란 말은 해당 subgraph를 포함하는 또다른 connected subgraph가 없단 소리다.
(쉽게말해서 graph내에서 연결되지 않고 분리된 덩어리를 connected commponent(or just 'component')라고 한다.)
tree는 connected acycle(no cycle) graph이다.

> directed graph <
directed graph G는 strongly connected이다, iff 모든 distinct vertices에 대해 쌍방향(u에서 v, v에서 u)으로 path가 있다면.
strongly connected component란, strongly connected인 maximal subgraph이다.

> degree <
특정 vertex의 degree는 그 vertex에 연결된 edges 수이다.
digraph에서는 in-degree(해당 vertex가 head인 edge의 개수)와 out-degree(해당 vertex가 tail인 edge의 개수)를 추가로 정의한다.

ADT(Graph)

p.271
functions으로 Create, InsertVertex, InsertEdge, DeleteVertex, DeleteEdge, IsEmpty, Adjacent 를 정의한다.

6.1.3 Graph Representation

가장 흔히 사용되는 세가지 표현법만 알아보자.
어떤 representaion을 사용할지는 적용할 곳이나 수행할 기능에 달렸다.

6.1.3.1 Adjacency Matrix

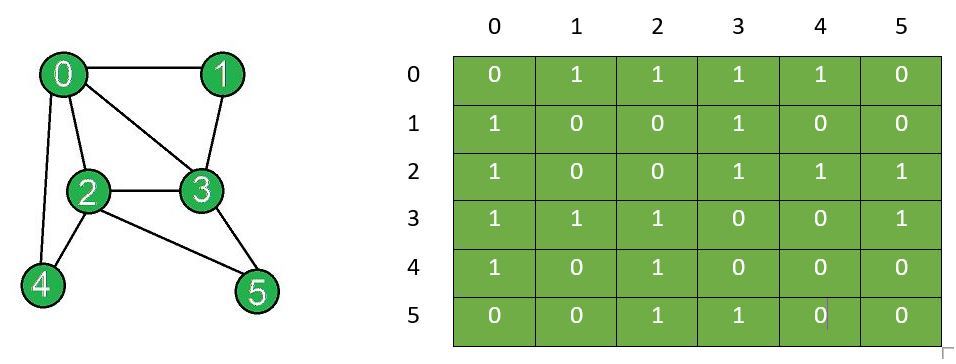
n×n의 2차원 배열로 나타낸다. 각 행렬이 vertex를 나타내고, edge가 존재하면 이를 표시한다.
(i,j) edge가 있다면, a[i][j]와 a[j][i]에 1을 저장한다. 나머지 값은 0이다.
digraph라면, <i,j>일때 a[i][j]에만 1을 저장한다.

undirected graph라면 matrix가 symmetric(대칭)이다. 따라서 위쪽이나 아래쪽 삼각형만을 저장해 공간을 절약할 수 있다.

undirected graph에서 특정 vertex의 degree는 해당 row의 합이다.
directed graph에서는 특정 row의 합이 해당 vertex의 out-degree이다.

단점
"몇개의 edges가 있나?", "해당 graph는 connected 인가?"
같은 질문의 답을 찾으려면 최소 O(n^2)이다.
표현법을 바꿔서 실제 존재하는 edges들만 저장하면 더 빨라질 것이다.

6.1.3.2 Adjacency Lists

chain의 배열로 나타낸다.
각 chain은 특정 vertex에 연결된 vertex를 저장한다.
(배열을 통해 any vertex에 O(1) time으로 접근할 수 있다.)

undirected라면 (i,j)일때 각각 두개의 chain을 저장하지만,
directed라면 <i,j>일때 adList[i]에만 j를 연결한다.

그래서 전자의 경우 vertex의 degree를 알고 싶으면 해당 chain에서 숫자를 세면 되지만,
후자의 경우 그렇게하면 out-degree만 알 수 있다.

directed graph에서 in-degree도 구하고 싶으면 혹은 모든 adjecent vertex로 접근하고자 한다면, inverse adjacency list를 만들어 두면 된다.
(그런 경우가 많다면 만들어둘 가치가 있다)
(보니까 그냥 directed일때 반대 방향을 저장해두는거 같음, 그냥 adjacent vertex 찾기위해)

다른 표현법

Chapter 4에서 했듯이, sparse matrix(adjacency matrix가 sparse인 경우 sparse matrix도 좋지)를 그냥 chain으로 그대로 표현한다.(말고 그 전에 했던 것처럼 구조체 배열로 존재하는 값만 저장하는 방법도 가능할 것 같네)
node 앞쪽 2개 fields는 head, tail을 나타내고, 뒤 2개 fields는 row와 column chain을 나타내게 한다.

chain의 배열이나 chain 말고, 그냥 쌩 1차원 배열로도 나타낼 수 있다.
총 n+2e+1만큼의 공간이 필요한데(n: vertex개수, e: edge개수),
0~i까지는 vertex i의 adjacency vertex를 저장할 공간의 starting point를 저장한다.
즉 vertex i에 대한 정보는 사실 node[node[i]]~node[node[i+1]-1] 에 저장된다.

6.1.3.3 Adjacency Multilists

adjacency list에선 vertex를 중심으로 나타내서 하나의 edge마다 두개의 공간이 필요했다.
이번엔 edge를 중심으로 표현하고, 해당 edge가 examine됐는지 mark할 수 있는 방법을 알아보자.

multilist(하나의 node를 여러 list에서 공유하는 형태)를 사용하면 쉽게 할 수 있다.
edge 하나당 node 하나를 만들고, 각 node(edge)는 2개의 list에 공유된다.
당연히 공유되는 list는 해당 edge에 연결된 두 vertex list이다.

m	vetex1	vertex2	link1	link2

node(edge)는 위 구조를 갖는다.
(i,j) edge라면 vertex1에 i, vertex2에 j가 저장되고(반대로해도 상관 X),
m field엔 해당 node를 방문했는지 등의 정보를 표시할 수 있도록 한다.
link1과 link2에는 해당 vertex와 연관된 다음 edge node를 연결해준다.

하나의 edge를 2개의 vertex list가 공유하므로, 각 list의 다음 node를 link로 걸어주려면 당연히 2개의 link가 필요하다.
link1은 vertex1 list의 다음 link이고, link2는 vertex2 list의 다음 link이다.

(위 그림은 보기쉽게 중복해서 그린 것, 사실 node는 6개뿐이다. 두군데 공유되기때문에 12개로 보인다.)

vertex 순서에 따라 맞는 link를 타고가면 해당 list의 다음 node가 나온다.
(책에는 아래와 같이 표현돼있다.)

사용하는 공간은 일반적인 adjacency list와 같다.
node수는 2배로 적지만 한 node가 2배의 공간을 차지하기 때문이다.

6.1.3.4 Weighted Edges

Graph에 weight 정보를 포함해 다른 vertex로 가는데 거리나 비용 등을 표시할 수 있다.
이를 network라고 한다.

adjacency matrix에서 표현하려면 그냥 1 대신 weight를 저장하면 되고,
adjacency list에서 표현하려면 node에 field를 하나 추가해서 저장하면 된다.

representation 방법을 보면,
tree에선 직접적으로 tree를 link로 만들든지 array로 만들든지 했는데,
graph는 그냥 vertex간의 관계 정도를 표현하네.
잘 고려해서 연산 수행하자.

6.2 ELEMENTARY GRAPH OPERATIONS

tree에선 traversal이 가장 흔히 사용되는 operation이었다.
graph에서도 이와 비슷한 Depth First Search와 Breadth First Search를 알아보자.

(모두 adjacency list로 표현됐다고 가정/다른 표현법도 가능)

6.2.1 Depth First Search(DFS)

> 과정(말로 풀어서) <
starting vertex v를 visit하며 시작한다.
v의 adjacency list에서 방문하지 않은 vertex w를 고른다.
그리고 w에 대해 다시 DFS를 수행한다.
추가로, w에 대해 DFS를 수행하기 전에,v의 adjacency list를 어디까지 진행했는지에 대한 정보를 stack에 넣어준다. 위 예시라면 w까지 진행했으니 그 정보를 저장해둬야 한다.
그래야 다시 돌아왔을때 시작할 위치를 알 수 있다.

그렇게 계속 하다가 들어가다가 보면 adjacency list 중에 unvisit한 vertex가 없는 순간이 온다.
그때 stack에서 pop하고, 방문하지 않은 adjacency list를 찾아서 그곳으로 간다.
stack empty이면 search는 종료된다.
(preorder traversal과 비슷하다.)
(preorder와 차이점은 tree는 방문한 node인지 검사할 필요가 없지만, graph는 cycle이 있을 수 있어서 방문했는지 확인해야 한다.)

> 구현 <
stack을 사용하는 대신, recursive function으로 구현
(system stack을 쓰긴하네)
code보면 알겠지만 길이 막혀서 다시 돌아오면 adjacency list 처음부터 보는게 아니라 하던 부분부터 시작한다.

void dfs(int v) {
	nodePointer w;
    visited[v] = TRUE;
    printf("%5d ", v);
    for (w = adjList[v]; w; w = w->link)
    	if (!visited[w->vertex])
        	dfs(w->vertex);
}

// DFS는 그냥 간단하게 재귀 호출되며 방문할 때마다
// visited 했다고 체크해주면 된다.
// BFS는 이렇게 하면 큐에 쓸모없는 값이 들어갈 수 있어서
// 큐에 넣기 전부터 visited 했다고 체크해준다.

이를 통해 우리는 특정 vertex v에 연결된 모든 vertex를 visit할 수 있다.
즉, dfs를 통해 visit한 vertices와 edges는 해당 graph의 connected component를 형성한다.

adjList의 각 원소 값 자체가 adjecency vertex를 바로 가리킨다는 것에 주의해야한다.
즉, 특정 vertex n의 adjecency vertex로 가기위해선 adjList[n]->link 가 아니라, adjList[n]이다.

하나 더 언급할만한건, if로 visited인지 확인하고 함수를 호출한다.
binary tree traversal 함수도 이런식으로 검사하고 재귀호출하면 호출횟수 줄일 수 있지않을까 싶다.
무작정 호출부터 해버리면 system stack 소모..(그렇게 크진 않나?)

Analysis (dfs)
adjacency list의 node를 최대 1번씩 검사하므로, O(e)이다.
(adjacency list에서의 node 개수를 edges 개수와 비례한다.)

adjacency matrix였다면, O(n^2)이었을 것이다.

dfs using stack

여기 그림 참고

binary tree traversal 할때, recursive 버전에서 system stack이 하듯이, stack 만들어서 iterative 버전으로 변경할 수 있었다.
dfs using stack 같은 경우도, 재귀에서 system stack이 넣듯이 넣는다.
위 링크 봐선 그렇게 안 보일수도 있는데,,,
일단 dfs를 하려면 어디까지 진행했었는지의 정보가 필요하다, 예를들어 3번 node에서 해당 node의 인접 노드 중 어디까지 돌아보다가 stack에 저장됐는지에 대한 정보 같은 것이다. stack에서 빼고 처음부터 모든 인접 노드를 visited로 확인해도 작동은 잘 하겠지만, 효율적으로 구현하자면 그렇다.
뭐 어쨌든 그걸 저장해서 stack에 넣어야 하는데, 위 링크에선 그러지 않고 그냥 다음 진행해야할 vertex를 다 stack에 넣어준 것 뿐이다. -> 이렇게 생각하면 큰 차이는 없음.
(tree는 어디까지 진행했는지에 대한 정보가 left,right 수준이라 system stack과 비슷하게 직관적으로 구현할 수 있었다.)

위 링크 code보면 if문을 두개나 써가면서 visited를 확인한다.
visited 확인하고 stack에 넣으면 되지않나 라고 생각할 수 있는데, 그렇게 하면 같은 vertex가 stack에 두번 들어갈 수도 있다.
recursive 버전과 다르게, 우리는 그냥 stack에 다 넣고있기때문에 stack에서 뺄때 visited인지 확인할 필요가 있다.

6.2.2 Breadth First Search(BFS)

> 과정(말로 풀어서) <
v를 방문하며 시작하고, 이를 visited로 표시한다.
그리고 v의 adjacency list의 vertices를 하나씩 모두 방문한다.
그렇게 다 돌고나면 v의 adjacency list 중 첫번째 vertex의 adjacecy list의 vertices를 방문한다.
이를 위해 queue를 활용한다.
즉, 한 vertex의 adjacency vertices를 방문하며 queue에 집어넣는다.
다 방문하고나면 queue에서 하나 빼서 걔의 adjacency vertices를 모두 방문한다.
queue empty이면 search는 종료된다.
(level order traversal과 비슷하다.)

> 구현 <
queue는 int type을 저장하는, dynamically linked queue이다.

void bfs(int v) {
	nodePointer w;
    front = NULL, rear = NULL;  //초기화
    
    visited[v] = TRUE;
    printf("%5d ", v);
    addq(v);
    
    while (front) {  //front가 NULL이면 끝
    	v = deleteq();
    	for (w = adjList[v]; w; w = w->link) {
        	if (!visited[w->vertex]) {
        		visited[w->vertex] = TRUE;
   				printf("%5d ", w->vertex);
            	addq(w->vertex);
            }
        }
    }
}

dfs와 마찬가지로, bfs를 통해 visit한 vertices와 edges는 해당 graph의 connected component를 형성한다.

Analysis (bfs)
adjacency list로 구현됐다면, vertices의 degree를 모두 더한만큼 examine한다.
따라서 O(e)이다.

adjacency matrix였다면 O(n^2)이다.

DFS와 BFS 코드 차이

둘이 visted를 체크하는 위치같은게 좀 차이가 있는 것 같아서 일반화해서 생각해보려고 정리도 해보고 했는데, 굳이 그럴 필욘 없는 듯, 시간낭비인 것 같다.
그냥 DFS는 DFS 코드 대로 BFS는 BFS 코드 대로 따로따로 이해해서 적용하는게 맞는 것 같다.
DFS 코드 보면, 일단 한 노드 방문처리하고, 걔 주변에 방문하지 않은 인접 노드로 가는 거고!
BFS 코드 보면, 일단 첫 노드를 방문 처리 하고 queue에 넣고, 걔를 dequeue하고 인접 노드 중 방문하지 않은 노드들을 방문처리하면서 queue에 넣고를 반복하는 것이고!
그냥 따로따로 잘 이해되니까 그렇게 이해하고 외우고 말자. 뭐 왜 굳이 이렇게 짰을까 일반화 시키면서 고민하는건 좀 시간낭비인듯... 그런 고민을 하고 짠 코드란 보장도 없고... 실제로 해보려고 몇십분 고민해봤는데 너무 사소한거에 집착하는 것 같아서 그냥 이렇게 "따로 이해하고 외우는게 맞다"고 느낌.
(BFS는 DFS stack 버전 처럼 아마 queue에서 빼면서 방문 처리를 해도 되지 싶은데, 그러면 BFS 반복문내 코드 상단에 방문 여부를 확인해야되고, 중복 노드가 들어가서 오히려 비효율적이라 queue에 넣는 행위 자체를 방문으로 처리한듯. 그거 생각하고 이해하면 쉬움.)
(그렇다고 DFS stack 버전도 BFS처럼 stack에 넣을 때마다 방문 처리를 하는 건 안됨! BFS는 queue에 넣는 순서대로 방문하지만, DFS는 stack에 넣었던 노드가 더 위에 추가된다면 위에 추가된 놈 기준 순서로 방문되기 때문!)

6.2.3 Connected Components

말했듯이, dfs나 bfs를 이용해 connected components를 찾을 수 있다.

> connected component를 line별로 출력 <

void connected(void) {
    for (int i = 0; i < n; i++)  //n은 vertex 개수
    	if(!visited[i]) {
        	dfs(i); 			 //bfs(i)여도 OK
            printf("\n");
        }
}

analysis (connected)
adjacency list라면, dfs하는데 O(e), for문도는데 O(n),
따라서 총 O(n+e)

adjacency matrix라면, O(n^2)

6.2.4 Spanning Trees

graph G의 모든 vertices를 포함하고, E(G)의 부분집합인 edges를 가지고 있을때 이를 Spanning tree라고 한다.
추가로, Spanning tree는 특정 graph의 conncted minimal subgraph이다.
minimal subgraph란, 최소 edges 수를 가져야 한다. connected여야하니, n개의 vertices가 있다면 n-1 개의 edges가 있다.
spanning tree는 최소 edges를 가져야해서 cycle이 없다.

graph가 connected 돼있다면, dfs나 bfs를 했을때 edges는 tree edge인 T와 nontree edge인 N으로 나뉜다.
search할때 if문 내에서 edges들만 따로 저장해주면 tree edge를 구할 수 있다.
dfs나 bfs를 통해 spanning tree를 구할 수 있는데, 이를 각각 depth first spanning tree, breadth first spanning tree라고 한다.

Tree와의 차이?
graph의 부분집합인 tree들을 spanning tree라고 한다.(spanning + tree)
tree는 원래부터 tree.
Difference between a tree and spanning tree

6.2.5 Biconnected Components

G는 undirected connected graph라고 먼저 두겠다.
G에서 특정 vertex v와 거기에 연결된 edges를 모두 제거했을때 두개 이상의 connected component로 분리된다면, v를 articulation point라고 한다.

biconnected graph란 articulation point가 없는 graph를 말한다.
(대부분 실제 graph 사용에서 articulation point는 지양된다. 위 graph를 communication network라고 했을때 point가 끊겨버리면 나머지 기능이 제대로 작동하지 않을 수 있기 때문이다.)

biconnected component란 maximal biconnected subgraph이다. 즉, 해당 biconnected component를 포함하는 더 큰 biconnected subgraph는 없단 소리다.

> biconnected component 구하기 <
biconnected component를 구하려면 dfs를 이용하면 된다.(정확히는 dfn)
dfs를 적용하면 spanning tree를 구할 수 있다.
dfs를 사용했을때 나오는 vertices의 순서가 있는데 이를 depth first number(dfn)이라고 한다.
vertex u가 vertex v의 depth first spanning tree의 ancestor라면 dfn(u) < dfn(v)이다.

> articulation point 찾기<
dfs를 통해 spanning tree로 바꾸게 되면, 원래 있던 edges들이 T와 N으로 분리된다고 했다.
여기서 N(non tree edges)으로 연결되는 두 vertices가 ancestor 관계라면, 해당 edges를 back edge라고도 한다.(그 edge를 통해 세대를 올라갈 수 있어서 그런가)
dfs를 통해 나온 N(non tree edge)은 모두 back edge인데, non tree edges가 애초에 dfs 후 spanning tree의 조상-후손 간에만 생길 수 있기 때문이다.

조상-후손간 말고 반대편 line으로 non tree edge가 날 순 없다.
dfs하면 전부 같은 line으로 정리된다, 좀만 생각해보면 알 수 있음.

따라서,
(1) depth first spanning tree의 root의 children이 2개 이상이라면 이 root vertex는 articulation point이다.
(2) depth first spanning tree의 특정 vertex v가 최소 1개의 child를 가지고 있고, 그 child의 decendants나 그 아래의 single back edge를 통해서 v의 ancestor로 갈 수 없다면 v는 articulation point이다.

(2) 조건은 말그대로, v의 ancestor로 갈 수 있단 소리는, v를 끊어내도(articulation point로 잡아도)
다른 부분과 연결이 돼있어서 articulation point가 될 수 없단 뜻이다.

(2) 조건은 dfn을 이용해 다시 해석할 수 있다.
(2) vertex v는 child w를 가지는데, 이에대해 low(w) >= dfn(u)라면 v는 articulation point이다.

low(w) 함수는 특정 vertex의 decendants가 그 ancestor과 연결됐는지 확인할 수 있게 해준다.
low(w)의 값은 w 본인과 child들, 혹은 한번의 back edge를 통해 갈 수 있는 최소 dfn이다.(w보다 이 값이 더 작으면 ancestor로 갈 수 있단 뜻)
(x값에 보통 확인하려는 vertex의 child를 넣는다.)

> dfn & low functions <
dfn과 low 값을 구하는 함수, dfs 함수를 수정하여 만든다.
dfn과 low 배열은 전역
visited 배열을 따로 만들지 않고, dfn을 -1로 초기화해서 visited를 구분한다.
int num = 0;을 전역으로 선언해 저장할 dfn 값을 1씩 늘려준다.

void dfnlow(int u, int v) { //v is parent of u(if any)
	//u가 starting point
    
	nodePointer ptr;  //'u' vertex의 자식들을 훑기위한 pointer

    dfn[u] = low[u] = num++;
    
    for (ptr = adjList[u]; ptr; ptr = ptr->link) {  //ptr은 vertex u의 child를 가리킴
    	if (dfn[ptr->vertex] < 0) {  //not visited
        	dfnlow(ptr->vertex, u);
            low[u] = MIN(low[u], low[ptr->vertex]);  //재귀호출 끝나고 다시 올라올때 low값 update
        }
        else if (ptr->vertex != v)  //방문은 한 node지만, 부모가 아닌 경우
        //방문한 node는 back edge를 통한 vertex란 소리이므로 low값 update
        //adjList에선 부모 node도 포함되기때문에 구분해야한다.
        	low[u] = MIN(low[u], low[ptr->vertex]);
    }
}

dfn은 그냥 쭉 순서대로 assign해주면 돼서 쉽다.
문제는 low인데, 일단 dfn과 같이 쭉 assing해주고,
다시 돌아오는 과정에서 값을 재측정해야한다.
그래서 재귀호출 뒤에 그 과정이 있는 것이다.

dfnlow(x,-1) 형식으로 호출한다.

> bicon function <

connected graph의 edges를 biconnected components들로 분리해보자.

(dfnlow를 좀 수정해서 만듦)
edges들을 stack에 저장하다가(모두 저장),
low[w] >= dfn[u]인 지점(articulation point)을 만나면 그 부분까지만 stack에서 빼서 출력하는 형식으로 biconnected components를 구할 수 있다.

initialize
마찬가지로 dfn과 low를 -1로 초기화하고,
dfn으로 visited를 구분한다.

void bicon(int u, int v) {
	nodePointer ptr;  //'u' vertex의 자식들을 훑기위한 pointer
    int x, y;

    dfn[u] = low[u] = num++;
    
    for (ptr = adjList[u]; ptr; ptr = ptr->link) {
        /* 바로 아래 if문, stack에 edge push(추가된 부분1)
         * dfs 경로 상의 모든 edges를 push해둔다.
         * dfs를 진행하며 adjList를 훑는데, 그 중 부모로 다시 가는 edge는 중복이므로 제외(조건1)
         * 제외(조건2)
         */
    	if (ptr->vertex != v && dfn[ptr->vertex] < dfn[u])
        	push(u, ptr->vertex);
    
    	if (dfn[ptr->vertex] < 0) {  //unvisited vertex
        	bicon(ptr->vertex, u);
            low[u] = MIN(low[u], low[ptr->vertex]);
            
            if (low[ptr->vertex] >= dfn[u]) {
            //articulation point 발견, stack에 저장된 edges 출력(추가된 부분2)
            	printf("new biconnected component: ");
                do {  //biconnected component 출력
                	pop(&x, &y);
                    printf(" <%d, %d>", x, y);
            	} while(!((x == u) && (y == ptr->vertex)));
            	printf("\n");
        	}
        }
        else if (ptr->vertex != v)
        	low[u] = MIN(low[u], low[ptr->vertex]);
    }
}

bicon(x, -1) 형식으로 호출한다.

위 코드 그대로 잘 짜봤는데 cycle있으면 bicon이 어느정도는 나오는데, 완전 제대로 출력이 안됨.
흐름 정도 참고만 하자.

QnA
dfn[u]와 low[ptr->vertex]가 같은 경우가 있나? 큰 경우에서만 articulation 아닌가?
: u vertex의 자식(dfs로 했을때 자식)이 descendants의 back edge로 u로 올 수 있다면, 두 값은 같고, u는 articulation point이다.

analysis (bicon)
O(n+e)

6.3 MINIMUM COST SPANNING TREE

minimun cost spanning tree는 특정 graph에서 만들어질 수 있는 최소 cost의 spanning tree이다.

Greedy method로 분류되는, 최소신장트리를 구하는 세가지 algorithms을 알아보자.
(Kruskal's, Prim's, Sollin's)

greedy method란, stage별 가장 최적의 해답을 이용해 문제를 풀어나가는 것이다.
(눈 앞에 보이는것만 최적으로 해서 greedy인듯..)
특정 제한사항에서 실현 가능한 최적의 solution으로 단계별로 해결한다.

Munimum cost spanning tree contraints
1) graph의 edges만을 사용해야한다.
2) 정확히 n-1개의 edges만을 사용해야한다.
3) cycle을 만드는 edge는 사용할 수 없다.

6.3.1 Kruskal's Algorithm

edge 하나씩 더해가며 Minimum cost spanning tree T를 만든다.
(T는 edge의 집합)

방법
1) 선택되지 않은 edges 중 최소 cost를 갖는 edge를 더한다.
2) 만약 이 edge가 cycle을 형성하면 무시하고 다음 최소 cost edge를 본다.
3) 1~2를 n-1 edges를 더할 때까지 반복한다.

Implement

1) G의 edges 집합 E에서 최소 cost edge를 찾을 수 있어야하고,
2) 해당 edge가 cycle을 형성하는지 판단할 수 있어야 한다.
+) graph 구현은 어차피 edge가 중요하니, edge 구조체 만들어서 집합으로 표현해도 ㄱㅊ을듯. 굳이 위에서 배운 구현법 중에 쓰는게 아니라.

1번은 sorting을 이용해 O(e loge) time으로 정렬할 수도 있고,
min heap을 이용해 최솟값 찾고 뽑아내는데 O(loge) time으로 할 수도 있다(min heap 구축은 O(e)).

2번에서 cycle을 판단하려면, union-find operation을 이용한다.
초기엔 모든 vertices를 각각의 set으로 간주하고, spanning tree로 연결될때마다 set이 union된다.
연결하려는 각 vertices는 find operation으로 어떤 set인지 찾고,
만약 이미 같은 set이라면 그 둘을 연결하려는 edge는 cycle을 형성하는 것이기 때문에 무시한다.

ex) {1,2,3}, {5} 까지 일단 만들어져있는데, (2,3) edge가 추가되려고한다.
이때 2와 3은 같은 set에 있으므로 (2,3) edge는 거부된다.

pseudo code

T = {};
while (T contains less than n-1 edges && E is not Empty) {
	choose a least cost edge (v,w) from E;
    delete (v,w) fron E;
    if ((v,w) does not create a cycle in T)
    	add (v,w) to T;
    else
    	discard (v,w);
}

if (T contains fewer than n-1 edges)
	printf("No spanning tree\n");

Time Complexity
union-find는 choosing-deleting보다 적은 시간이 걸린다.
따라서 $O(E \log E)$
(E는 edges 개수)

kruskal $EO(\log E)$ 맞는 것 같은데 $E(\log V)$ 라고 하는 곳이 많다. 왜지?
: $E \leq V^2$ 이므로 $\log E \leq 2\log V$ 이다. 따라서 후자와 같이 적어도 상관없다.
(위에 properties 보고오면, undirected graph에서 edge 최대 수는 v(v-1)/2임. 따라서 e <= v^2 성립)
답변

Theorem 6.1

G가 undirected connected graph일때 Kruskal's algorithm이 minimum cost spanning tree를 찾는지 증명

(a) Kruskal's method가 spanning tree를 만드는지(spanning tree가 있다면)
(b) 그렇게 만들어진 spanning tree가 minimum cost인지
보인다.

자세한 증명 과정은 p.293 아래부터..

여기 쉽게 잘 설명돼있음

6.3.2 Prim's Algorithm

edge 하나씩 더해가며 Minimum cost spanning tree T를 만든다.
(T는 edge의 집합)
Kruskal과의 차이는 더해지는 edge가 tree를 이루어야 한단 것이다.(크루스칼은 그냥 forest였음)

방법
(1) T에 일단 아무 vertex를 잡는다.
(2) T와 합쳤을때 tree를 이루는 최소 cost edge (u,v)를 찾는다.
(3) (u,v)가 cycle을 형성하면 무시하고, 아니라면 T에 추가한다.
(4) 2~3번 과정으로 T가 n-1개 edges를 가질때까지 반복한다.

pseudo code

T = {};
TV = {0}; //TV에 선택된 vertex들 저장, 0부터 시작

while (T contains fewer than n-1 edges) {
	let (u,v) be a least cost edge such that u∈TV and v!∈TV;
    if (there is no such edge)
    	break;
    add v to TV;
    add (u,v) to T;
}

if (T contains fewer than n-1 edges)
	printf("No spanning tree\n");

time complexity: $O(v^2)$ (adjacency matrix로 표현할 경우)
adjMatrix로 표현하면, vertex가 set에 추가될때마다 dist를 update해야한다.
한번 update하는데 $v$ , 이를 총 $v$ 번 해야하니 $v^2$ 이다.
(dist 배열 사용 안하더라도 결국 모든 element를 봐야하니 $v^2$ 이다. 이것보다 늦게 걸리는 작업은 없다. 정렬도 O(e log e)이고..)
kruskal은 adjecency matrix로 잘 안하고 그냥 edge 정보만 입력받아서함. 그래서 kruskal이 $v^2$ 이 아닌 것이고, prim도 matrix로 해서 $v^2$ 이지 이 경우처럼 adjList로 표현하거나 Fibonacci heap(Chapter 9)을 사용하면 더 적게 걸린다.

Kruskal VS Prim
edge가 많으면 prim이 유리
(vertex에 비해 edge가 많다면 prim, 그게 아니라 sparse graph라면 kruskal)

나는 구현할때, kruskal 바탕으로 minimum edge로 선택될 수 있는 후보 edges를 따로 관리하는걸 추가함.
그래서 그 후보 중에 최소 찾고.. 하는 식으로,.. 후보면 배열에 해당 edge number가 TRUE로 마킹되도록
뭐 후보 배열 따로 안 만들고 edge 정보에 포함시켜도 ㄱㅊ긴할듯

교수님 강의자료나 다른 곳에선 거리 배열 dist를 유지하며 구한다.
곧 바로 연결 안돼있으면 INF로 처리하며, vertex가 set에 추가될때마다 dist를 재조정

kruskal이든 prim이든 selected[] 배열 유지하며 방문한 곳 체크는 당연히 해야됨

6.3.3 Sollin's Algorithm (Boruvka)

sollin은 하나의 edge가 아니라 여러 edges를 T에 추가한다.
모든 vertices를 분리된 별도의 tree로 보고, 각 tree끼리 최소로 연결하며 하나의 tree가 될때까지 반복한다.

방법
1) 처음엔 모든 vertices 각각을 하나의 spanning tree로 본다.
2) 각 tree에서 다른 tree와 연결된 가장 적은 cost의 edge를 선택한다. edge를 중복 선택할 수 있으니 주의한다.
3) 2번 과정을 반복한다. tree가 1개만 남거나, 선택할 edge가 없을때 종료된다.

cycle test는 할 필요가 없다. 어차피 각 단계가 spanning tree끼리 edge하나로 연결되는 거기 때문에 cycle이 존재할 수 없다.
spanning tree와 spanning tree를 edge 하나로 연결하면 cycle은 존재하지 않는다. 처음 시작에 전부 spanning tree이므로 cycle은 없다.

또 kruskal이나 prim처럼 edge를 sort할 필요도 없다.

또 kruskal이나 prim에 비해 쉽게 병렬로 수행될 수 있다.(한 선택이 다른 곳에 영향을 딱히 안미친다.)

보루프카 알고리즘

6.4 SHORTEST PATHS AND TRANSITIVE CLOSURE

googleMap 같은데서 두 지점 사이 경로를 찾아줄때 보통 graph를 사용한다.

여기선 length, cost, weight 다 같은 말로 쓰인다.
path의 starting vertex는 source, 마지막은 destination이라고 한다.
digraph(directed-graph)는 일방통행로를 표현할때 사용한다.

6.4.1 Single Source/All destinations: Nonnegative Edge Costs (Dijkstra)

directed graph G = (V,E)가 있다고 해보자. source는 v0이다.
source로부터 각 vertex까지의 shortest path를 찾아보자.

> greedy algorithm 이용 <
source v0로부터 shortest path를 찾은 vertex를 nondecreasing order로 S에 넣는다.
greedy니까 일단은 source로부터 바로 갈 수 있는 가장 짧은 vertex부터 S에 넣는다. 그럼 걔는 shortest path가 고정된거다.
(예를들어 v0 ~> v1로 바로 가는 길이 v0의 인접vertex로 가는 길 중에 가장 작으면, 돌아서오는 길(ex. v0 ~> v2 ~> v1)은 당연히 더 클테니 얘로 가는 길은 그게 최소인게 당연)
이렇게 S의 인접 vertex(== S에 포함되지 않는 vertex)들부터 차근차근 살펴나가며 최소 cost path를 찾는 것이다.

v0부터 (S에 있지 않은) w까지 S의 vertices를 통해서 가는 shortest path를 distance[w]라고 하자.

(1) v0로부터 S에 포함되지 않는 vertex u로의 shortest path를 찾으려면, S의 vertices를 무조건 지나야 한다.
증명 : 만약 S에 포함되지 않는 vertex w가 u로의 shortest path에 있다고 해보자. 그럼 모순인게, S가 가장 짧은 path를 nondecreasing order로 저장하기 때문에 w는 S에 포함돼야한다.

(2) S에 있지않은 vertices 중에 최소 distance(distance[u])를 가지는 u를 S에 추가한다.(값이 같으면 그중 암거나)

(3) 이렇게 u가 S에 추가되면 S 밖의 vertex(w)의 distance가 바뀔 수 있다. u를 통한 path가 더 짧을 수 있기 때문이다.
이 더 짧은 path의 중간 vertices는 모두 S에 있고, u에서 w로 가는 path는 바로 연결된다. distance[u]+length(<u,w>)
(path의 intermediate vertices는 (1)에 의해 S에 있을 수 밖에 없다. S에 추가된 vertex는 u뿐이므로 u를 통한 경로가 최소 경로 후보에 오를 수 있는 것이다.)
(그럼 u에서 w까지 바로가는게 아니라, u 다음 S내의 다른 경로를 통할수도 있지않나? : ㄴㄴ, S내의 다른 경로라 함은 u보다 먼저 들어왔으므로 v0에서 u까지의 경로보다 cost가 더 작은 경로라는 소리다. 그런데 u를 통해 S내에 미리 있던 다른 vertex로 간단 것은 더 긴 경로로 돌아가겠다는 것이라서 말이 안된다. 최소 경로후보가 될 수 없다.)

위 방법은 Edsger Dijkstra가 고안한 방법이다.

Implement (Dijkstra Algorithm)

각 vertices는 0~n-1을 나타내도록 하고,
found array를 사용해 S에 포함되는지 확인한다.
graph는 cost adjacency matrix를 이용해 표현한다.
없는 edge의 경우 matrix에 엄청 큰 숫자를 저장해서 표현한다.(overflow 발생하지 않게 적당히 커야한다.)
<i,i> edge의 경우 결과에 영향 안주는 nonnegative number로 한다.
(기존에 없는 edge는 0으로 표시했었는데, 0이나 -1로 저장해서 따로 다루느니 그냥 큰 숫자를 넣으면 한번에 다룰 수 있다.)

/*
 * v는 시작 vertex, cost는 graph나타낸 adjacency list,
 * distance는 S에 vertex가 추가될수록 update된다.
 * choose 함수를 통해 다음으로 가장 가까운 vertex를 찾는다.
 * 돌고나면 distance에 거리들 쭉 저장돼있을거임
 * shortest path는 아래 code좀 수정해서 저장하면 된다.
 */
 
void shortestPath(int v, int cost[][MAX_VERTICES],
int distance[], int n, short int found[])	{
	int i, u, w;
    for (i = 0; i < n; i++) {  //found, distance 초기화
    	found[i] = FALSE;
        distance[i] = cost[v][i];
    }
    
    found[v] = TRUE;  //시작 vertex S에 추가
    distance[v] = 0;
    
    for (i = 0; i < n-2; i++) {
    	//n-2인 이유는 처음 vertex 제외하고, 마지막 남은 애는 굳이 안뽑아도 distance 계산되기때문
        u = choose(distance, n, found);
        found[u] = TRUE;  //u를 S에 추가
        for (w = 0; w < n; w++)  //u에 연결된 w들 distance update(전부 update되긴함)
        	if (!found[w])
            	if (distance[u] + cost[u][w] < distance[w])
                	distance[w] = distance[u] + cost[u][w];
    }
}

int choose(int distance[], int n, short int found[]) {
	//간단하게 distance 제일 작은 애 반환해준다.
	int i, min, minpos;
    min = INT_MAX;
    minpos = -1;
    for (i = 0; i < n; i++)
    	if (distance[i] < min && !found[i]) {
        	min = distance[i];
            minpos = i;
        }
    return minpos;
}

/*
min vertex 구하려면 선택되지 않은 애들 중에 해야돼서 나는 min 초기값 잡으려고 반복문 하나 더 썼었는데
이 방식이 compact하고 좋네
*/

Analysis (shortesPath)
딱보면 알겠지만 O(n^2)이다.
adjacency matrix로 graph 표현해서그런데, 이런 algorithm은 이론상 O(e)까지도 가능하다. 하지만 matrix로 표현하면 최소 O(n^2)이다.(다 봐야되니)

Chapter 9에 나오지만,
이렇게 single-source all-destination problem을 greedy algorithm으로 접근한 경우
adjacency list와 fibonacci heap을 사용하면 더 효율적으로 구현할 수 있다.

6.4.2 Single Source/All Destinations: General Weights (Bellman-Ford)

directed graph에서 negative cost도 포함된 경우

negative cost도 고려하려면, negative length cycle이 없어야 한다. 그 cycle 돌면 cost가 계속 줄어들기 때문이다.
$dist^l[u]$ 는 최대 l개의 edges를 이용해 u까지 갈 수 있는 최소 거리라고 해보자.
( $dist^1[u] = length[v][u]$ )
우리는 모든 edge u에 대한 $dist^{n-1}[u]$ 를 찾아야 한다. negative cycle은 없다고 했고, 그냥 cycle이 있더라도 그걸 이용하면 당연히 최소 거리가 될 수 없으므로 n-1 edges 내로 찾아야한다.
n-1개 edges 초과해서 사용해서 가면 무조건 돌아가는게 되므로 거리가 멀어진다.

dynamic programming methodology를 이용해 풀자.
(1) v에서 u까지의 $dist^k[u]$ 가 실제로 k-1개 이하의 edges를 사용했다면, $dist^k[u] = dist^{k-1}[u]$ 이다.
(2) v에서 u까지의 $dist^k[u]$ 가 딱 k개의 edges를 사용했다면, <i,u>edge를 가진 i에 대해 $dist^k[u] = dist^{k-1}[i] + length[i][u]$ 이다. (우변은 최솟값이 나오도록 하는 i)

즉,
$dist^k[u]=min(dist^{k-1}[u], min(dist^{k-1}[i] + length[i][u]))$
(재귀형태로 정의된다.)

위 재귀 식을 이용해 k=1일때부터 n-1까지 dist 배열을 업데이트 시킨다.
반복문을 통해 반복하며 $dist^1$ 부터 $dist^{n-1}$ 까지 dist를 업데이트 한단계씩 시킨다.

(쉽게말해서 dijkstra는 방문하지 않은 node들만 업데이트하며 거리를 확인했지만, bellman-ford는 node를 방문(?)하며 다른 모든 node의 거리도 업데이트한다. dijkstra는 negative가 없어서 바로 결정 났지만 이 경우엔 다른 경로가 더 짧을수도 있어서..)
여기선 node를 방문한다기보다는(dijkstra에선 방문하면 cost가 정해지니까), 반복문을 반복하며 사용하는 edge 수를 늘려가는 것이다.(방문개념이 아니라 selected[](found[]), choose[]도 필요없다.)
사용하는 edge수를 늘려가며, 더 적은 edge를 사용했을때 더 빠른지, 아니면 추가로 하나의 edge를 더 사용했을때 더 빠른 길이 있는지 다 찾아보며 update하는 것이다.
(edge가 1인 경우부터 n-1인 경우까지 최단거리를 각각 비교해 그 중에서의 최단 거리를 찾는 방식)

당연한 논리이다.
어떤 정점으로부터 다른 정점들까지 가는 최단거리는 1<=n<=e인 n개의 edge를 사용할 것이므로
1~e 개의 edge를 그냥 차근차근 모두 보는 것이다. 중복 부분 문제를 일반화하여 깔끔하게 푸는 것이다.
"어 다익스트라는 뭐지? 그냥 다 이걸로 풀릴거같은데?" 싶을 수도 있긴한데,
다익스트라는 음수 간선이 없으므로 좀 더 그 상황에 맞게 최적화된 알고리즘이다.
물론 이 알고리즘도 다익스트라가 적용될 경우에도 적용할 수 있지만 시간복잡도만 증가할 뿐이다.

void BellmanFord(int n, int v) {
	for (int i = 0; i < n; i++)
    	dist[i] = length[v][i];  //dist 초기화, dist^1을 계산한 것
    
    for (int k = 2; k <= n-1; k++)  //dist^2부터 시작(n-1까지)
    	for (v가 아니고, 1개 이상의 incoming edge가 있는 u)
        	for (each <i, u> in the graph)
            	if (dist[u] > dist[i] + length[i][u])
                	dist[u] = dist[i] + length[i][u];
}

Analysis (BellmanFord)
adjacency matrix라면 O(n^3), adjacency list라면 O(ne)

좀 더 빠르게 1
아래쪽 for문을 돌다가, 만약 dist를 한번 update했는데 바뀐 값이 없다면 다음 update에서도 당연히 바뀌는 값이 없다.(dist[u]나 dist[i]나 모두 그대로이기때문이다.)
그러니, 1~n-1까지 dist update를 진행하거나, dist의 값이 더이상 바뀌지 않는 부분에서 멈추면된다. 이러면 더 빨리 진행할 수 있다.

좀 더 빠르게 2
다른 방법은, dist 값이 바뀐 vertices를 저장하는 queue를 만드는 것이다.
이전 반복문에서 dist값이 바꼈다면, 다음 반복문에서 i의 후보가 될 수 있는건 얘네들 뿐이다.
queue내의 vertices들의 adjecency vertices만 보면서 진행하면 된다.(위 코드들 좀 수정해야됨)
값이 바뀐 애들은 다시 queue에 넣으며 queue가 빌때까지 계속한다.

고찰
직접 짜보니 저렇게 dits[]하나만으로 계속 업데이트를하게되면 반복문을 돌때 건너뛰는 경우가 발생한다.(좀 더 빠르게 부분 얘기하는게아니라 위에 코드 얘기)
예를들어 edge 3개일때의 dist를 update하려고한다고 해보자.
앞쪽 vertex들이 먼저 update되고 뒷쪽 vertex가 update되는데, 앞쪽에서 검사하다가 3개의 edge를 사용한 경우가 2개 이하 사용할때보다 더 작아서(if문 비교) dist가 update되면, 뒷쪽 vertex들은 해당 update된 vertex를 통해서 오늘 길을 볼때 사실상 edge 4개를 검사하는 셈이다.
그래서 위 pseudo code대로 작성 후 프린트하면 $dist^k[]$ 가 순서대로(생각한대로) 출력되지 않을 수 있다.
그래서 이 과정을 보고자 한다면 dist1[]과 dist2[]로 나눠서 update되는걸 따로 모아준 후, edge n개일때 쭉 update끝나면 갱신하고 하는 식으로 해야한다.

결과만 필요하다면 상관없다. 최소 distance가 나오는 edge를 뛰어넘을 수도 있지않나 생각하는데, 그럴 수는 없다.
즉, n개의 edge사용할때 최소 distance가 나온다면 n+1개로 바로 뛰어넘을 순 없단 소리다.
n개의 edge를 사용했을때 특정 vertex A까지 가는 최단경로가 있다고 가정해보자. 그럼 그 경로상에 A 바로 직전에 n-1개의 edge를 사용해 연결된 B가 있을 것이다.
그럼 시작 vertex로부터 B까지는 최단으로 연결돼있다.(이제 1개 edge만 추가해서 목적지까지 최단으로 가야되니까 당연히 일단 B까지는 최단으로 연결됨)
그럼 B까지 n-1개 edge 사용한게 최단이란 소린데 그럼 B가 n개 edge로 검사할때 갱신될 일은 없고, A까지 n+1개 edge 사용한 경우로 바로 건너뛸 일도 없다.

따라서 위에 나온대로 하더라도 결과는 제대로 나온다.(과정 출력이 우리가 원하게 깔끔하게 안나올뿐..)

6.4.3 All Pairs Shortest Paths (Floyd-Warshall)

모든 vertex pair간의 shortest path를 찾아보자.

negative cost 없으면 dijkstra algorithm을 각각 vertex에 대해 돌려도 구할 순 있다. O(n^3)
Bellman-Ford를 n번 돌려도 되긴 되겠지만 무려 O(n^4)임. 그래서 특화된 알고리즘 사용한다.
얘도 다익스트라 n번 돌린거랑 같은 O(n^3)이긴 하지만 dijkstra보다 constant factor가 작다.
dynamic programming method를 사용해 구한다.

$k$ index 이하의 vertices를 사용해서 i에서 j까지 갈 수 있는 최단거리 2차원 matrix를 $A^k[i][j]$ 라고 하자.( $A^1[i][j]$ 라면 i~j까지 0, 1 vertex통해 갈 수 있는 최단거리)

최종적으로 우리가 원하는건 저런 제한이 없는 모든 pair별 최단거리이므로, $A^{n-1}$ 을 구하면 된다.
$A^{-1}$ 부터 한단계씩 구하는데,
1) $A^{-1}[i][j] = cost[i][j]$
2) $A^k[i][j] = min(A^{k-1}[i][j], A^{k-1}[i][k] + A^{k-1}[k][j]), k \geq 0$
위 단계를 통해 구할 수 있다.(1번 바탕으로 2번 반복)

식 분석
최소 거리는 k index를 가지는 vertex를 통과하는지 안하는지를 기준으로 나뉜다.
$A^k[i][j]$ 가 k를 지나지 않는다면, $A^k[i][j] = A^{k-1}[i][j]$ 이고,
$A^k[i][j]$ 가 k를 지난다면, $A^k[i][j] = A^{k-1}[i][k] + A^{k-1}[k][j]$ 이다.

이해가 잘 안되면 식 그 자체를 잘 보면 된다. 식이 더 이해하기 쉽다.
k 이하의 index 사용한 최단거리가 A^k라고 했으니, 그럼 당연히 A^k는 k를 지나는가 안지나는가 두가지로 나뉨.
그리고 k를 지난다면 당연히 A^k[i][j]는 A^{k-1}[i][k]+A^{k-1}[k][j]이다.
그러므로 A^k는 k를 지나는가를 기준으로 둘로 나뉘어 재귀적으로 정의된다.(2번 식)
우리가 구하고자 하는건 A^v이므로 재귀적 정의에 따라 당연히 A^0부터 구해나가면 된다.
A^k 정의 자체가 저러니까 당연히 A^0부터 차근차근 구하면 A^k가 나오는 것.
2) 식의 우변을 구하면 다음 k값을 구할 수 있는 것이다. 우린 A^{-1}을 알고 있으니 그냥 쭉 구하기만 하면 된다.
(말로 다시 한번 정리: 1번 정점부터 시작해 경유할 수 있는 정점을 하나씩 늘려주며 최단거리를 갱신하는 것이다.)
코드는 그냥 저 식을 옮긴 것에 불과하다.

Implementation
위 분석을 그대로 code로 표현

graph는 adjacency matrix로 표현하고, 존재하지 않는 edge는 큰 수, <i,i> edge는 0으로 표현했다.

void allCosts(int cost[][MAX_VERTICES], int distance[][MAX_VERTICES], int n) {
	int i, j, k;
    
    for (i = 0; i < n; i++)  //A^{-1} 초기화
    	for (j = 0; j < n; j++)
        	distance[i][j] = cost[i][j];
    
    for (k = 0; k < n; k++)
    	for (i = 0; i < n; i++)
        	for (j = 0; j < n; j++)
            	if (distance[i][k] + distance[k][j] < distance[i][j])
                	distance[i][j] = distance[i][k] + distance[k][j];
}

Analysis (allCosts)
matrix data와 무관하게 loop가 돌기 때문에 쉽게 분석된다. O(n^3)
안쪽 for loop가 distance[i][k]나 distance[k][j]가 $\infin$ 이 아니어야 실행되게 하면 시간을 더 줄일 수 있다.

shortest path algorithms 셋다 구현은 되게 간단하다. 적어둘만한 점이 있다면
1. Floyd-Warshall 알고리즘은 위 두개와 다르게 크기를 비교하고 최솟값을 구할때 distance 배열만을 활용한다.
(cost 배열이 없는건 아님, 아래 for문에서 말하는 것)
앞의 두 알고리즘은 하나씩 선택하며 최단거리를 찾는다던가,
edge가 하나씩 추가되며 최단거리를 찾기때문에 distance와 cost(length)의 합으로 비교를하고 계산을 했다.
하지만 이 경우엔 알고리즘 기본 시간 봐도 알 수 있듯이 k를 경유해가기만 하면 어떤 경로든지 찾아야한다.
따라서 둘다 distance 배열을 사용해 계산을 한다.

2. 없는 edge를 INF로 표현했을때, INF 확실히 처리해야하면 확실히 처리하자.
Floyd-Warshall도 INF 배제 안시키면 그 숫자만큼의 cost가 있는 줄 알고 계산이 된다.
INF는 경로가 없다는 뜻이니 조심하자.

6.4.4 Transitive Closure

unweighted directed graph가 있다고 할때, 모든 (i,j) pairs에 대해 path가 존재하는지 확인해보자.
positive path length만 찾는 경우 transitive closure이라 하고,
nonnegative path length를 찾는 경우 reflexive transitive closure이라 한다.

Definition
: The transitive closure matrix, denoted $A^+$ , of a directed graph, G, is a matrix such that $A^+[i][j]=1$ if there is a path of length $>$ 0 from i to j; otherwise, $A^+[i][j]=0$ .

: The reflexive transitive closure matrix, denoted $A^*$ , of a directed graph, G, is a matrix such that $A^*[i][j]=1$ if there is a path of length $\geq$ 0 from i to j; otherwise, $A^*[i][j]=0$ .

둘의 차이는 A[i][i] 경우 밖에 없다.
전자는 i vertex를 포함하는 cycle이 있어야 1이지만,
후자는 무조건 1이다.

Implement
바로 위 Floyd-Warshall algorithm을 이용하여 구할 수 있다.
거리는 모두 1로 세팅하고, 존재하지 않는 edge는 $\infin$ 으로 세팅해서 allCosts 함수를 돌리면 된다.
distance 배열에서 $\infin$ 이 아니면 1로, 맞으면 0으로 해버리면 $A^+$ 를 구할 수 있다.
$A^+$ 에서 모든 $A^+[i][i]$ 를 1로 바꾸면 $A^*$ 를 구할수 있다.

Transitive Closure (undirected graph)

connected components로 쉽게 구할 수 있다.
undirected graph이므로 해당 matrix는 symmetric이고, connected components가 2개 이상이라면 $A^+[i][i]$ 는 0이다.

6.5 ACTIVITY NETWORKS

6.5.1 Activity-on-Vertex(AOV) Networks

너무 간단한 project가 아니라면 activity 라 불리는 여러 subprojectes로 나뉠 수 있다.
예를들어 컴퓨터공학 학사 학위를 받으려면 각 courses를 수료해야한다.
특정 강의는 선행 과목을 듣도록 하고 있다.
directed graph로 이를 나타낼 수 있다.

이를 AOV network라고 한다.

AOV network에서 vertex i에서 j까지의 path가 있다면, i를 j의 predecessor라고 한다.
<i,j> edge가 있다면, i를 j의 immediate predecessor라고 한다.
(successor은 반대)

i.j이고 j.k일때 i.k라면 . 관계는 transitive이다.
x.x인 element가 없다면 irreflexive라고 한다.
transitive이고 irreflexive인 관계를 partial order라고 한다.

AOV network는 보통 불명확하게 표현된다. 위에서도 보면 C4는 C6의 prerequist이지만, <C4,C6> edge는 존재하지 않는다.

Topological order

i가 j의 predecessor라면, i가 j이전에 나오도록 하는 linear ordering이 topological oreder이다.(여러개가 있을 수 있음)

예를들어 위 경우에선 "C1, C2, C4, C5, C3, C6, C7, C8, C10, C13, C12, C14, C15, C11, C9"이 topological order 중 하나다.

graph에서 precedence가 없는 애들부터 빼나가면 topological order로 sort할 수 있다.(outgoing edge도 같이 삭제)
(cycle이 있다면 project는 실행 불가...)

AOV Representation

수행하고자하는 function을 기준으로 data representation을 정해야한다.
Topological sort를 위해 (1)vertex가 predecesor을 가지는지, (2)vertex와 incident edges 삭제 기능을 수행해야 한다.

(1)번은 각 vertices의 immediate predecessors의 개수를 저장하고,
(2)번은 adjacency list로 표현해서 해결한다.

typedef struct node *nodePointer;
typedef struct node {
	int vertex;
    nodePointer link;
} node;

typedef struct {
	int count;
    nodePointer link;
} hdnodes;
hdnodes graph[MAX_VERTICES];

Implementation

graph의 각 elements는 adjacency list의 첫번째 node를 가리킨다.
<i,j>가 들어오면, graph[j].count는 1 증가하고, 이 뒤쪽 link에 붙는다.

count가 0인 vertex는 stack에 추가된다. stack은 count가 0인 field를 link로 활용해 만든다.(0이면 이제 쓸모없으니까)
count 0인 stack에서 빼면서 topological sort를 진행한다.

void topSort(hdnodes graph[], int n) {    //graph 세팅은 다 된걸로 가정하고 진행(adjacency list)
	int i, j, k, top;
    nodePointer ptr;
    
    //stack (with no predecessors)
    top = -1;
    for (i = 0; i < n; i++)
    	if (!graph[i].count) {
        	graph[i].count = top;
            top = i;
        }
    
    for (i = 0; i < n; i++) {
    	if (top == -1) {  //cycle이 있는지 확인. cycle이 있으면 반복문 n만큼 돌기전에 stack 바닥남.
        	fprintf(stderr, "\nNetwork has a cycle. Sort terminate. \n");
            exit(EXIT_FAILURE);
        }
        else {
        	//unstack해서 vertex하나 빼내기
        	j = top;
            top = graph[top].count;
            printf("v%d, ", j);
            
            //unstack했으니 successor들 count 1씩 줄이고, count 0인애 stack에 넣기
            for (ptr = graph[j].link; ptr; ptr = ptr->link) {
            	k = ptr->vertex;
                graph[k].count--;
                if (!graph[k].count) {
                	graph[k].count = top;
                    top = k;
                }
            }
        }
    }
}

Analysis (topSort)
: 처음 for loop는 n만큼 반복하고,
else절내의 for loop는 총 edges수만큼 반복한다.
따라서 O(e + n)이다.

6.5.2 Activity-on-Edge(AOE) Networks

AOV network와 연관된 activity network가 있는데 바로, Activity-on-Edge (AOE) network 이다.

project의 task가 vertex로 표현됐던 AOV에 반해, AOE는 directed edge로 task(activity)를 표현한다.
vertices는 event를 표현한다.(activity가 종료됐는지)

activity(edge)는 연결된 vertex에서 event가 발생하기 전까진 실행될 수 없고,
마찬가지로 event(vertex)도 연결된 activity(edge)가 완료돼야 실행된다.

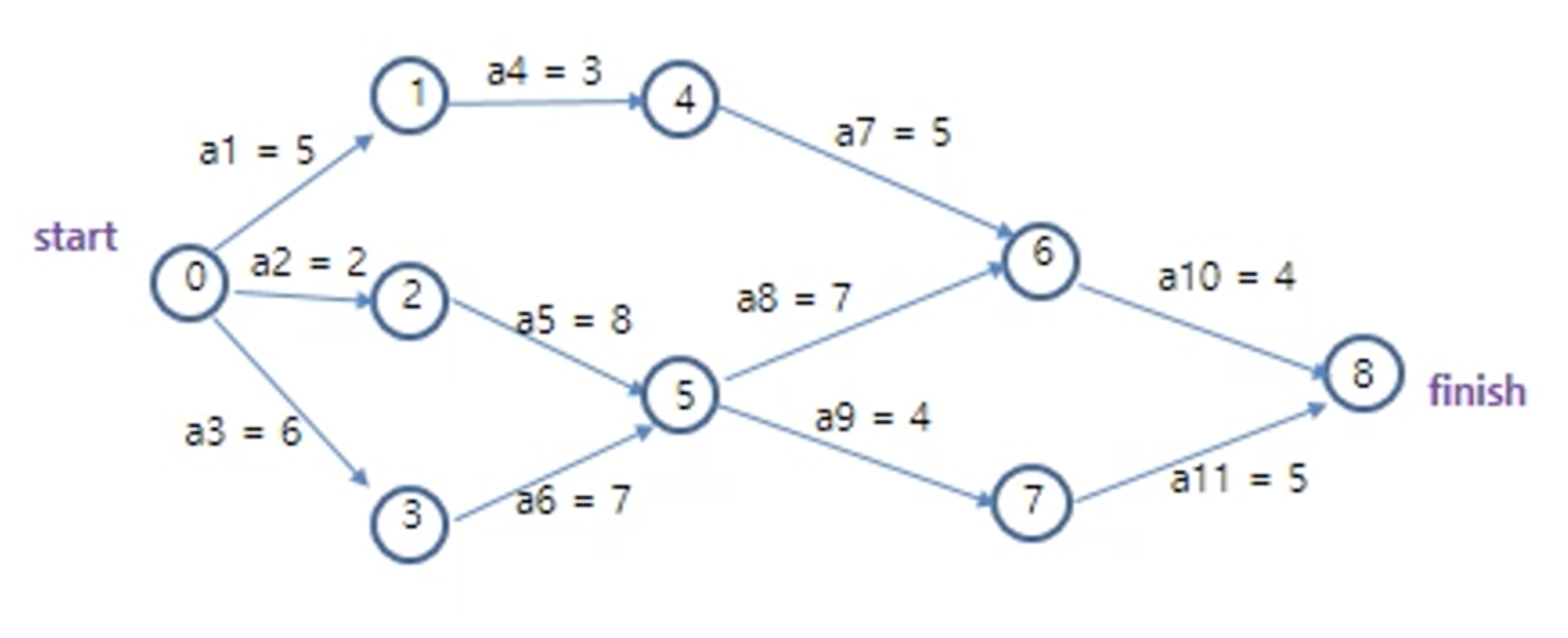
edge(activity)의 숫자는 해당 task를 하는데 걸리는 시간을 의미한다.
(추가적인 ordering constraints가 필요하면, time이 zero인 dummy edge를 추가하면 된다. 예를들어 event(vertex) 4, 5가 실행되기 전에 a8, a9가 실행될 수 없게 하려면 4에서 5로 가는 dummy edge를 추가해준다.)

activities는 parallel(병렬)로 실행되므로, project를 완료하기 위한 최소 시간은 start vertex에서 finish vertex까지의 longest path 길이이다.
이를 critical path라고 한다.(하나가 아니라 여러개 있을 수 있다)
i event(vertex)가 발생하는 earliest time은 시작 vertex에서 i까지의 longest path 길이이다.
activity(edge) $a_i$ 가 발생하는 earlist start time은 e(i)꼴로 나타내진다. 해당 activity가 실행될 수 있는 최소 시간이다. 위 경우 e(8) = e(9) = 13이다.(i자리에 edge가 들어감)
activity $a_i$ 에 대한 latest time인 l(i)도 있는데, 이는 해당 activity가 전체 project 실행 시간에 영향을 안미치려면 최소 얼마 안에 시작돼야하는지이다.(latest time도 project 처음 시작부터의 시간이다.)
(위 그림의 경우 l(5) = 5이다.)
(병렬로 진행중이니, 가장 긴 ciritical path의 끝 시간에 맞출 수 있는 시간을 생각하면 된다.)

e(i) == l(i)라면, critical activities이다.(ciritical path에서 여길 지나감)
l(i) - e(i)를 activity의 criticality라고 한다.(이를 통해 해당 activity가 얼마나 지연돼도 괜찮은지 알 수 있다.)
모든 critical path 위에 있는 activity의 시간을 줄이면 project 시간이 줄어든다. critical path가 하나 이상이라면, 하나의 critical path위에만 있는 activity를 손봤다고해서 전체 시간이 줄어들진 않는다.(ciritical activity가 아니라면 말할 것도 없다.)
(조정 후 critical activity가 바뀔 수 있으니 다시 측정해봐야한다.)

(AOV에도 cost를 추가해서 같은 기능을 할 수 있다.)

AOE에서 `e(i)`와 `l(i)`를 구해보자

6.5.2.1 Calculation of Early Activity Times & 6.5.2.2 Calculation of Late Activity Times

우선 event(vertex)의 earliest event time(ee[j])과 latest event time(le[j])을 구해두면 좋다.
그럼 <p,q> activity $a_i$ 에 대해, e(i) = ee[p]이고, l(i) = le[q] - <p,q>'s cost 이다.

l(i)를 구할때 그냥 le[p]로 바로 구하면 되지않나?
: 위 그림의 5번 vertex를 보면 알 수 있겠지만, 두 activity가 양쪽으로 뻗어나가면 그게 성립이 안된다.
한쪽은 빠른 경로이고 한쪽은 느린 경로일텐데 두 activity가 같은 latest time을 가질 순 없다.
le[p]에서 <p,q> duration만큼 빼주는 것이 정확하다.

ee를 먼저 쭉 구한 후, le는 역순으로 구한다. (그리고 그 값을 바탕으로 activity의 earliest, latest time을 구한다.)

`ee` 구하기

$ee[j]=max(ee[i] + duration\ of\ <i,j>)$ (i는 j의 predecessor)
(보통은 더해 나가는데, 합쳐지는 구간에선 더 큰 값을 작성한다. "병렬로 실행됐을때" 최소 실행 시간을 구하는 것이니 당연히 큰값을 기준으로 한다.)

ee를 구할때는 topological order로 구해주면 좋다. 그러면 predecessor을 먼저 계산하며 차례로 구할 수 있다.
topSort 함수를 수정해 구할 수 있다.

`le` 구하기

$le[n-1] = ee[n-1]$ 과 아래 식을 이용해 구한다.(n-1은 마지막 finish vertex)
$le[j]=min(le[i] - duration\ of\ <j,i>)$ (i는 j의 successor)
(보통은 역순으로 duration을 빼나가는데, 합쳐지는 구간에선 더 작은 값을 작성한다. 최소 시작 시간을 구해야 하므로 당연히 더 긴 route를 뺀것(더 작은 값)을 기준으로 해야한다.)

le는 위에서 ee 구할때 topological order를 반대로 해서 구하면 된다.(뭐 ee구하며 index 순서를 정해두던지..)

이렇게 ee와 le를 다 구하고 나면 e(i)와 l(i)를 구할 수 있다. 그리고 이를 통해 critical activities도 구할 수 있다.

`topSort` 함수는 cycle만 판별할 수 있었다. 다른 문제점도 있는데, 도달할 수 없는 activity이다.
edge가 반대방향으로만 나 있어서 애초에 그 activity로 갈 수 없으면 이것도 문제다.
이건 ee를 위 방식대로 찾아서 start vertex가 아닌데 ee[i] == 0인 지점을 찾으면 된다.

details는 p.324부터... 일단 이정도 핵심 개념만 짚음

지환

이전 포스트

Chapter 5. Trees

다음 포스트