7.1 MOTIVATION

collection of records를 표현하기위해 list란 표현을 사용,
각 records엔 1개 이상의 필드가 있는데 key를 통해 records를 구분한다.
(한 list를 다른 용도로 사용할 수 있기 때문에, 그때마다 key field는 어떤거를 사용하냐에 따라 달라질 수도 있다.)
array 표현법에서 주로 0~n-1이 아니라 1~n으로 나타낼 것이다.(heap sort가 주된 이유)

record를 search하는 방법 1 : 좌-우 or 우-좌로 탐색(sequential search)
key가 a[i]에 있으면 i번의 comparison이 필요
평균 비교횟수 = $(\displaystyle\sum_{1\leq i\leq n}i)/n = (n+1)/2$

정렬돼있다면 더 빨리 할 수 있다.
binary search도 보면 O(n)보다 작은 O(log(n))이다.

하지만 우리가 연명부에서 사람을 찾을땐 이런식으로 안찾는다. 'W'로 시작하는 이름을 찾으려면 그 부분부터 찾으면 된다.
이런 방식을 interpolation search(보간 탐색)이라고 한다.(binary search처럼 막무가내로 반으로 나누는게 아니라, 대충 이쯤 있을 것이라는 가정으로 찾아나간다. 균등하게 정렬돼있는 경우 binary search보다 효율적)

ordered list를 사용하면 computation을 줄일 수 있는 다른 예시를 보자.
본질적으로 같지만 다른 source로 부터 얻은 두개의 list를 비교해보자.
IRS(UnitedStatesInternalRevenueService)에서 자료를 수집하는데, 하나는 고용주로부터 고용인에게 주는 월급을, 하나는 고용인으로부터 고용주에게 받는 월급을 조사한다.
code를 짜보면 알겠지만.. 정렬 후 비교를 진행하는게 더 빠르다.(p.335)

BST같은 자료구조를 굳이 안쓰더라도 sorted array에서 진행하는게 컴퓨터 구조상 더 빠르다.
Why is processing a sorted array faster than processing an unsorted array?

Importance of Sorting

1) searching을 도와줌
2) list matching을 도와줌
3) 이외에 optimization, graph theory, job scheduling 등 다양한 문제에서도 쓰임

아쉽게도 하나의 sorting method가 모든 경우에서 뛰어나진 않기 때문에, 여러 sorting 기법과 어떤 상황에서 그 기법이 좋은지를 배워야한다.

Sorting이란, 아래 조건을 만족하는 특정 permutation($\sigma$) 을 찾는 것이다.
각 record $R_i$의 key value $K_i$에 대해 $K_{\sigma[p]} \leq K_{\sigma[p+1]}$ ($1 \leq p \leq n-1$)
(쉽게말해 key값이 순서대로 배열되도록 하는 순열을 찾으면 그게 sorting이 된 것)
같은 key값을 가지는 경우엔 input에 먼저 나온 놈을 output에도 먼저 나오도록 한다. 이를 stability라고 함.(stability in sorting algorithms)

Sorting methods

1. Internal methods
   : main memory에서 처리가 가능할 정도로 정렬될 list가 작은 경우

2. External methods
   : 큰 lists의 경우

앞으로 별 말 없어도 key로 sorting 된다고 가정

selection sort는 chapter 1에서 정리했었음

---

7.2 INSERTION SORT

sorted sequence에 새로운 record를 넣어가며 정렬한다.
새 record가 들어갈 자리를 비우고(그 자리 뒤로는 한칸씩 밀고) 그냥 넣어버림.

//e를 정렬된 list인 a[1:i]에 넣는다.
void insert(element e, element a[], int i) {  //a는 최소 i+2 공간있어야함
	a[0] = e;
    while (e.key < a[i].key) {
    	a[i+1] = a[i];
        i--;
    }
    a[i+1] = e;
}

//a[1:n]을 정렬(nondecreasing order)
void insertionSort(element a[], int n) {
	int j;
    for (j = 2; j <= n; j++) {
    	element temp = a[j];
        insert(temp, a, j-1);
    }
}

기존 정렬된 배열(길이 n)에 새로운 값을 넣어서 n+1 길이의 정렬된 배열을 만들어내는 원리이다.
a[1]이라는 정렬된 배열에 a[2]를 넣는 것으로부터 시작한다. 이후 a[3], a[4], ...
(그래서 아래 함수의 for문에 j=2부터 넣기 시작하는 것이다.)

insert함수에서 굳이 a[0]에 e를 저장해둘 필요 있나 싶은데,
이를 통해 바로 아래 while문에서 i가 1아래로 내려가는 조건을 따로 test할 필요가 없어진다.
(매번 test하면 그거대로 시간이 좀 걸리긴하겠네)

Analysis(insertionSort)
insert의 complexity는 i+1이고(worst case),
insertionSort는 위 i에 1~(n-1)까지 넣어서 더하면 된다.
O((1 +1)+(2 +1)+...+(n-1 +1)) = O(n^2)
LOO(left out of order), 즉 정렬되지 않은 요소가 k개 있다면 O(kn)이라고 할 수도 있다.

(작은 규모에선 가장?빠르다)

Variations

1. Binary Insertion Sort : insert의 sequential searching을 binary serach로 바구면 시간을 줄일 수 있다.

2. Linked Insertion Sort : linked list로 표현하면, insert한 인자가 들어갈 자리를 만들려고 이동할 필요가 없어져서 빠르게 sort된다.
   하지만 이렇게 한번 표현하면, search할 때 계속 sequential search를 해야돈다는 단점이 있다.

---

7.3 QUICK SORT

C. A. R. Hoare이 개발한 quick sort는 평균적으로 아주 좋은 performance를 보여준다.
(이 책에 나오는걸로 봤을땐 평균적으로 제일 좋다고 함)

우선 pivot이라는 기준을 잡고, pivot의 왼쪽에는 pivot보다 작거나 같은 값들을, pivot의 오른쪽에는 pivot보다 크거나 같은 값들을 위치시킨다.
이를 반복한다.(재귀로 주로 하네)

Implement

pivot은 왼쪽끝(a[left])으로 잡고, [왼쪽끝+1]과 [오른쪽끝]에서 하나씩 보면서 오다가 바꿔야되면 위치를 바꾼다.
그러면 마지막에 꼭 절반 위치가 아니더라도 특정 지점 기준으로 왼쪽은 pivot보다 작거나 같은 값, 오른쪽은 pivot보다 크거나 같은 값이 온다.
왼쪽부분의 제일 오른쪽 값과 pivot을 바꿔주면 된다.(pivot은 a[left]로 잡았으니까)

//a[1:n]을 정렬한다.
void quickSort(element a[], int left, int right) {
	int pivot, i, j;
    element temp;  //위치 변경 위한 임시저장공간
    
    if (left < right) {
    	i = left; j = right + 1;
        pivot = a[left].key;
        do {
        	do i++; while (a[i].key < pivot);
            do j--; while (a[j].key > pivot);
            if (i < j) SWAP(a[i], a[j], temp);
        } while (i < j);
        SWAP(a[left], a[j], temp);  //pivot을 분할 지점으로 옮겨주기
        quickSort(a, left, j-1);
        quickSort(a, j+1, right);
    }
}

조건 잘 따져가며 머리로만 하려하지말고 그리거나 적어보고 그걸 그대로 옮기자.
quick 제대로 이해하면 do-while로 먼저 접근하는게 빠르다는걸 알 수 있음.
난 for이랑 while로 짜니까 조건 따지기가 좀 더 귀찮아짐.
직접 짜볼때 제대로 안됐던게, 첫번째 SWAP에서 if로 판단하고 SWAP해야된다는거..
i와 j가 역전돼있으면 pivot 위치시켜야된다.
바깥 do while문 i<j가 아니라 i=j일때도 한번 더 돌려서 j가 아예 pivot보다 작은 영역으로,
i보다 확실히 작게 해야되지 않나 라고 생각할 수도 있는데,
둘이 역전할때쯤에 안쪽 do while문 돌고나면 i=j가 될 수가 없다.
안쪽 dowhile문 둘 다 돌고나면 역전되거나 안되거나 둘중하나다.(안되면 아직 이 단계에서 sort 덜 끝났단 소리)

Analysis(quickSort)
최악의 경우(list가 이미 정렬된 경우) O(n^2)이다.
평균의 경우 O(n log(n))인데, 이를 증명해보자.

$T_{avg}(n)$은 quickSort를 이용하여 n개의 records를 정렬하는데 걸리는 시간이다.
$T_{avg}(n) \leq knlog_en$ 인 k가 존재함을 증명해보자. (n>=2로 가정)
quickSort 실행 후 두개의 sublists size는 pivot위치가 j일때 j-1과 n-j이다.
따라서 $T_{avg}(n)$은 $T_{avg}(j-1) + T_{avg}(n-j) + cn$이다.(cn은 함수 남은 부분 실행 시간)
이때 j의 위치는 1 ~ n 중 같은 확률로 올 수 있다.
따라서 $T_{avg}(n) \leq cn + \frac{\displaystyle\sum_{j=1}^{n}(T_{avg}(j-1)+T_{avg}(n-j))}{n})=cn+2\frac{\displaystyle\sum_{j=0}^{n-1}T_{avg}(j)}{n}$
그리고 아래 여차저차한 과정을 통해 증명함.(p.342~343)

(인터넷에 보니) 같은 O(nlogn)이더라도 quick이 가장 빠르다고 함

space complexity
insertion sort에선 저장공간 한칸이 더 필요했는데, quick sort는 recursion을 위한 stack space가 필요하다.
평균적으론 log(n) 만큼만 recursion이 일어나면 되지만, 최악의 경우 O(n)이다.
sublist가 2보다 작은 경우 stack에 넣지 않거나, 작은 sublist를 먼저 계산하는 방식으로 stack space를 줄일 수 있다.

Variation

• Quick Sort using a median-of-three
  위 버전처럼 제일 왼쪽 값을 pivot으로 고르기보다, sublist의 (1)처음 값과 (2)중앙 값과 (3)마지막 값의 중앙값을 고르면 더 낫다.
  예를들어 1, 5, 2 였다면, 2를 pivot으로 선택하는 것이다.

해당 pivot이 적어도 최대/최소는 아니므로 어느정도 수준으로 time complexity가 유지된다.
(모든 pivot이 해당 sublist에서 최대/최소라면 worst case이다. 예를들어 위에 말했듯이 이미 정렬돼있으면 제일 왼쪽값을 pivot으로 했을때 총 n번 recursion 일어남. worst case인 O(n^2)이 된다.)

---

7.4 HOW FAST CAN WE SORT?

insertion, quick 모두 worst case에서 O(n^2)이었다. (selection도 O(n^2)임)

sorting하는데 있어서 best computing time은 얼마일까??
sorting할때 key에 관해 할 수 있는 operation이 comparison과 interchange 뿐이라면 O(nlog(n))이 최선이다.

증명

위와 같은 tree를 decision tree라고 한다. 위 tree는 insertion sort의 decision tree이다.
n개를 sorting할때 n!개의 leaves가 있으므로, 3개의 records에 대해 유효한 sorting algorithm이다.

여기서 tree의 높이를 실행시간으로 볼 수 있는데, 높이를 k, records 수를 n이라고 해보자.
leaf 수는 최대 $2^{k-1}$개이거나, 최소 $n!$개이다.
따라서 높이 k의 최솟값은 $\log_2 n!+1$이다.

$n! = n(n-1)(n-2)...3*2*1 \geq n(n-1)(n-2)...n/2 \geq (n/2)^{(n/2)}$
즉, $\log_2(n!) \geq (n/2)\log_2(n/2) = Ω(n\log n)$
(comparison-based sorting method의 평균 complexity)

---

7.5 MERGE SORT

7.5.1 Merging

2개 sorted list를 합쳐서 하나의 sorted list로 만들어보자.
다항식 덧셈 할때처럼 크기비교해가며 적다가, 마지막에 남은놈들쭉 적어주면 된다.

initList[i:m]과 inintList[m+1:n]을 합쳐서 mergedList[i:n]을 만든다.
(mergedList만들때 부자연스럽게 i index부터 시작하는 이유는 merge sort할때 써먹으려고)

viod merge(element initList[], element mergedList[], int i, int m, int n) {
	int j, k, t;
    j = m+1;  //두번째 sublist를 위한 index
    k = i;    //merged list를 위한 index
    
    while (i <= m && j <= n) {
    	if (initList[i].key <= initList[j].key)
        	mergedList[k++] = initList[i++];
        else
        	mergedList[k++] = initList[j++];
    }
    if (i > m)
    	for (t = j; t <= n; t++)
        	mergedList[t] = initList[t];
    else
    	for (t = i; t <= m; t++)
        	mergedList[k+t-i] = initList[t];
}

Analysis (merge)
O(n-i+1)

array말고 linked list로 표현하면, sorted array 추가 공간이 필요하진 않지만 link를 위한 공간이 추가로 필요하다.

7.5.2 Iterative Merge Sort

input list의 각 sublist를 크기가 1로 정렬된 list로 본다.
양옆으로 merge를 여러번 진행하며 sorting한다. (sublist 개수 n인 list 한번 merge하면 sublist 개수는 n/2이 된다.)

Implement

mergePass 함수가 진행될때마다 한번의 merge가 일어난다. 이를 mergeSort가 여러번 호출하여 merge sort를 한다.(merge를 mergePass가 호출, mergePass를 mergeSort가 호출)

//initList의 각 sublist가 mergedList로 merge된다. n은 element개수이고, s는 sorted segment의 size이다.
void mergePass(element initList[], element mergedList[], int n, int s) {
	int i, j;
    for (i = 1; i <= (n - 2*s + 1); i += (2*s))  //딱 맞게 2s 범위 merge 할 수 있는 만큼만 한다.
    	merge(initList, mergedList, i, i+s-1, i+2*s-1);
    if (i+s-1 < n)  //뒤에 남는 부분이 서로 다른 sublist인지 확인, 같은 sublist라면 그냥 그대로 두면 된다. 
    	merge(initList, mergedList, i, i+s-1, n);
    else  //모두 같은 sublist에 속하니 그냥 그대로 옮긴다.
    	for (j = i; j <= n; j++)
        	mergedList[j] = initList[j];
}

딱 s로 나누어 떨어지면 좋지만, 그렇지 않을 수 있다.
2s크기씩 merge 시키다가 뒤에 남은부분을 차리하는게 code 아랫부분이다.

//a[1:n] sort
void mergeSort(element a[], int n) {
	int s = 1;   //segment size
    element extra[MAX_SIZE];  //mergedList 저장하기 위해 사용(반대로도 사용)
    
    while (s<n) {
    	mergePass(a, extra, n, s);
        s *= 2;
        mergePass(extra, a, n, s);
        s *= 2;
    }
}

Analysis (mergeSort)
$n \geq 2^{i-1}$ (n은 총 element 개수, i는 mergePass 호출 횟수)
따라서 $⌈\log_2n⌉$만큼 mergePass는 호출된다.
merge가 O(n)이었으니, O($n\log n$)이다.
(추가로, stable sorting algorithm이다.)

mergePass내의 for문들이 다 합쳐져야 총 O(n)이 되는거다. segments를 merge에 보내는거니까.
그래서 그냥 O(n)으로 사용한 것.

함수 3개 사용했고, 특히 mergePass에서 범위 처리 잘해야 제대로 작동함.

7.5.3 Recursive Merge Sort

반으로 잘라가며 recursive하게 merge sort를 진행한다.
left~⌊(left+right)/2⌋와 ⌊(left+right)/2⌋+1~right로 나누며 진행한다.

merge에서처럼 다른 array에 복사하지 않기위해, link[1:n] 배열을 사용한다.
(link[i]는 sorted sublist에서 i다음에 올 element를 가리킨다. link[0]이면 뒤에 암것도 없단 뜻.)
그래서 sorting된 결과로는 link로 연결된 chain이 나오는데, 이 배열대로 진짜 값들을 재배열 해야한다.(재배열은 Section 7.8에 나옴)

Implement

merge 함수가 link를 이용하도록 다시 만든다.

//start1과 start2, 두개의 chain을 merge하고, merge된 chain의 시작 지점을 반환하는 함수
int listMerge(element a[], int link[], int start1, int start2) {
	//link[0]을 merge되는 결과 list의 header처럼 사용한다.
	int last1, last2, lastResult = 0;  //last로 link를 따라간다. lastResult는 merge list의 마지막을 가리킴
    
    for (last1 = start1, last2 = start2; last1 && last2;)
    	if (a[last1] <= a[last2]) {
        	link[lastResult] = last1;
            lastResult = last1;
            last1 = link[last1];
        }
        else {
        	link[lastResult] = last2;
            lastResult = last2;
            last2 = link[last2];
        }
        
    //남은 부분 chain에 붙이기
    if (last1==0) link[lastResult] = last2;
    else link[lastResult] = last1;
    
    return link[0];
}

위 함수를 이용하여 mergeSort를 reculsive하게 진행한다.
처음은 모두 size 1인 sublists이니 link[]는 0으로 초기화한다.

//merge 후 chain의 첫번째 index를 반환한다.
int rmergeSort(element a[], int link[], int left, int right) {
	if (left >= right) return left;
    int mid = (left + right) / 2;
    return listMerge(a, link, rmergeSort(a, link, left, mid), rmergeSort(a, link, mid+1, right));
}

Analysis (rmergeSort)
O($n\log n)$
추가로 얘도 stable하다.

왼쪽 절반 sort, 오른쪽 절반 sort를 재귀적으로 구현
서로 다른 두 함수로 구현한게 좀 봐둘만 한거같네
left>=right일때 left 반환하도록한건 재귀 끝에서 종료되는 조건인데,
rmergeSort(a, link, 8, 9)나 rmergeSort(a, link, 1, 2)가 호출됐다고 생각해보면 된다. (int라 어차피 truncated되면 left가 right보다 커질 순 없는데 왜 저렇게했지..)

Variation

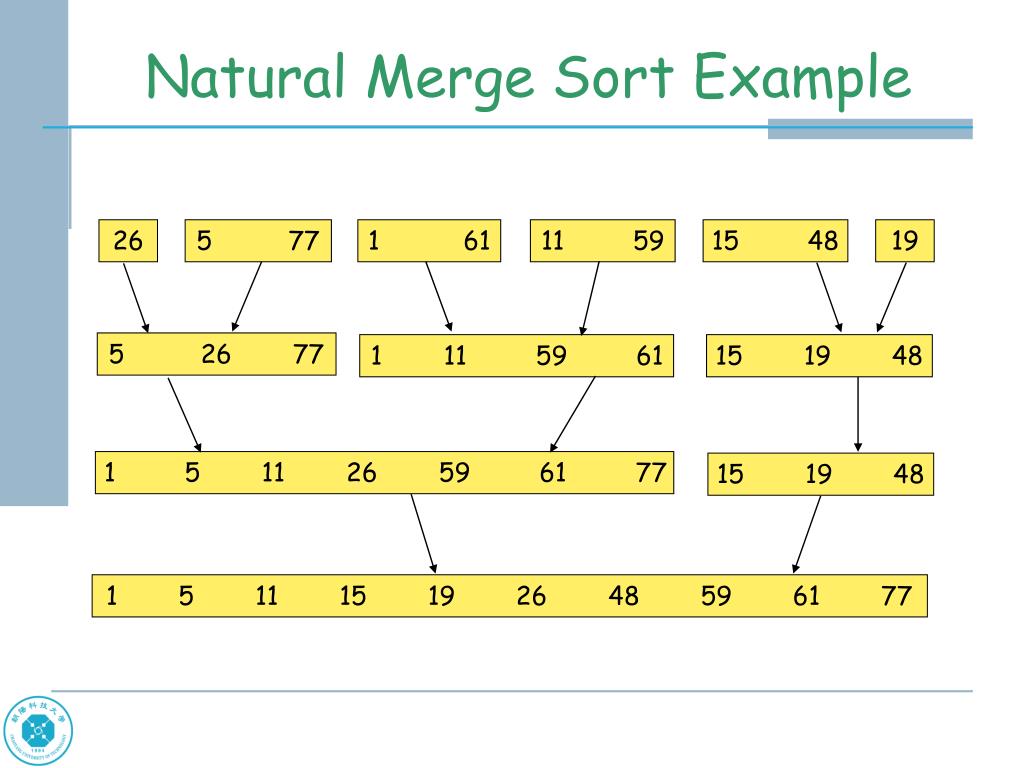
• Natural Merge Sort
  위에선 인위적으로 모든 각 elements를 sublists로 봤지만, input list에서 이미 정렬된 부분은 그걸 sublist로 볼 수 있다.

---

7.6 HEAP SORT

merge sort는 worst나 average 모두 O($n\log n$)로 빠른 편이지만, records수에 비례한 추가 공간이 필요하다.
반면 Heap Sort는 고정된 추가 공간이 필요한데, O($n\log n$)이다.(merge보다 조금 더 느리긴 함)

max heap(chapter5)을 사용한다.(inserting, deletion 함수는 그대로 사용하지 않고 여기에 맞게 다른 방식으로 max heap 다룸)
max heap만들때, 그냥 empty heap에 records 하나씩 넣는 것보다 빨리 하기 위해 adjust 함수를 사용한다.
adjust 함수는 root를 기준으로 left subtree와 right subtree가 max heap임을 가정하고 전체 tree가 max heap이 되도록 root가 제 자리를 찾아가게 조정하는 함수이다.
(그래서 전체 tree를 adjust하려면 제일 아래 subtree부터 차근차근 adjust해야함)
(max heap insert할때는 끝에 넣어서 비교하며 올라갔는데, 여기선 작은 subtree들을 max heap으로 만들어가는 방식이다. 하나만 insert하면 전자의 방법을 사용하지만, 지금은 아예 max heap을 만들어야되는 상황이라 좀 다른듯)
(root deletion하고 adjusting하는거랑 같네)

heap은 array로 표현한다.
정렬하고자 하는 배열(a[1:n])을 입력하면 사실상 binary tree를 입력하는 것으로 보고, 그걸 max heap이 되도록 adjusting하며 정렬을 진행한다.

순서

1~n 범위 adjust완료하고나면(==max heap 만들고 나면) root인 [1]에 최대값이 있다.
그럼 (정렬하면 제일 끝에 max값이 있어야하니까) 1과 끝 위치를 바꿔주고, 1~n-1 범위를 다시 adjust한다.
(1과 n 바꾼 뒤의 adjust부터는 adjust함수를 한번만 호출해도 된다. 왜냐하면 root 기준 왼쪽 오른쪽 subtree 모두 max heap이니까)
이렇게 쭉~

Implementation

void adjust(element a[], int root, int n) {
	int child, rootkey;
    element temp;
    temp = a[root];
    rootkey = a[root].key;
    child = 2*root;    //left child
    
    while (child <= n) {
    	if ((child < n ) && (a[child].key < a[child+1].key))
        	child++;  //child 중 더 큰 애를 기준으로 한다.
        
        if (rootkey > a[child].key)  //두 child 모두 parent보다 작다면 그대로 가주면 됨
        	break;
        else {  //아니라면 root는 해당 child's subtree에서 다시 비교
        	a[child/2] = a[child];
            child *= 2;
        }
    }
    a[child/2] = temp;
}

adjusting 할때 중요한 점이 (deleting하고 조정할때도 마찬가지) root와 두 children 총 3개를 비교해서 제일 큰 놈이 올라와야 한다는 것이다.
두 child가 둘 다 parent보다 크다고 해서 아무나 올려보내면 되는게 아니라 가장 큰 놈이 올라와야 max heap이 성립한다.

//a[1:n] 정렬
void heapSort(element a[], int n) {
	int i, j;
    element temp;
    
    //make initial max heap
    for (i = n/2; i > 0; i--)  //가장 작은 subtree의 root는 n/2 위치에 있다
    	adjust(a, i, n);
        
    for (i = n-1; i > 0; i--) {
    	SWAP(a[1], a[i+1], temp);
        adjust(a, 1, i);
    }
}

Analysis (heapSort)
tree에서 node 수를 $n$, level을 $k$라고 하자. (level이 $k$이니, $2^{k-1} \leq n < 2^k$)
첫번째 for loop에서 child를 가진 node를 모두 한번씩은 호출한다.
따라서 첫번째 for문의 time은 $number\ of\ nodes \times maximum\ distance\ the\ node\ can\ move$를 넘지 않는다.
$\displaystyle\sum_{1\leq i\leq k}2^{i-1}(k-i) = \displaystyle\sum_{1\leq i\leq k-1}2^{k-i-1}i \leq n\displaystyle\sum_{1\leq i\leq k-1}i/2^{i} < 2n = O(n)$

두번째 for loop에서 adjust 한번에 $⌈\log_2(n+1)⌉$, SWAP은 n-1만큼 걸린다. 총 n-1번 호출되니, $O(n\log n)$이다.

최종적으로 time complexity는 $O(n\log n)$

space는 (자잘한 변수 제외하면) SWAP할때 필요한 temp가 전부이다.

---

7.7 SORTING ON SEVERAL KEYS

한 record의 key가 하나가 아니라 여러개일때의 정렬을 알아보자.
$(K_i^1, K_i^2, K_i^r)\leq (K_j^1, K_j^2, K_j^r)$ 일때, $R_1, R_2, R_3, ..., R_n$이 $K^1, K^2, ..., K^r$의 관점에서 정렬됐다고 한다.
($K^1$이 most significant key이고, $K^r$은 least significant key이다.)
(ex. 트럼프카드 정렬)

multiple keys를 다루는 유명한 두가지 정렬 방법이 있다.
1) most-significant-digit-first(MSD) sort
: most significant key $K^1$부터 key 하나씩을 기준으로 정렬한다. 그럼 같은 key값을 가지는 "piles"가 나오는데, 얘네는 두번째 key인 $K^2$를 기준으로 정렬한다. 이를 반복한다.
2) least-significant-digit-first(LSD) sort
: MSD sort보다 좀 더 자연스러운 방법이다. 우선 least significant key로 정렬을 한다. 그럼 몇몇 piles이 생길건데, 이 전체 list에 stable sorting을 진행하면, 쭉 정렬이된다.

둘을 비교해보자면 LSD가 더 간단하다. MSD는 piles을 독립적으로 정렬해야되는데 반해 LSD는 stable sorting이란것만 보장되면 piles과 subpiles을 독립적으로 정렬할 필요가 없다.
(LSD면 그냥 stable하게 같은 종류끼리 모으기만 하면 됨)

MSD와 LSD는 순서에 관한 것이지, 방법에 관한 것이 아니다.
예를들어 우리가 손으로 트럼프 카드를 정렬한다면 MSD를 사용할 것이다. 우선 모양별로 bin sort(4개의 bins에 맞게 배치시킨다)를 진행하고, 같은 모양 내에서 정렬할때는 insertion sort와 비슷한 algorithm으로 정렬할 것이다.

key가 하나 뿐이어도 여러개의 keys로 구성됐다고 가정하고 MSD or LSD를 사용할 수 있다.
예를들어 숫자를 정렬할때, 일의자리 십의자리 백의자리 등으로 key를 나눠서 볼 수 있다.

radixSort

radix r로 key를 decompose해서 정렬한다.
r이 10이라면 위에서 말했던대로 일의자리 십의자리 이렇게 나누는거고..
총 r개의 bins(piles)가 필요하다.
각 bin은 queue로 표현된다. radix가 i인 bin은 front[i]와 rear[i]가 처음과 끝을 가리키고, bin내의 records는 chain으로 연결된다.(아래 code에선 link[] 사용)
bin마다 모으는 식으로 정렬을 하고, bin끼리 다시 이어붙인다.

주의 : stable sort여야한다. stable이 아니면 의미도 없을 뿐더러 작동도 제대로 안한다.(혼자 짜다가 왤케 이상하지 했더니 stable이 아니었네.. link를 편하게 삽입하려고 거꾸로 넣고있었음)
그리고 bin은 queue로 구현하는게 훨씬 쉽다.. front rear 배열만 있으면 됨. singly linked list로 하니까 복잡하네 연결할때마다 끝부분 찾아야되고
또 이렇게 link로 정렬하려니까 좀 헷갈린다. link로 정렬할때는 본래 값 ex.a[i] 같은건 잘 쓸일이 없다. 이 점도 주의해서 하자.

//a[1:n] 정렬
//자릿수는 d이고, radix는 r이다. digit(a[i], j, r)은 radix-r기준 j번째 digit을 반환

int radixSort(element a[], int link[], int d, int r, int n) {
	int front[r], rear[r];  //queue
    int i, bin, current, first, last;
    
    //create initial link(그냥 쭉 연결)
    first = 1;
    for (i = 1; i < n; i++) link[i] = i+1;
    link[n] = 0;
    
    for (i = d-1; i >= 0; i--) {  //digit 함수를 0번째자리부터 보게 만든듯
    	for (bin = 0; bin < r; bin++)
        	front[bin] = 0;  //bin(queue)초기화
        
        //bin sort 순서대로(stable) bin끼리 모은다
        for (current = first; current; current = link[current]) {
        	bin = digit(a[current], i, r);
            if (front[bin] == 0)
            	front[bin] = current;
            else
            	link[rear[bin]] = current;
            rear[bin] = current;
        }
        
        //bin끼리 연결한다.
        for (bin = 0; !front[bin]; bin++);  //우선 들어있는 bin을 찾아 처음에 넣어준다
        first = front[bin]; last = rear[bin];
        
        for (bin++; bin < r; bin++)
        	if (front[bin]) {
            	link[last] = front[bin];
                last = rear[bin];
            }
        link[last] = 0;
    }
    return first;
}

Analysis (radixSort)
: 한단계에 $O(n+r)$ time인데, 총 $d$번 일어난다.
따라서 total time은 $O(d(n+r))$이다.

$d$는 $r$과 최대 key값에 의해 결정된다. 따라서 $r$(radix)가 달라지면 computing time도 달라진다.

digit 반환 함수
위 radixSort랑 호환은 안되는데, n번째 자리 반환하는 함수 간단하게 짜봄.

int digit(int number, int digit_n) {  //'digit_n은 몇번째 digit을 구할것인가'이다. 1번째가 1의자리
    int denom = 1;
    
    for (int p = 1; p < digit_n; p++)
        denom *= 10;
    number /= denom;   //int 나누기하면 truncated되는 것 이용, 그러면 해당 자릿수 밑으론 다 날아감.
    return (number % 10);  //구하고자 하는게 이제 1의 자리에 있으니 10으로 나눈 나머지가 답
}

---

7.8 LIST AND TABLE SORTS

radix sort나 recursive merge sort 말고는 data movement가 꽤 많이 필요했다.
data양이 많을 경우 data movement로 시간이 많이 소요될 수 있다.

insertion sort나 iterative merge sort는 linked list를 사용해도 되지만,
결국 물리적 공간을 완전히 이동해야 하는 경우가 있다.(물론 나중에 옮기더라도 무조건 옮기며 정렬하는 것보단 시간이 절약되긴 한다.)

우선 link로 연결을 수정해 정렬한 경우, 물리적으로 재배치하는 방법인 list sort와
값의 위치 값을 이용해 정렬한 경우, 물리적으로 재배치하는 방법인 table sort에 대해 알아보자.

List Sort

Implement 1

$R_1$ 위치의 값과 $R_{first}$ 위치의 값을 바꾸고, $R_1$을 가리키던 link 등 link들이 바뀐 position을 가리키도록 수정하면 된다.
이 과정을 반복한다.
문제는 singly linked list에서는 predecessor을 모른다는 것이다.

그래서 signly를 doubly linked list로 바꾼 후 위 과정을 진행하자.

//radixSort, recursive merge sort에서처럼 배열로 link 표현했다고 가정
//물론 a[]는 linka를 따라 이미 정렬됐다고 가정
void listSort1(element a[], int linka[], int n, int first) {  //a는 실제 배열, first는 시작 index
	int linkb[MAX_SIZE];  //predecessor을 가리키는 link 배열
    int i, current, prev = 0;
    element temp;
    
    //make doubly linked list
    for (current = first; current; current = linka[current]) {
    	linkb[current] = prev;
        prev = current;
    }
    
    //실제 순서에 맞게 이동, first를 이용해 쭉 훑으며 간다. 값만 이동하지말고 link도 올바르게 변경해준다.
    for (i = 1; i < n; i++) {
    	if (first != i) {  //둘이 같으면 바꿀 필요 없음
          if (linka[i])
          	linkb[linka[i]] = first;
          linka[linkb[i]] = first;
          SWAP(a[i], a[first], temp);  //우선 값 바꾸고, 아래로는 link들도 위치 바뀐대로 바꿔준다.
          SWAP(linka[i], linka[first], temp);  //temp 자료형 다르지않나
          SWAP(linkb[i], linkb[first], temp);
        }
        first = linka[i];
    }
}

각 element마다 앞뒤로 나가는 link두개, 앞뒤에서 들어오는 link 두개씩 있다.
first는 이제 제자리로 찾아 들어갈 것이기 때문에 본인으로 들어오는 link 두개는 조정해줄 필요가 없다.
수정해도 의미(쓸모)가 없다.
linkb[first]는 제자리에 먼저 들어와있을 것이기 때문에 linka[linkb[first]]는 수정할 필요가 없고,
linka[first]는 

Analysis (listSort1)
doubly linked list 만드는데 $O(n)$
아래 for문은 실행마다 3개의 records를 move한다, 한 record 크기가 m이라면, 총 $O(mn)$이다.
(worst case : 3(n-1) move 발생)

Implementation 1-1

for (i = 1; i <= n; i++) {
        next = linka[first];  //다음 갈 곳 저장
    	if (first != i) {  //둘이 같으면 바꿀 필요 없음
    	    if (linka[i])
                linkb[linka[i]] = first;  //뒷쪽에서 위치가 바뀔 가능성 존재하므로 link 유지해야함
    	    if (linka[first] == i)  next = first;  //다음 갈 곳이 바뀌는 위치면 따로 저장
            linka[linkb[i]] = first;
            SWAP(a[i], a[first], temp);
            linka[first] = linka[i];
            linkb[first] = linkb[i];
        }
        first = next;
    }

나는 위 listSort1의 아래쪽 for문을 이렇게 구현해봤다.(나머지 뭐 doubly linked list만들고 하는건 똑같이 함)
우리가 doubly linked list로 만드는 이유는, 값을 swap하고나면 그 다음 값을 찾아 갈 수가 없기때문에 이전 link를 수정해줄 필요가 있어서였다.
그럼 first가 본래 위치인 i로 간다면, 제자리로 정렬된 node는 link가 어떻게되든 상관없다. 다시 그곳(index가 i 이하인 곳)으로 갈 일도 없고, 정렬이 우리 목적이니..
그럼 굳이 linka, linkb 다 SWAP 할 필요없이 필요한 값들만 유지하면 되지않나 싶어서 이렇게도 해봤는데 잘 돌아간다.
index가 i이상인 곳은 doubly linked list가 완전히 유지되어 있어야 하므로 위와 같이 그 부분만 신경써서 값을 유지한다.
그리고 다음으로 갈 위치는 미리 저장해뒀다가 SWAP 종료 후 따라가는데, 다음으로 갈 위치가 서로 바뀌는 위치일 수 있으니 그건 따로 처리해준다.
main은 i위치에 있던 값에 대해서만 link 4개를 모두 유지해준다.
나가는 link인 linka[i], linkb[i], 들어오는 link인 linka[linkb[i]], linkb[linka[i]] 네개도 잘 따라다니게 유지시켜 주는 것이다.

근데 이것도 확실히 검증된건 아니니까 그냥 listSort2 잘 배워서 써먹자. 어차피 더 효율적이니까.

Implementation 2

이해하면 listSort1보다 쉬움, 그리고 시간/공간 이득, 얘 쓰자 (솔직히 listSort1보다 더 잘 이해되네)
M. D. MacLaren이 제시한 방법대로 위 code 수정하자, 추가 link fields가 필요없음
: 위에서 link를 모두 수정해준 이유는, link 값은 그대로 놔두고 값들만 띡띡 바꾸면 다음 순서의 값을 찾다가 이미 값이 바뀐 위치로 갈 수도 있기 때문이다.(1 다음 값인 2가 여기있대서 왔는데 다른 값이 있을 수 있다)
이렇게 이미 바뀐 위치로 가는 경우는 i 미만인 위치로 가는 경우 밖에 없다.(왜냐하면 바뀌었다는건 본인 위치에 정렬됐다는거니까)
따라서 memory상에서의 정렬을 위해 두 위치(i, first)의 값을 바꿀때, i위치의 link를 수정해서 "원래 여기(a[i]) 있던 애는 여기(link[i])에 있어"라고 알려주기만 하면 문제가 해결된다. "아 2찾아서 왔니? 2는 저기에 있어"
==> link[i] = first;

추가로 해야할 작업은, 바뀐 위치만 알려줄게 아니라 link도 같이 가져가야한다.
무슨 말이냐면, 어떤 값 a를 찾으러 왔는데 여기에 없어서 a의 바뀐 위치를 알았다면 그 다음으론 a 다음 값의 위치도 알아야 한다는 것이다.
그 다음 위치는 원래 a가 있던 위치의 link에 저장돼있으니, 둘을 바꿀때 그 정보도 가져와야한다.
==> link[first] = link[i];

두 값을 바꿀때 위의 작업(여기 있던 애가 어디로 이동했는지 알려주고 + 둘을 바꿀때 그 다음 값의 위치 정보도 가져온다)만 추가로 진행해준다면,
다음 순서의 값을 찾았는데 i 미만의 위치일 경우(== 값이 바뀐 경우) i보다 큰 위치로 갈때까지(== 값이 바뀐 경우가 아닐때까지) link를 타고 가주면 된다.
==> while (first < i) first = link[first];

vod listSort2(element a[], int link[], int n, int first) {
	int i, next;
    element temp;
    
    for (i = 1; i < n; i++) {
    	while (first < i) first = link[first];
        next = link[first];
        if (first != i) {
        	SWAP(a[i], a[first], temp);
            link[first] = link[i];
            link[i] = first;   //이게 맞는 순서, 위에 설명할땐 잘 알아들으라고 반대로 설명한거임
        }
        first = q;
    }
}

Analysis (listSort2)
listSort1이랑 같다. $O(mn)$

while문에선 2번이상 거치는 node는 없으므로 while loop의 total time은 O(n)이다.(for문 실행될때마다가 아니라 전체 program 실행 중에 n번이상 안돌아감)

Analysis (listSort1 & listSort2)

listSort2가 공간적으로나 시간적으로나 listSort1보다 낫다.

quick 이나 heap sort에서는 list sort가 적합하지 않다.
(listSort는 링크로만 정렬했을때 물리적 공간을 이동하는 것인데, heap 같은 경우 sequential representation이 애초에 필수이므로)

이런 sorting 방식에선 auxiliary table(t)를 사용할 수 있다.(radixSort같은데서도 쓸 수 있음)
t는 원래 배열에서 값을 복사한게아니라 위치를 가져온 복사본인 셈이다.(heap sort같은거 물리적으로 data 이동할때, t에서만 값전체가 아니라 위치정보만 이동하면 소요 시간 적게 할 수 있을 듯)
t[i] = i;로 처음엔 초기화 된다.(그게 처음 위치니까)
$a[t[1]], a[t[2]], ..., a[t[n]]$ --> Sorting 결과
(a[1]=3이라면 1만 복사해와서 sort할때 움직이는 거임. 여기선 고작 3이지만 다른 큰 data면 이 방법이 더 효율적)

Table Sort

모든 순열(permutation)은 disjoint cycles로 이뤄진다는 사실을 사용해 해결한다.
위 처럼 t 배열을 이용해 정렬한 경우 t의 값들 또한 순열이므로 여러 disjoint cycles로 나뉜다.
여기서 말하는 cycle이란,
$i, t[i], t[t[i]], ..., t^k[i]$로 쭉 갔을때 $t^k[i]$가 $i$가 된다면 cycle이라고 한다. ($t^j[i] = t[t^{j-1}[i]]$, $t^0=i$)
초기 t[i] == i였는데, 정렬 할때 이 t의 값들이 서로 바뀌면서 정렬되므로, 바뀐 값들끼린 cycle을 형성한다.
(예시 그림 하나 그려서 두개 세개 네개 바꿔보면 cycle 이루는거 금방 이해됨.)

이를 이용해서 --> 물리적으로 정렬
$t[i] == i$인 경우, 이동할 필요 X
아니라면, $i$ 위치의 값은 temp에 임시로 저장 후, $t[i]$ 위치의 값을 $i$로 옮긴다.
그리고 $t[t[i]]$ 위치의 값을 $t[i]$로 옮긴다.
cycle이 종료될때까지 위 과정을 반복한다. 그리고 마지막 지점에 temp의 값을 옮겨준다.

//a[1:n] 물리적으로 정렬
void tableSort(element a[], int n, int t[]) {  //물론 t로 이미 정렬됐다고 가정
	int i, current, next;
    element temp;
    
    for (i = 1; i < n; i++) {
    	if (t[i] != i) {  //같다면 옮길필요 X
        	temp = a[i];
            current = i;
            do {
            	next = t[current];
            	a[current] = a[next];
                t[current] = current;  //증요.원래 위치에 있어야 할 애를 원래 위치(current)로 옮겨왔으니 t값도 바꿔준다.
                current = next;   //cycle 다음 순서로 이동
            } while (t[current] != i);
            a[current] = temp;
            t[current] = current; //중요.
        }
    }
}

t[current] = current;를 통해 위치가 바뀐것을 반영해주지 않으면 재배치 완료한 cycle도 다시 돌 수 있다.
listSort에서처럼 link는 대충 보조수단 정도로만 보면 안되고, t도 보조는 맞지만 값 바뀐거 따라서 수정해줘야 제대로 돌아간다.(t값이 i랑 일치하는지 보고 정렬 수행하기때문에)

Analysis (tableSort)
$O(mn)$ (자세한건 p.369)

listSort2는 $3(n-1)$ records moves가 일어나는데반해, tableSort는 $⌊3n/2⌋$이므로 m이 크다면 table을 만들어 하는 편이 낫다.

---

7.9 SUMMARY OF INTERNAL SORTING

Insertion Sort는 list가 이미 부분적으로 정렬됐으때 사용하면 좋다.
규모가 작은 경우 best이다.

Merge Sort는 worst case기준 best였지만, heap sort보다 더 많은 공간을 필요로 했다.

Quick Sort는 average case기준 best였지만, worst case일때 O(n^2)이었다.

Radix Sort는 key의 size와 r(radix)에 영향을 받았다.

Method	Worst	Average
Insertion sort	$n^2$ (or $kn$)	$n^2$
Heap sort	$n\log n$	$n\log n$
Merge sort	$n\log n$	$n\log n$
Quick sort	$n^2$	$n\log n$

quick sort와 insertion sort의 break even point를 $nBreak$라고 하자.
$n>nBreak$라면, qucik sort를 우선적으로 진행하고,
pivot 기준으로 크기를 나누다가 $nBreak$보다 작아진다면 insertion sort를 진행함으로써 performance를 향상시킬 수 있다.

worst case일때 merge sort가 대부분 best이다.
merge sort 또한 위와 비슷한 방법으로 insertion sort와 연계해 performance를 증가시킬 수 있다.

asymtotic complexity analysis가 그렇게 정확하진 않다.
n이 작을때 특히 그렇고, 같은 식으로 표현돼도 실제 실행 시간은 다를 수 있다.

내 머릿속에 있는대로 한번 더 정리하자면 일단 제일 처음 배운 (1)insertion sort는 O(n^2) (or O(kn),
그래서 더 빠른 (2)quick sort는 평균이 O(nlog n)이긴하나 worst가 O(n^2)이었다.
(O(nlog n) 중에 가장 빠르도가는 함)
그래서 worst도 O(nlog n)인 (3)merge sort를 배우고, merge 보다 공간은 덜 필요하지만 같은 시간복잡도인 (4)heap sort를 배웠다.
(heap이 merge보다는 좀 더 느리다고 한다.)

---

7.10 EXTERNAL SORTING

7.10.1 Introduction

정렬해야할 자료가 너무 커서 internal memory에 넣지 못하는 경우(== internal sort impossible)

block 은 disk로부터 한번에 읽거나 쓰는 data이다.
block을 읽거나 쓰는데 걸리는 시간에 영향을 주는 요소는 (1)Seek time, (2)Latency time, (3) Transmission time이 있다.(뭔지는 p.376)

가장 유명한 방법: merge sort
input list로부터 segment를 받아와서 internal sorting 기법으로 정렬 후, 다시 external storage에 저장(이런 sorted segment를 run이라고 함)
runs를 가져와 merge sort 진행
run이 1개 남을때까지 반복

Example

4500 records를 정렬해보자.
block size는 250이고, internal memory size는 750이다.

우선 750 records씩 6개의 정렬된 runs를 external storage에 작성
750의 internal memory를 3구역으로 나눔, 2개는 input buffer, 1개는 ouput buffer
이를 이용해 run 2개씩 merge sort 진행한다.
각 run을 3등분해서 input buffer에 각각 넣는다. output buffer에 적다가 꽉차면 external storage에 flush하는 방식으로 진행한다.
그렇게 run1-run2, run3-run4, run5-run6을 merge sort하고, 모든 runs이 하나로 합쳐질때까지 쭉 진행한다.

.
.
.

분석해보면, data에 일어나는 pass 수가 time에 많은 영향을 미친다.

그리고, CPU processing과 I/O가 병렬로 처리된다면 시간이 꽤 단축될 수 있다.
nonmultiprogramming environment에선 이런 병렬처리가 중요하지만, multiprogramming environment에선 OS구조상 불가능 할 수 있어서 크게 중요하진 않다.

전자의 경우 higher-order merge로 merge passes 수를 줄이고(7.10.2),
후자의 경우 적절한 buffer-handling scheme으로 parallel I/O, merging을 하도록 한다(7.10.3).
추가로 loser-tree strategy로 runs 수를 줄여 시간을 단축 할 수도 있다(7.10.4).

...
요약하자면(서론수준으로),
merge pass 수 줄여서 I/O 수를 줄이려고하는 경우 higher-order merge 방식을 사용하는데(not two-way merge), CPU 연산 수를 줄이려고 loser tree를 사용한다.
k개의 runs에대해 최소 buffer size는 k+1(input: k, output: 1)이지만 병렬 수행을 위해 어떤 값이 최선인지 찾는다.
그리고 병렬 수행이 가능한 긴 runs을 찾는(만드는) loser tree를 이용한 algorithm도 알아본다.
(만든 runs의 길이가 다를 경우 merging을 최적화 하는 방법이 7.10.5에 나오며 마무리)

이정도까지만 보고 필요하면 자세히 다시 공부하기