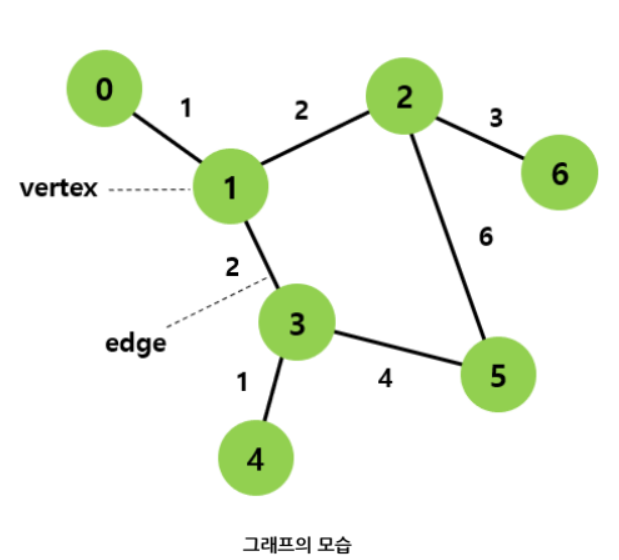
개요

• 회사의 조직도와 같은 계층을 표현하거나 인스타그램 친구 관계도를 표현하는 것처럼 선형 자료구조로는 표현할 수 없는 문제가 있다.
• 위와 같은 비선형적 문제를 다룰 수 있는 자료구조가 그래프이다.
• 그래프는 관계에 특화된 자료구조로 정점(Vertex)과 간선(Edge)으로 구성되어 있다.

1. 정점은 Vertex라고도 하고 Node라고도 함

• 각 정점은 고유하게 식별되는 객체이고, 간선은 정점 간의 관계를 표현한다.
  

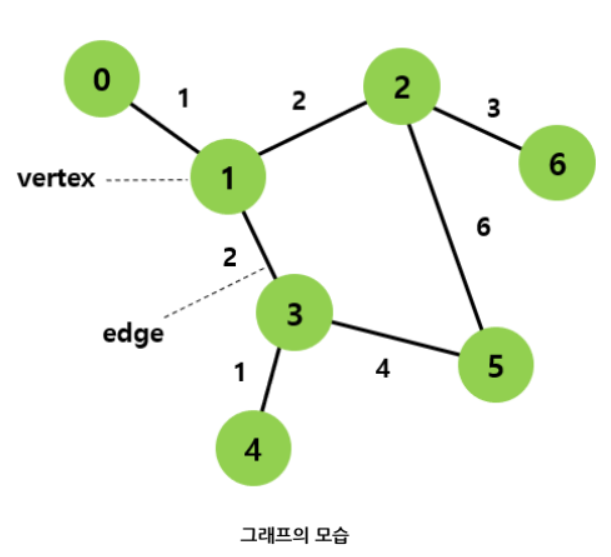
종류

• 그래프의 종류에는 간선이 방향성을 가지는 지에 따라 방향 그래프와 무방향 그래프로 구분할 수 있다.
• 간선이 단순 연결 이상의 정보(가중치)를 가지는 가중치 그래프도 있다.

1. 네트워크(Network)라고도 함
   

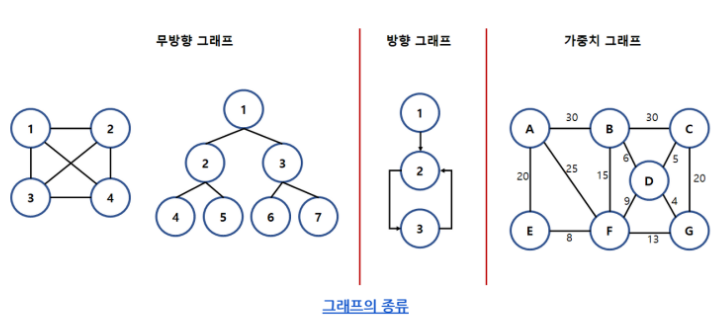
용어

• 간선으로 연결된 정점끼리는 인접하다고 하며, 해당 간선은 연결된 정점에 부속되어 있다고 한다.
• 정점에 부속되어 있는 간선의 수를 차수라고 하며 정점으로 들어오는 방향이면 진입 차수, 나가는 방향이면 진출 차수라고 한다.
• 한 정점에서 다른 정점까지 간선으로 연결된 정점을 순서대로 나열한 리스트를 경로(Path)라고 한다.
• 경로를 구성하는 간선 수를 경로 길이(Path Length)라고 하며, 모두 다른 정점으로 구성된 경로를 단순 경로라고 한다.
• 단순 경로 중 경로의 시작 정점과 마지막 정점이 같은 경로를 사이클(Cycle)이라고 한다.
• 경로가 있으면 정점끼리 연결 되었다고 한다.

1. 모든 정점이 연결되어 있다면 연결 그래프, 아니면 단절 그래프

표현

• 그래프를 표현하는 방법에는 인접 행렬과 인접 리스트가 있다.
• 인접 행렬과 인접 그래프 둘 다 인접한 정점 사이를 잇는 간선의 정보를 저장한다.

인접 행렬

• 인접 행렬은 정점이 N개 있을 경우 N * N 크기의 2차원 배열로 그래프를 표현한 것이며, 배열의 원소는 간선의 가중치를 저장한다.
• 연결되어 있지 않은 경우 0 혹은 무한대 값으로 표현한다.
• 연결되지 않은 정보도 저장하고 있기 때문에 그래프에 간선이 적다면 그만큼 메모리를 낭비하게 된다.

1. 이를 희소 그래프라고 하고, 반대는 밀집 그래프
   

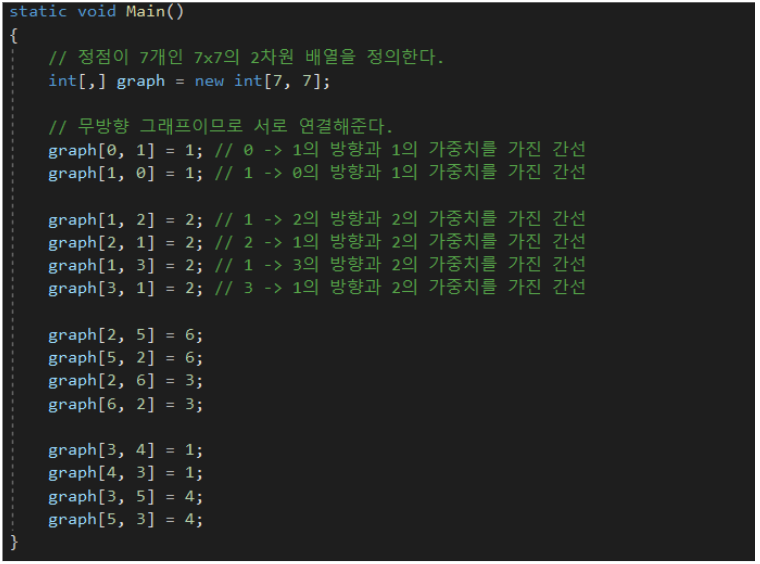
인접 리스트

• 인접 리스트는 연결된 간선만을 저장한다.
  
  

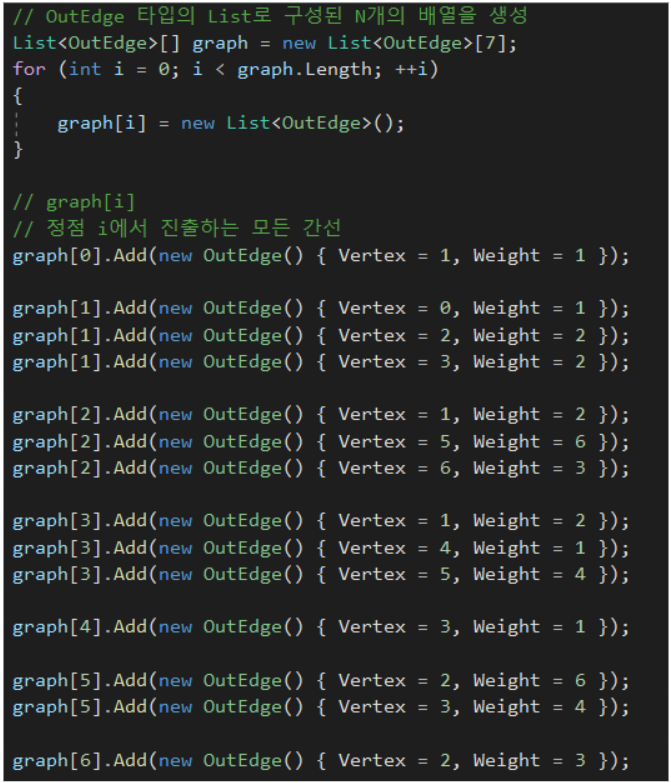
• 0번 정점(Vertex)은 1번 정점과 연결되어 있고 가중치는 1이다.
• 1번 정점은 0, 2, 3번 정점들과 연결되어 있고 가중치는 각각 1, 2, 2이다.
• 2번 정점은 1, 5, 6번 정점들과 연결되어 있고 가중치는 각각 2, 6, 3이다.
• 3번 정점은 1, 4, 5번 정점들과 연결되어 있고 가중치는 각각 2, 1, 4이다.
• 4번 정점은 3번 정점과 연결되어 있고 가중치는 1이다.
• 5번 정점은 2, 3번 정점들과 연결되어 있고 가중치는 각각 6, 4이다.
• 6번 정점은 2번 정점과 연결되어 있고 가중치는 3이다.
• 위의 인접 행렬과 인접 리스트 예시는 아래 그림을 나타낸다.