가설 검정
-
가설 검정 = 가설(Hypothesis) + 검정(Testing)
-
가설(Hypothesis) : 주어진 사실 또는 조사하려고 하는 사실에 대한 주장 또는 추측을 가설이라고 함.
-
통계학에서는 특히 모수를 추정 할 때 모수가 어떠하다는 증명하고 싶은 추측이나 주장을 가설이라고 함.
-
귀무 가설(Null hypothesis, Hο)
- 기존의 사실(아무것도 없다, 의미가 없다.)
- 대립가설과 반대되는 가설로 연구하고자 하는 가설의 반대의 가설로 귀무가설은 연구목적이 아님
- Ex) Hο : 코로나 백신이 효과가 없다, Hο:μ = 0
-
대립 가설(Alternative hypothesis : H₁)
- 데이터로 부터 나온 주장하고 싶은 가설 또는 연구의 목적으로 귀무가설의 반대
- Ex) H₁ : 코로나 백신이 효과가 있다, Hο:μ ≠ 0 or μ ≥ 0
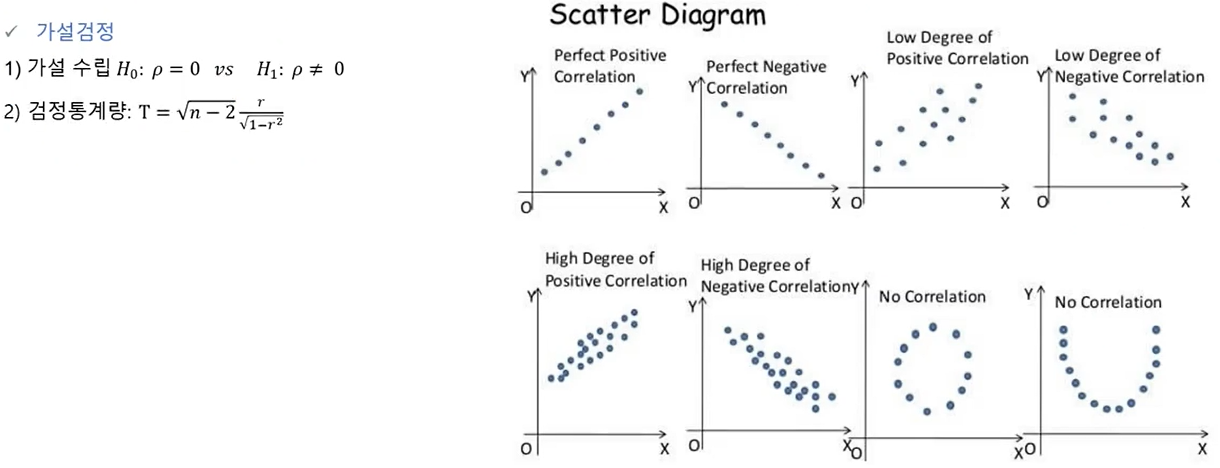
가설검정과 유의수준
-
제 1종 오류(type I error) : 귀무가설이 참이지만, 귀무가설을 기각하는 오류
- Hο를 기각할 확룰이 a라고 하면 채택하게 될 확률은 1 - a로 표시할 수 있음.
- 제1종 오류를 범할 확률의 최대허용 한계를 유의수준이라고 하며, a라고 표시
-
제 2종 오류(type II error) : 귀무가설이 기각해야 하지만, 귀무가설을 채택하는 오류
-
검정통계량 : 귀무가설이 참이라는 가정하에 얻은 통계량
-
검정결과 대립가설을 선택하게 되면 귀무가설을 기각(reject)함
-
검정결과 귀무가설을 선택하게 되면 귀무가설을 기각하지 못한다고 표현함.
-
P-value : 귀무가설이 참일 확률
- 0 ~ 1사이의 표준화된 지표(확들값)
- 귀무가설이 참이라는 가정하에 통계략이 귀무가설을 얼마나 지지하는지를 나타낼 확률
-
기각역(귀무가설을 기각시키는 검텅통계량의 관측값의 영역
-
가설 검정의 절차
- 가설 수립 : Hο : 코로나 백신이 효과가 없다, H₁ : 코로나 백신이 효과가 있다.
- 유의 수준 결정 : 유의 수준 a 정의
- 기각역 설정
- 감정통계량 계산
- 의사결정
-
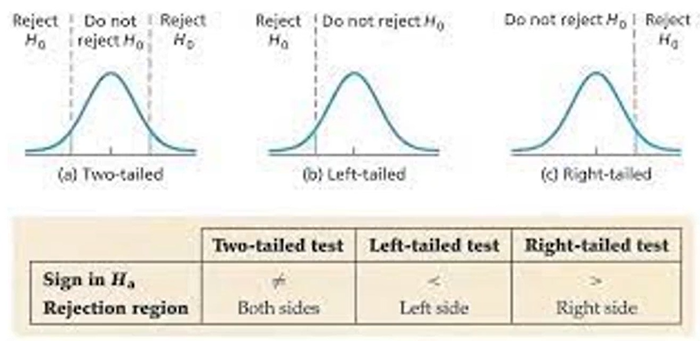
양측 검정(two-side test) : 대립가설의 내용이 같지 않다 또는 차이가 있다 등의 양쪽 방향의 주장
- A백신과 B백신의 코로나 면역력에는 차이가 있다.
- A팀과 B팀 연봉은 차이가있덲지.
-
단축 검정 : (one-side test)
-
A제품의 수율이 제품의 수욜이 B제품의 수율보다 크다
-
A팀의 평균 연봉이 B팀의 평균 연봉보다 크다
단일 표본에 대한 가설검증
-
모평균 가설검정 - 모분산을 아는 경우

-
모평균 가설검정 - 모분산을 아는 경우 (예시)

- 모평균 가설검정 - 모분산을 모르는 경우 (소표본)

- 모비율 가설검정

두개의 표본에 대한 가설검정
- 대표본 - 모분산을 아는 경우

- 예시

-
소표본 - 모분산을 모르는 경우(엑셀 : t검점 등분산 비교)

- 대표본 = ~Z
- 소분포(σ²을 알때) = ~Z
- 소분포(σ²을 모를때) = ~t(t분포)
- 대응 비교(엑셀 : 쌍체비교)

범주형 자료분석
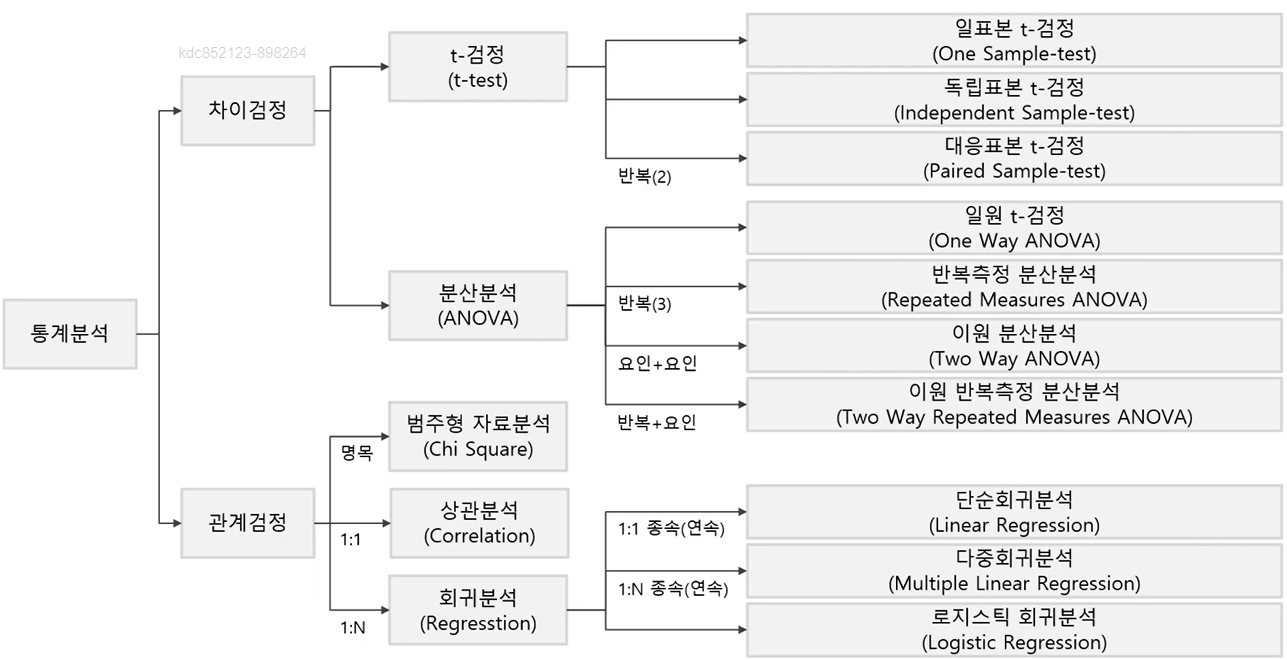
적합도 검정
-
범주형 자료(categorical data) : 관측된 결과를 어떤 속성에 따라 몇 개릐 범주로 분류 시켜 도수로 주어진 데이터
-
범주형 자료 분석(categorical data analysis)
- 범주형 자료에 대한 통계적 추론 방법
- 범주형 자료 분석은 카이제곱 검정으로 추론함
-
t-test와 카이제곱 검정의 차이
- t-test : 연속형 변수의 차이에 대한 검정
- 카이제곱 검정 : 명목형 변수에 대한 검정
-
적합도 검정(goodness of fit test)
- 관측된 값들이 추론하는 분포를 따르고 있는지 검정, 한 개의 요인을 대상으로 검정
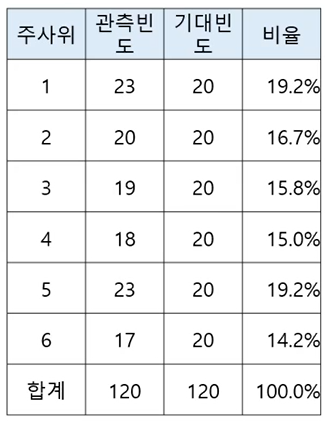
ex) 멘델의 유전 법칙에 부합하는지 검사하기 위해 테스트할 때, 완두콩의 잡종 비율이 A:B:C = 1:1:2 였다고 가정해 보자.
100개의 콩을 조사한 결과 A가 25 B가 20 C가 55개 였다면 앞선 가정이 맞는지 유의수준 0.05에서 검정해보자.
- 관측된 값들이 추론하는 분포를 따르고 있는지 검정, 한 개의 요인을 대상으로 검정
- 독립성 검정(test of independence)
- 관측된 값을 두 개의 요인으로 분할하고 각 요인이 다른 요인에 영향을 끼치는지(독립)를 검정
- 지지하는 정당과 사는 지역(A,B,C구)은 관련이 있는지 알아보기 위해서 1000명을 뽑아서 조사한 자료가 있을 때, 지지 정당과 사는 지역이 독립인지 유의수준 0.05에서 검정해보자.
- 동질성 검정(test of homogeneity)
- 서로 다른 세개 이상의 모집단으로 관측된 값을이 범주내에서 동일한 비율을 나타내는지 검정
예시) 남녀의 핸드폰 선호가 동일한지 조사하기 위해서 남자 100명, 여자 200명을 조사하였다. 유의수준 0.05에서 동일한지 조사하여라.
- 서로 다른 세개 이상의 모집단으로 관측된 값을이 범주내에서 동일한 비율을 나타내는지 검정


독립성 검정
- 독립성 검정(test of independence)
- 관측된 값을 두 개의 요인으로 분할하고 각 요인이 다른 요인에 영향을 끼치는지(독립)를 검정

- 관측된 값을 두 개의 요인으로 분할하고 각 요인이 다른 요인에 영향을 끼치는지(독립)를 검정
- 지지하는 정단과 사는 지역(A,B,C구)은 관련이 있는지 알아보기 위해서 1000명을 뽑아서 조사한 자료가 있을 때, 지지정당과 사는 지역이 독립인지 유의수준 0.05에서 검정해보자.
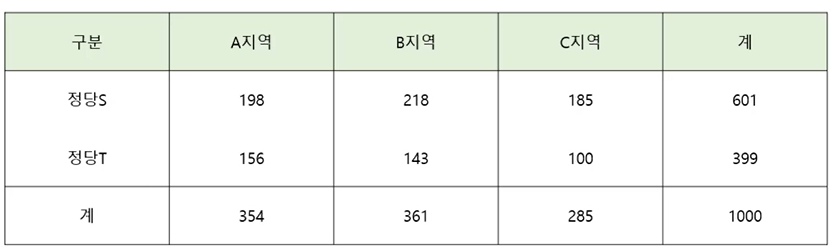
- 가설 : Hο : 지역과 지지하는 정당은 서로 독립이다 vs H₁ : 지역과 지지하는 정당은 서로 독립이 아니다.
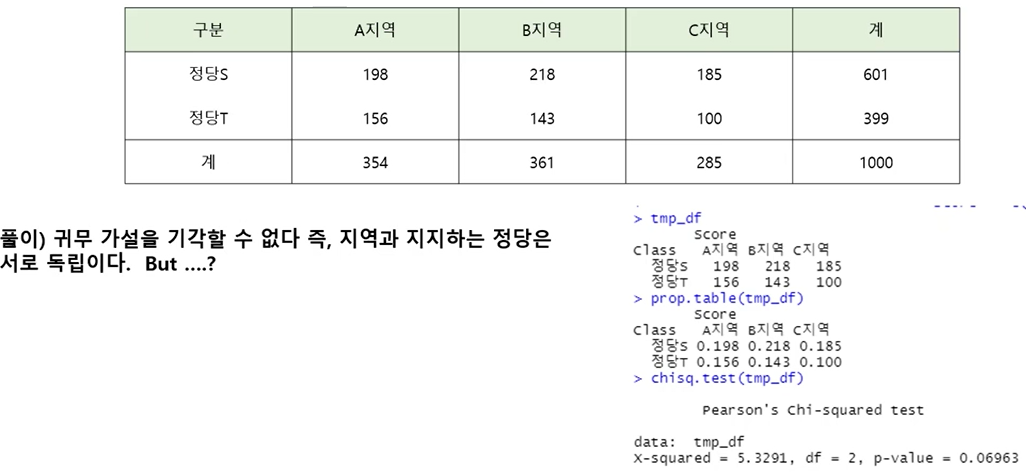
동질성 검정
- 동질성 검정(test of homogeneity)
- 서로 다른 모집단에서 관측된 값을이 범주내에서 동일한 비율을 나타내는지 검정
예시) 남녀의 핸드폰 선호가 동일한지 조사하기 위해서 남자 100명, 여자 200명을 조사하였다 유의수준 0.05에서 동일한지 조사하여라.
-가설 : Hο : 남녀간의 선호하는 핸드폰 회사는 동일하다. vs H₁남녀간의 선호하는 핸드폰 회사는 동일하지 않다.

- 서로 다른 모집단에서 관측된 값을이 범주내에서 동일한 비율을 나타내는지 검정
상관분석 & 회귀분석
상관관계
-
상관관계(correlation coefficient)
- 두 변수간의 함수 관계가 선형적인 관계가 있는지 파악할 수 있는 측도가 상관계수 임

- 두 변수간의 함수 관계가 선형적인 관계가 있는지 파악할 수 있는 측도가 상관계수 임
-
표본상관관계(sample correlation coefficient)
- 데이터가(x₁, y₁), (x₂, y₂), ···,(x¡,y¡)과 같이 i개의 쌍으로 주어 졌을때,
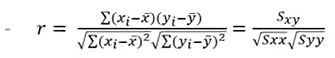
- 데이터가(x₁, y₁), (x₂, y₂), ···,(x¡,y¡)과 같이 i개의 쌍으로 주어 졌을때,
단순 회귀분석
-
회귀분석(regression analysis)
- 변수들간의 함수적 관계를 선형으로 추론하는 통계적 분석 방법으로 독립변수를 통해 종속변수를 예측하는 방법
- 비선형인 함수적 관계일 경우 비선형회귀(nonlinear regression)를 사용
ex) 마케팅 비용에 따른 매출액을 예측
-
종속변수(dependent variable)
- 다른 변수의 영향을 받는 변수로 반응변수라 표현 하기도 하며, 예측을 하고자 하는 변수
ex) 매출액, 수율, 불량율 등
- 다른 변수의 영향을 받는 변수로 반응변수라 표현 하기도 하며, 예측을 하고자 하는 변수
-
독립변수(independent variable)
- 종속변수에 영향을 주는 변수로 설명변수라 표현하기도 하며, 예측 하는 값을 설명해주는 변수
-
단순 회귀분석(simple regression analysis)
- 하나의 독립변수로 종속변수를 예측하는 회귀 모형을 만드는 방법을 단순 회귀분석이라고 함.
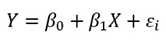
- 하나의 독립변수로 종속변수를 예측하는 회귀 모형을 만드는 방법을 단순 회귀분석이라고 함.
-
다중 회귀분석(multiple regression analysis)
- 2개 이상의 독립변수로 종속변수를 예측하는 회귀 모형을 만드는 방법을 다중 회귀분석이라고 함.
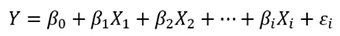
- 2개 이상의 독립변수로 종속변수를 예측하는 회귀 모형을 만드는 방법을 다중 회귀분석이라고 함.
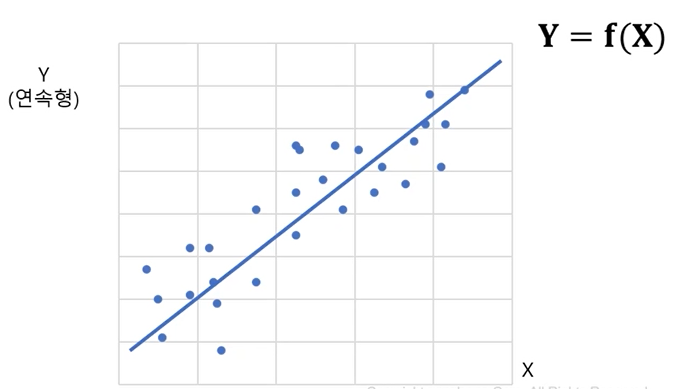
- 회귀모델링 분류
- X변수의 수, X변수와 Y변수의 선형성 여부에 따라 구분
- 독립변수가 1개일때 (단순), 2개 이상일 때 (다중)
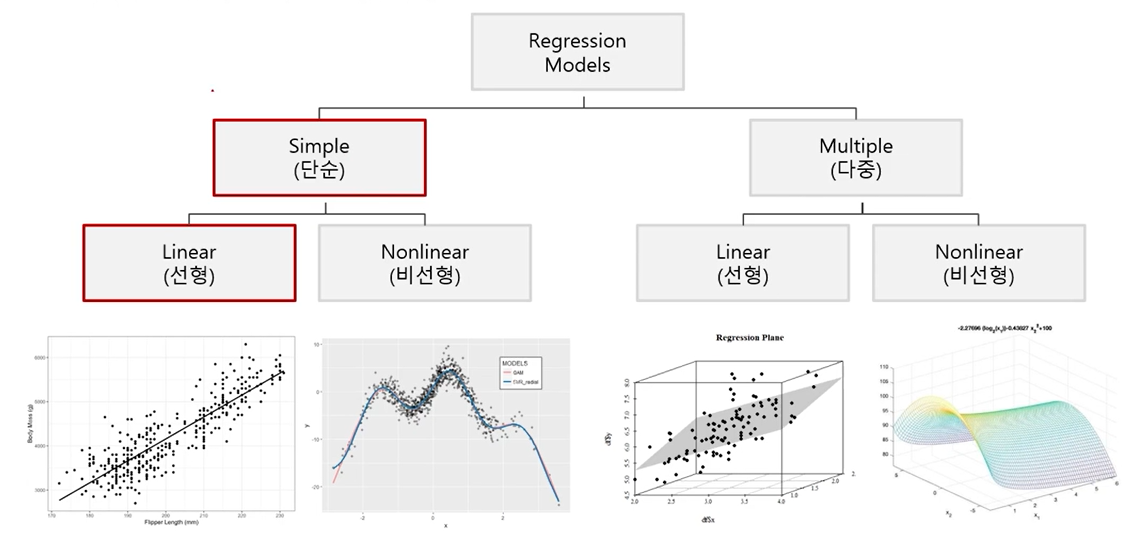
- X변수의 수, X변수와 Y변수의 선형성 여부에 따라 구분
- 단순 회귀분석 예시(1)
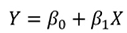
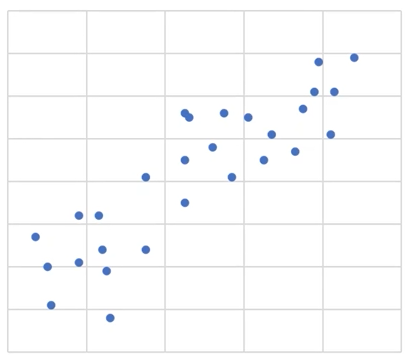
파라미터를 표현하여 점과 점의 기울기를 구할 수 있다. 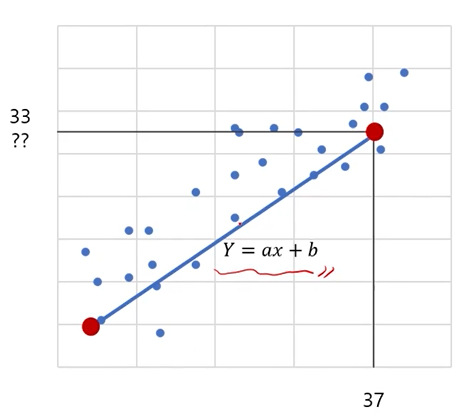
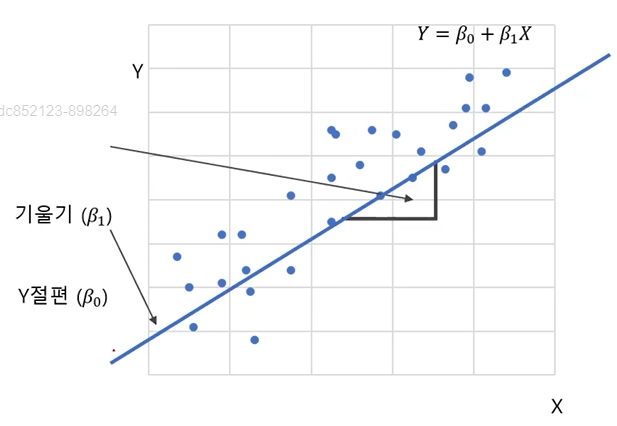
- 단순 회귀분석 예시(2)
- 회귀선으로부터 각 관측치으 ㅣ오차를 최소로하는 선을 찾는 것이 핵심
- 오차를 최소로 하여 β。,β₁을 추정하는 방법을 최소제곱법(method of least squares)이라 함 (β : 베타)
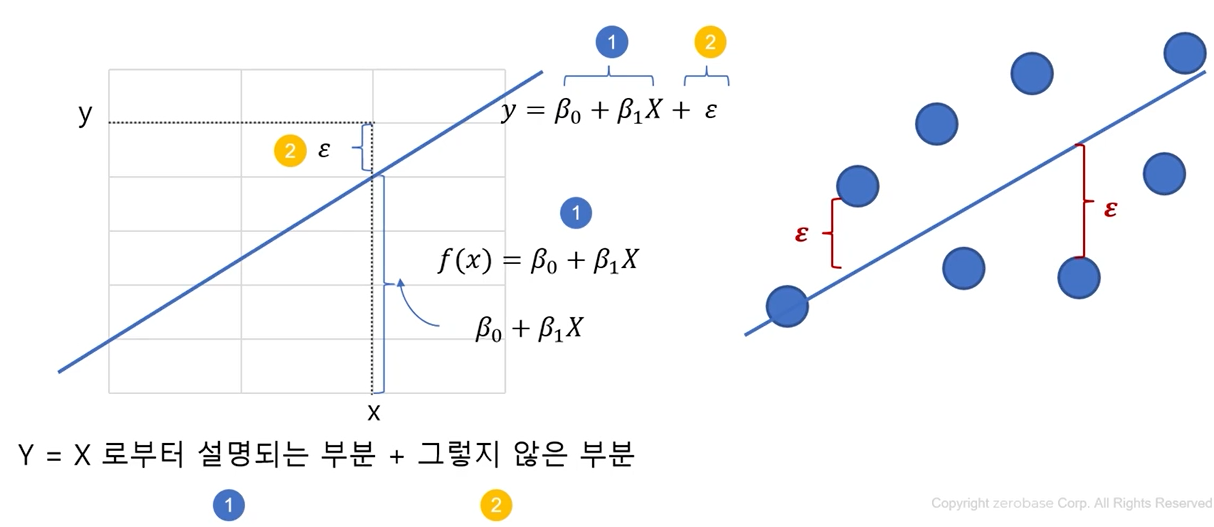
- 최소 제곱법
- 회귀 모형의 모수 β。,β₁을 추정하는 방법중 하나를 최소 제곱법이라고 하며, 회귀 모형의 모수를 회귀 계수라고 함.
- 최소 제곱법을 통해 구한 추정량을 최소제곱추정량(LSE)라고 하며, 최소제곱법을 통해 회귀모형의 모수를 추정하는 것을 OLS(Ordinary Least Square)라고 함
- 회귀모형의 오차에 대하여 기본 가정이 있음.

β。(베타0), β₁(베타1)을 유도하기 위해 아래와 같이 편미분을 사용
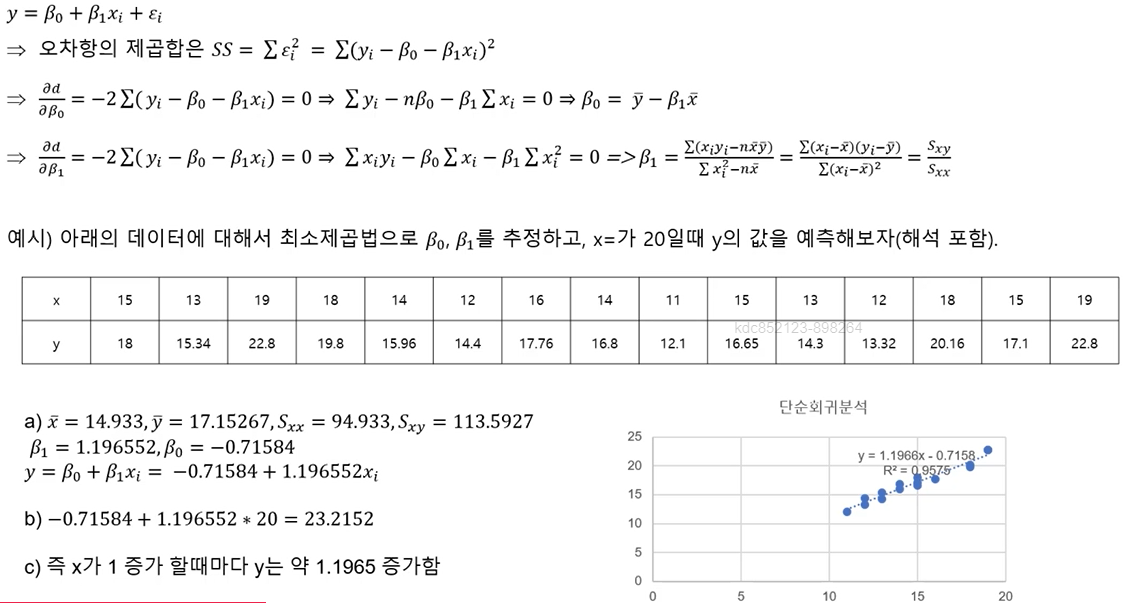
-
분산분석표
- 추정된 회귀식에 대한 유의성 여부는 분산분석을 통해서 회귀식의 유의성을 판단 할 수 있음
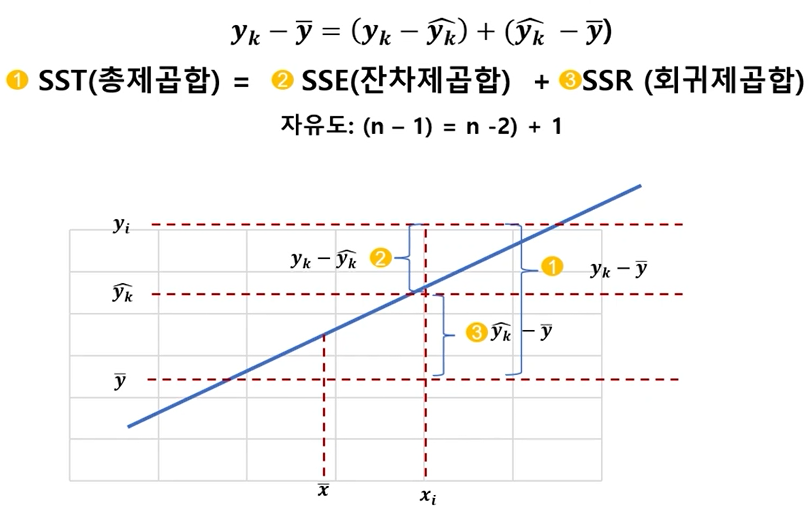
- 제곱합을 각각의 자유도 나눈 값을 편균제곱(mean square)라고 함

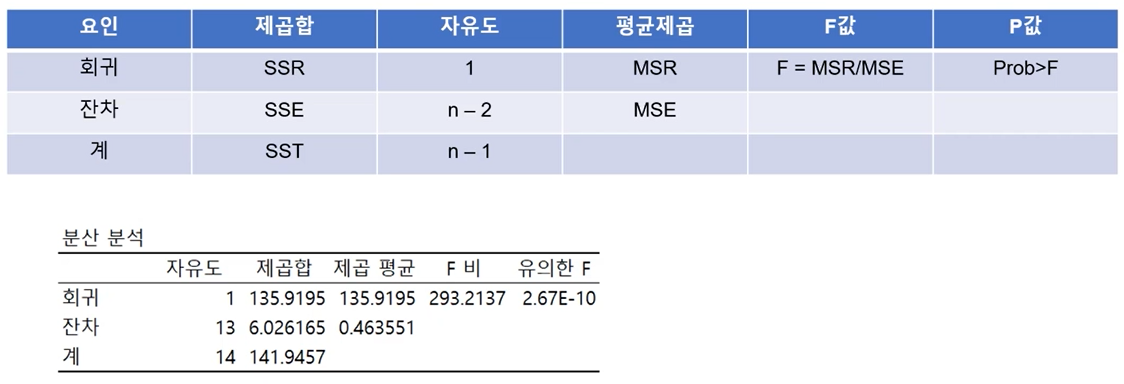
- 회귀분석의 추론과 가설 검정

- 결정계수(Coefficient of determination : R²)
- 추정된 회귀식이 얼마나 전체 데이터에 대해서 적합한지(설명력이 있는지)를 수치로 제공하는 값
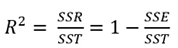
- 0과 1사이에 값으로 1에 가까울수록 추정된 모형이 설명력이 높다고 할 수 있음
- 0이라는 것은 추정된 모형이 설명력이 전혀 없다고 할 수 있음

- 추정된 회귀식이 얼마나 전체 데이터에 대해서 적합한지(설명력이 있는지)를 수치로 제공하는 값
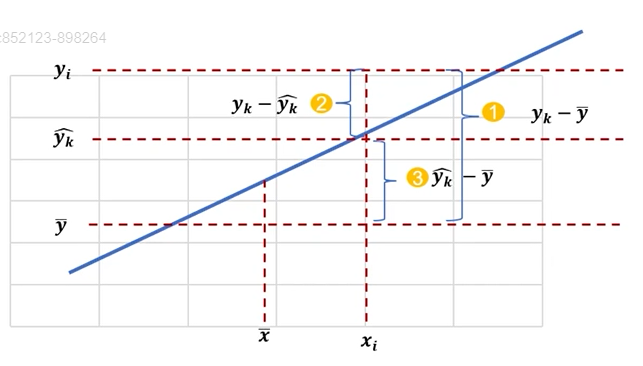
-
수정 결정계수(Adjust R²)
-
R²은 유의하지 않은 변수가 추가되어도 항상 증가됨(다중회귀)
-
Adjust R²은 특정 계수를 곱해 줌으로서 R²가 항상 증가하지 않도록 함.
-
보통 모형 간의 성능을 비교할 때 사용함
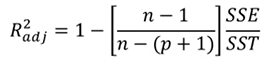 (p는 변수의 개수)
(p는 변수의 개수) -
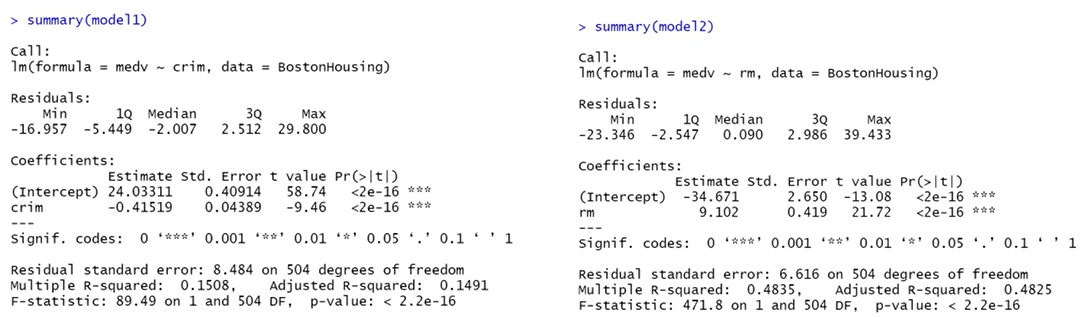
Boston Housing Price(보스턴 주택 가격 데이터)
-
medv : 주택가격 / crim : 자치시(town) 별 1인당 범죄율 / RM : 주택 1가구당 평균 방의 개수
-
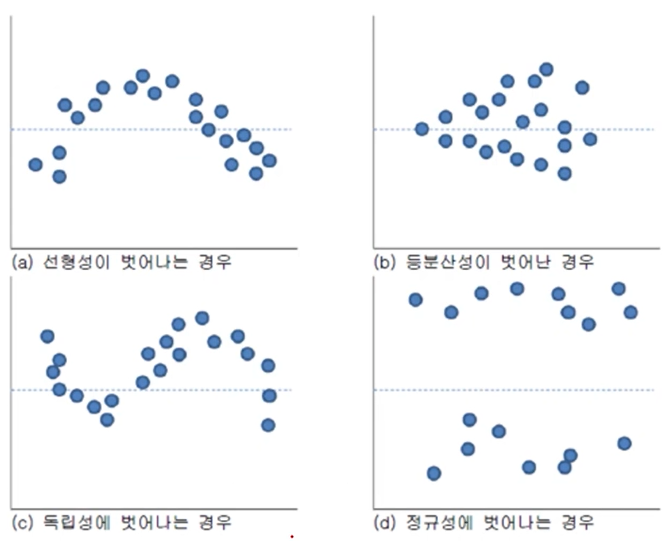
- 잔차분석
a) 선형성을 벗어나는 경우- 종속변수와 독립변수가 선형 관계가 아님
b) 등분산성이 벗어난 경우 - 일반적인 회귀모형 사용 불가능
- 등분산성 가정 위배
c) 독립성에 벗어나는 경우 - 시계열 데이터 또는 관측 순서에 영향을 받는 데이터에서는 독립성을 담보 할 수 없음(Durbin-Watson test 실행)
d) 정규성을 벗어나는 경우 - Normal Q-Q plot으로도 확인
- 잔차가 -2 ~ +2 사이에 분포 해야 함
- 벗어나는 자료가 많으면 독립성 가정 위배
- 종속변수와 독립변수가 선형 관계가 아님
분산분석
분산분석
-
분산분석(analysis of variance)
- 셋 이상의 모집단의 평균 차이를 검정
-
t-test : 두개의 모집단의 평균 차이를 검정
-
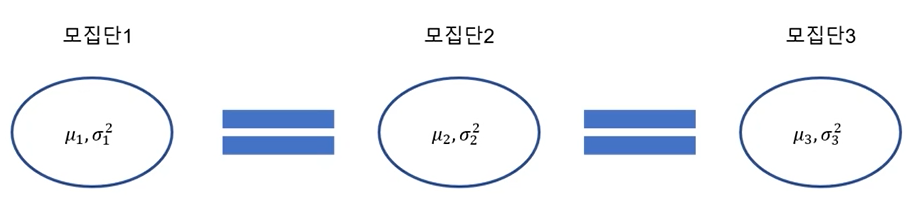
만약 아래의 평균 차이 검정을 t-test로 한다면
1) (모집단1 - 모집단2, 모집단1 - 모집단3, 모집단2 - 모집단3) 3번의 검증을 해야함
2) 오차가 커짐(α = 0.05인 경우 3번의 비교로 α = 1 - (1-0.05)³ = 0.143)
-
분산분석의 이해
-
실헙계획법(experimental design) : 모집단의 특성에 대하여 추론하기 위해 특별한 목적성을 가지고 데이터를 수집하기 위한 실험 설계를 실험계획법이라고 함
-
반응변수 : 관심의 대상이 되는 변수
-
요인/인자(Factor) : 실험 환경 또는 조건을 구분하는 변수를 실험에 영향을 주는 변수
-
인자수준 : 인자가 취하는 개별 값(처리 : treatment)
-
왜 분산분석일까?
- 모집단의 평균들을 비교하기 위하여 특성값의 분산 또는 변동을 분석하는 방법
- 실험을 통해 얻은 편차의 제곱합을 통해 평균의 차이를 검정
-
분산분석의 기본 가정
1) 각 모집단은 정규 분포를 따른다.
2) 각 모집단은 동인한 분산을 갖는다.
3) 각 표본은 독립적으로 추출되었다.

-
일원 분산분석 : 한가지 요인을 기준으로 집단간의 차이를 조사하는 것
-
이원 분산분석 : 두가지 요인을 기준으로 집단 간의 차이를 조사하는 것
-
다원 분산분석 : 세가지 이상의 요인을 기준으로 집단 간의 차이를 조사하는 것
-
예시
- 편의점 A~C(factor)

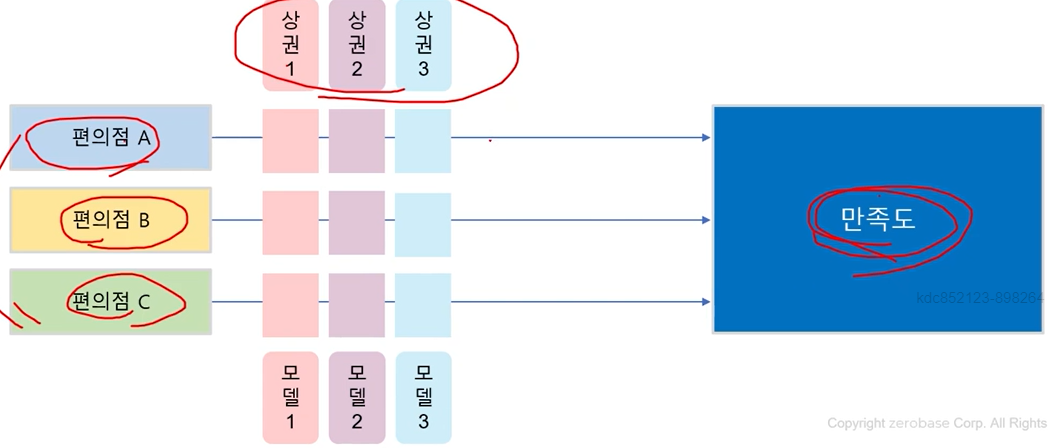
- 편의점 A~C(factor)
-
요인의 가짓수에 따라 분산분석이 달라진다.
One-Way ANOVA(일원배치법)
- One- Way ANOVA
- 한 개의 반응 변수와 한 개의 독립 인자
- 반응변수 : 연속형 변수만 가능
- 독립인자(변수) : 이산형 또는 범주형 변수만 가능





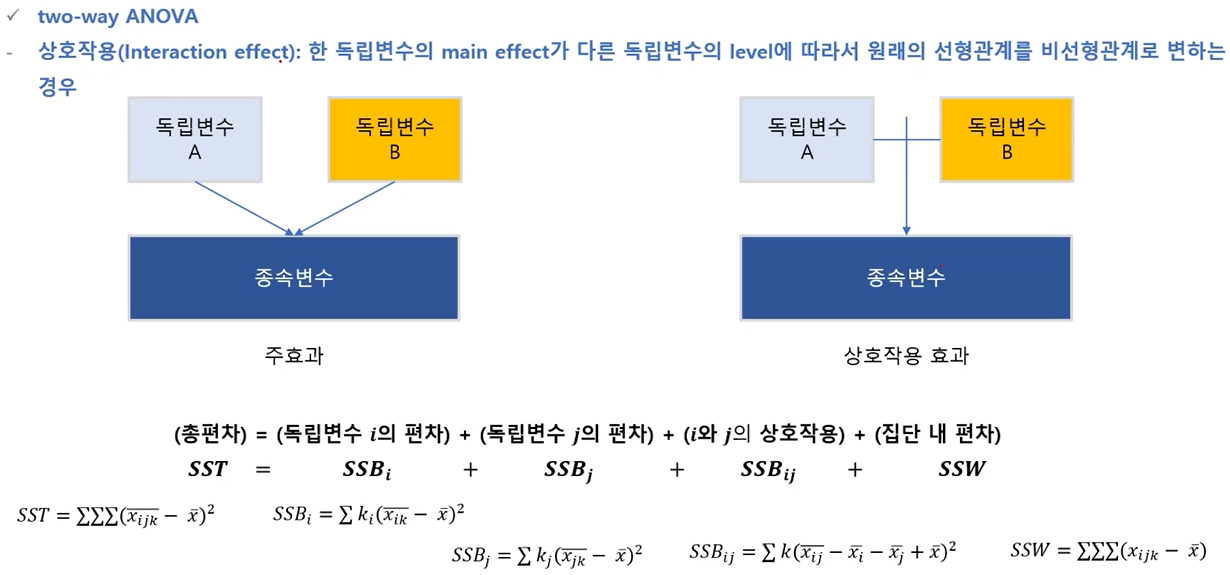
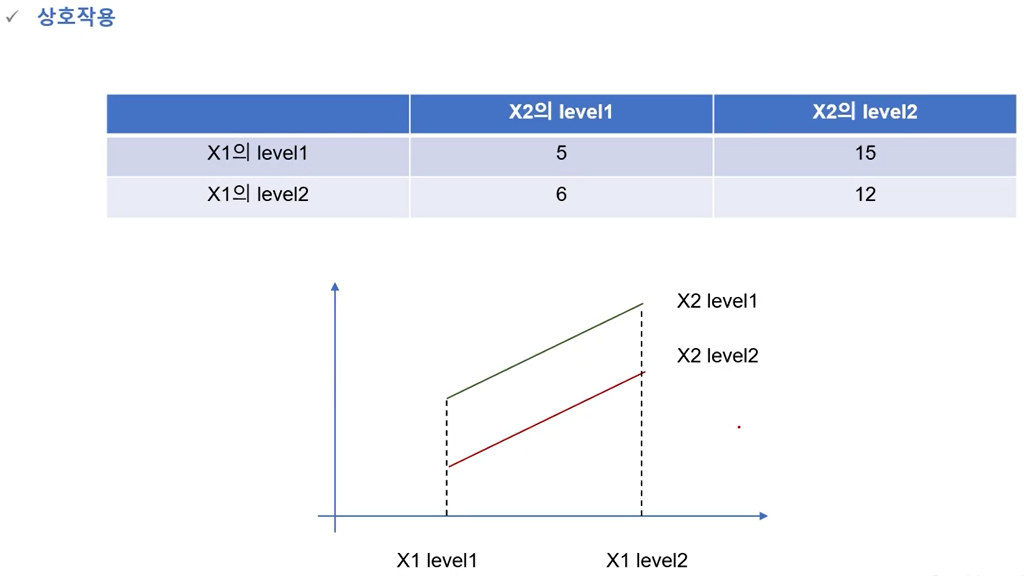
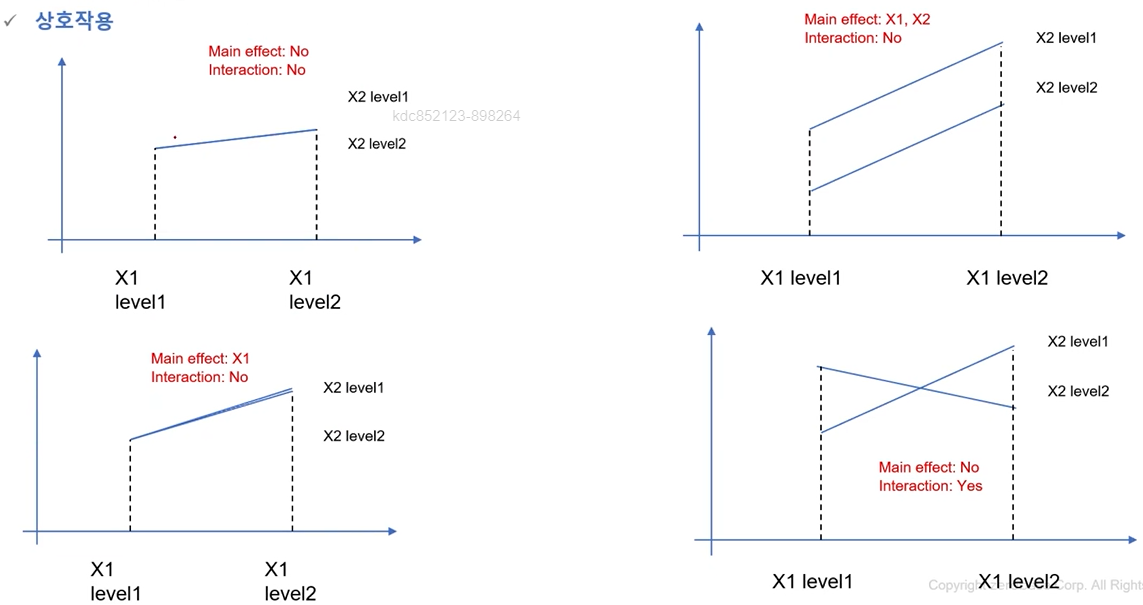
Two-Way ANOVA(이원배치법)
- two-way anova
- 한 개의 반응 변수와 두 개의 독립 인자로 분석하는 방법


시계열
시계열분석
- 시계열분석(time series analysis)
- 시계열(시간의 흐름에 따라 기록된 것) 자료(data)를 분석하고 여러 변수들간의 인과관계를 분석하는 방법
- 시계열데이터
- 시계열 데이터는 시간을 기준으로 관측된 데이터로, 보통 일->주->월->분기->년 또는 Hour등 시간의 경과에 따라서 관측한 데이터
- Ex) GDP, 주가, 거래액, 매출액, 승인금액 등을 시간의 흐름에 따라 정의한 데이터
- 시계열 데이터는 연속 시계열과 이산 시계열 데이터로 구분할 수 있음
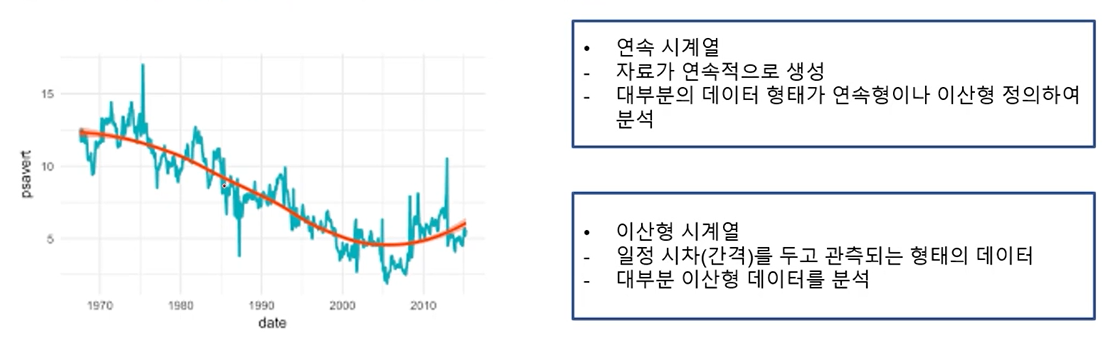
-
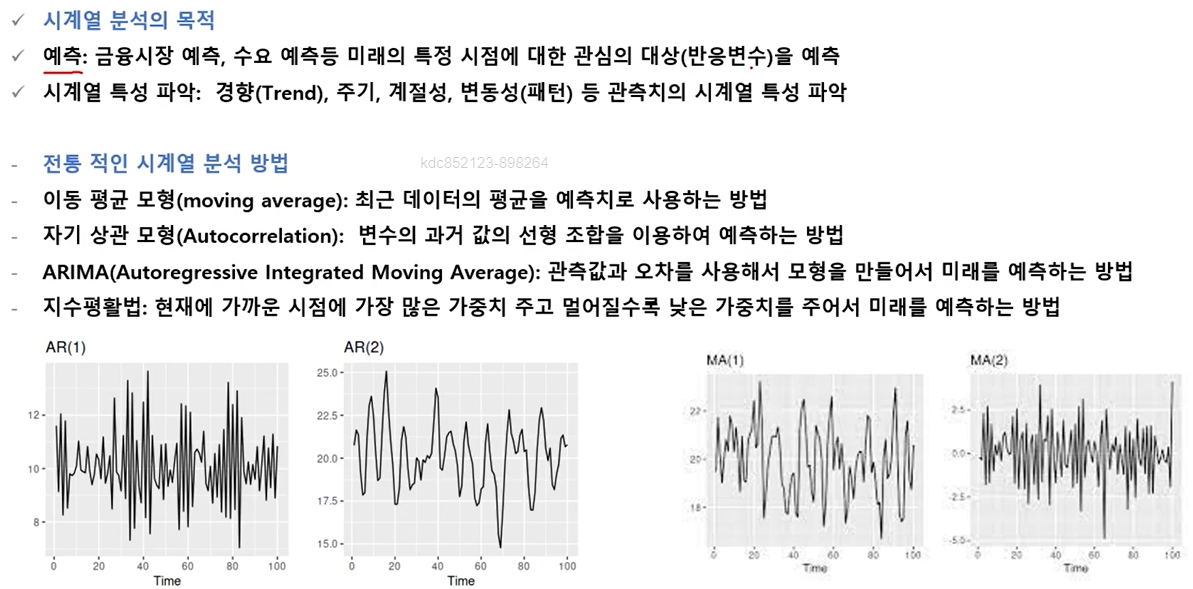
시계열 분석의 목적
-
시계열 요소
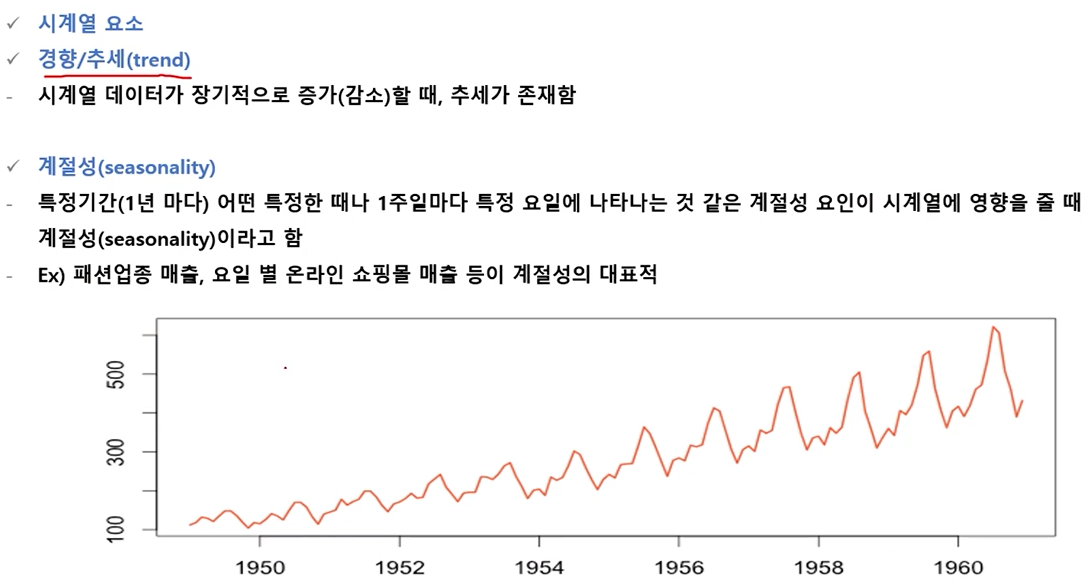
-
주기성
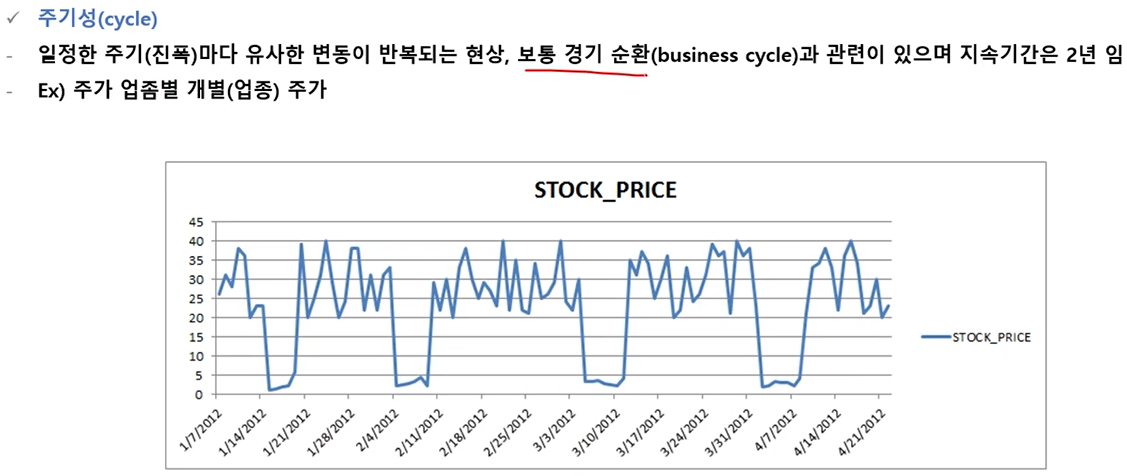
-
시계열 불규칙 요소
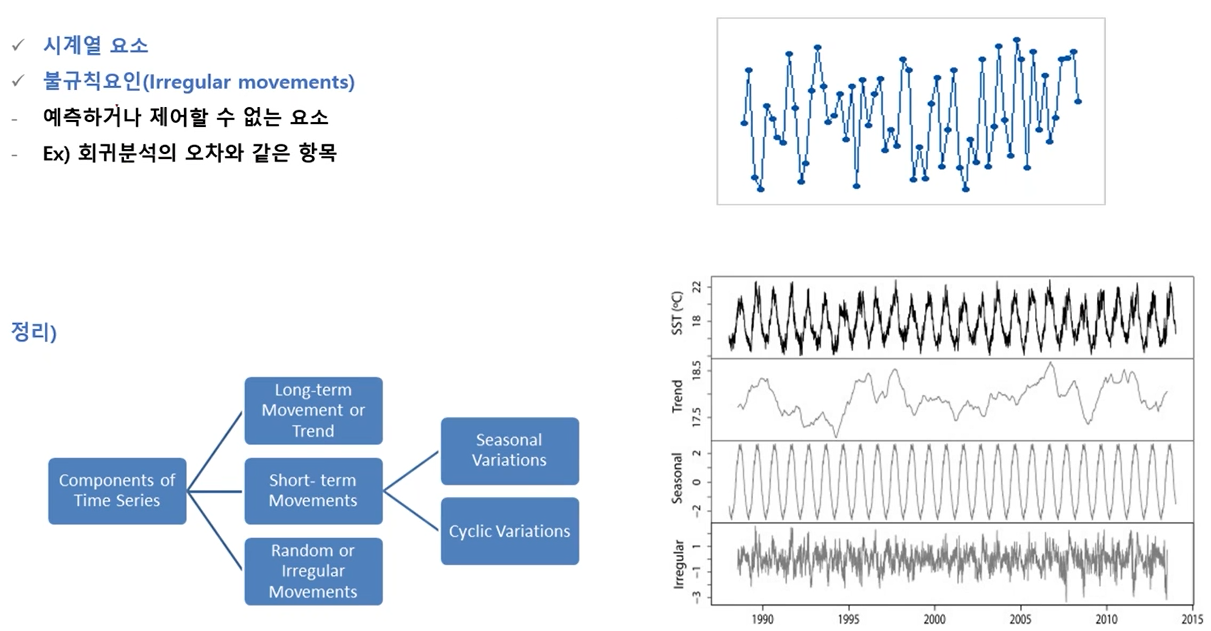
-
시계열 분석 방법

-
이동평균법
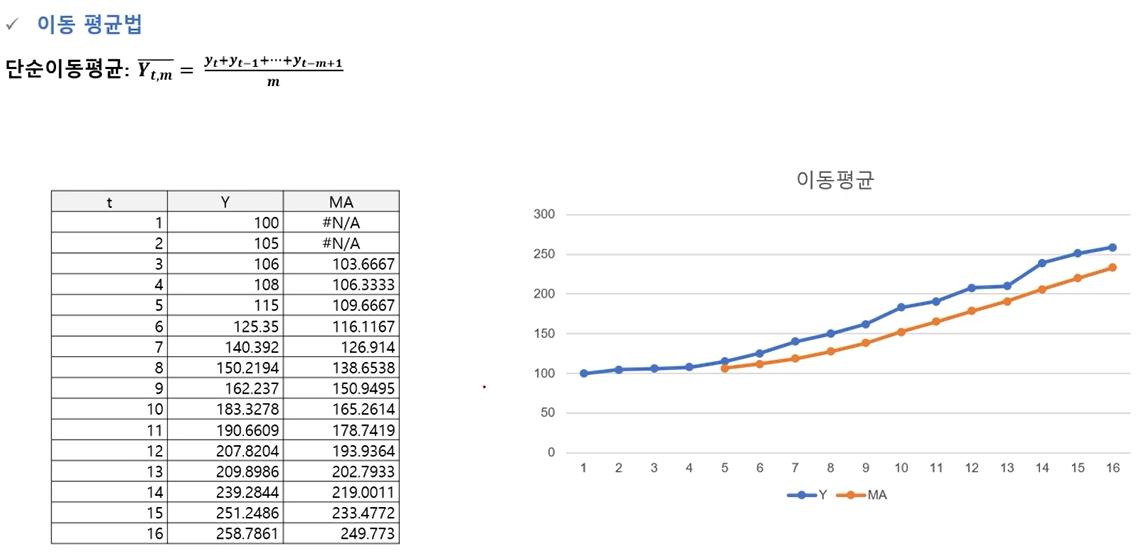
-
지수평활법
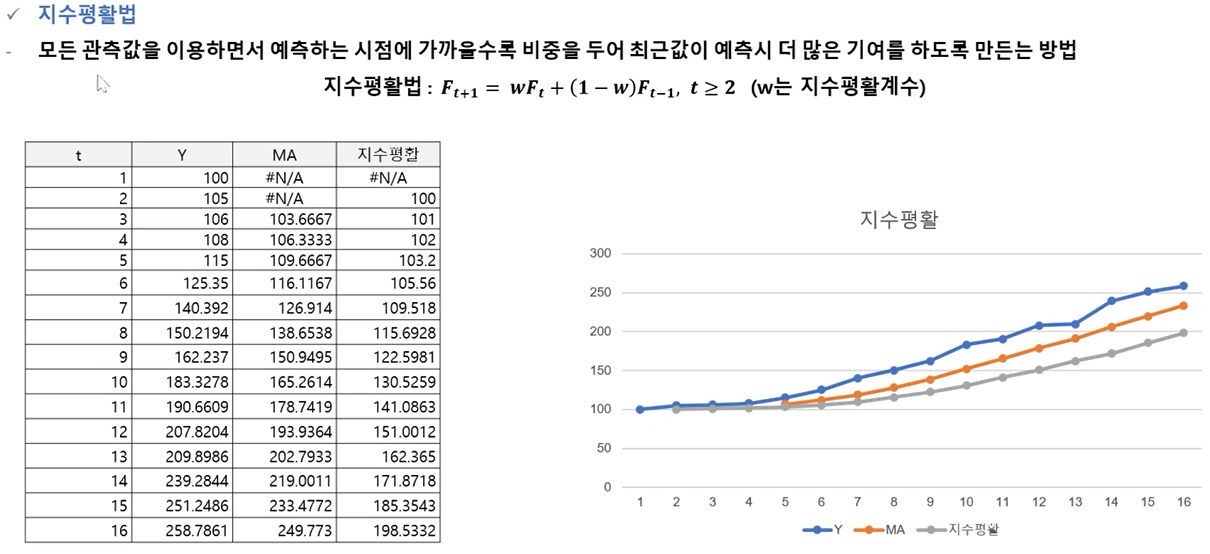
- 기초통계 활용하기