내적과 정사영

본 게시글에서는 내적과 정사영에 대해서 알아볼 것이다.

내적

• 내적은 두 벡터를 원소별로 곱한 후에 더한 scalar 값을 의미한다. 두 벡터 a와 b의 내적은 다음과 같다.
  

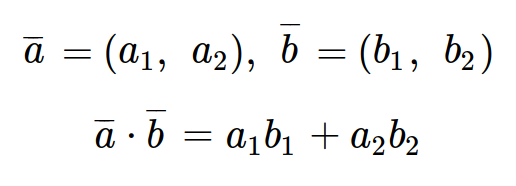
• 내적의 성질에 의해 다음과 같은 성질이 성립된다. 다음의 성질은 코사인 법칙을 이용하여 쉽게 증명되기 때문에, 직접 전개해봐도 좋을 것 같다.
  

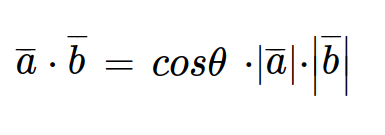
• 위의 식에서는 많이 쓰이는 cosine similarity (코사인 유사도)의 식도 찾아볼 수 있다.

• 벡터 a와 b의 norm을 고정해둔다면, cosine 값이 최대일 때, 즉 두 벡터의 방향이 일치할 때 내적 값이 최대가 되고, 두 벡터가 직교할 때 내적 값이 0이 된다.

정사영

• 내적의 기하학적 의미는 정사영과 관련이 깊다. 다음과 같은 두 벡터 a, b에 대해서 벡터 a를 벡터 b에 정사영해보자.

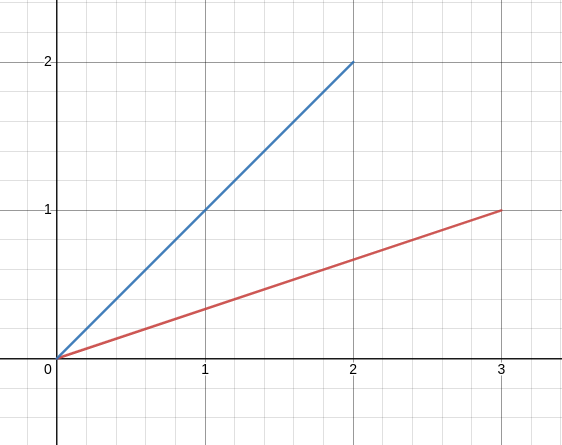
• 벡터 a는 (2, 2)이고, 벡터 b는 (3, 1)이다.

두 벡터 사이의 각도를 theta라고 한다면, 벡터 a를 벡터 b에 정사영한 결과의 norm은 다음과 같이 쉽게 구할 수 있을 것이다.

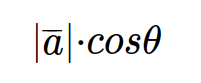
그리고 이것은 위에서 알아보았던 내적의 성질을 이용하여 다음과 같이 표현할 수 있다.

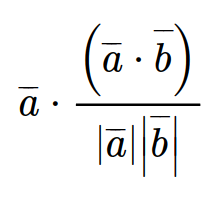
정사영의 의미를 생각해보면 벡터의 norm은 위와 같고, 벡터의 방향이 벡터 b와 같은 벡터를 찾으면 된다.
norm이 1이고, 벡터 b의 방향을 갖고 있는 벡터에 위의 norm을 곱해주면, 정사영 벡터를 얻을 수 있을 것이다.

여기에서 norm이 1인 벡터를 unit vector (단위 벡터)라고 한다.
norm이 1이고, 벡터 b의 방향을 갖고 있는 벡터는 다음과 같이 쉽게 구할 수 있다.

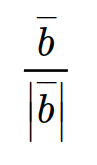
마지막으로 곱해주면 다음과 같이 정리할 수 있다.

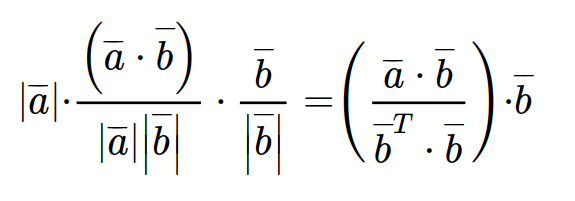
이렇게 본 글에서는 내적과 정사영에 대해서 알아보았다.