이전 글에서는 정책 그래디언트에 대해 알아보았으며, 본 글에서는 PG의 두 가지 한계점을 개선한 A2C에 대해 알아볼 것이다.
먼저 정책 그래디언트는 분산이 커서 학습이 불안정하며, 업데이트 주기가 길다는 한계점이 있었다.
정책 그래디언트를 다시 적어보자.
새로운 정책 그래디언트
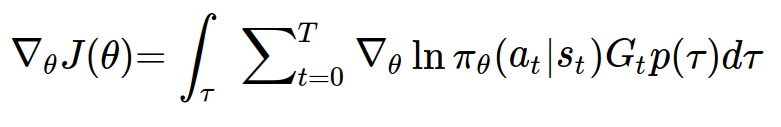
A2C에서는 Policy Gradient에서의 정책 그래디언트를 시간스텝 t를 기준으로 나누어 다음과 같이 새롭게 정의한다.
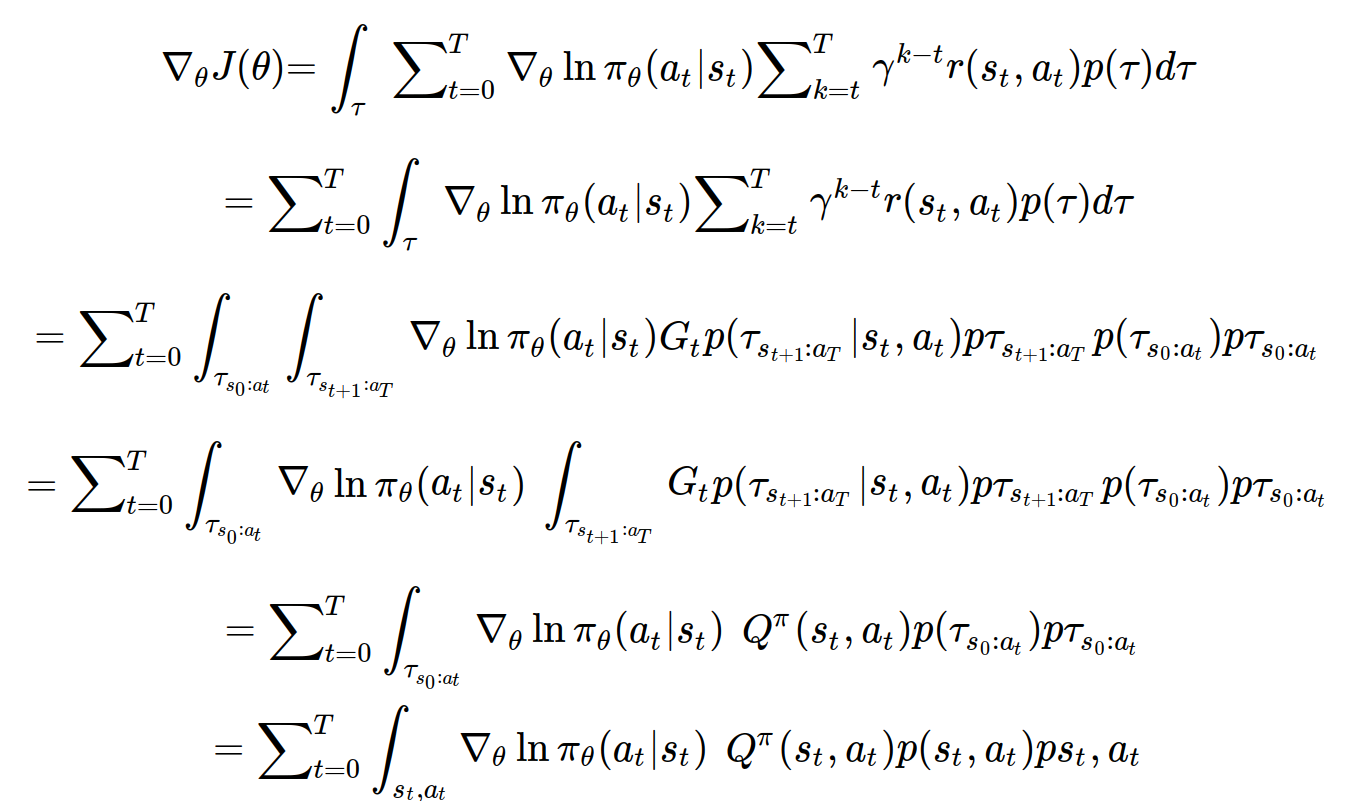
두번째 줄에서는 summation 기호를 적분기호 밖으로 빼주었다.
세번째 줄에서는 시간스텝 t를 기준으로 적분기호를 나누어주었다.
네번째 줄에서는 시간 t에 대한 함수인 로그 term을 적분기호 밖으로 빼주었고, t+1:T 궤도에 대한 적분기호 부분이 행동 가치 함수와 동일한 모습을 확인할 수 있다.
마지막 줄에서는 한계밀도함수와 같이 k<t인 궤도의 변수들은 모두 사라지게 되어, s_t와 a_t만 남게 된다.
위와 같이 정책 그래디언트를 행동 가치 함수로 표현함으로써 에피소드가 끝나야만 업데이트를 할 수 있었던 그 전과는 달리 이제는 행동가치함수를 잘 근사만 하면 매 시간스텝마다 업데이트를 할 수 있게 되었다. 행동가치함수를 근사하기 위하여 A2C에서는 행동가치함수를 parameterized 한다.
업데이트 주기가 길다는 한계점을 개선하였으니, 분산을 줄일 차례이다.
행동가치함수 자리에 시간스텝 t에 대한 상수인 b_t 를 넣어보자. b_t는 baseline이라고 한다.
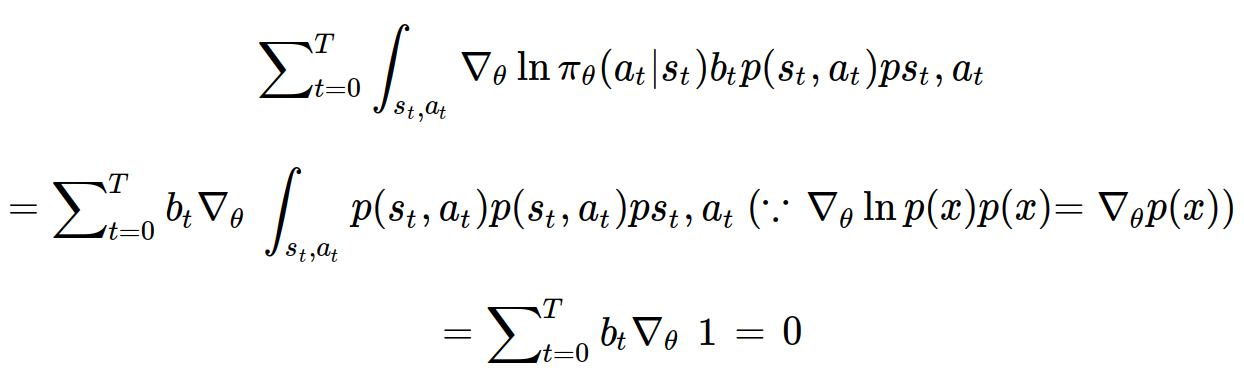
행동가치함수 자리에 상수를 대입하면 값이 0이 나오게 된다는 사실을 알 수 있다.
그렇게 우리는 다음과 같이 정책 그래디언트를 수정해줄 수 있고, baseline은 분산을 가장 줄일 수 있는 상수를 사용하는 것이 좋지만, 보통 상태가치함수를 사용하게 된다.
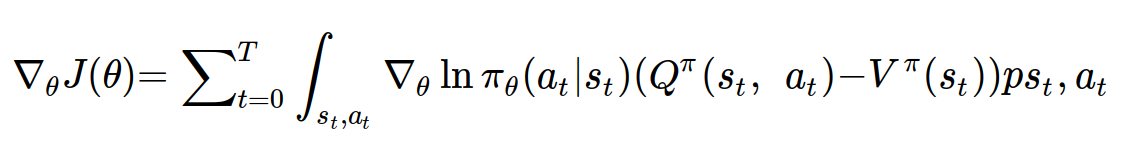
Q-V를 어드밴티지 함수라고 하며, Q값이 V(Q의 평균)와 비교하여 상대적으로 얼마나 더 좋은지 평가하는 measure가 될 수 있다.
A2C 알고리즘
REINFORCE 알고리즘과 마찬가지로 A2C 알고리즘 또한 미분식을 근사하여 구하여야 한다.
또한 정책(policy) 가중치와 어드밴티지(advantage, critic) 가중치, 총 2개의 모델 가중치를 학습시켜야 한다.
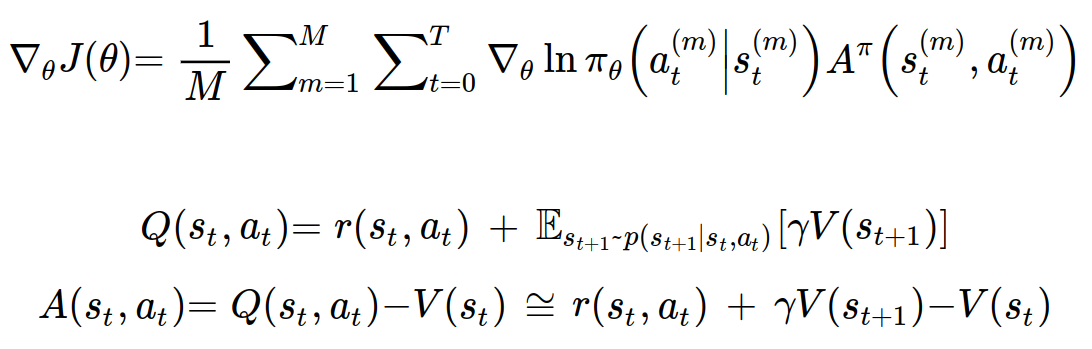
위와 같이 목적 함수를 근사하여 구할 수 있게 되었다.
또한 행동가치함수와 상태가치함수의 관계를 이용하여 어드밴티지 함수까지 상태가치함수의 표현식으로 근사하여 구할 수 있다.
이렇게 어드밴티지 함수를 구하는 문제는 상태 가치 함수를 구하는 문제로 바뀌게 되었다.
policy의 모델을 의미하는 actor와 상태 가치 함수 모델을 의미하는 critic 각각의 loss를 정의하면 다음과 같이 정의할 수 있다.
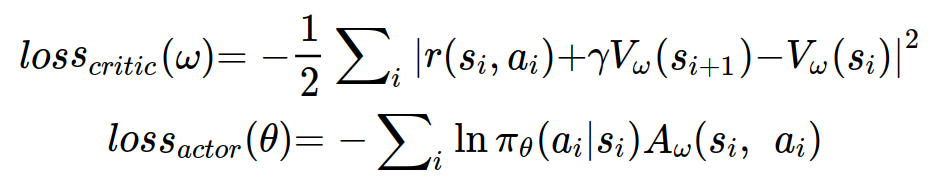
loss_actor의 A_w는 V_w로 근사적으로 구해지는 값으로 사용된다.
그리고 i는 batch data를 반복적으로 도는 것이다. batch size가 N이라면 N개의 s_i, a_i, s_i+1, r(s_i, a_i)에 대해서 값을 구하게 될 것이다.
batch_data는 N개의 연속된 데이터이다.
A2C는 정책 그래디언트보다 훨씬 좋은 성능을 보인다.
하지만 A2C도 한계점을 갖고 있다.
- on-policy 알고리즘이다.
- 하나의 batch 안에 있는 각각의 data들이 연속된 데이터이기 때문에, 강한 correlation을 갖고 있어 불안정적인 학습 결과를 초래할 수 있다.
다음 글에서는 강한 correlation 문제를 해결한 A3C에 대해서 알아볼 것이다.