최적의 policy를 찾기 위해서는 정의를 하는 것이 중요하다.
강화학습 문제의 근본
최적 policy는 보상의 기댓값을 최대로 만들어야 한다.
즉, 현재 보상만 고려하는 것이 아니라 미래의 보상들까지 고려하여 행동해야 한다.
보상의 기댓값을 반환값(expected return)이라고 하며, 다음과 같이 표현한다.
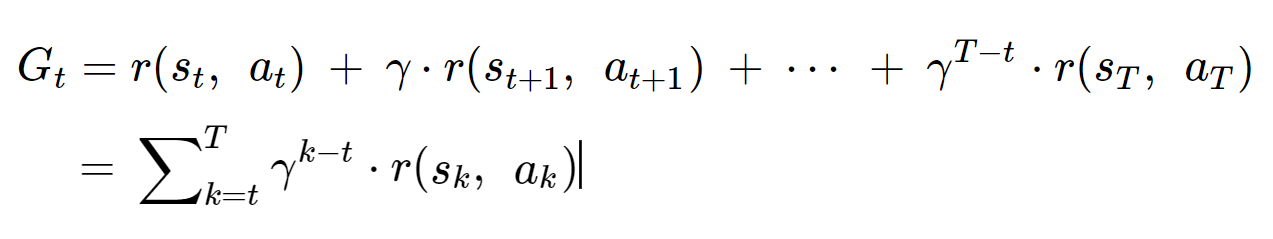
gamma는 미래의 보상을 얼마나 고려할 것인지를 의미하는 상수이다.
gamma는 0 ~ 1 사이의 값이며, gamma가 [0, 1) 구간에 속할 때 다음 식이 성립한다.
T가 무수히 커져도 반환값은 발산하지 않게 된다.
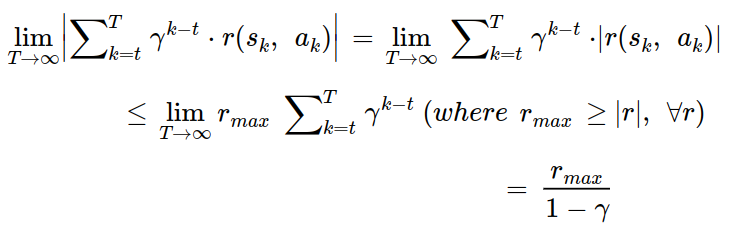
세번째 줄의 과정은 다음 식에 의해 정리되는 것이다.
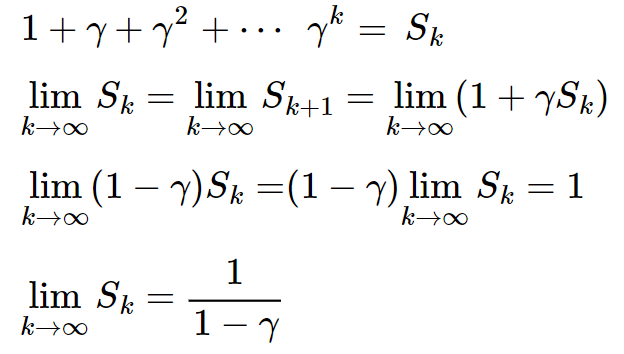
상태 가치 함수
반환값의 정의를 하였으니, 상태가치함수를 정의할 수 있다.
상태 가치 함수는 현재 state에서 기대할 수 있는 반환값의 기댓값이다.
상태 가치 함수를 수식으로 정리하면 다음과 같다.
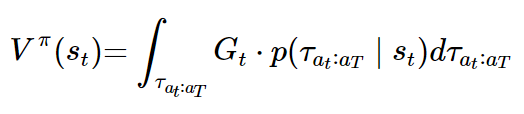
tau의 밑첨자 a_t:a_T는 행동 a_t부터 마지막 행동 a_T까지의 궤적을 나타낸다.
s_t가 조건부로 들어가고, 모든 궤적에 대해 기댓값을 계산한다고 이해하면 된다.
또한 G_t가 t의 함수로 보이지만, 사실상 궤적에 대한 함수이다. (왜 그런지는 위의 반환값 수식을 보고 이해할 수 있다.)
행동 가치 함수
행동 가치 함수는 현재 action에서 기대할 수 있는 반환값의 기댓값이다.
행동 가치 함수는 다음과 같다.
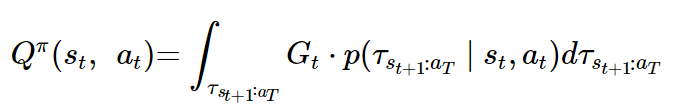
행동 가치 함수도 상태 가치 함수와 비슷하게 이해하면 된다.
tau의 밑첨자인 s(t+1):a_T는 a_t를 하고 난 상태인 s(t+1)부터 마지막 행동 a_T까지의 궤적을 의미한다.
우리는 상태 가치 함수와 행동 가치 함수를 정의함으로써 의미있는 관계를 유도해볼 수 있다.
(1) 상태 가치 함수와 행동 가치 함수의 관계
먼저 식을 유도해보기 전에 마르코프 프로세스에 대해서 이해하고 있어야 한다.
마르코프 프로세스는 특정 시점 t에서 k>t의 사건과 s<t의 사건이 독립일 때, 다음 식이 성립하는 것을 의미한다.
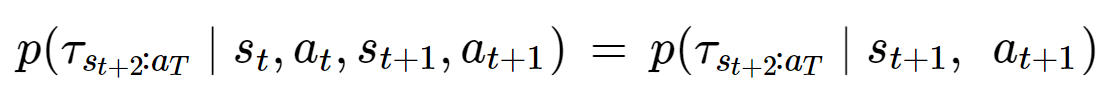
s_(t+1)이 s_t와 a_t의 정보를 내포하고 있다는 것을 의미하기도 한다.
t와 t+2는 독립이기 떄문에, t항들을 없애도 문제가 없는 것이다.
그러면, 상태 가치 함수와 행동 가치 함수의 관계를 유도해보자.
먼저 베이즈 정리에 의해 다음 식이 성립한다.
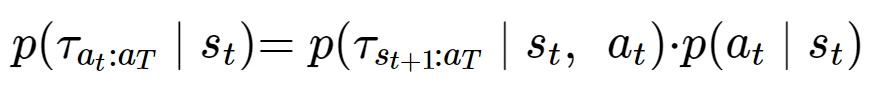
그럼 다음과 같이 상태 가치 함수를 바꾸어 써볼 수 있다.
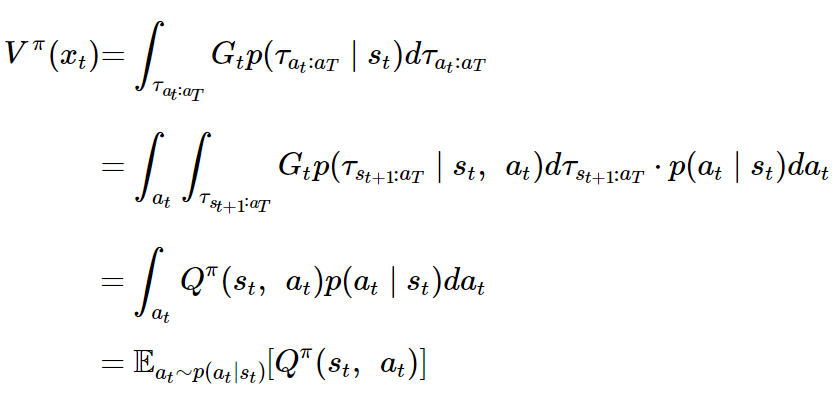
유도를 하고 보니 t에서의 상태가치함수는 t에서의 Q의 기댓값과 같다.
다음은 상태가치함수를 시간스텝 t+1에서의 상태가치함수로 표현해보록 할 것이다.
(2) V와 next V의 관계
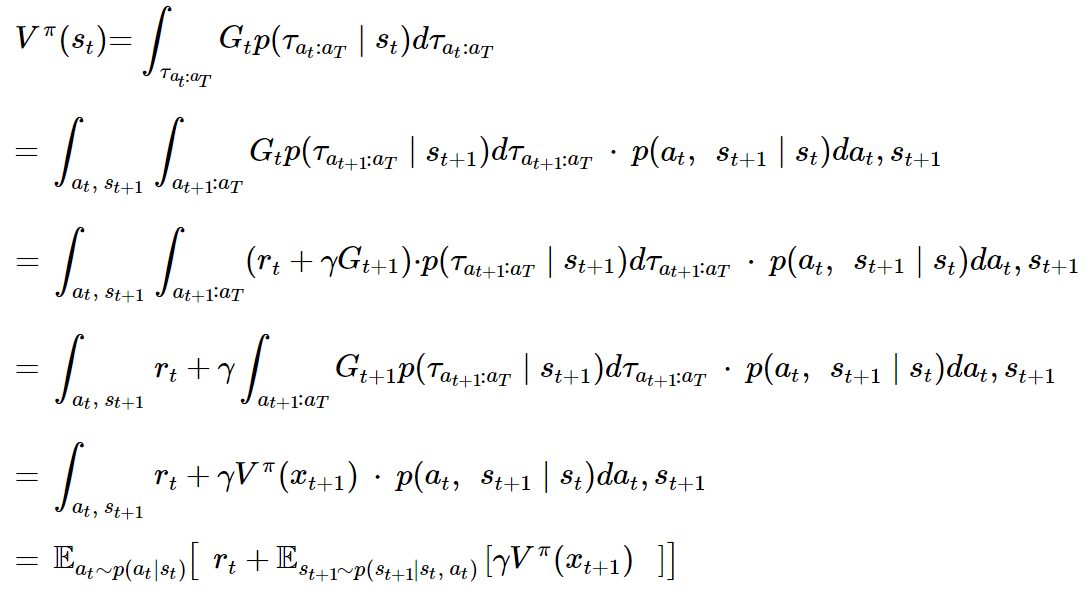
두번째 줄에서 s_t, a_t는 마르코프 프로세스에 의해 없어졌다.
또한 네번째 줄에서 r_t는 t의 함수이기 때문에 t+1 ~ T의 적분기호를 빠져나올 수 있다.
그렇게 V와 next V의 관계에 대해서도 식으로 정리해볼 수 있었다.
그리고 사실 이 식을 벨만 방정식이라고 부른다. 벨만 방정식은 상태가치함수와 행동가치함수 모두 있지만, 본 글에서는 상태가치함수만 다루었다. 관계 (1)과 (2)를 활용하여 행동가치함수의 벨만 방정식 또한 쉽게 구해볼 수 있다.
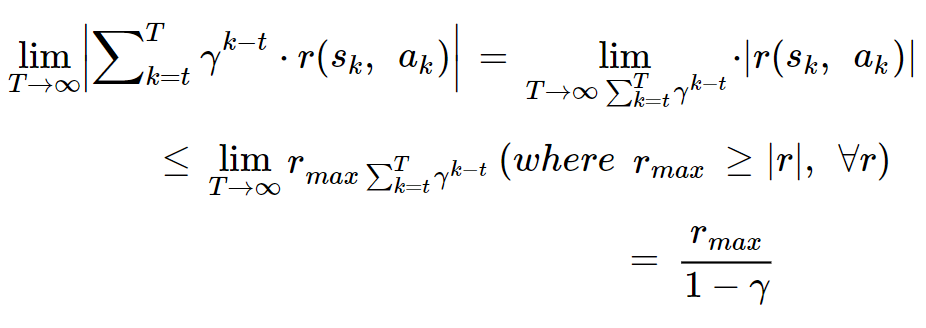
잘 봤습니다. 좋은 글 감사합니다.