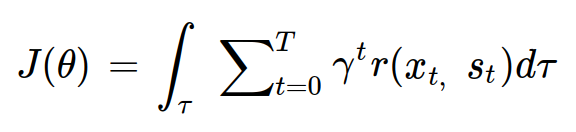이전 글에서는 상태 가치 함수와 행동 가치 함수, 벨만 방정식에 대해 알아보았다.
본 게시글에서는 정책(policy)를 parameterized하여 학습하는 방법에 대해서 알아볼 것이다.
목적함수의 정의
먼저 모델을 최적화하기 위해서는 비용함수나 목적함수가 정의되어야 한다.
정책 그래디언트에서는 다음과 같이 목적함수를 정의한다.
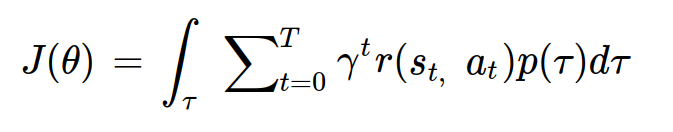
모든 궤적에 대해 반환값의 기대값을 계산한 값이 목적함수의 함숫값이다.
tau를 s_0과 a_0:a_T로 나누면 다음과 같이 정리할 수 있다.
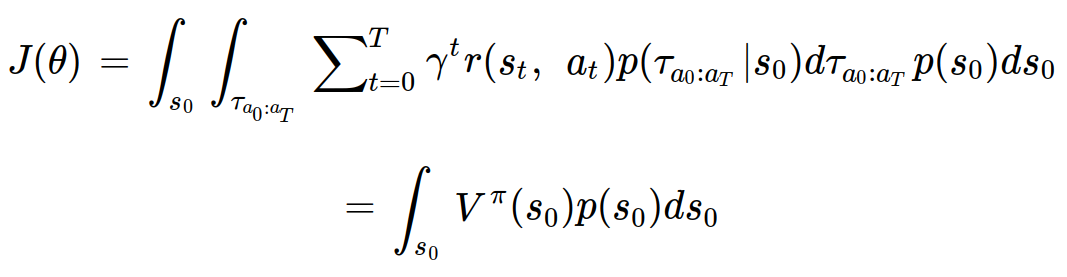
초기상태 s_0에 대해서 상태 가치 함수의 기대값을 구한 것과 같다. 이렇게 목적함수의 의미까지 직관적으로 이해해볼 수 있었다.
최적화를 통하여 모델을 학습시키기 위해서는 목적함수를 알맞게 미분하는 것이 중요하다.
목적함수의 미분
p(tau)를 다음과 같이 정리할 수 있다.
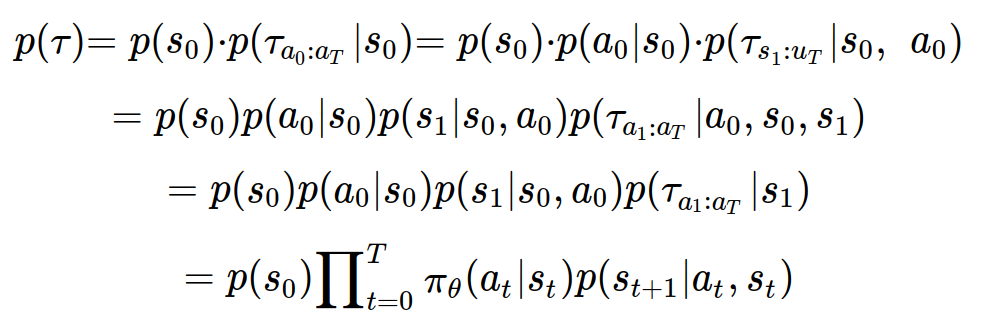
세번째 줄에서는 마르코프 프로세스에 의해 a_0과 s_0가 없어진 것이다. pi_theta는 theta로 parameterized된 정책(policy)를 의미한다.
목적함수를 가중치 theta에 대해서 미분하면 다음과 같다.
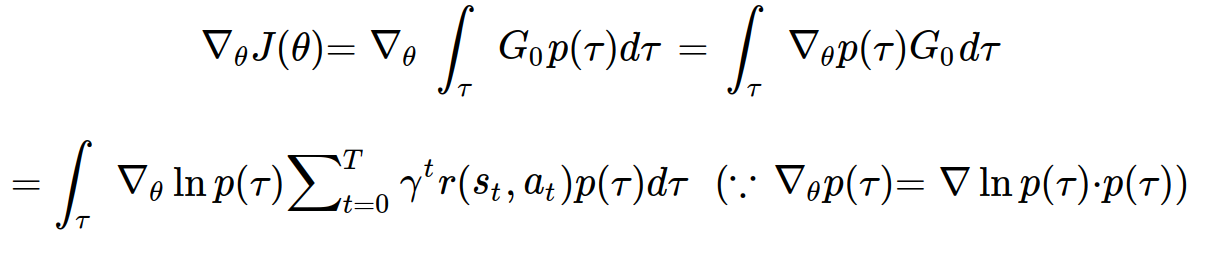
gradient_theta ln(p(tau)) 부분만 정리해보면 다음과 같이 정리할 수 있다.
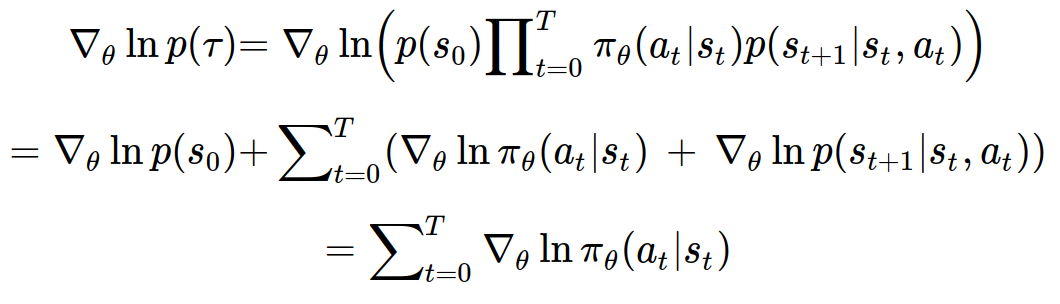
theta에 대한 함수는 정책(policy) 밖에 없기 때문에 위와 같이 정리되는 것이다.
다시 위의 식을 목적함수의 미분식에 대입하면 다음과 같다.
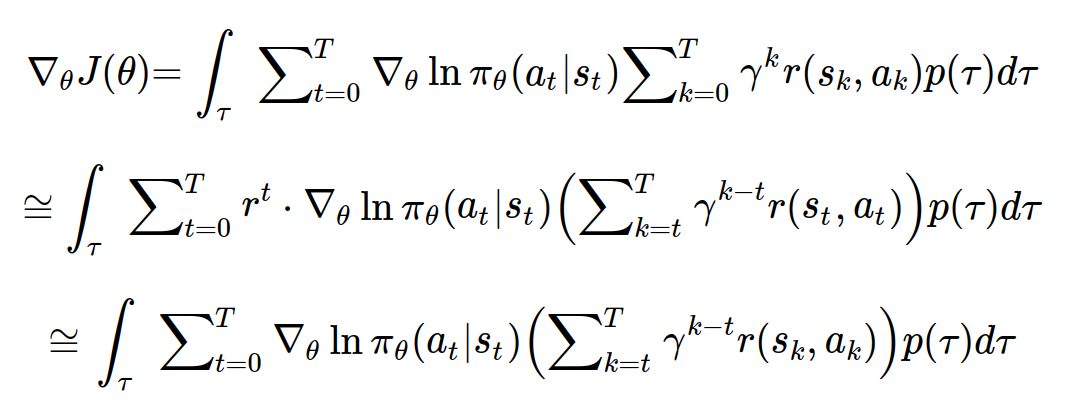
시간스텝 t에서의 정책과 k<t에서의 반환값은 서로 영향을 줄 수 없기 때문에, (인과성이 없기 때문에) 두번째 줄과 같이 식을 고쳐줄 수 있다.
하지만, 두번째 줄처럼 사용하게 되면 T가 아주 커질수록 미분값이 0에 수렴하므로 에피소드의 후반부에 있는 미분값을 무시하는 경향이 커질 수 있다. 최종적으로는 r^t를 없애어 근사적으로 미분을 할 수 있다.
REINFORCE 알고리즘
목적함수와 목적함수의 미분을 다시 써보면 다음과 같다.
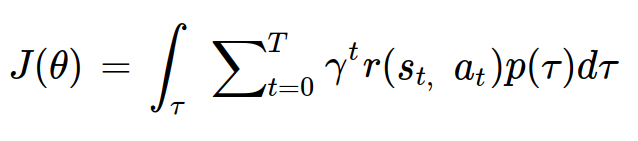
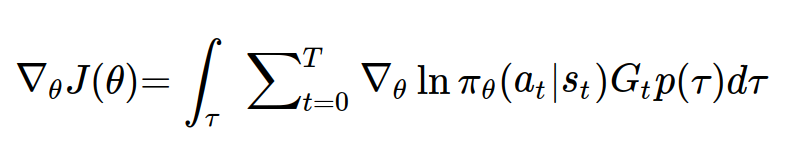
실제 학습을 시킬 때는 모든 궤적에 대해서 목적함수의 미분값을 구하는 것이 힘들기 때문에 sampling 기법을 이용하여 간단하게 정리할 수 있다. iid 분포로 sampling된 데이터들은 원래 분포를 근사할 수 있다는 가정이 전제된다.
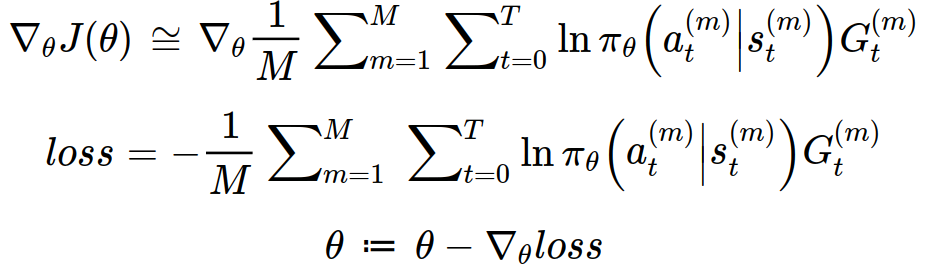
위와 같은 방법으로 정책 그래디언트를 활용하여 알맞은 정책을 구할 수 있다.
REINFORCE 알고리즘의 한계
REINFORCE 알고리즘은 크게 3가지의 한계점을 갖고 있다.
- 그래디언트의 값이 반환값에 따라 크게 변하는데, 이로 인하여 그래디언트의 분산이 너무 커서 학습이 불안정해진다.
- 업데이트 주기가 많이 길다. 업데이트 주기를 가장 짧게 하여도, 에피소드 한번이 끝나야 업데이트 한번을 할 수 있다. (반환값을 계산해야 하기 때문이다.)
- 정책을 업데이트하기 위해서 해당 정책을 실행시켜 발생한 샘플이 필요한 on-policy 방법을 사용하여 효율성이 떨어진다.
위와 같은 3가지의 한계점으로 인해 현재는 REINFORCE 알고리즘이 잘 사용되고 있지 않다.
다음 글에서는 (1)과 (2)의 한계점을 개선시킨 A2C에 대해서 알아볼 것이다.