참고 - https://youtu.be/RGB-wlatStc
항상 감사한 인도선생님..^^

Basics

Bresenham 알고리즘은 기울기가 1 이하인 선에 적용 가능하다.
(알고리즘을 조금만 변경하면 1 이상의 선에도 적용 가능)

화면은 픽셀의 집합이다.
따라서 직선의 방정식은 적합하지 않고, Raster라는 것을 사용한다. (Rasterization)

직선을 그리기 위해 직선의 방정식에서 좌표들을 얻어야 한다.
우리가 필요한 값은 x, y 값이다. 하나의 식에서 두 값을 얻으려면 샘플링이라는 것을 해야한다.
-> Δx는 Δy보다 크기 때문에, 선의 좌표값에 있어서 모든 x는 각기 다른 값을 갖게 된다는 사실을 알 수 있다.
(기울기가 1 보다 작은 경우, x값은 항상 증가하지만 y값은 아님)

Drawback of DDA

DDA?

DDA는 실수값을 사용한다.
하지만 픽셀은 정수로 이루어져 있기 때문에, 실수값을 피하기 위해 Bresenham 알고리즘을 사용한다.

Derivation of Bresenham

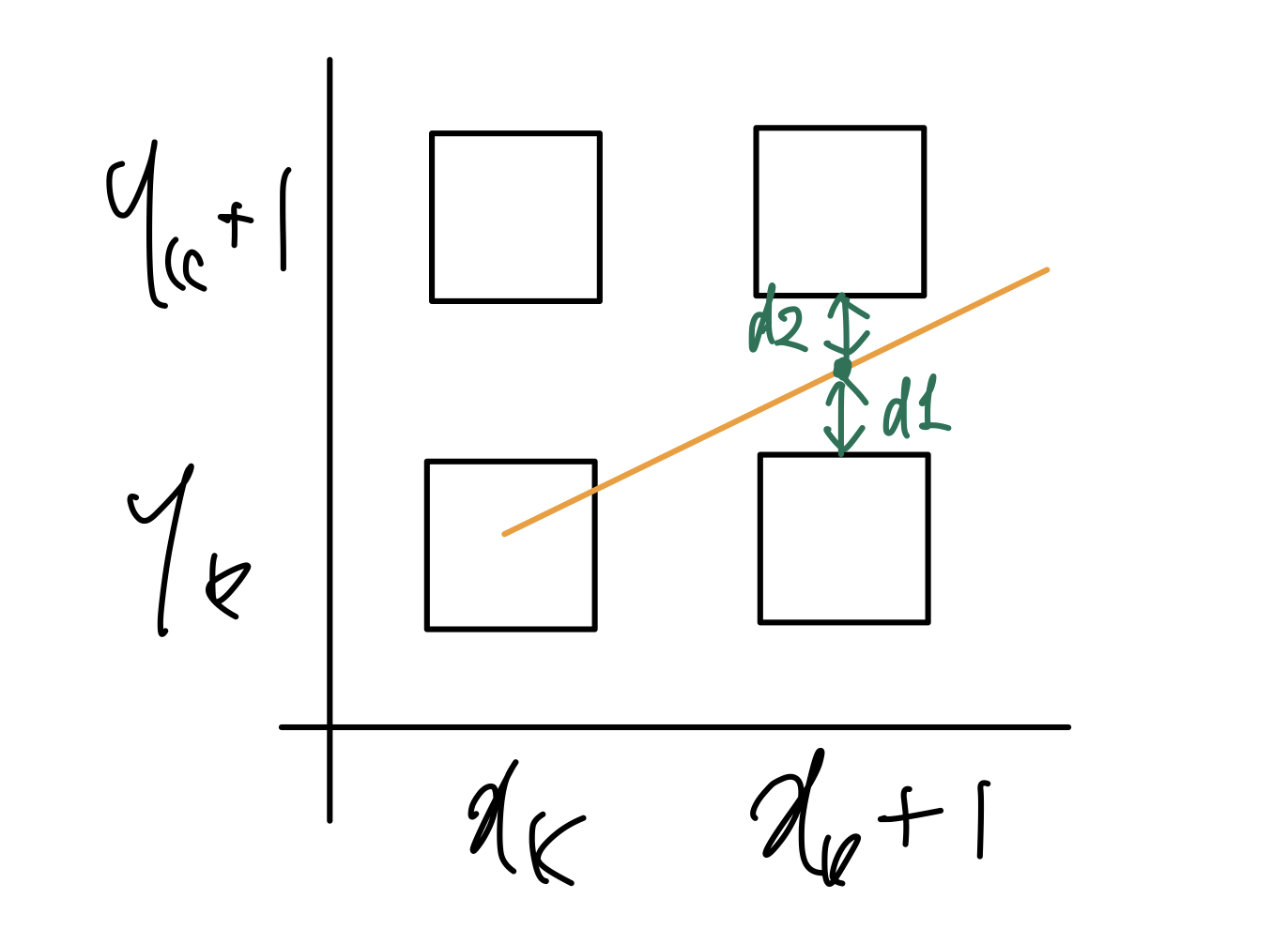
위와 같은 상황에서 두 픽셀 중 어느 픽셀을 선택해야 할까?
직선과의 거리를 비교하여 가까운 쪽을 선택한다.

좌표값은 다음과 같이 얻어진다.

좌표값으로 식을 유추할 수 있다.

따라서 d1, d2를 아래처럼 얻을 수 있다.
$d_1 = y - y_k = m(x_k + 1) + C - y_k$
$d_2 = y_k + 1 - y = y_k + 1 - [m(x_k + 1) + C]$

$d_1 - d_2$ 값이 양수이면 $y$값을 하나 증가시키고, 아니면 그대로 둔다.

$m$은 실수이므로 양쪽을 $Δx$로 곱해준다.

$2Δy, 2ΔxC, Δx$는 상수이므로 제거해주면 아래 식(결정 변수)이 나온다.

$P_k$를 이용하여 $P_{next}$를 구해보자.

따라서 $P_k < 0$ 이면, $P_{next} = P_k + 2Δy$ 이고,
$P_k \geq 0$ 이면, $P_{next} = P_k + 2Δy - 2Δx$ 이다.

What should be Initial Value of $P_k$?

이제 $P_k$의 초기값($P_1$)을 구해봅시다.

$y = mx + C$를 이용해서 C를 구한다. $C = y_1 - \dfrac{Δy}{Δx}x_1$

Bresenham 알고리즘 구현

위에서 구한 두가지 식을 이용해서 bresenham 알고리즘을 구현해보자.

void Bresenham(x0, y0, x1, y1)
{
	x = x0;
    y = y0;
    dx = x1 - x0;
    dy = y1 - y0;
    P = 2dy - dx;  // P1(초기값) 설정
    while (x <= x1)
    {
    	putpixel(x,y);
        x++;  // x는 매 좌표마다 증가
        if (P < 0)  // Pnext 구하는 부분
        	P = P + 2dy;
        else
        {
        	P = P + 2dy - 2dx;
            y++;
        }
    }
}

모든 기울기에 대해 적용해보자

https://en.wikipedia.org/wiki/Bresenham%27s_line_algorithm#All_cases
위 링크의 All cases 부분을 참고하면 쉽게 구현 가능하다.
요약해보면,
(x0, y0, x1, y1) 네 가지 매개변수를 이용해서 흐름이 나뉜다.
1. dy의 절대값과 dx의 절대값을 비교해서 호출할 함수를 결정한다.
2-1. dx의 절대값이 큰 경우 x0과 x1을 비교해서 인수 순서를 달리 한다.
2-2. dy의 절대값이 큰 경우 y0과 y1을 비교해서 인수 순서를 달리 한다