[자료구조] 스택(Stack)

개발잘하기프로젝트·2020년 11월 10일

자료구조 & 알고리즘 시리즈

목록 보기

4/7

🤔 스택(Stack)?

스택(Stack)은 데이터를 제한적으로 접근 할 수 있는 구조이다. 한쪽 끝에서만 자료를 넣거나 뺄 수 있는 구조로 이러한 점은 큐(Queue)와 마찬가지이다. 하지만 큐(Queue)와 다른 점은 가장 나중에 쌓은 데이터를 가장 먼저 빼낼 수 있는 데이터라는 점이다.

스택(Stack)의 구조와 용어?

스택(Stack)은 큐(Queue)와 다르게 LIFO (Last-in, First-out) 또는 FILO (First-In, Last-Out)의 데이터 관리 방식을 따른다. 마치 책을 쌓는 것과 유사하다. 책을 순차적으로 바닥에서 쌓아 올리고 다시꺼낼 때 가장 나중에 올린책을 먼저 집어야 그 다음의 책을 꺼낼 수 있다. 대표적인 스택의 활용은 컴퓨터 내부의 프로세스 구조의 함수 동작 방식이다. 스택의 주요기능은 push(), pop() 메서드처럼 데이터를 스택(Stack)에 넣거나 꺼내게 된다.

LIFO (Last-In, First-Out)
후입선출이라고 한다. 마지막에 넣은 데이터가 가장 먼저 나온다.

FILO (First-In, Last-Out)
처음에 넣은 데이터가 가장 나중에 나온다.

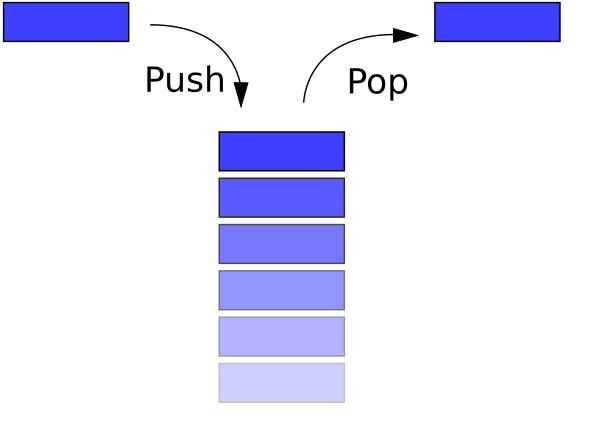
스택(Stack)에 데이터를 넣는 것을 Push라고 하고 데이터를 꺼내는 것은 Pop이라고 한다. 스택 구조는 프로세스 실행 구조의 가장 기본이 된다. 함수 호출 시 프로세스 실행 구조를 스택과 비교해서 이해할 수 있다.

// 재귀 함수
function recursive(data) {
  if (data < 0) {
    console.log('ended');
  } else {
    console.log(data);
    recursive(data - 1);
    console.log('returned', data);
  }
}

recursive(4);

스택(Stack)의 장점과 단점?

스택(Stack)의 장점은 데이터 구조가 단순해서 구현하기가 쉽다. 그리고 데이터를 저장하거나 읽는 속도가 빠르다. 스택의 단점은 일반적인 스택 구현시 데이터의 최대 갯수를 미리 정해야 한다. Python의 경우 재귀함수는 1,000번까지만 호출이 가능하다. 이 뜻은 1,000번을 호출할 수 있는 공간을 미리 확보를 해두었다는 것과 같다. 즉, 데이터 저장 공간의 낭비가 발생할 수 있다.

스택은 단순하고 빠른 성능을 위해 사용되므로 보통 배열 구조를 활용해서 구현하는 것이 일반적이다. 이런 경우에는 앞에서 말한 단점이 있을 수 있다.

Javascript에서의 스택(Stack)?

Javascript에서 스택(Stack)을 Class로 구현하면 다음과 같다.

class Stack {
  #array; // private

  constructor(array = []) {
    if (!Array.isArray(array)) {
      throw new TypeError(`${array} is not an array.`);
    }
    this.#array = array;
  }

  push(value) {
    return this.#array.push(value);
  }
  pop() {
    return this.#array.pop();
  }
  entries() {
    return [...this.#array];
  }
}

const stack = new Stack([1, 2]);
console.log(stack.entries()); // [1, 2]

stack.push(3);
console.log(stack.entries()); // [1, 2, 3]

stack.pop();
console.log(stack.entries()); // [1, 2]