
출처: YOUTUBE: Learn the Math behind Odometry | Essence of Robot Odometry Pt. 2 - Rex Liu
Odometry Algorithm

오도미터 추적 알고리즘의 핵심은 추적 휠을 사용하여, 로봇의 두 벡터, 즉, 위치 벡터 d와 방향 벡터 θ에 대한 실시간 데이터를 제공하는 것.
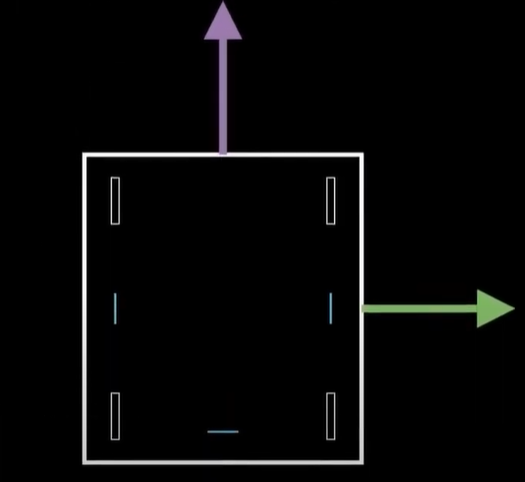
위치 벡터는 로봇이 필드에서 정확히 어디에 있는지 알려주고,
방향 벡터는 필드를 기준으로 로봇이 어디를 향하고 있는지 나타냄.
해당 두 벡터를 구하기 위해, 로봇의 동작을 하단과 같이 '호'로 모델링하기로 함.
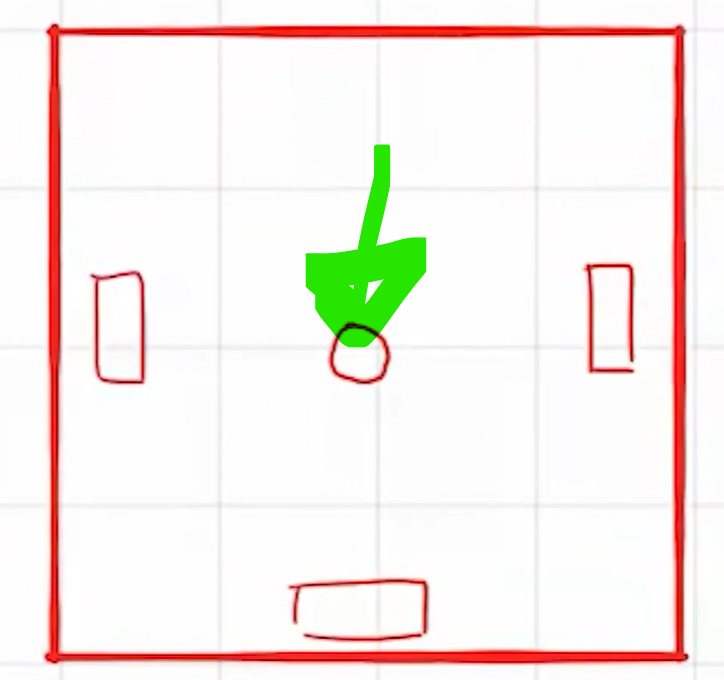
상단 상자를 우리의 bot이라고 하자. 해당 제품에는 추적 휠 3개와 추적 센터가 있음.
모든 측정은 해당 추적 센터(초록색)를 기준으로 수행됨.
즉, 필드를 따라 움직이는 로봇 전체를 추적하는 대신, 해당 지점만 추적하는 데 집중하게 됨.
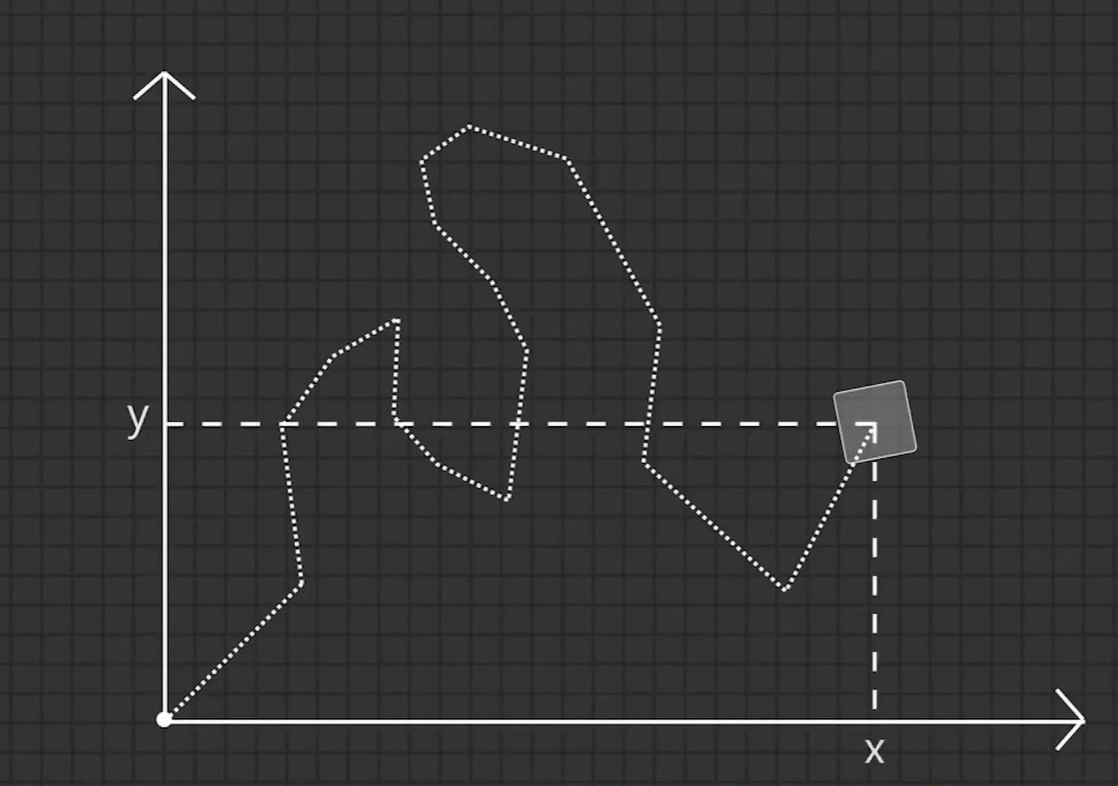
일반적으로, 추적 센터는 bot의 중심이라고 생각하면 됨.
실제로 수학에 영향을 미치는 것은 추적 휠(=휠의 배치)이고, 가장 주의를 기울여야 할 부분임.
<추적 휠 배치 시 주의해야 할 3가지 규칙>
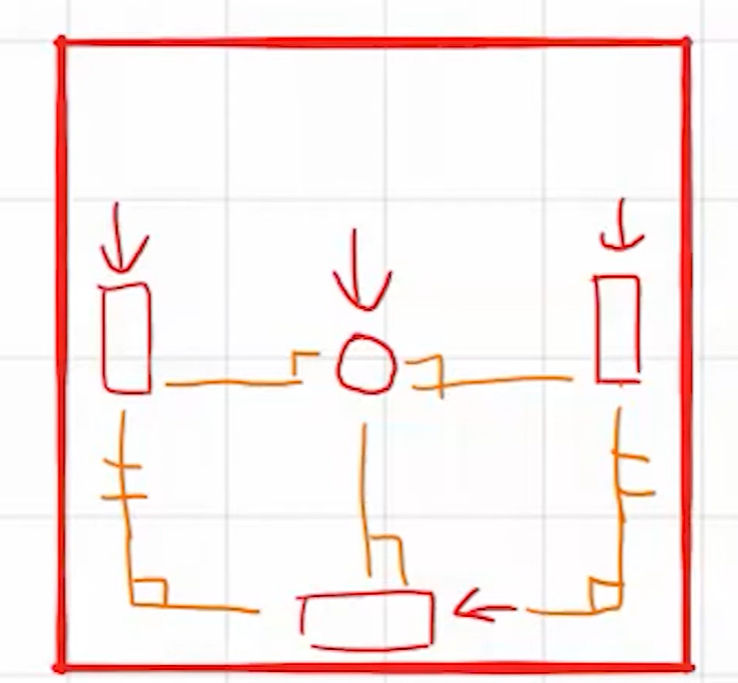
(1) 모든 추적 휠(왼/오/뒤)이 추적 센터로부터 수직이어야 함.
(2) 왼쪽과 오른쪽 추적 휠은 서로 평행해야 함.
(3) 백 트래킹 휠은 좌우 트래킹 휠과 수직이어야 함.
이 세 가지 배치 규칙을 모두 따르면, 오도미터 알고리즘을 수학적으로 작동할 수 있음.
세 개의 추적 휠을 배치하는 방법은 하단과 같이 다양함.
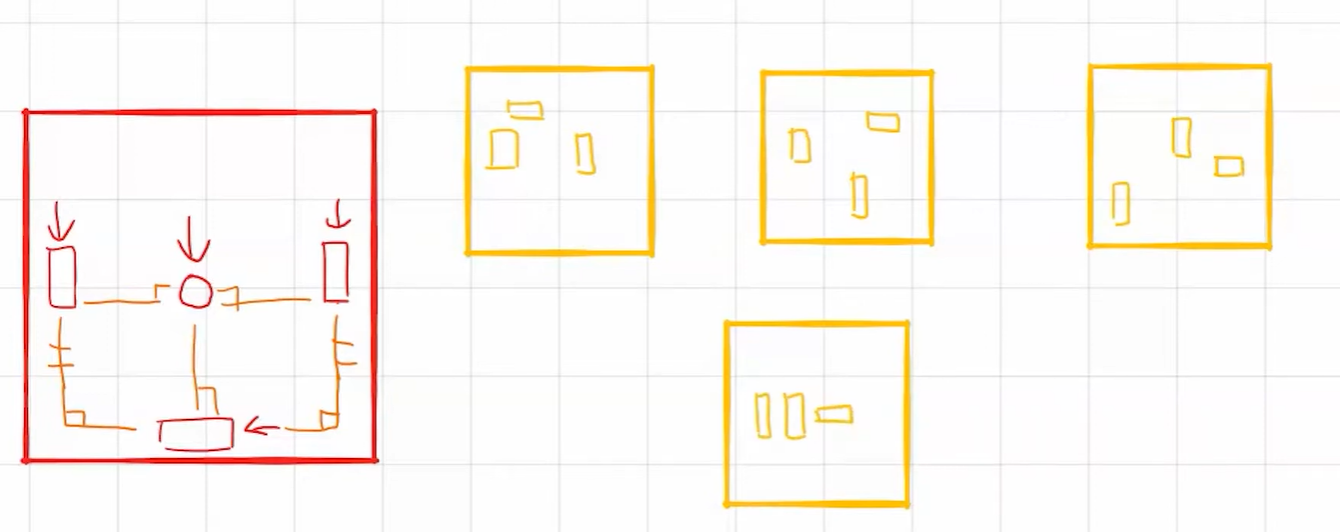
일단 간단하게 추적 휠을 하단과 같이 배치하고자 함.
왼쪽 추적 휠과 오른쪽 추적 휠 사이의 거리와 추적 중심 사이의 거리가 같도록 설정.
로봇 상수(위치/방향 벡터 계산 시 고려)
Tl = 왼쪽 추적 휠~추적 센터, 7.250인치
Tr = 오른쪽 추적 휠~추적 센터, 7.250인치
Tb = 추적 중심으로 향하는 백트래킹 휠, 7.750인치
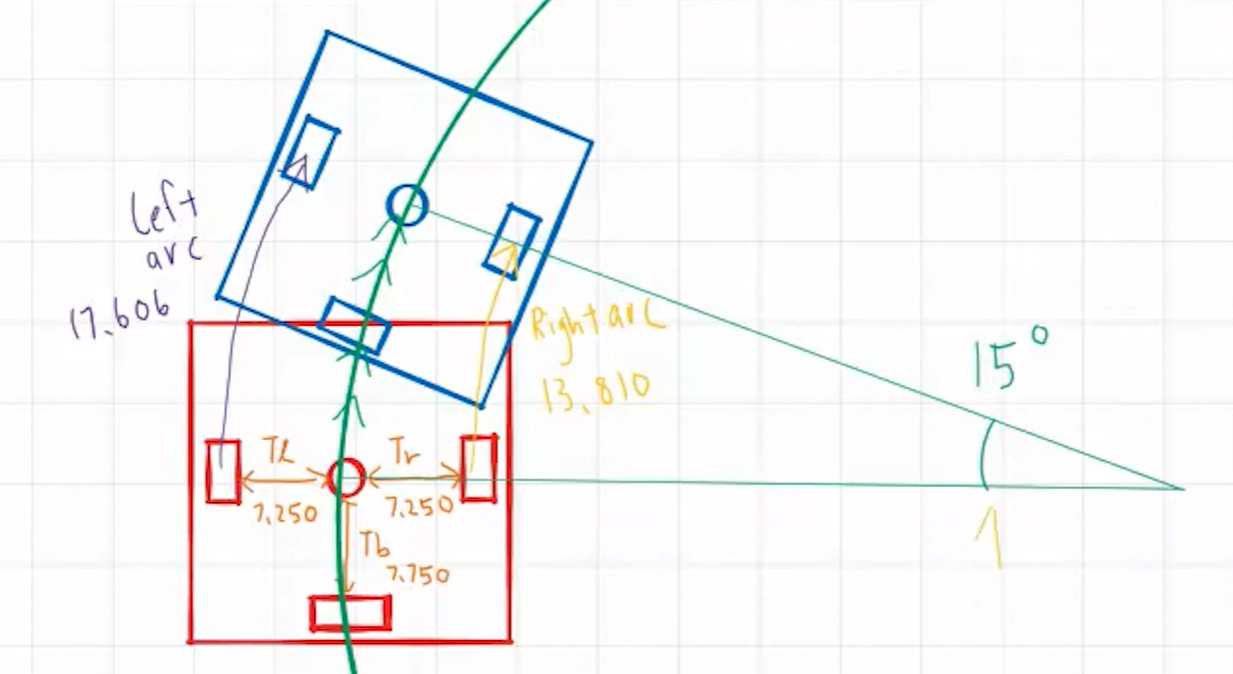
빨간색에서 파란색으로 로봇이 움직인다고 했을 때, 이 두 추적 중심을 통과하는 원을 그리고자 한다. 그렇게 되면, 실제로 15도 각도로 따라가는 것을 볼 수 있음.
왼쪽 추적 휠이 통과하는 바깥쪽 호를 '왼쪽 호'라고 하고 17.606인치임.
오른 추적 휠이 통과하는 안쪽 호를 '오른쪽 호'라고 하고 13.810인치임.
호의 중심 각도는 실제 로봇의 새로운 방향과 같은 각도임.
따라서, 추적 중심의 호에 대한 각도만 계산할 수 있다면, 실제로 로봇의 새로운 위치에서 방향을 파악할 수 있음.
각도 계산을 위해서는?
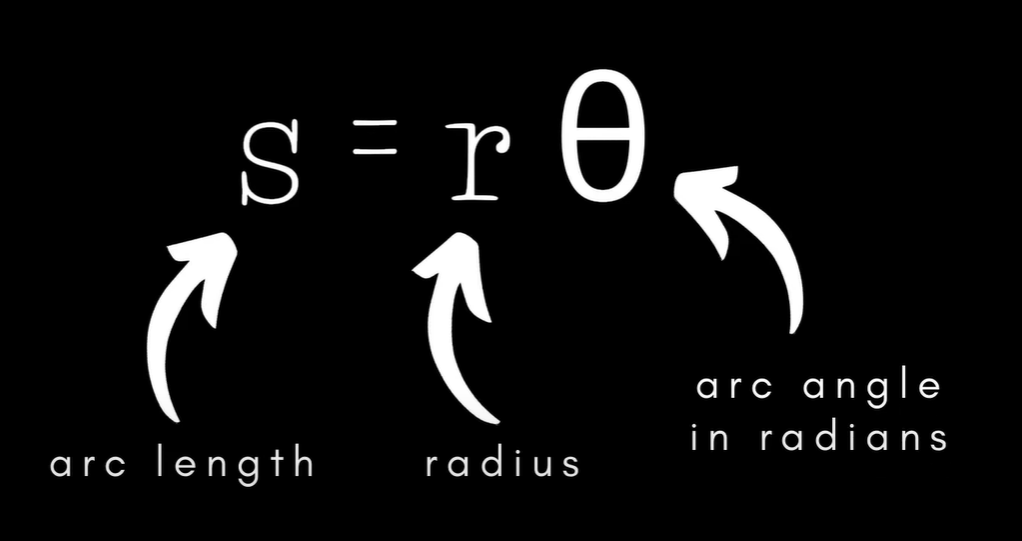
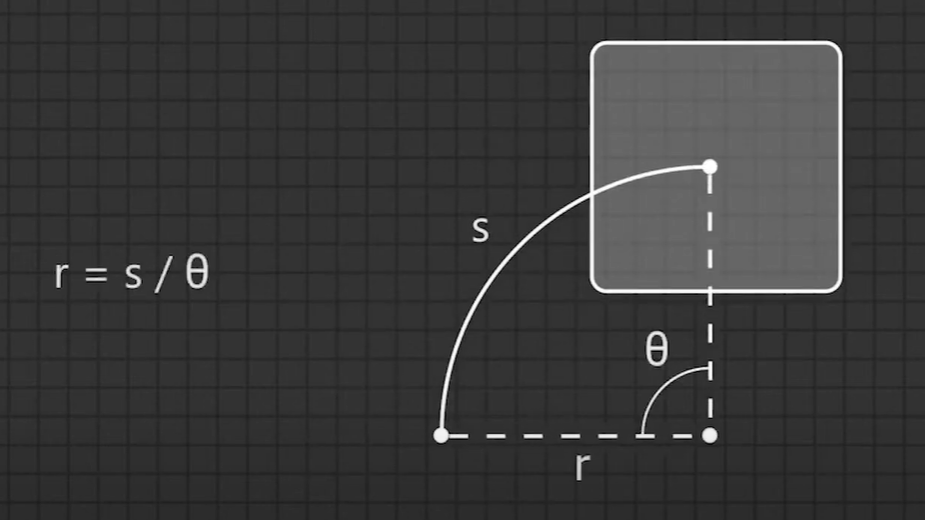
호 길이 공식을 통해 시작.

(라디안 세부 설명)
이동한 호의 각도를 계산하려면, 좌우 호를 구성하는 추적 휠의 정보를 사용해야 함.
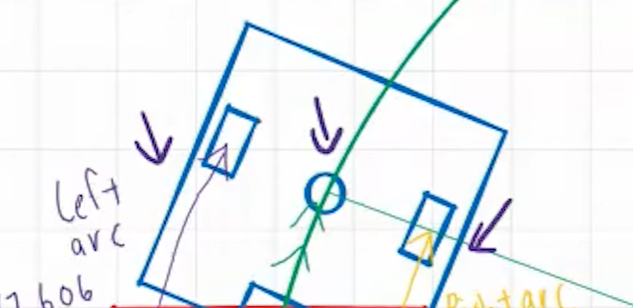
세 개의 호(보라색 화살표)는 모두 호의 각도가 같음. 원의 같은 중심을 공유하기 때문(반경이 다를 뿐).
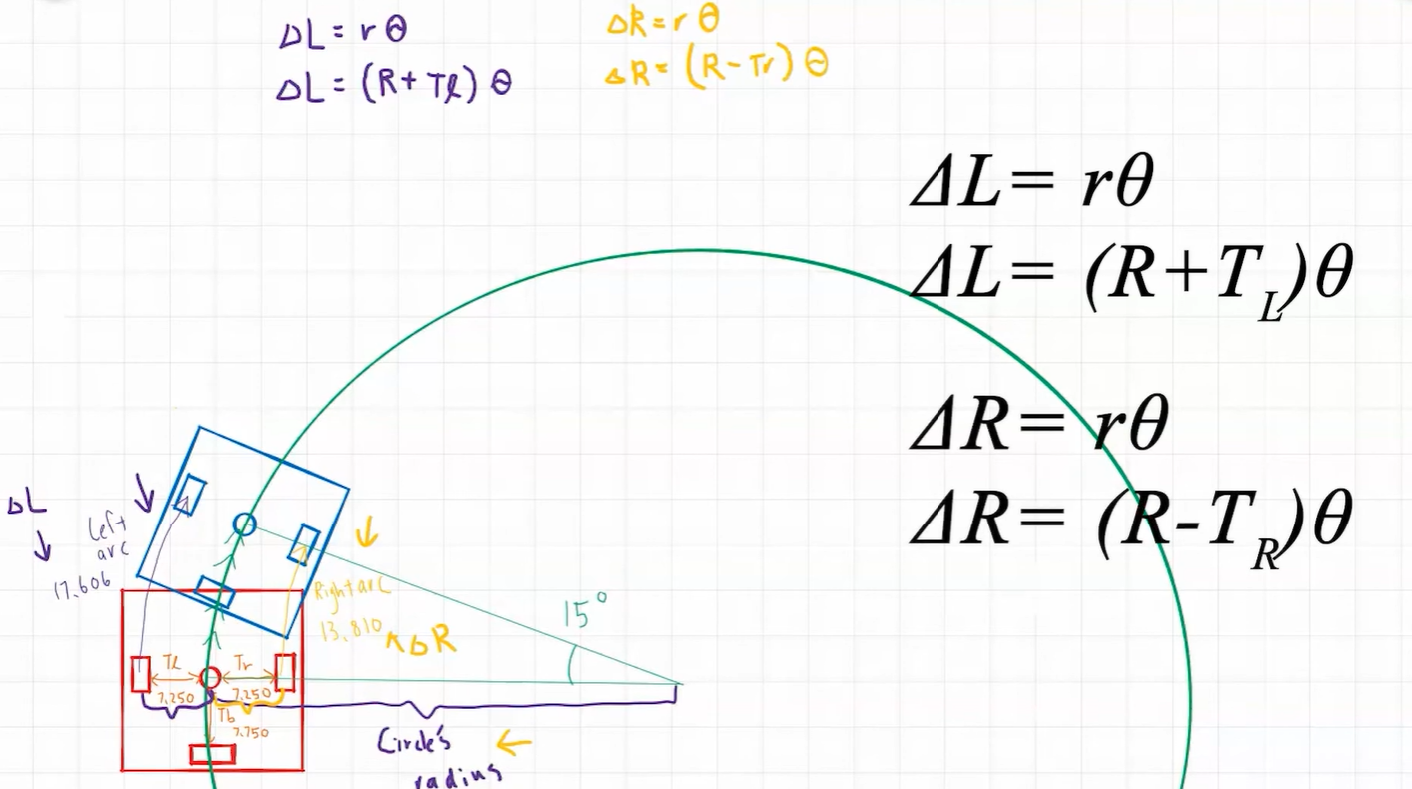
델타 L은 왼쪽 호의 호 길이와 동일하고, 이전의 호 길이 공식을 사용하면 호의 길이는 반지름에 각도를 곱한 값임을 알 수 있음.
델타 L은 왼쪽 호의 반지름과 같고, 왼쪽 호는 원의 반지름(R)과 Tl을 더한 값과 같음. 이걸 세타로 곱하면 호 각도는 델타 L과 같게 됨.
오른쪽도 같게 구성하여, 델타 R에 대한 값을 구할 수 있음.

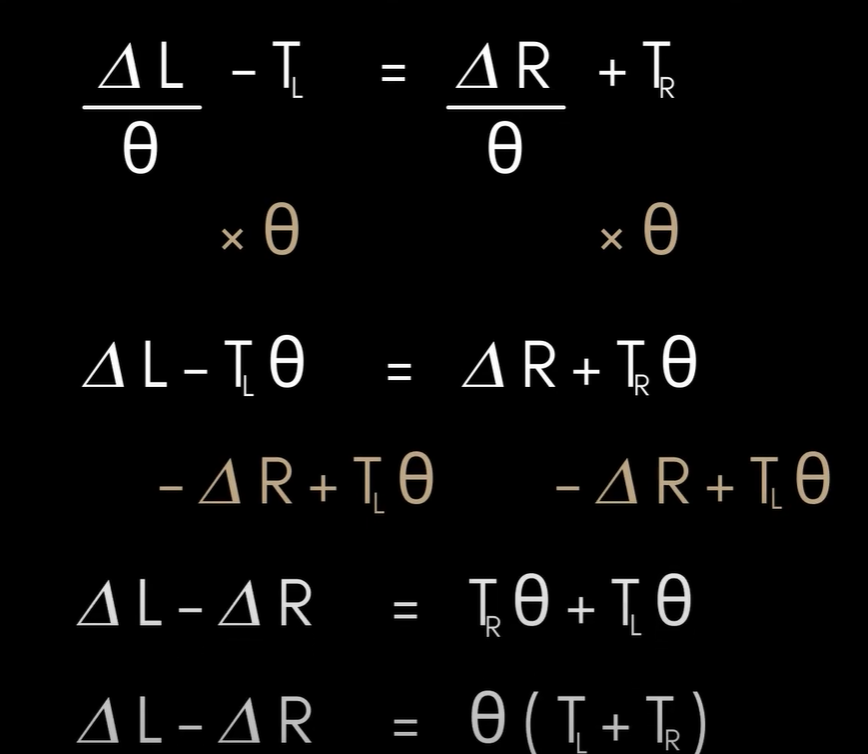
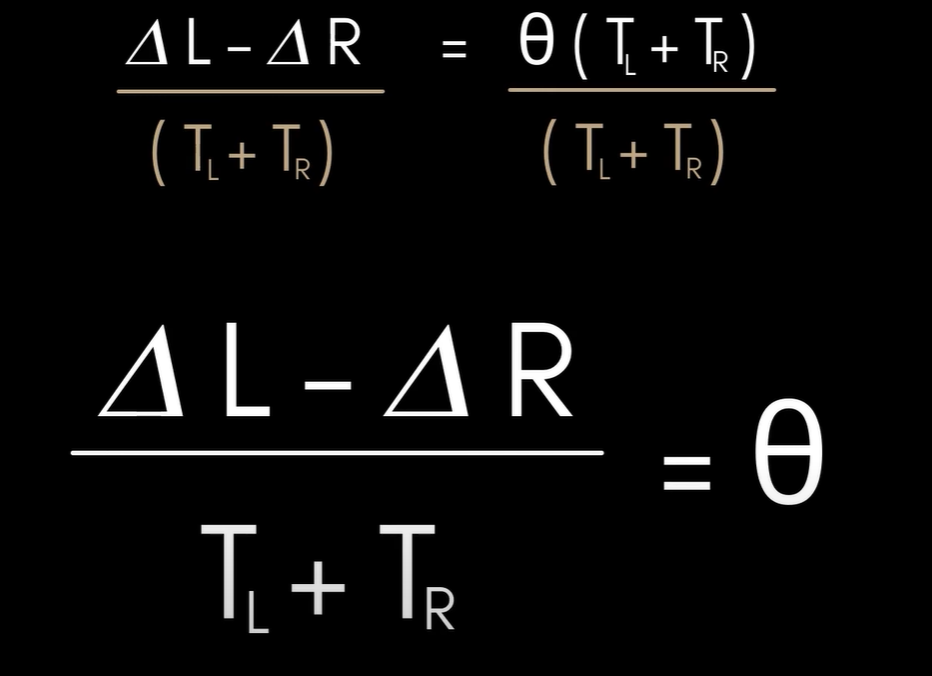
이렇게 추적 휠을 사용하여, 로봇의 순간적인 방향을 계산하는 방정식을 도출해냄.
즉, 추적 휠이 얼마나 움직였는지 알고 있다면, 필드 어디에서든 로봇의 방향을 찾을 수 있음.
로봇의 동작은 단순 여러 개의 호가 합쳐진 것일 뿐.
이전 방향에 따라 상대적 방향을 계산하는 대신, 이러한 절대적 양(델타 L, R)을 사용하여 로봇이 이전에 어떤 움직임을 했는지 관계 없이, 절대적 양으로 방향 계산 가능.
더불어, 과거 오류 조정 및 향후 움직임 수정 가능.
