[백준] 1463 - 1로만들기 (JAVA)

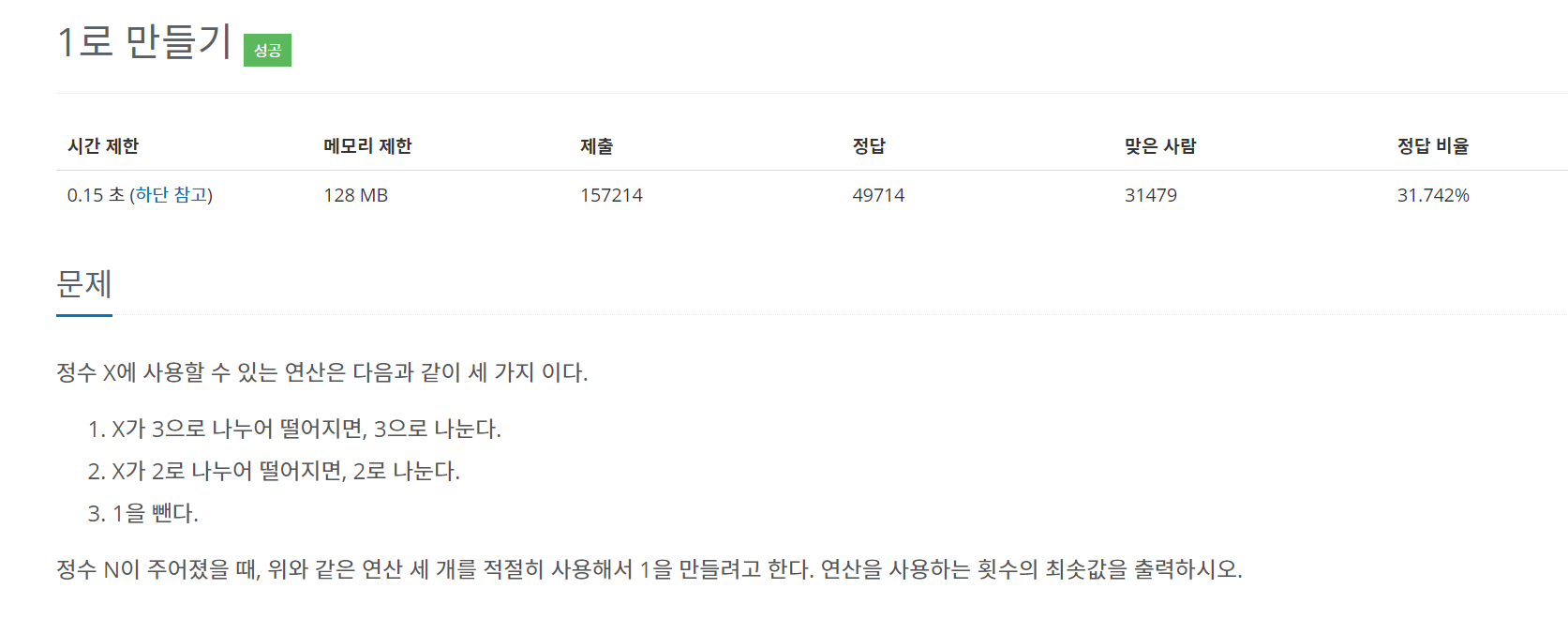
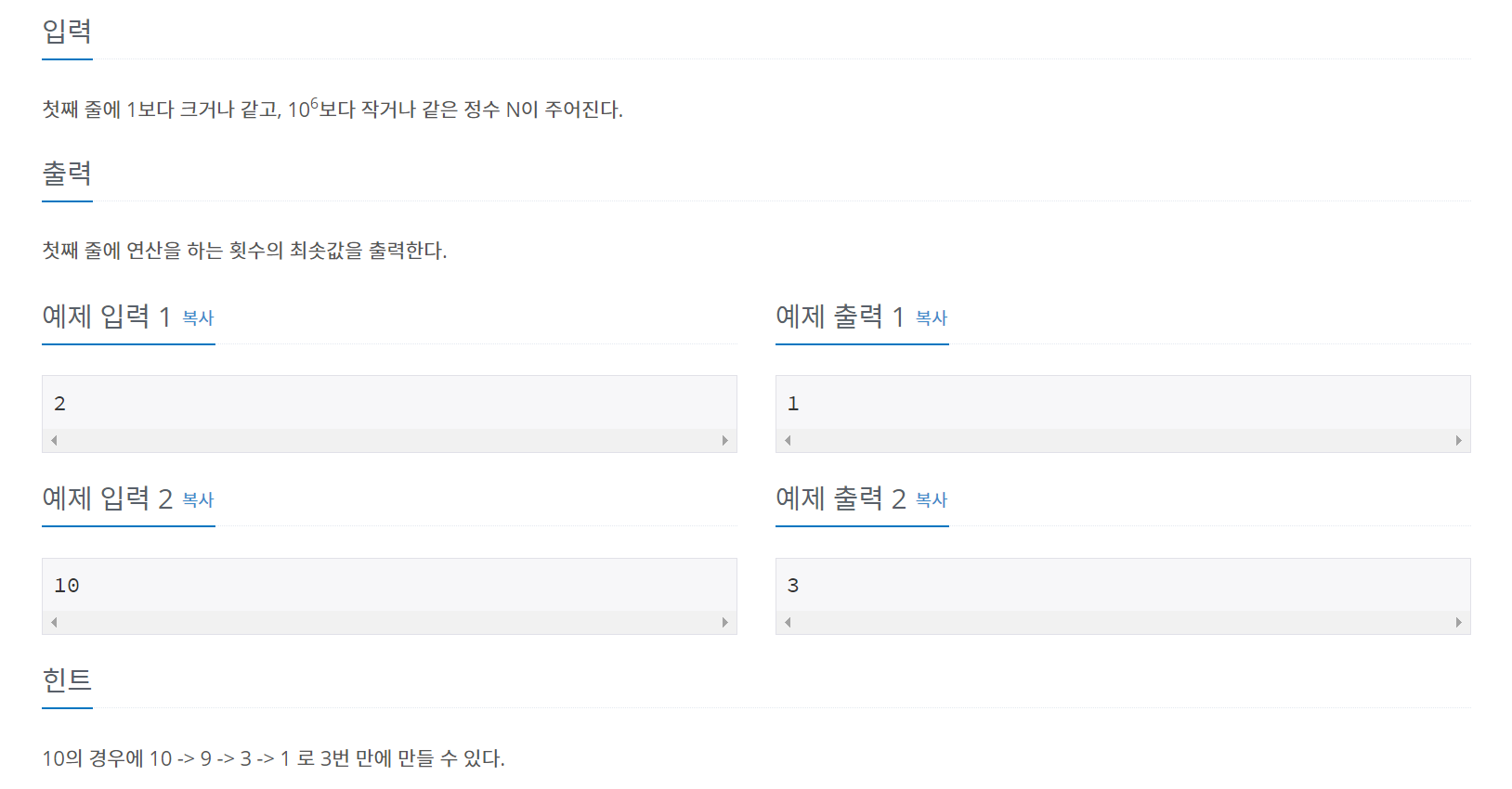
이 문제 푸느라 공책 5장은 쓴 것 같다...
DP는 너무 어렵다 ㅠㅠㅠ

처음에 생각한 것은 아래와 같다

1. 3으로 나누어떨어지면 3으로 나누고 다시 재귀함수 호출
2. else if 2로 나누어떨어지면 2로 나눠 재귀함수를 호출한 결과와 1을 빼고 재귀함수를 호출한 결과 중 작은 것을 리턴
3. 3과 2로도 나누어 지지 않으면 -1을 한 후 재귀함수 호출

그런데 위 로직처럼 코드를 짜면 틀렸다고 한다. 왜냐하면 2와 3의 공배수인 6으로 나누어떨어지는 수는
1. 3으로 나누기
2. 2로 나누기
3. 1을 빼기
이 세가지 경우를 모두 비교해서 그중 가장 작은 것을 리턴해야 하기 때문이다.

처음에 나는 3으로 나누어떨어지는 수는 무조건 일단 나누는 것이 최선이라고 생각했지만, 먼저 1을 빼는 것이 더 효율적인 반례도 존재하기 때문에 3가지의 경우를 모두 고려해야한다.

그리고 재귀함수 호출시 이미 cnt를 계산한 숫자는 memo[]에서 그 값을 가져온다. (memoization)

import java.util.Scanner;

public class No1463_1로만들기 {
    static int[] memo ;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int x = scanner.nextInt();
        memo = new int[x+1];

        System.out.println(dp(x));
    }

    public static int dp (int n) {
        if (n==1) {
            return 0;
        } //1부터 bottom-up으로 count를 증가시키기 위해 
        
        if (memo[n]==0) { //처음 방문한 숫자이면
            if (n % 6 == 0) { //2와 3으로 모두 나누어떨어짐
                memo[n] = Math.min(dp(n / 3) + 1, dp(n / 2)+ 1); 
                //우선 3과 2로 나눈 결과중 더 작은 값을 memo[]에 저장
                return memo[n] =Math.min(memo[n],dp(n-1)+1);
                // 위에서 임시로 저장한 값과, -1을 한 결과 중 더 작은 값을 최종으로 memo[]에 저장하여 리턴
            } else if (n % 3 == 0) { //3으로만
                return memo[n] = Math.min(dp(n / 3) +1, dp(n - 1)+ 1);
            } else if (n % 2 == 0) {//2로만
                return memo[n] = Math.min(dp(n / 2)+1, dp(n - 1)+1);
            }
            //둘다 나누어지지 않아 -1을 해야하는 경우
            return memo[n] = dp(n - 1)+1;
        }
        else { //이미 계산한적 있는 숫자
            return memo[n];
        }

        }



}