카이제곱 분포와 검정

출처 : https://www.youtube.com/watch?v=_GrdeYtYLO4

카이제곱분포

1. 정의
   양의 정수 $k$에 대해 $k$개의 독립적이고 표준정규분포를 따르는 확률 변수 $X_1, X_2, ... X_K$를 정의하면 자유도 $k$의 카이제곱 분포는 확률변수($Q = \displaystyle\sum_{i=1}^{k} X_i^2$)의 분포이다.
2. 자유도
   몇개의 표준 정규분포 변수를 더한 것인가?
   자유도 계산 : (변수1의 그룹수-1)*(변수2의 그룹수 -1)
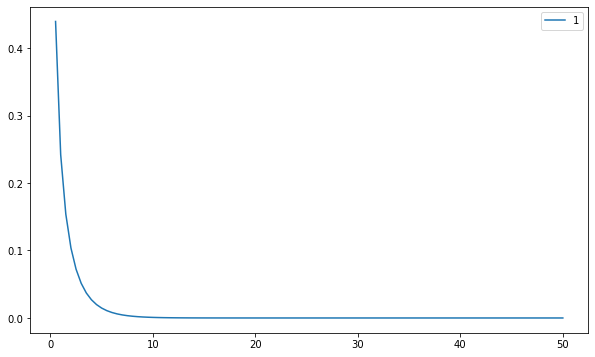
   (1) 자유도 1
   
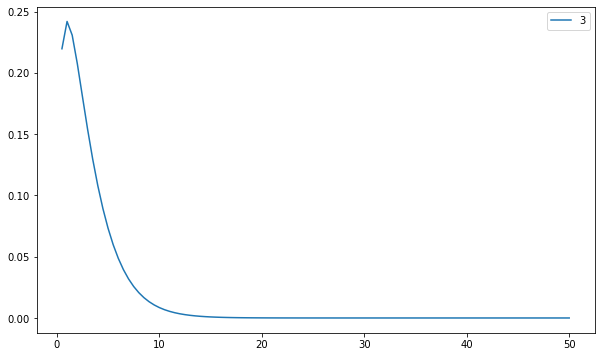
   (2) 자유도 3
   

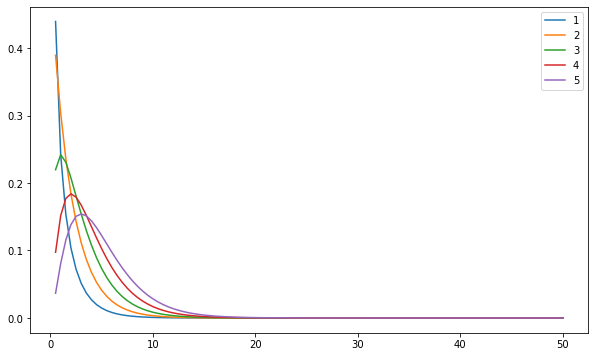
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(0.5, 50,100)
from scipy.stats import chi2
plt.figure(figsize=(10, 6))
for df in [1,2,3,4,5]:
    plt.plot(X, chi2(df).pdf(X), label=df)
    plt.legend()
plt.show()

3. 카이제곱 분포의 쓸모
   (1) 카이제곱 분포는 오차 혹은 편차를 분석할 때 도움을 받을 수 있다.
   
   (2) 중심극한정리에 따르면 샘플수가 무수히 많고 합을 이용해 오차를 정의하면 그 오차의 분포는 정규분포이다.
   Mean-Squared Error : $\frac{1}{n}\sum (X_{pred} - X_{target})$ 정규분포 따른다.
   
   (3) 카이제곱 분포를 통해 오차를 검증하면, 오차가 우연히 발생한 것인지 숨겨진 의미가 있는 오차인 것인지 판별할 수 있다.

카이제곱검정

1. 피어슨 카이제곱 통계량
   $\chi^2=\displaystyle\sum_{i=1}^{} \frac{(O_i-E_i)^2}{E_i}$
   ${(O_i-E_i)^2}$ : 편차의 제곱
   ${E_i}$ : 기댓값으로 정규화 시켜줌

2. 적합도 검정
   (1) 독립변수가 하나이고 이론적으로 기대되는 빈도의 분포와 관찰한 빈도의 분포를 비교
   (2) 독립변수는 범주형 변수이어야 한다.

   	a	b	c	d	e
   관측값	17	16	24	29	14
   예측값	20	20	20	20	20

   
   5가지 맛 사탕이 들어있는 주머니에서 100개의 사탕을 꺼냈을때 관측값 같이 나왔다. 이 주머니에는 사탕 5종류가 같은 비율로 섞여 있다고 할 수 있을까?

• $\chi^2=\frac{(17-20)^2}{20}+\frac{(16-20)^2}{20}+\frac{(24-20)^2}{20}+\frac{(29-20)^2}{20}+\frac{(14-20)^2}{20}=7.9$
• 5개의 카테고리이므로 -> 자유도는 4
  $\chi^2_{(4)}=9.4877$
  
  => 통계량은 상위 5%에 해당하는 $\chi^2$보다 낮으므로 유의미한 차이를 보였다고 하기 어려움

3. 교차분석
   (1) 범주형 변수가 여러개인 경우 적용하는 분석 방법
   (2) 여러 범주형 변수의 범주간 차이가 기댓값에서 유의하게 벗어나는지 알아봄

   	짜장	짬뽕	마라탕	합
   남	21	13	6	40
   여	16	15	14	45
   합	37	28	20	85

   
   남자와 여자간 메뉴 선택 차이가 유의하게 벗어나는가?

• 남자&짜장의 $기대 빈도=\frac{40\times37}{85}=17.41$
  이런식으로 나머지도 다 구해주면
  

• 	짜장	짬뽕	마라탕
  남	17.41	13.18	9.41
  여	19.59	14.82	10.59

  $\chi^2=\frac{(21-17.41)^2}{17.41}+\frac{(13-13.18)^2}{13.18}+\frac{(6-9.41)^2}{9.41}+\frac{(16-19.59)^2}{19.59}+\frac{(15-14.82)^2}{14.82}+\frac{(14-10.59)^2}{10.59}=3.7366$

• 자유도는 (2-1)*(3-1)=2
  $\chi^2_{(2)}=5.9915$
  
  기댓값에서 유의하게 벗어나지 않는다. 따라서 남자와 여자간 메뉴 선택에 유의한 차이가 있다고 할 수 없다.