Classification
📌 3-1. 머신러닝 분류 모델링
✅ Bias-Variance Tradeoff
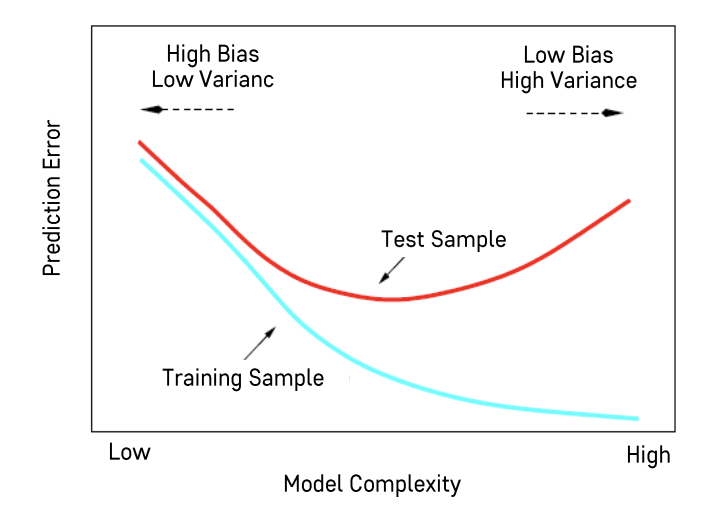
모델의 오차 = bias(모델이 가지고 있는 편향성) + variance(모델의 변동성)
💡 모델의 복잡도를 높이면 bias는 줄어들고, variance는 커진다.
- bias는 줄어든다
👉🏻 모델이 복잡할수록 training data를 잘 설명할 수 있다. (= 완벽하게 학습한다) - variance는 커진다
👉🏻 데이터를 너무 미세하게 학습했기 때문에 데이터의 구성이 조금만 달라져도 변동성이 커진다. (= 오차가 증가한다)
💡 모델의 복잡도를 낮추면 bias는 커지고, variance는 줄어든다.
- 간단한 모델을 만들어 학습하기 때문에 모델의 예측 성능이 낮아지는 대신 데이터 구성에 대한 변동성이 줄어든다.
- bias가 커졌기 때문에 모델의 오차가 증가한다.
💡
- bias와 variance가 적절하게 조정된 최적의 prediction error를 갖는 모델을 선택하는 것이 목표
- prediction error는 모델의 복잡도(model complexity)와 연관되어 있고, 이 복잡도를 결정하는 것이 hyperparameter이다.
📌 3-2. K-Nearest Neighbours (KNN)
💡 두 관측치의 거리가 가까우면 Y(label)도 비슷하다.
- K == 임의의 숫자; 모형의 복잡도를 결정하는 hyperparameter
- K개의 주변 관측치 class에 대한 majority voting
- Distance-based model과 Instance-based model이 있다.
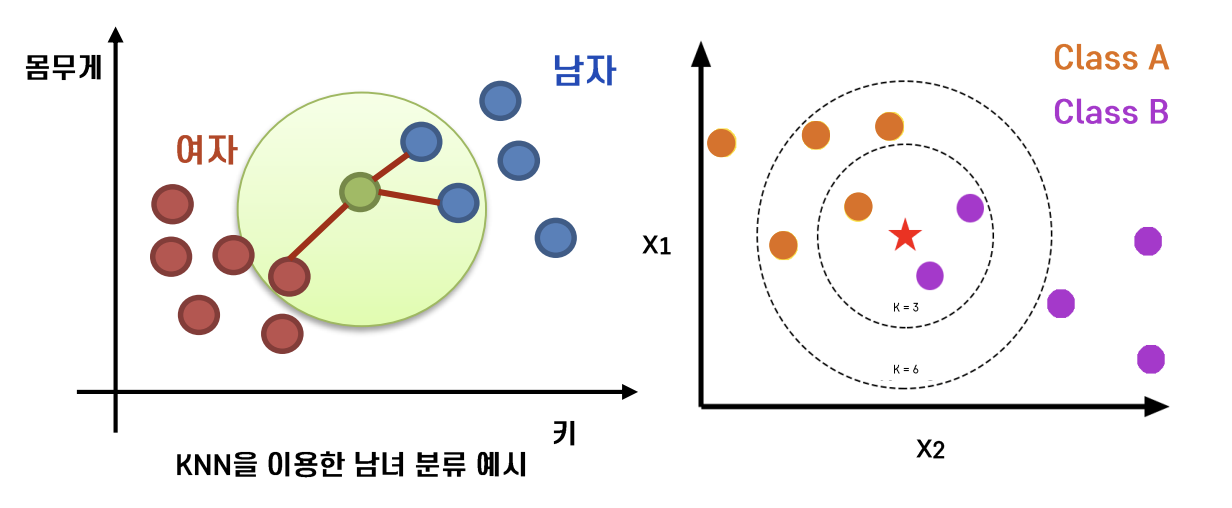
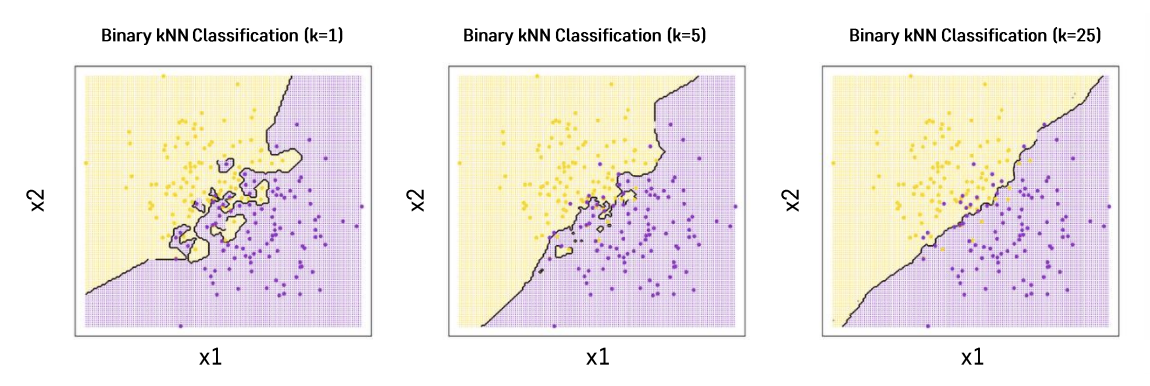
K에 따라 분류 경계선의 형태가 달라지면서 모형의 복잡도와 연관이 된다.
❗️ K에 따라서 분류의 결과가 달라진다.
- K가 클수록 Underfitting / K가 작을수록 Overfitting
- K가 크면 클수록 주위에 더 많은 사례를 보기 때문에 좀 더 단순한 분류 경계선을 그려 모델의 복잡도가 낮다.
- K가 작으면 작을수록 주변의 미세한 패턴을 분류하기 때문에 모델의 복잡도가 높다.
✅ 거리 계산
- KNN은 기본 함수 형태도, 기본 파라미터도 없다.
- 두 관측치 사이의 거리를 측정
- 범주형 변수는 dummy variable로 변환하여 거리 계산
🤔 Note: KNN은 Lazy Learning Algorithm이라고도 불린다.
-
다른 알고리즘들, 예를 들면 Linear Regression, 은 training data를 학습시키면 최종 모델 형태가 결정되고 파라미터 계산을 통해 결과물이 나오는 반면, KNN은 training dat를 활용하지 않고 testing 단계에서 testing data를 기준으로 training data와의 거리를 구한 후 최종 결과물을 내기 때문이다.
-
따라서, KNN을 실시간으로 분석해야하는 빅데이터에 사용하는 것은 어렵지만, 기본적인 형태의 데이터를 실시간으로 활용하지 않는 상황에서는 충분한 효과를 볼 수 있다.
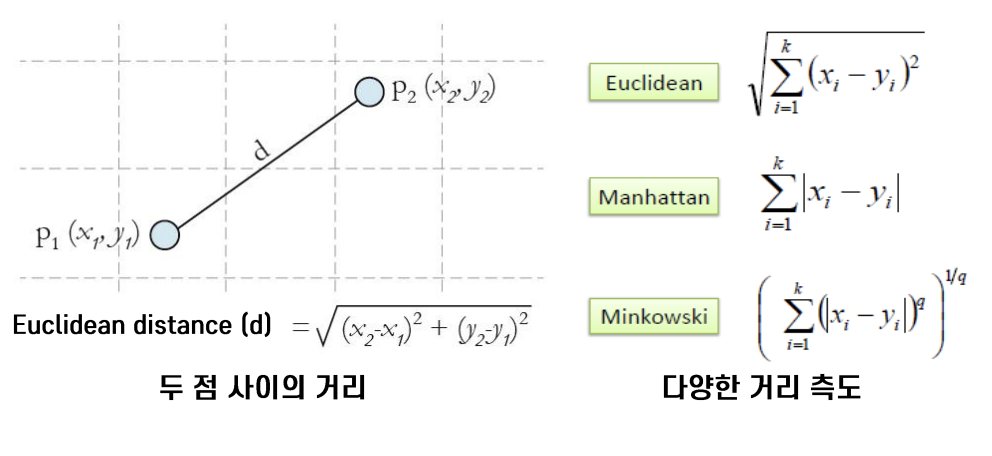
1) Euclidean distance
- 가장 대표적인 거리 측도
- 데이터 공간에서 두 점 사이의 거리를 구하는 공식
2) Manhattan distance
- 각각의 절댓값을 더하는 방식 (x축의 차이 + y축의 차이)
- 측정하는 대상을 완벽하게 독립적으로 생각하고 변수별로 거리를 계산하고자 할 때 사용
3) Dummy variable
- 범주형 변수를 dummy variable로 변환한 후 거리 계산
- 같은 클래스끼리는 거리가 0, 다른 클래스끼리의 거리 값을 측정
📌 3-3. Logistic Regression
Linear Regression의 Classification 버전 (label이 범주형 변수)
- 범주형 변수를 output으로 출력해야하기 때문에 일반 회귀 분석(Linear Regression)과는 다른 방식으로 접근할 필요성이 있다.
🤔 Logistic Regression의 목적?
- 이진형 (0/1)의 형태를 갖는 종속변수(분류문제)에 대해 회귀식의 형태로 모델을 추정
🤔 왜 회귀식으로 표현해야 하는가?
회귀식으로 표현될 경우 변수의 통계적 유의성 분석 및 종속변수에 미치는 영향력 등을 알아볼 수 있다.
참고
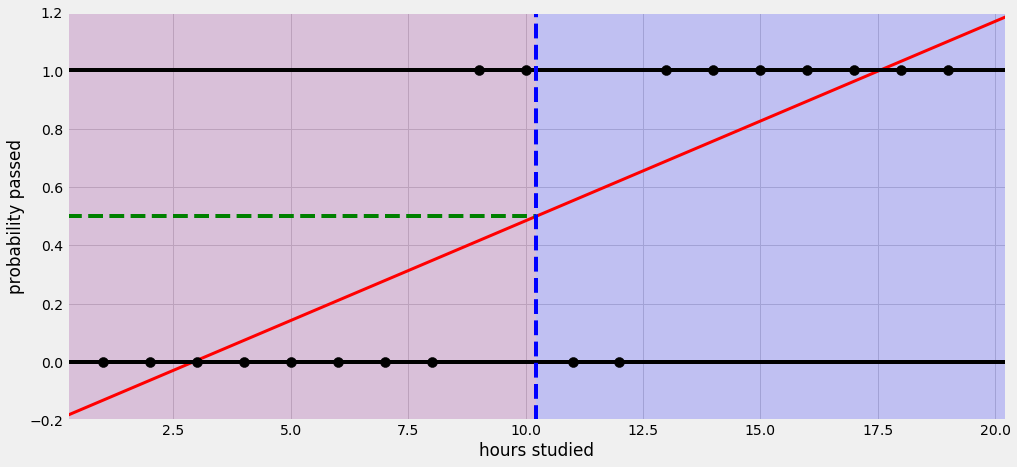
예를 들어 어떤 학생이 공부하는 시간에 따라 시험에 합격할 확률이 달라진다고 해보자. 선형 회귀를 사용하면 아래와 같은 그림으로 나타낼 수 있다.
공부한 시간이 적으면 시험에 통과 못하고, 공부한 시간이 많으면 시험에 통과한다는 식으로 설명할 수 있다. 그런데 이 회귀선을 자세히 살펴보면 확률이 음과 양의 방향으로 무한대까지 뻗어 간다. 말 그대로 ‘선’이라서. 그래서 공부를 2시간도 안 하면 시험에 통과할 확률이 0이 안 된다. 이건 말이 안 된다.
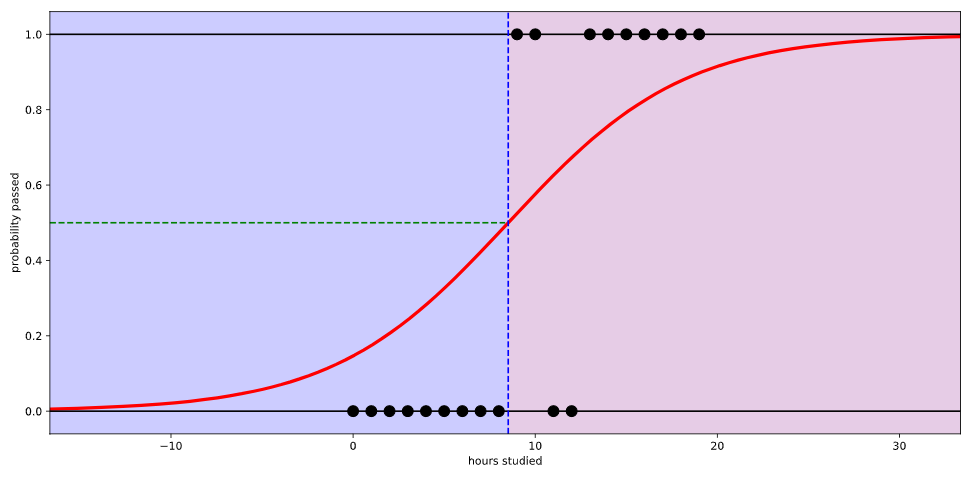
만약 로지스틱 회귀를 사용하면 아래와 같이 나타난다.
시험에 합격할 확률이 0과 1사이의 값으로 그려진다. 이제야 좀 납득이 된다.
로지스틱 회귀에서는 데이터가 특정 범주에 속할 확률을 예측하기 위해 아래와 같은 단계를 거친다.
- 모든 속성(feature)들의 계수(coefficient)와 절편(intercept)을 0으로 초기화한다.
- 각 속성들의 값(value)에 계수(coefficient)를 곱해서 log-odds를 구한다.
- log-odds를 sigmoid 함수에 넣어서 [0,1] 범위의 확률을 구한다.
🤔 Logistic Regression의 특징?
- 이진형 종속변수 Y를 그대로 사용하는 것이 아니라 Y에 대한 logit function을 회귀식에 종속변수로 사용
- logit function은 설명변수의 선형결합으로 표현
- logit function의 값은 종속변수에 대한 성공확률로 역산될 수 있으며 따라서 이는 분류 문제에 적용 가능
1) 모델링
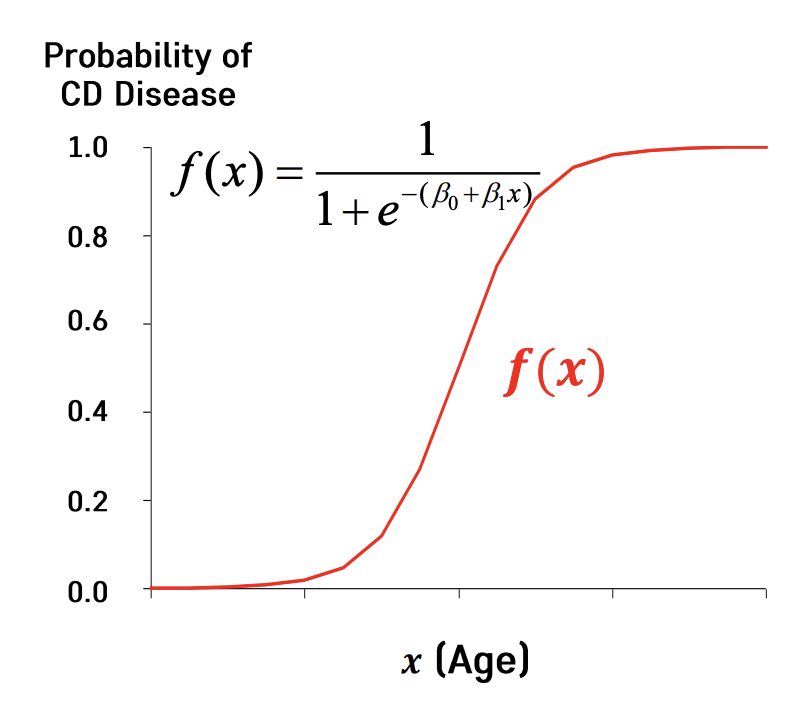
Sigmoid 함수를 이용해서 최종 결과값을 계산
2) Loss (실제값 - 예측값) 정의
💡 분류에는 Cross-entropy라는 loss를 많이 사용
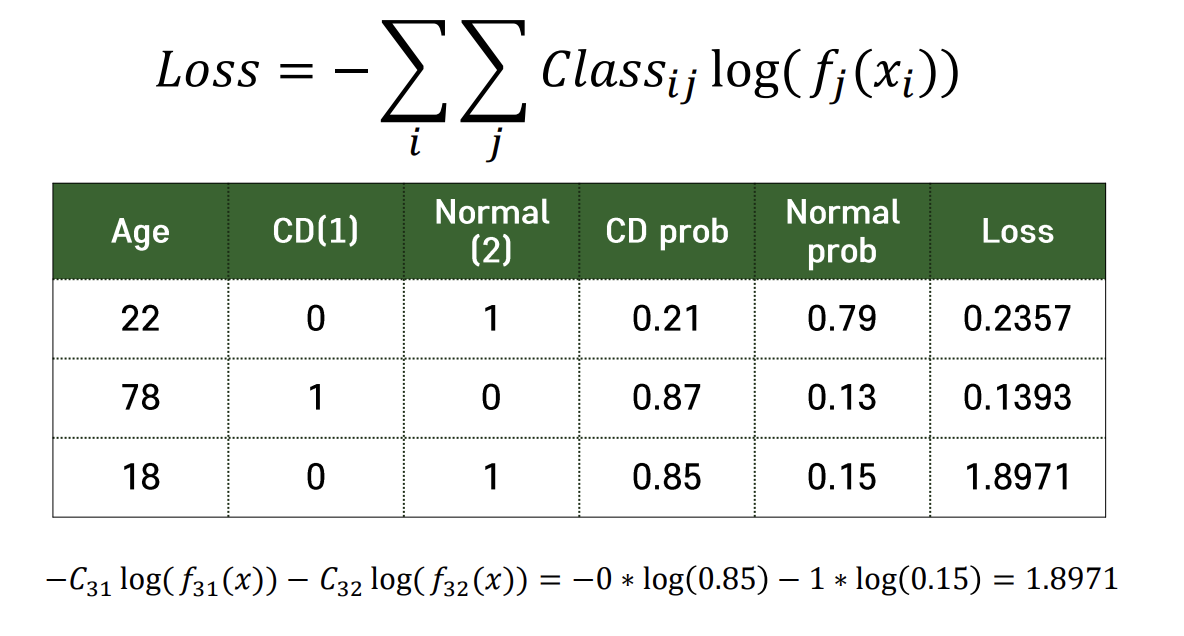
실제 클래스의 분류확률값에 log를 취해서 최종 분류결과 도출
🤔 Cross-entropy loss를 최소화 해주면?
실제 클래스로 분류될 확률이 높여주게된다.
e.g. 위 테이블에서 나이가 18세인 환자는 실제 normal이지만 분류기가 해당 환자가 암일 확률을 0.85로 잘못 분류했다. 실제 클래스로 분류될 확률이 낮으니까 loss값이 굉장히 커지게 된다.