Week_04 주차를 마치며 내가 일주일 동안 공부 해온 내용들을 글로 작성해보며 기록을 남기려고 한다.
week_04 이번 주 백준 문제 풀이 카테고리는 다음과 같이 명시되어 있다.
- DP (Dynamic Programming)
- 그리디 알고리즘
드디어 4주차 자료구조와 알고리즘 마지막 주차이다. (마지막 주차라고 하지만 나는 계속 복습하면서 공부하지 않을까.?) 하지만 계속 유형을 반복해서 접해보고 더 익숙해질 필요가 있는 것 같다. 아직 문제를 풀 때 답을 보고 푸는 경우가 점점 더 많아지는 것 같아서 나 스스로 익숙해지는 과정이고 그 과정이 지나가는 시간이 필요하다고 생각한다. 모든 일엔 과정이 있고 그 과정에서 얼마나 묵묵히 자기 할 일을 했느냐에 있어서 성과가 나오고 결과물이 도출된다. 나도 좋은 성과를 내기 위해선 지치지 않고 더 열심히 노력해야겠다.
- DP (Dynamic Programming)

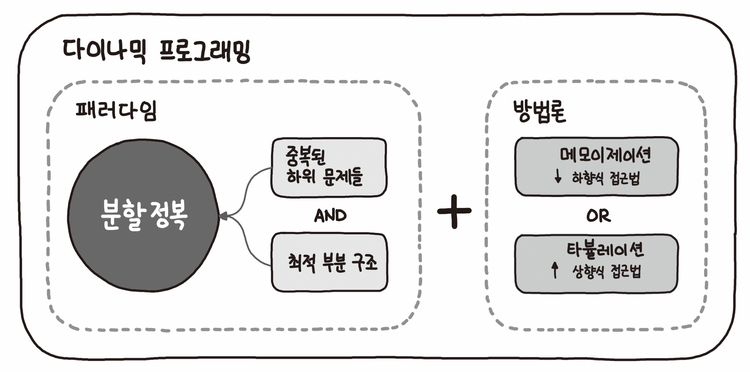
동적 계획법(dynamic programming)이란 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 이것은 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용한다.
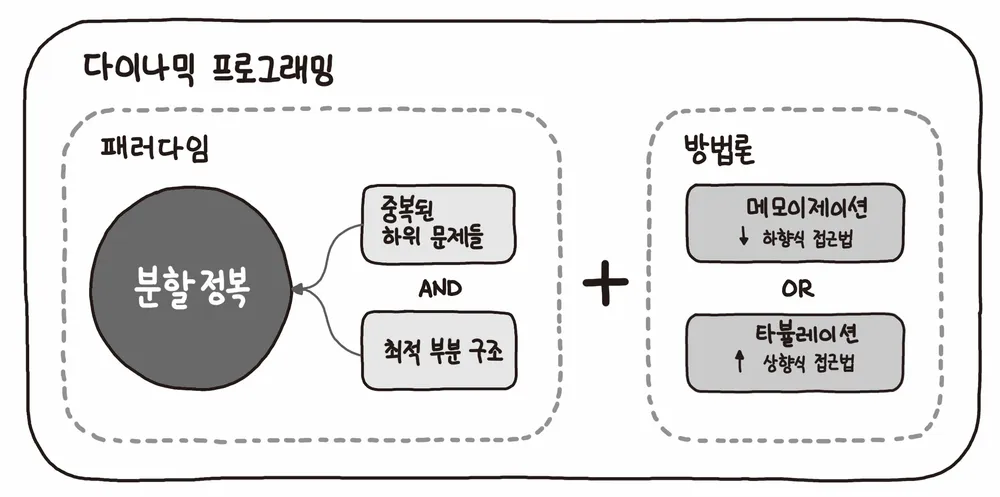
DP의 실행 조건:
-
부분 반복 문제(Overlapping Subproblem)
-
최적 부분 구조(Optimal Substructure)
위 두 가지 속성을 만족 시켜야 한다.
동적 계획법의 개념과 구현에 대해 정확하게 짚고 넘어가기 위해 동적 계획법을 적용시킬 수 있는 예에 대해 알아보자.
f(a,b) = f(a-1,b) + f(a,b-1) (a,b >= 1 )
f(0,0) = 1, 임의의 자연수 n에 대해 f(n,0) = f(0,n) = 1
위와 같이 정의된 함수에서 주어진 임의의 a,b에 대해 f(a,b)의 값을 효율적으로 구하고자 할 때 동적 계획법을 적용시킬 수 있다.
예를 들어 f(2,2)을 계산한다고 해보자. 이 경우 아래 그림과 같은 참조를 거치게 된다.
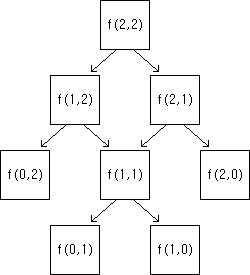
순서대로 계산횟수를 구해보면 f(2,2)를 구하기 위해 총 5번의 연산을 거쳐야한다. 이때 중복되는 부분 문제[3]에 대한 답을 미리 계산해놓고 연산한다고 가정했을 때 계산횟수를 구해보면 f(2,2)를 구하기 위해 4번의 연산을 거쳐야한다. 이 경우 간단한 예라 중복되는 부분 문제가 f(1,1) 하나뿐이기 때문에 큰 속도의 이득을 볼 수 없지만 a, b의 값이 커질수록 속도 면에서 엄청난 이득을 볼 수 있다. 몇 가지 a, b 값에 대해 f(a, b)를 구하기 위한 연산 횟수를 나타낸 아래 표를 참고해보자.

이 정도면 아마 대충 동적 계획법의 효율이 느껴질 것이다. 실제로 a, b가 1 증가할 때마다 연산 횟수는 기하급수적으로 증가하며, 이때 중복되는 부분 문제를 적절히 처리해줌으로써 높은 계산효율을 얻을 수 있는 것이다.
DP 참고:
1:https://velog.io/@gillog/%EB%8F%99%EC%A0%81-%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming
2:https://namu.wiki/w/%EB%8F%99%EC%A0%81%20%EA%B3%84%ED%9A%8D%EB%B2%95
- DP (Dynamic Programming)
백준 2748 (피보나치 수 2):
문제 출처: https://www.acmicpc.net/problem/2748
피보나치 수 2문제 같은 경우 동적 계획법을 사용해서 풀어보았는데 확실히 재귀만 사용했을 때와 DP를 같이 사용했을 때 속도 차이가 어마어마하게 났다. 그래서 둘의 시간복잡도를 잠깐 얘기해 보자면 해당 문제를 그냥 재귀만 사용해서 풀 때 O(2^N), 이 나오는데 DP를 같이 사용한다면 O(N), 이 나오면서 속도도 빠르게 메모리도 훨씬 적게 차지하게 되어 유용한 방법이라는 걸 알게 됐다.
내 정답 코드)
# 하향식 풀이법 (Top-Down)
import sys
input = sys.stdin.readline
dp = [-1] * 100
dp[0] = 0
dp[1] = 1
def fibo(n):
if dp[n] == -1:
dp[n] = fibo(n-1) + fibo(n-2)
return dp[n]
n = int(input())
print(fibo(n))백준 1904 (01타일):
문제 출처: https://www.acmicpc.net/problem/1904
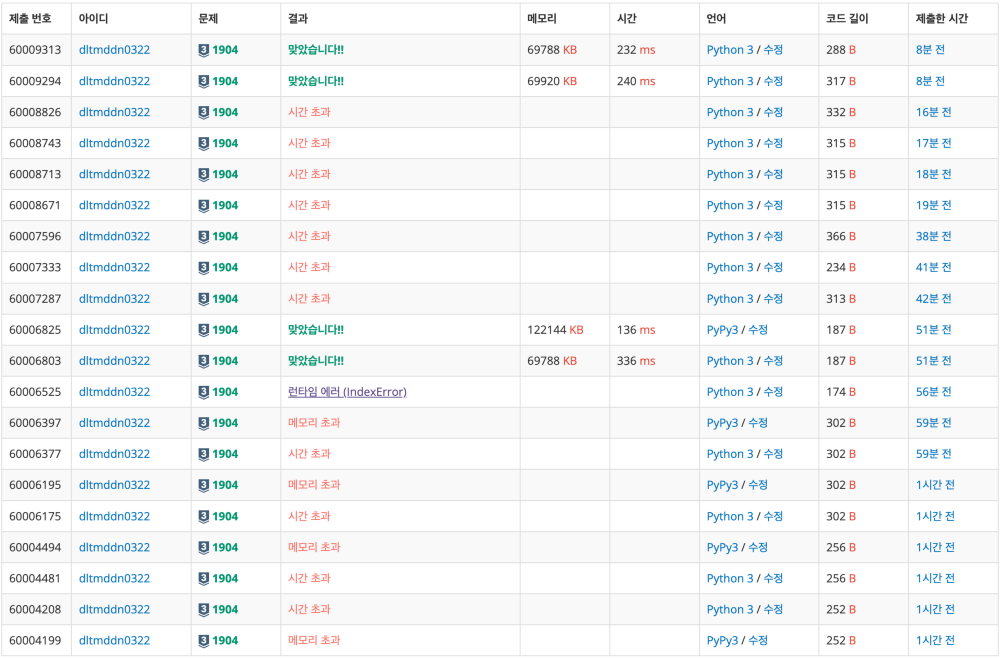
01타일 문제 같은 경우 처음에 상향식으로 풀어보고 하향식으로도 풀어보려고 했지만 알고보니 파이썬 언어 특성상 받아 들이기 힘든 부분들이 존재 했다,, 재귀로 풀어보려고 해도 계속 시간 초과 나 메모리 초과가 나와서 (내 접근 방식이 맞나 라고 의심이 들기 시작했고 구글링을 해봐도 대부분 반복문으로 풀고 재귀로 푼 사람이 없었다..) 쉽지 않은 문제 였지만 그래도 나중에 다른 문제들을 마주할때 조금은 변별력이 생긴 것 같아서 나쁘지 않은 시도 였던것 같다.
내 정답 코드)
# 상향식 풀이법 (Bottom-Up)
import sys
input = sys.stdin.readline
n = int(input())
dp = [-1] * 1000001
dp[1] = 1
dp[2] = 2
def tile(n):
if n == 1:
return 1
elif n == 2:
return 2
else:
for i in range(3, n+1):
dp[i] = (dp[i-1] + dp[i-2]) % 15746
tile(n)
print(dp[n])
# 하향식 풀이법 (파이썬 에선 안됌 X, but C++ 가능)백준 9084 (동전):
문제 출처: https://www.acmicpc.net/problem/9084
동전 문제 같은 경우 상향식으로 처음에 풀어보고 하향식으로 바꿔봤는데 중간에 recursion limit exceed 떠서 sys.recursionlimit(10**6)을 설정해주니까 정답 처리가 됐다. 파이선 내부에서 지정한 recursion limit 때문에 해결이 안 됐는데 Chat-GPT에 물어보니 재귀호출 제한을 풀어주면 해결된다 해서 풀어주었더니 해결됐다.
내 정답 코드)
# 상향식 풀이법 (Bottom-Up)
import sys
input = sys.stdin.readline
T = int(input()) # 테스트 케이스 개수
for _ in range(T):
N = int(input()) # 동전의 종류 수
coins = list(map(int, input().split())) # 동전 가치
M = int(input()) # 만들어야 하는 금액
dp = [0] * (M+1)
dp[0] = 1 # 0원을 만들 수 있는 경우의 수는 1개 (아무 동전도 사용하지 않는 경우)
for coin in coins:
for i in range(coin, M+1):
dp[i] += dp[i-coin]
print(dp[M])
# 하향식 풀이법 (Top-Down)
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def count_ways(coins, target, memo):
if target == 0:
return 1
if target < 0:
return 0
if len(coins) == 0:
return 0
key = (len(coins), target)
if key in memo:
return memo[key]
memo[key] = count_ways(coins[:-1], target, memo) + count_ways(coins, target-coins[-1], memo)
return memo[key]
T = int(input()) # 테스트 케이스 개수
for _ in range(T):
N = int(input()) # 동전의 종류 수
coins = list(map(int, input().split())) # 동전 가치
M = int(input()) # 만들어야 하는 금액
memo = {}
result = count_ways(coins, M, memo)
print(result)
백준 9251 (LCS):
문제 출처: https://www.acmicpc.net/problem/9251
LCS 문제 같은 경우 Longest Common Subsequence, 최장 공통부분 수열이라 불리는데 말 그대로 주어진 수열 중 각 수열의 부분 수열을 비교 해봤을 때 공통으로 들어가는 부분 수열 중 가장 긴 부분 수열을 구하는 문제이다. 말로 설명해서 이해하기엔 어려운 부분이 있으니 예시를 들어보면:
예를 들어,
1: ACAYKP
2: CAPCAK
두 수열이 주어졌을 때 두 수열의 부분 수열은 여러 가지가 나오지만 그중 가장 긴 부분 수열(LCS)은 ACAK 이다.
해당 문제 또한 상향식, 하향식 풀이를 둘 다 해보았다. 두 가지 풀이를 해보니 느끼는 점은 확실히 DP를 사용하는 것이 조금씩 눈에 보이기 시작했다. 그리고 재귀함수를 이용하면서 정말 비효율적이라는 생각이 들었지만, (재귀로 구현 하면 가독성이 좋긴 하다,,) DP를 적용함으로써 메모리 와 시간을 조절해서 해결할 수 있다는 점이 DP를 쓰는 가장 큰 이유이지 않을까 생각이 든다. (왜냐하면 문제 마다 메모리를 적게 주거나 시간을 적게 주는경우도 있기 떄문이지 않을까..?)
내 정답 코드)
# 상향식 풀이법 (Bottom-Up)
import sys
input = sys.stdin.readline
x = input().strip()
y = input().strip()
def LCS(x, y):
m = len(x)
n = len(y)
# dp 배열 초기화
dp = [[0] * (n+1) for _ in range(m+1)]
# LCS 계산
for i in range(1, m+1):
for j in range(1, n+1):
if x[i-1] == y[j-1]: # 문자가 같은 경우
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[m][n]
print(LCS(x, y))
# [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 1, 1, 1, 1],
# [0, 1, 1, 1, 2, 2, 2],
# [0, 1, 2, 2, 2, 3, 3],
# [0, 1, 2, 2, 2, 3, 3],
# [0, 1, 2, 2, 2, 3, 4],
# [0, 1, 2, 3, 3, 3, 4]]
# 하향식 풀이법 (Top-Down)
import sys
sys.setrecursionlimit(10**4)
input = sys.stdin.readline
x = input().strip()
y = input().strip()
# 재귀함수로 구현한 LCS 함수
def LCS(x, y, m, n, dp):
if m == 0 or n == 0: # 더 이상 비교항 문자열이 없는 경우
return 0
if dp[m][n] != -1: # 이미 계산된 경우
return dp[m][n]
if x[m-1] == y[n-1]: # 문자가 같은 경우
dp[m][n] = LCS(x, y, m-1, n-1, dp) + 1
else:
dp[m][n] = max(LCS(x, y, m-1, n, dp), LCS(x, y, m, n-1, dp))
return dp[m][n]
# LCS 함수 호출
dp = [[-1] * (len(y)+1) for _ in range(len(x)+1)]
print(LCS(x, y, len(x), len(y), dp))백준 12865(평범한 배낭):
문제 출처: https://www.acmicpc.net/problem/12865

정답 순서:
1: 첫번째 정답이 상향식 풀이(반복문 풀이)
2: 두번째 정답이 하향식 풀이(재귀함수 풀이)
평범한 배낭 문제 같은 경우 상향식, 하향식 풀이를 해보면서 확실히 재귀함수를 사용해서 풀이하면 가독성이 반복문을 사용해서 풀이했을 때 비해 좋은 편이고 코드 수정 하기도 편한 부분이 있다. 하지만, 메모리나 시간 방면에서는 확실히 반복문 풀이가 더 효율적이다, 그래도 재귀를 쓰는 이유는 (with DP) 아무래도 문제마다 주어진 시간과 메모리양이 다르므로 문제마다 메모리를 줄이거나 시간을 줄여서 풀어야 할 때 유동적으로 쓰기 위해서 쓰는 이유인 것 같다. 여러 방식으로 접근해보니 확실히 이런 차이점을 깨닫는 것 같다.
내 정답 코드)
# 상향식 풀이법 (Bottom-Up)
import sys
input = sys.stdin.readline
n, k = map(int, input().split()) # 물건의 개수와 배낭의 최대 무게 입력 받기
w, v = [], [] # 물건의 무게와 가치를 저장할 리스트 생성
for i in range(n):
weight, value = map(int, input().split())
w.append(weight)
v.append(value)
dp = [[0] * (k+1) for _ in range(n+1)] # dp 테이블 생성
for i in range(1, n+1):
for j in range(1, k+1):
if j < w[i-1]: # i번째 물건을 선택할 수 없는 경우
dp[i][j] = dp[i-1][j]
else: # i번쨰 물건을 선택할 수 있는 경우
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i-1]] + v[i-1])
print(dp[n][k]) # 배낭에 담을 수 있는 최대 가치 출력
# 하향식 풀이법 (Top-Down)
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
w, v = [], []
for i in range(n):
weight, value = map(int, input().split())
w.append(weight)
v.append(value)
dp = [[-1] * (k+1) for _ in range(n+1)]
def Bag(i, j):
if dp[i][j] != -1:
return dp[i][j]
if i == 0 or j == 0:
dp[i][j] = 0
return dp[i][j]
if j < w[i-1]:
dp[i][j] = Bag(i-1, j)
return dp[i][j]
dp[i][j] = max(Bag(i-1, j), Bag(i-1, j-w[i-1]) + v[i-1])
return dp[i][j]
print(Bag(n, k))백준 11049 (행렬 곱셈 순서):
문제 출처: https://www.acmicpc.net/problem/11049
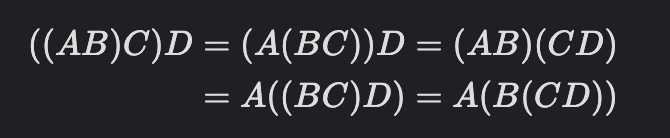
행렬 곱셈 순서 문제 같은 경우 행렬곱을 알고 있어야 연쇄 행렬 곱셈도 할수 있다.
행렬곱의 전제 조건 같은 경우 다음과 같다:
- 처음에 A = M N 크기인 행렬, B = N K 크기인 행렬이 주어진다.
- A 행렬의 열(N) 과 B행렬의 행(N) 이 같으면 곱셈이 성사 되므로 이때, AB 행렬의 크기는 M * K 이다.
내 정답 코드)
# pypy3 만 통과 상향식 풀이법 (Bottom-Up)
import sys
sys.setrecursionlimit(10**4)
input = sys.stdin.readline
n = int(input()) # 행렬의 개수를 입력받음
matrix = [] # 행렬의 크기를 저장할 리스트
for _ in range(n):
r, c = map(int, input().split()) # 행렬의 크기를 입력받음
matrix.append((r, c)) # 입력받은 행렬의 크기를 리스트에 추가함
dp = [[0] * n for _ in range(n)] # dp 테이블 초기화
for i in range(1, n): # 행렬 곱셉의 길이를 1부터 n-1까지 반복
for j in range(0, n-i): # 시작하는 행렬의 인덱스를 0부터 n-i-1까지 반복
dp[j][j+i] = sys.maxsize # dp[j][j+i]를 최댓값으로 초기화
for k in range(j, j+i): # k를 j부터 j+i-1까지 반복
# dp[j][k]와 dp[k+1][j+i]를 더한 값과
# 행렬 j부터 j+i까지의 곱셈을 했을 때의 곱셈 연산 횟수를 곱한 값을
# dp[j][j+i]에 저장함
dp[j][j+i] = min(dp[j][j+i], dp[j][k] + dp[k+1][j+i] + matrix[j][0]*matrix[k][1]*matrix[j+i][1])
print(dp[0][n-1]) # 행렬 0부터 n-1까지의 곱셈을 하는데 필요한 최소 곱셈 연산 횟수를 출력함
# 하향식 풀이법 (Top-Down)
import sys
sys.setrecursionlimit(10**4)
input = sys.stdin.readline
def matrix_chain_multiplication(matrix, dp, i, j):
if dp[i][j] < sys.maxsize:
return dp[i][j]
if i == j:
dp[i][j] = 0
return 0
for k in range(i, j):
dp[i][j] = min(dp[i][j], matrix_chain_multiplication(matrix, dp, i, k) + matrix_chain_multiplication(matrix, dp, k+1, j) + matrix[i][0]*matrix[k][1]*matrix[j][1])
return dp[i][j]
n = int(input())
matrix = []
for _ in range(n):
r, c = map(int, input().split())
matrix.append((r, c))
dp = [[sys.maxsize] * n for _ in range(n)]
matrix_chain_multiplication(matrix, dp, 0, n-1)
print(dp[0][n-1])백준 11053 (가장 긴 증가하는 부분 수열):
문제 출처: https://www.acmicpc.net/problem/11053
가장 긴 증가하는 부분 수열 문제 같은 경우 dp 를 이용해서 풀면 생각보다 간단한 문제라고 생각이 든다. 이번에도 마찬가지로 상향식 과 하향식 2가지 방식 모두 구현 해보았다. 상향식 같은 경우 코드도 꽤 간결하지만 실제로 코드를 하나하나 뜯어 보면 생각 보다 복잡하다. 하지만 하향식으로 보면 예외처리를 하는 부분은 훨씬 직관적이고 코드가 전체적으로 가독성이 좋고 수정하기에도 편해서 나중에 사용하기 쉽게 좀더 익숙해지려고 재귀함수를 계속 연습하는 중이다,, (재귀함수가 아직 많이 익숙치 않아서 코드 짜기 쉽지가 않다...)
for i in range(index-1, -1, -1):
if a[i] < a[index]:
dp[index] = max(dp[index], lis(i) + 1)하향식으로 풀때 중요한 포인트는 바로 이 부분인것 같다. a 수열 안에 있는 숫자들을 인덱스로 접근해서 현재 숫자와 바로 전 위치에 있던 숫자들을 비교해 가면서 최대 값들을 현재 위치에 넣어주는게 바로 규칙성이고 이런 규칙성이 재귀를 사용할때 가장 중요한 포인트 인것 같다. (이런 부분들을 코드를 작성할때도 바로 생각이 날 정도로 익숙해지려면 한참 멀었지만 목표는 익숙하게 사용할 정도가 되는것이다.)
내 정답 코드)
# 상향식 풀이법 (Bottom-Up)
import sys
input = sys.stdin.readline
n = int(input()) # 6
a = list(map(int, input().split())) # [10, 20, 10, 30, 20, 50]
dp = [1] * n # [1, 1, 1, 1, 1, 1] => [1, 2, 1, 3, 2, 4]
for i in range(n):
for j in range(i):
if a[j] < a[i]: # i=1, j=0
dp[i] = max(dp[i], dp[j] + 1)
print(max(dp))
# 하향식 풀이법 (Top-Down)
import sys
input = sys.stdin.readline
n = int(input()) # 6
a = list(map(int, input().split())) # [10, 20, 10, 30, 20, 50]
dp = [-1] * n # [-1, -1, -1, -1, -1, -1] => [1, 2, 1, 3, 2, 4]
def lis(index):
if dp[index] != -1:
return dp[index]
dp[index] = 1
for i in range(index-1, -1, -1):
if a[i] < a[index]:
dp[index] = max(dp[index], lis(i) + 1)
return dp[index]
ans = 0
for i in range(n):
ans = max(ans, lis(i)) # (4)
print(ans)백준 2098 (외판원 순회):
문제 출처: https://www.acmicpc.net/problem/2098
외판원 순회 문제 같은 경우 dp를 이용해서 재귀적으로 코드를 짜보았다. (역시 Chat-GPT) 내가 스스로 생각해서 짜기엔 너무 역부족 이였고 예전에 푼 외판원 순회 2에서는 완전 탐색으로 풀었지만 여기선 dp를 사용안하면 시간초과가 뜬다. 그러므로 Chat-GPT를 이용해서 문제를 먼저 파악해보고 아이디어를 구상했지만 비트마스킹이라는 자료구조를 또 알아야 한다는 사실을 나중에 깨닫고 비트 연산자를 잘 모르면 풀기 힘들것 같다는 생각이 들었다. 그래서 비트 연산자에 대해 간략히 개념 파악만 하고 문제에 접근 해봤지만 실질적으로 코드안에 사용하는 부분은 또 다른 영역이라는걸 깨닫고 구글링을 통해 답을 보면서 코드를 이해 하고 다시 짜보았다. 이 문제는 나중에 다시 한번더 풀어봐야 할것 같다,,
짱..!
내 정답 코드)
# 하향식 풀이법(Top-Down)
import sys
INF = sys.maxsize # 무한대 값으로 초기화
def tsp(curr, visited):
# 모든 도시를 방문한 경우, 현재 도시에서 출발 도시로 돌아가는 비용을 반환
if visited == (1 << N) - 1: # 1 == 15 # 3 == 15
return graph[curr][0] if graph[curr][0] > 0 else INF
# 이미 계산한 값이 있는 경우, 바로 반환
if dp[curr][visited] != -1:
return dp[curr][visited]
# 최소 비용으로 도시를 방문하는 경로를 찾음
result = INF
for i in range(1, N):
# 이미 방문한 도시는 건너뛰기
if visited & (1 << i):
continue
# 현재 도시에서 다음 도시로 이동하는 비용
cost = graph[curr][i]
if cost == 0:
continue
# 다음 도시를 방문한 경우의 비용 계산
next_visited = visited | (1 << i)
next_cost = cost + tsp(i, next_visited)
# 최소 비용 갱신
result = min(result, next_cost)
# 결과 저장 후 반환
dp[curr][visited] = result
return result
N = int(input()) # 도시의 개수
graph = [list(map(int, input().split())) for _ in range(N)] # 비용 그래프
# 메모이제이션을 위한 DP 테이블 초기화
dp = [[-1] * (1 << N) for _ in range(N)]
# 출발 도시는 0번 도시로 고정
start = 0
visited = 1 << start
# 최소 비용으로 모든 도시를 방문하는 경로를 찾음
answer = tsp(start, visited)
print(answer)백준 2253 (점프):
문제 출처: https://www.acmicpc.net/problem/2253
점프 문제 같은 경우 처음엔 상향식 으로 풀어보고 그 이후에 하향식으로 바꿔보는 형식으로 두 방식 모두 접근해서 풀어보았다. 처음엔 상향식으로 접근 할때 dp를 이용하고 반복문으로 구현해봤는데 처음엔 점화식을 이용해서 푼다 라는 생각 조차 하지 못했어서 (Chat GPT가 알려줌) 쉽지 않았는데 코드를 짜기전 아이디어를 구상하다보니 문득 돌의 개수가 주어지고 점프해서 다음 돌로 가는 속력이 곧 점프 횟수가 될꺼라는 생각이 떠오르는 순간 돌의 개수 가 늘어나는 만큼 점프할수 있는 칸수가 증가 할거 같아서 indexError 가 나올것 같았다. 그래서 아이디어는 이렇지만 코드로 직접 어떻게 구현해낼까 라는 생각이 들때 구글링을 해보고 점화식을 참고로 보니 문제을 어떻게 해결해야 할지 감이 서서히 오기 시작했다.
해당 문제를 풀때 포인트는 다음과 같다:
- 필요 요소
- 못 건너는 돌 위치를 저장할 리스트
- 현재 돌까지 점프해서 올 수 있는 이전 돌의 점프 횟수를 기록할 2차원 dp배열
dp배열에 대해 설명을 추가하자면
dp[i][v]라 하면 i번째 돌(y축)로 v의 속도(x축)로 왔을 때의 최소값이라 할 수 있다.
dp[i][v]로 올 수 있는 경우는 dp[i-v][v-1], dp[i-v][v], dp[i-v][v] 이렇게 있는 셈이다.

int((2*N)^0.5)의 의미
-> 불필요한 연산을 막기 위한 연산
등차수열의 합 공식 = k(2a+(k-1)d) / 2
(이 문제에서 a(첫 번째 수) =1, d(공차) =1 )
따라서 마지막에 있는 돌까지 가장 빠르게 갈 수 있는 돌들의 수의 합 N
= k(k+1)/2
k = (2N-k)^0.5 <= 2N^0.5
내 정답 코드)
# 상향식 풀이법(Bottom-Up)
import sys
input = sys.stdin.readline
def sol():
n, m = map(int, input().split())
dp = [[float('inf')] * (int((2*n)**0.5)+2) for _ in range(n+1)]
dp[1][0] = 0
stn = []
for _ in range(m):
stn.append(int(input()))
for i in range(2, n+1):
if i in stn:
continue
for v in range(1, int((2*i)**0.5) + 1):
dp[i][v] = min(dp[i-v][v-1], dp[i-v][v], dp[i-v][v+1]) + 1
result = min(dp[n])
if result == float('inf'):
print(-1)
else:
print(result)
sol()
# 하향식 풀이법(Top-Down)
import sys
inf = 2000000000
n, m = map(int, input().split())
cache = [[-1] * 200 for _ in range(10000)]
chk = [False] * 10000
for i in range(m):
stone = int(input())
chk[stone - 1] = True
def dp(now, x):
if now >= n - 1:
return 0 if now == n - 1 else inf
if chk[now]:
return inf
ret = cache[now][x]
if ret != -1:
return ret
ret = dp(now + x + 1, x + 1) + 1
if now != 0:
ret = min(ret, 1 + dp(now + x, x))
if x >= 2:
ret = min(ret, 1 + dp(now + x - 1, x - 1))
cache[now][x] = ret
return ret
result = dp(0, 0)
if result >= inf:
result = -1
print(result)- 그리디 알고리즘
그리디 알고리즘(Greedy Algorithm)은 최적해를 구하는 문제에 적용되는 알고리즘 중 하나로, 각 단계에서 가장 최적의 선택을 하는 방식으로 동작한다. 즉, 주어진 문제에 대해 선택 가능한 여러 가지 선택지 중에서 가장 최적의 선택을 하며 이를 반복적으로 수행하여 최종적인 해답을 찾아낸다. 이 때 각 단계에서의 선택은 지역적으로는 최적의 선택일 수 있으나 전체적으로는 최적의 선택이 아닐 수 있다.
그리디 알고리즘은 일반적으로 다음과 같은 특징을 가집니다.
- 각 단계에서 가장 최적의 선택을 하는 방식으로 동작합니다.
- 지역적으로는 최적의 선택이지만, 전체적으로는 최적의 선택이 아닐 수 있습니다.
- 구현이 간단하며, 실행 속도가 빠릅니다.
그리디 알고리즘의 간단한 개념: https://namu.wiki/w/%EA%B7%B8%EB%A6%AC%EB%94%94%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
- 그리디 알고리즘
백준 11047 (동전 0):
문제 출처: https://www.acmicpc.net/problem/11047
동전 0 문제 같은 경우 동전 가치의 합을 만드는데 필요한 동전 개수의 최솟값을 구하는 문제이다. 이 문제 같은 경우 그리디 알고리즘을 이용해서 풀수 있는데 그리디 알고리즘이라 하면 현 상태에서 가장 최적의 방법을 찾아서 적용 시킨다. 그러므로 이 문제를 풀때에는 가장 큰 동전 수부터 쪼개가면서 동전의 가치의 합에서 해당 동전의 가치를 나누고 그 동전의 개수를 count 시켜 준다. 그리고 가치의 합에서 동전의 가치를 나눈 나머지 를 다시 k에 저장하고 k = 0 이 될때 까지 반복 한후 0이 되면 break 해서 count 값 즉 동전 가치의 합을 만들때 필요한 동전 개수의 최솟값을 프린트 출력 해준다.
내 정답 코드)
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
coins = []
for i in range(n):
coins.append(int(input()))
count = 0 # 동전 개수의 최솟값 초기화
for i in reversed(range(n)): # 동전의 가치가 큰것부터 시작
if k == 0: # 동전 가치의 합이 0이 될때 break
break
if coins[i] <= k: # 해당 동전의 가치가 동전 가치의 합보다 작을때
count += k // coins[i] # count에 동전 가치의 합을 해당 동전의 가치로 나눈 몫을 저장한다
k %= coins[i] # k에 동전 가치의 합을 해당 동전의 가치로 나눈 나머지로 다시 저장한다.
print(count) # 동전 개수의 최솟값을 출력백준 1541 (잃어버린 괄호):
문제 출처: https://www.acmicpc.net/problem/1541
잃어버린 괄호 문제 같은 경우 split() 함수를 잘 이용하면 간단히 풀수 있는 문제이다.
split('기준') 이면 기준을 중심으로 문자열을 나눈다는 의미 이다. 이렇게 실제 코드 상에 적용해보면 연산자를 기준으로 split() 함수를 쓰면 연산자와 숫자를 분리 할수 있고 분리한 숫자를 정수화 시켜서 입력값으로 받은 수식으로 사칙연산이 가능해진다. 그리고 이중 가장 최솟값을 구하는 것이기 때문에 여는 괄호를 항상 '-' 기호 뒤쪽에 붙히는게 연산 했을때 최솟값이 나온다. 이런 아이디어 로직을 기반으로 코드를 짜면 생각보다 문제는 간단히 해결할수 있다.
내 정답 코드)
import sys
input = sys.stdin.readline
formula = input().split('-') # 입력 받는 수식 에서 '-' 기호 기준 으로 나눔
ans = 0 # 정답값 초기화
for i in formula[0].split('+'): # 수식의 0번째 인덱스에 있는 문자열을 '+' 기호 기준으로 나눔
ans += int(i) # ans에 수식의 0번째 인덱스에 있는 i를 정수화 시킨후 더한다.
for i in formula[1:]: # 수식의 1번째 인덱스 부터 시작하는 문자열
for j in i.split('+'): # 수식의 1번째 인덱스의 i 문자열을 '+' 기호 기준으로 나눔
ans -= int(j) # ans에 수식의 1번째 인덱스의 i 문자열을 '+' 기호 기준으로 나눈 문자열 j를 정수화 시킨후 뺀다.
print(ans) # 정답값 출력백준 1931 (회의실 배정):
문제 출처: https://www.acmicpc.net/problem/1931
회의실 배정 문제 같은 경우 기본적인 정렬문제 중 하나인데 포인트는 각 회의의 시작시간과 종료시간이 주어졌을때 둘중 어느 시간을 기준으로 잡고 정렬 할지가 관건인 문제다. 나 같은 경우 각 회의의 종료 시간을 기준으로 정렬 하였다. 그리고 다음 회의 시작시간이 현재 회의종료시간 이후면 회의실을 배정 해서 사용할수 있기 때문에 cnt += 1 해준다. 그리고 다음회의 종료시간을 현재회의 종료 시간으로 업데이트 해주면 끝이다. 조금만 생각해보면 간단하게 풀수 있는 문제들이여서 좋은것 같다. (그리디 알고리즘 생각 보다 괜찮은데..?)
내 정답 코드)
import sys
input = sys.stdin.readline
n = int(input()) # 회의의 수
times = [list(map(int, (input().split()))) for i in range(n)] # 회의 시간
times.sort(key = lambda x: (x[1], x[0])) # 각 회의 종료 시간을 기준으로 정렬
cnt = 1 # 회의의 개수 1로 초기화
for i in range(1, n): # (1부터 n만큼)
if times[0][1] <= times[i][0]: # 다음회의 시작시간이 현재회의 종료시간이 이후이면
cnt += 1
times[0][1] = times[i][1] # 다음회의 종료시간을 현재회의 종료시간으로 업데이트 해준다.
print(cnt) # 회의의 개수 출력백준 1946 (신입 사원):
문제 출처: https://www.acmicpc.net/problem/1946
신입 사원 문제 같은 경우도 기본적인 정렬 문제 중 하나인데 여기서도 포인트는 서류 심사 성적을 기준으로 오름차순 정렬을 한다 그리고 순위를 interview 라는 변수에 저장해서 면접 심사 성적 즉 순위를 비교해서 면접 심사 성적이 더 높은 면접자가 있으면 cnt += 1 해주고 그 성적을 업데이트 해주면 끝난다.
내 정답 코드)
import sys
input = sys.stdin.readline
T = int(input())
for i in range(T):
n = int(input()) # 지원자 수
freshmen = [] # 신입사원 지원자 성적 및 순위 정보 리스트
for j in range(n):
credit, rank = map(int, input().split()) # 성적, 순위
freshmen.append((credit, rank))
freshmen.sort() #서류 심사 성적을 기준으로 오름차순 정렬
cnt = 1 # 선발할수 있는 신입사원 수
interview = freshmen[0][1] # 순위
for k in range(1, n):
if freshmen[k][1] < interview: # 면접 심사 성적이 더 높은 사원이 있으면
cnt += 1
interview = freshmen[k][1] # 면접 심사 성적을 업데이트
print(cnt)