Week_03 주차를 마치며 내가 일주일 동안 공부 해온 내용들을 글로 작성해보며 기록을 남기려고 한다.
week_03 이번 주 백준 문제 풀이 카테고리는 다음과 같이 명시되어 있다.
- 그래프 탐색 기본
- DFS
- BFS
- 위상 정렬
3주차에 접어 들면서 자료구조 와 알고리즘 개념 공부 와 문제 풀이를 같이 하니 문제 난이도가 높아지면서 지나온 주차 보다 확실히 속도도 느려지고 많이 어렵다,, 하지만 계속 유형을 반복해서 접해보고 문제를 이해 하고 다음에 비슷한 문제를 접했을때 접근 방식을 나 스스로 떠올리고 구상할수 있게끔 코드를 짜보는것이 내 목표이다. 현재에 주어진 것에 집중하고 몰입 하자.
- 그래프 탐색 기본

그래프 탐색 기본 문제를 풀기전 그래프의 대한 기본 지식들과 그래프 탐색에 필요한 정보들을 공부 해보았다.
그래프 탐색 기본 개념:
1: https://jin1ib.tistory.com/entry/BFS-DFS-1
2: https://velog.io/@tomato2532/%EA%B7%B8%EB%9E%98%ED%94%84
백준 1991 (트리 순회):
문제 출처: https://www.acmicpc.net/problem/1991
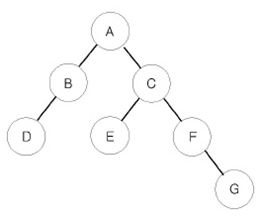
트리 순회 문제 같은 경우 그래프 도 중요 하지만 우선 트리의 개념도 잘 알아둬야 한다. 트리의 개념을 이해하고 순회 하는것을 구상해보면 문제를 생각보다 간단하게 접근 해서 풀수 있다.
트리 개념 참고: https://m.blog.naver.com/rlakk11/60159303809
내 정답 코드)
import sys
N = int(sys.stdin.readline().rstrip())
tree = {}
for i in range(N):
root, left, right = sys.stdin.readline().strip().split()
tree[root] = [left, right]
def preorder(root):
if root != '.':
print(root, end='') # root
preorder(tree[root][0]) # left
preorder(tree[root][1]) # right
def inorder(root):
if root != '.':
inorder(tree[root][0]) # left
print(root, end='') # root
inorder(tree[root][1]) # right
def postorder(root):
if root !='.':
postorder(tree[root][0]) # left
postorder(tree[root][1]) # right
print(root, end='') # root
preorder('A')
print()
inorder('A')
print()백준 5639 (이진 검색 트리):
문제 출처: https://www.acmicpc.net/problem/5639
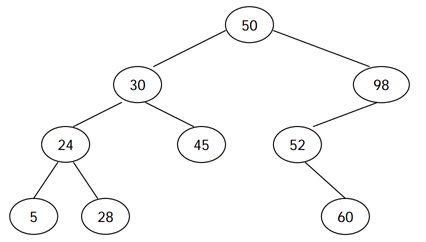
이진 탐색 트리는 이진 탐색 과 연결 리스트의 개념이 합쳐진 것이다. 그래서 각각의 개념과 둘의 연결 관계를 알아야 이 문제를 해결 할수 있다. 처음엔 어떻게 접근해야 할지 몰라서 구글링을 해서 정답 코드를 보면서 문제를 이해 하는 방식으로 풀어 보았다.
코드 참고: https://backtony.github.io/algorithm/2021-02-18-algorithm-boj-class4-20/
내 정답 코드)
import sys
# default 값이 1000이다
sys.setrecursionlimit(10 ** 6)
input = sys.stdin.readline # [50, 30, 24, 5, 28, 45, 98, 52, 60]
def post_order(start, end):
# 역전시 리턴
if start > end:
return
# 루트 노드
root = pre_order[start] # root = 50, root = 30, root = 24, root = 5, root = 28, root = 45, root = 98, root = 52, root = 60 # vertex
idx = start + 1 # idx = 1, idx = 2, idx = 3, idx = 4, idx = 5, idx = 6, idx = 7, idx = 8, idx = 9 # vertex 의 인덱스 번호
# root보다 커지는 지점을 찾는 과정
# for문으로 찾으면 안된다. 아래서 설명
while idx <= end:
if pre_order[idx] > root:
break
idx += 1
# 왼쪽 서브트리
post_order(start + 1, idx - 1)
# 오른쪽 서브트리
post_order(idx, end)
# 후위순회이므로 제일 마지막에 찍으면 된다
print(root) # [5, 28, 24, 45, 30, 60, 52, 98, 50]
pre_order = []
while True:
try:
pre_order.append(int(input()))
# try에서 예외 발생시 break 실행
except:
break
post_order(0, len(pre_order) - 1)백준 1197 (최소 스패닝 트리):
문제 출처: https://www.acmicpc.net/problem/1197
최소 스패닝 트리 문제 같은 경우 kruskal 알고리즘 풀이법 과 prim 알고리즘 풀이법이 있는데 난 kruskal 알고리즘 과 union-find 라는 자료구조를 같이 이용해서 풀었다.
우선 kruskal 알고리즘 의 개념이란?
크루스칼 알고리즘은 가장 적은 간선 비용으로 모든 노드를 연결할수 있도록 하는 알고리즘이다.
그렇다면 크루스칼 알고리즘의 동작방식은 어떻게 진행 될까?
- 주어진 모드 간선 정보에 대해 간선 비용이 낮은 순서(오름차순)로 정렬을 수행
- 정렬된 간선 정보를 하나씩 확인하면서 현재의 간선이 노드들 간의 사이클을 발생시키는지 확인
- 만약 사이클이 발생하지 않은 경우, 최소 신장 트리에 포함시키고 사이클이 발생한 경우, 최소 신장 트리에 포함시키지 않음
- 1번~3번 과정을 모든 간선 정보에 대해 반복 수행
크루스칼 알고리즘 참고: https://techblog-history-younghunjo1.tistory.com/262
위 내용과 같이 크루스칼 알고리즘의 개념과 동작원리에 대해 알아보았다. 이젠 union-find 라는 자료구조의 개념을 알아보자.
union-find 란?
서로 다른 두 개의 집합을 병합하는 Union 연산과 집합의 원소가 어떠한 집합에 속해있는지 판단하는 Find 연산을 지원하기 때문에 Union-Find라는 이름이 나왔다. 여기서 각각의 연산에 대해 설명하자면 다음과 같다:
- Find 연산은 하나의 원소가 어떤 집합에 속해있는지를 판단하는 연산을 말한다.
- Union 연산은 서로 다른 두 개의 집합을 하나의 집합으로 병합하는 연산을 말한다. 이 자료구조에서는 상호 배타적 집합만을 다루므로 Union 연산은 합집합 연산과 동치이다.
union-find 자료구조 참고: https://namu.wiki/w/Union%20Find
내 정답 코드)
import sys
input = lambda: sys.stdin.readline().rstrip()
V, E = map(int, input().split()) # 3, 3
# kruskal algorithm
edges = []
for _ in range(E): # (3)
A, B, C = map(int, input().split()) # A정점, B정점, 가중치
edges.append((A, B, C))
edges.sort(key=lambda x: x[2]) # C(cost)가 적은것부터 정렬
# union-find
parent = [i for i in range(V+1)] # [0, 1, 2, 3]
def get_parent(x):
if parent[x] == x:
return x
parent[x] = get_parent(parent[x]) # get_parent 거슬러 올라가면서 parent[x] 값도 갱신
return parent[x]
def union_parent(a, b):
a = get_parent(a)
b = get_parent(b)
if a < b: # 작은 쪽이 부모가 된다. (한 집합 관계라서 부모가 따로 있는 건 아님)
parent[b] = a
else:
parent[a] = b
def same_parent(a, b):
return get_parent(a) == get_parent(b)
answer = 0
for a, b, cost in edges:
# cost 가 적은 edge부터 하나씩 추가해가면서 같은 부모를 공유하지 않을 때(사이클 없을 때)만 확정
if not same_parent(a, b):
union_parent(a, b)
answer += cost
print(answer)백준 1260 (DFS와 BFS):
문제 출처: https://www.acmicpc.net/problem/1260
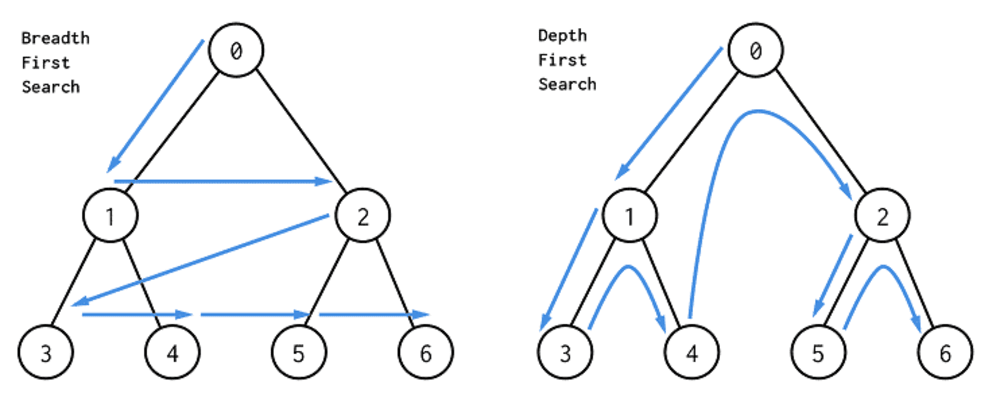
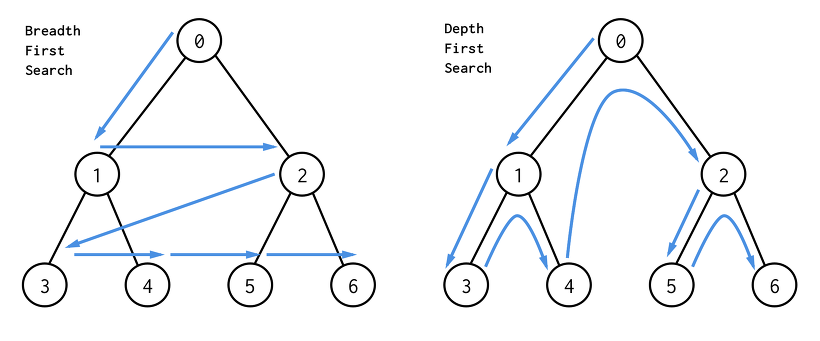
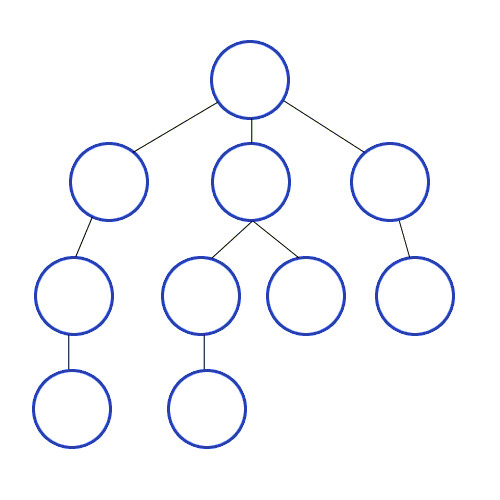
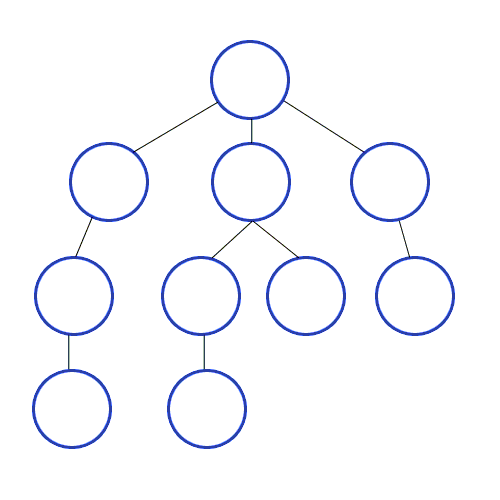
DFS (깊이 우선 탐색), BFS (너비 우선 탐색) 말 그대로 어떤걸 중점으로 두냐에 따라 그래프를 탐색하는 기준이 달라진다. 이미지를 보면 좀더 이해하기 쉬울것 같다. 깊이 우선 탐색인 경우 재귀를 호출 해서 부모 모드 부터 가장 깊숙히 있는 자식노드 까지 우선 탐색한다. 반대로 너비 우선 탐색 같은 경우 부모노드 기준 가장 가까운 하위 노드들을 순차적으로 탐색 하게 된다. 기본적으로 DFS 와 BFS 같은 경우 위 이미지와 같은 그래프 탐색을 기반으로 한 알고리즘 기법 이다. 따라서 이 두가지 유형을 잘 알아 두면 앞으로 많이 그리고 유용하게 사용할수 있을것 같다.
내 정답 코드)
from collections import deque
import sys
input = sys.stdin.readline
def bfs(v):
q = deque()
q.append(v)
visit_list[v] = 1
while q:
v = q.popleft()
print(v, end = " ")
for i in range(1, n + 1): # (1, 5)
if visit_list[i] == 0 and graph[v][i] == 1:
q.append(i)
visit_list[i] = 1
def dfs(v):
visit_list2[v] = 1
print(v, end = " ")
for i in range(1, n + 1):
if visit_list2[i] == 0 and graph[v][i] == 1:
dfs(i)
n, m, v = map(int, input().split()) # 4, 5, 1
graph = [[0] * (n + 1) for _ in range(n + 1)] # [[0, 0, 0, 0, 0], [0, 0, 1, 1, 1], [0, 1, 0, 0, 1], [1, 0, 0, 0, 1], [1, 1, 1, 0, 0]]
visit_list = [0] * (n + 1) # [0, 1, 1, 1, 1]
visit_list2 = [0] * (n + 1) # [0, 1, 1, 1, 1]
for _ in range(m): # (5)
a, b = map(int, input().split()) # (1, 2) (1, 3) (1, 4) (2, 4) (3, 4)
graph[a][b] = graph[b][a] = 1
dfs(v)
print()
bfs(v)백준 11724 (연결 요소의 개수):
문제 출처: https://www.acmicpc.net/problem/11724
연결 요소의 개수 문제 같은 경우 나는 인접리스트로 그래프를 만들고 DFS 로 그래프 탐색을 해보았다. DFS는 재귀적으로 간단하게 구현하고 visited를 선형적으로 탐색하는동안 방문한적 없다면 DFS를 호출 하고 탐색이 끝나면 cnt, 즉 연결 요소 개수를 증가 시킨다.
인접리스트 reference: https://veggie-garden.tistory.com/28
내 정답 코드)
import sys
input = sys.stdin.readline
sys.setrecursionlimit(100000)
N, M = map(int, input().split()) # 6, 5
# 인접 리스트 -> 인덱스를 그대로 정점의 번호를 사용
graph = list([] for _ in range(N+1))
# 연결 요소 개수
cnt = 0
for _ in range(M): # (5)
a, b = map(int, input().split()) # (1, 2) (2, 5) (5, 1) (3, 4) (4, 6)
graph[a].append(b) # graph[[],[2],[],[4],[6],[2,1],[]]
graph[b].append(a) # graph[[],[2,5],[1,5],[4],[3,6],[2,1],[4]]
# DFS
visited = [False] * (N+1) # [False, False, False, False, False, False, False]
def DFS(x):
visited[x] = True # i = 1: [False, True, True, False, False, True, False] => i = 3: [False, True, True, True, True, True, True]
for node in graph[x]:
if not visited[node]:
DFS(node)
cnt = 0
for i in range(1, N+1): #(1, 7)
if not visited[i]:
DFS(i)
cnt += 1 # when True => cnt += 1
print(cnt) # 2- DFS
DFS의 간단한 개념:
1:https://namu.wiki/w/%EA%B9%8A%EC%9D%B4%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89
2:https://velog.io/@changhee09/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-DFS%EA%B9%8A%EC%9D%B4-%EC%9A%B0%EC%84%A0-%ED%83%90%EC%83%89
백준 11725 (트리의 부모 찾기):
문제 출처: https://www.acmicpc.net/problem/11725
트리의 부모 찾기 문제 같은 경우 루트 노드를 제외한 다른 노드들의 부모를 구하는 문제이다. 순서는 다음과 같다:
- 나는 graph를 인접 리스트로 만들고 visited 배열과 parent 배열을 각각 만들어 vistied 배열은 방문처리를 해주고 parent 배열에는 방문한 노드들의 부모노드들 넣어준다.
- DFS 로 진행 해보면 만약 graph의 노드를 방문했을때 방문처리를 해주고 방문한 현재 노드의 부모노드를 아까 만들어둔 parent 배열에 저장 한다. 그리고 DFS 재귀호출을 반복한다.
- 1~2 과정을 반복하면 parent 배열에는 루트 노드를 제외한 다른 노드들의 부모 번호들이 저장 된다.
- parent 리스트를 2번째 부터 출력해주면 된다.
내 정답 코드)
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def dfs(node): # (1)
visited[node] = 1 # visited[1] = 1
for i in graph[node]: # i = 0: graph[1]
if not visited[i]:
parent[i] = node # parent[2] = 4,
dfs(i)
N = int(input()) # 7
graph = [[] for _ in range(N+1)] # [[], [], [], [], [], [], [], []]
visited = [0] * (N+1) # [0, 1, 1, 1, 1, 1, 1, 1]
parent = [0] * (N+1) # [0, 0, 4, 6, 1, 3, 1, 4]
while True:
try:
a, b = map(int, input().split()) # (1,6) (6,3) (3,5) (4,1) (2,4) (4,7)
graph[a].append(b)
graph[b].append(a) # [[], [6,4], [4], [6,5], [1,2,7], [3], [1,3], [4]]
except:
break
for i in range(N+1): # (8)
graph[i].sort() # [[], [4,6], [4], [5,6], [1,2,7], [3], [1,3], [4]]
dfs(1)
print(*parent[2:], sep='\n')백준 1707 (이분 그래프):
문제 출처: https://www.acmicpc.net/problem/1707
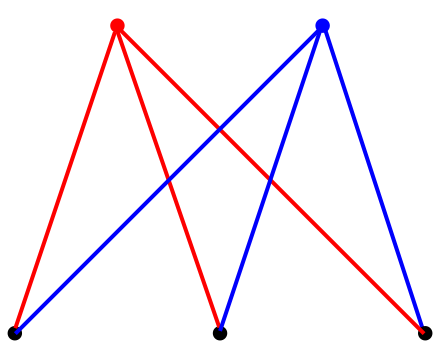
이분 그래프 문제 같은 경우 그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.
해당 문제를 풀때 포인트들은 다음과 같다:
- graph, visited, groups 라는 배열을 만들어준다.
- graph 는 인접리스트로 입력값을 받아와서 만들어주고 visited 는 노드 방문시 방문처리 역할을 해주며 groups는 해당 노드에 방문 했을때 이 노드의 그룹을 지정 해주는것이다.
- 만약 그룹 안에 속한 노드 끼리 서로 인접 하지 않고 분할수 있으면 이분 그래프 이므로 'YES' 로 프린트 출력 해주고 아닐시에 'NO' 로 프린트 출력 해준다.
내 정답 코드)
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def dfs(node, group): # (1,0) (3,1) (2,0) ()
visited[node] = True # visited[1] = True, visited[3] = True, visited[2] = True
groups[node] = group # groups[1] = 0, groups[3] = 1, groups[2] = 0
for next_node in graph[node]: # 3 in graph[1], 1 in graph[3], 2 in graph[3]
if not visited[next_node]: # not visited[3]
if not dfs(next_node, 1 - group): # not dfs(3, 1)
return False
elif groups[next_node] == group:
return False
return True
T = int(input()) # 2
for _ in range(T): # (2)
V, E = map(int, input().split()) # (3,2) and (4,4)
graph = [[] for _ in range(V+1)] # [[],[],[],[]] and [[],[],[],[],[]]
visited = [False] * (V+1) # [False, True, True, True] and [False, False, False, False, False]
groups = [-1] * (V+1) # [-1, 0, 0, 1] and [-1, -1, -1, -1, -1]
for _ in range(E): # (2) and (4)
a, b = map(int, input().split()) # E = 2: (1,3) (2,3), E = 4: (1,2) (2,3) (3,4) (4,2)
graph[a].append(b)
graph[b].append(a) # [[],[3],[3],[1,2]] and [[],[2],[1,3,4],[2,4],[3,2]]
is_bipartite = True
for i in range(1, V + 1): # (1, 4) and (1, 5)
if not visited[i]:
if not dfs(i, 0):
is_bipartite = False
break
if is_bipartite:
print("YES")
else:
print("NO")백준 21606 (아침 산책):
문제 출처: https://www.acmicpc.net/problem/21606
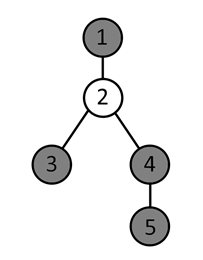
아침 산책 문제 같은 경우 산책 경로가 주어지는데 이때 서로 다른 산책 경로의 경우의 수를 구하는 문제이다.
이 문제를 풀때 포인트들은 다음과 같다:
- 모든 장소를 몇 개의 길을 통해 오고갈 수 있다.
- 아침 산책은 시작점과 도착점을 정하고, 시작점에서 도착점까지 트리 위의 단순 경로(같은 점을 여러 번 지나지 않는 경로)를 따라 걷게 된다.
- 장소는 실내 와 실외로 구분 되며, 산책의 시작점과 끝점이 모두 실내여야 한다. (산책 중간에 실내 장소가 껴있으면 안되고 무조건 시작점과 끝점만 실내여야한다.)
해당 문제 같은 경우
- graph를 인접리스트로 만들고 place 라는 배열을 실내 인지 실외 인지 구분 해주기 위해 만들고 visited 라는 배열을 방문처리용도 로 먼저 만들어준다.
- A 라는 배열에 입력값을 받는데 이때 입력값은 [10111] 이며 1은 실내, 0은 실외를 의미한다. 그리고 만약에 산책 중간에 실내를 만나게 되면 해당 경로는 경우의 수를 포함시키지 않고 다음 경우의 수로 넘어간다.
- graph에 시작점과 끝점을 입력값으로 받아와서 넣고 각 경로를 DFS 로 탐색한다.
- DFS 탐색중 방문하지 않은곳이면 방문처리를 해주고 해당경로를 res 라는 변수에 카운트 1씩 증가 한다.
- 모든 DFS 탐색이 끝난후 경우의 수를 모두 종합하여 나온 값을 ans 라는 변수에 넣어 준다. 이떄 종합 하는 수식은 res * (res - 1) 이렇다. 그 이유는 정점의 개수(N)와 간선의 개수(N-1)를 곱해주는 값이, 곧 모든 경우의 수를 구하는 공식 값과 일치 하기 때문이다.
- 만약 5번에서 실외 가 아니고 실내끼리 연결되어 있는 경우도 경우의 수에 포함 시켜야 하기 때문데 이때도 ans 라는 변수에 카운트 1씩 증가 시킨다.
내 정답 코드)
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
n = int(input()) # 5
A = input().rstrip() # 10111
graph = [[] for _ in range(n+1)] # [[],[],[],[],[],[]]
place = [0] * (n+1) # [0,1,0,1,1,1]
visited = [0] * (n+1) # [0,0,1,0,0,0]
for i in range(len(A)): # (5)
if A[i] == '1':
place[i+1] = 1
for _ in range(n-1):
a, b = map(int, input().split()) # (1, 2) (2, 3) (2, 4) (4, 5)
graph[a].append(b)
graph[b].append(a) # [[],[2],[1,3,4],[2],[2,5],[4]]
def dfs(node):
res = 0
for next_node in graph[node]:
if place[next_node] == 0:
if not visited[next_node]:
visited[next_node] = 1
res += dfs(next_node)
else:
res += 1
return res
ans = 0
for i in range(1, n+1): # (1, 6)
if place[i] == 0:
if not visited[i]:
visited[i] = 1
res = dfs(i)
ans += res * (res - 1)
else:
for next_node in graph[i]:
if place[next_node] == 1:
ans += 1
print(ans)백준 2573 (빙산):
문제 출처: https://www.acmicpc.net/problem/2573
지구 온난화로 인하여 북극의 빙산이 녹고 있다. 빙산을 그림 1과 같이 2차원 배열에 표시한다고 하자. 빙산의 각 부분별 높이 정보는 배열의 각 칸에 양의 정수로 저장된다. 빙산 이외의 바다에 해당되는 칸에는 0이 저장된다. 그림 1에서 빈칸은 모두 0으로 채워져 있다고 생각한다.

빙산의 높이는 바닷물에 많이 접해있는 부분에서 더 빨리 줄어들기 때문에, 배열에서 빙산의 각 부분에 해당되는 칸에 있는 높이는 일년마다 그 칸에 동서남북 네 방향으로 붙어있는 0이 저장된 칸의 개수만큼 줄어든다. 단, 각 칸에 저장된 높이는 0보다 더 줄어들지 않는다. 바닷물은 호수처럼 빙산에 둘러싸여 있을 수도 있다. 따라서 그림 1의 빙산은 일년후에 그림 2와 같이 변형된다.
그림 3은 그림 1의 빙산이 2년 후에 변한 모습을 보여준다. 2차원 배열에서 동서남북 방향으로 붙어있는 칸들은 서로 연결되어 있다고 말한다. 따라서 그림 2의 빙산은 한 덩어리이지만, 그림 3의 빙산은 세 덩어리로 분리되어 있다.
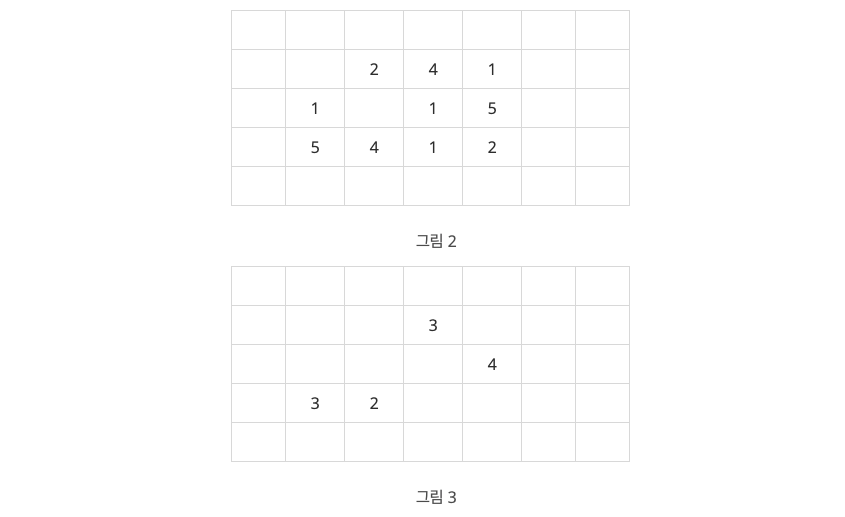
한 덩어리의 빙산이 주어질 때, 이 빙산이 두 덩어리 이상으로 분리되는 최초의 시간(년)을 구하는 프로그램을 작성하시오. 그림 1의 빙산에 대해서는 2가 답이다. 만일 전부 다 녹을 때까지 두 덩어리 이상으로 분리되지 않으면 프로그램은 0을 출력한다.
빙산 문제를 풀때 포인트는 다음과 같다:
- 빙산이 녹는것 처리한다. (한번 녹을때 한꺼번에 녹는 처리가 필요함)
- 빙산의 영역을 체크한다. (영역 체크를 하면서 몇덩어리로 나눠졌는지 체크)
- 빙산의 영역이 두덩이 이상 인지 체크 해서 그때 연도를 출력.
참고: https://velog.io/@nuri00/%EB%B9%99%EC%82%B0
내 정답 코드)
import sys
sys.setrecursionlimit(10**5)
input = sys.stdin.readline
def dfs(x, y):
for direction in range(4):
nx = dx[direction]+x
ny = dy[direction]+y
if 0 <= nx < N and 0 <= ny < M and visited[nx][ny]:
visited[nx][ny] = False
if iceMap[nx][ny] != 0:
dfs(nx, ny)
N, M = map(int, input().split())
iceMap = []
for _ in range(N):
iceMap.append(list(map(int, input().split()))[:M])
year = 0
visited = [[False]*M for _ in range(N)]
dx = [1, -1, 0, 0]
dy = [0, 0, 1, -1]
while True:
year += 1
# 빙산 녹는 처리
for i in range(N):
for j in range(M):
if iceMap[i][j] != 0:
visited[i][j] = True
state = iceMap[i][j]
for k in range(4):
nx = dx[k]+i
ny = dy[k]+j
if 0 <= nx < N and 0 <= ny < M and not visited[nx][ny]:
if iceMap[nx][ny] == 0:
state -= 1
if state == 0:
break
iceMap[i][j] = state
# 빙산 영역 체크
field = 0
for i in range(N):
for j in range(M):
if iceMap[i][j] != 0 and visited[i][j]:
dfs(i, j)
field += 1
elif iceMap[i][j] == 0 and visited[i][j]:
visited[i][j] = False
if field >= 2:
print(year)
break
elif field == 0:
print(0)
break
백준 2617 (구슬 찾기):
문제 출처: https://www.acmicpc.net/problem/2617
구슬 찾기 문제 같은 경우 인접 리스트로 graph 생성후 DFS로 풀어보았다.
접근 방식은 다음과 같다:
-
목표는 특정한 정점이 전체 배열의 정중앙에 위치할 수 있는지 여부를 확인하는 것
- 전체 배열의 정점 개수는 홀수이므로, 정중앙의 인덱스는 N//2
- 정중앙에 위치하는 정점을 정확히 알 수는 없으므로, 정중앙에 위치할 수 없는 정점 을 찾아야 함
-
특정한 정점(v)이 정중앙에 위치할 수 없는 경우는 아래 2개의 상황임
-
v보다 큰 정점 개수가 N//2개를 넘음 (즉, N//2 + 1 이상)
- 오름차순으로 정렬 시 v 뒤에 오는 정점의 개수가 N//2 보다 큼
- 정방향 그래프에서 v를 기준으로 DFS 실행 시 자손의 개수가 N//2 보다 큼
-
본인보다 작은 정점 개수가 N//2개를 넘음
- 내림차순으로 정렬 시 v 뒤에 오는 정점의 개수가 N//2 보다 큼
- 역방향 그래프에서 v를 기준으로 DFS 실행 시 자손의 개수가 N//2 보다 큼
-
내 정답 코드)
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
N, M = map(int, input().split())
graphB = [[] for _ in range(N+1)]
graphS = [[] for _ in range(N+1)]
for _ in range(M):
a, b = map(int, input().split())
graphB[a].append(b)
graphS[b].append(a)
def dfs(graph, vertex):
visit[vertex] = True
for next_vertex in graph[vertex]:
if not visit[next_vertex]:
dfs(graph, next_vertex)
count = 0
for i in range(1, N + 1):
visit = [False] * (N + 1)
dfs(graphB, i)
if sum(visit) - 1 >= N // 2 + 1:
count += 1
else:
visit = [False] * (N + 1)
dfs(graphS, i)
if sum(visit) - 1 >= N // 2 + 1:
count += 1
print(count)- BFS
BFS의 간단한 개념:
1:https://namu.wiki/w/%EB%84%88%EB%B9%84%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89
2:https://velog.io/@akimcse/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-DFSBFS-%EA%B0%84%EB%8B%A8-%EA%B0%9C%EB%85%90-%EC%A0%95%EB%A6%AC
백준 2178 (미로 탐색):
문제 출처: https://www.acmicpc.net/problem/2178
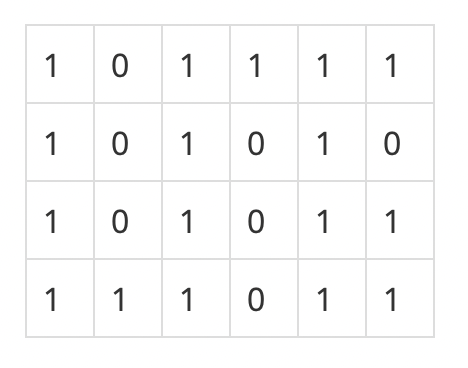
미로 탐색 같은 문제의 경우 그래프의 좌표 값을 받아서 상하좌우를 탐색 하면서 미로를 빠져 나갈수 있는 최소 길이를 구하는 문제이다.
이 문제의 포인트는 다음과 같다:
- 동서남북 방향 정의 및 위치 확인
- 위치이탈이랑 벽에 부딪히면 진행 불가 이므로 조건문 만들기
- 벽이 아닐때 이동 하기
- 마지막 값에서 카운트 값 뽑기
- 초기 값 설정
내 정답 코드)
from collections import deque
N, M = map(int, input().split()) # 4, 6
graph = []
for _ in range(N):
graph.append(list(map(int, input()))) # [[1,0,1,1,1,1],[1,0,1,0,1,0],[1,0,1,0,1,1],[1,1,1,0,1,1]]
def BFS(x, y):
# 이동할 상, 하, 좌, 우 방향 정의
dx = [-1,1,0,0] # 북, 남 => 상, 하
dy = [0,0,-1,1] # 서, 동 => 좌, 우
queue = deque()
queue.append((x,y))
while queue:
x, y = queue.popleft() # 현재 좌표
# 현재 위치에서 4가지 방향 위치 확인
for i in range(4):
nx = x + dx[i] # 상,하 이동
ny = y + dy[i] # 좌,우 이동
# 위치 벗어나면 안되므로 조건 추가 and 벽이므로 진행 불가
if nx<0 or nx>=N or ny<0 or ny>=M or graph[nx][ny]==0:
continue
# 벽이 아니므로 이동 가능
if graph[nx][ny]==1:
graph[nx][ny] = graph[x][y]+1
queue.append((nx,ny))
# 마지막 값에서 카운트 값 뽑기
return graph[N-1][M-1] # 자리에 도달했을때 값을 반환
print(BFS(0,0)) # 초기 값 설정
# [1,0,1,1,1,1] => [3, 0, 9, 10, 11, 12]
# [1,0,1,0,1,0] => [2, 0, 8, 0, 12, 0]
# [1,0,1,0,1,1] => [3, 0, 7, 0, 13, 14]
# [1,1,1,0,1,1] => [4, 5, 6, 0, 14, 15]백준 18352 (특정 거리의 도시 찾기):
문제 출처: https://www.acmicpc.net/problem/18352
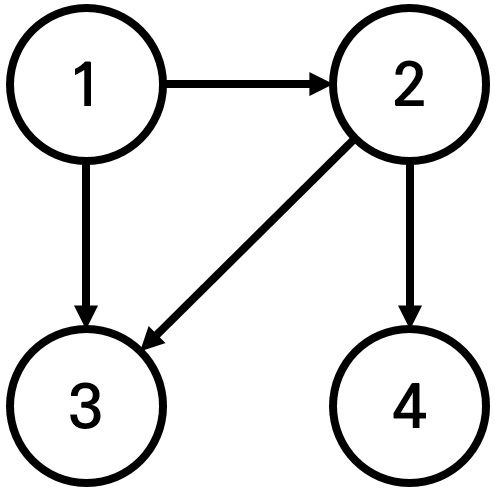
특정 거리의 도시 찾기 문제 같은 경우 최단 거리가 K 인 도시 번호를 구해서 출력 하는 문제이다. 이 문제를 풀때의 포인트는 다음과 같다:
- 모든 도로의 길이는 1이다.
- 1번 도시에서 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 2인 도시는 4번 도시 뿐이다. 2번과 3번 도시의 경우, 최단 거리가 1이기 때문에 출력하지 않는다.
- A => B 도시로 이동 하는 단방향 도로가 존재 한다 (A, B는 서로 다른 자연수 이다.)
- K 거리에 해당하는 도시를 판별 (도시가 존재할 경우와 그렇지 않을경우를 구분해야한다).
내 정답 코드)
import sys
from collections import deque
input = sys.stdin.readline
N, M, K, X = map(int, input().split()) # 도시의 개수, 도로의 개수, 거리 정보, 출발 도시의 번호
graph = [[] for i in range(N+1)] # 그래프 생성
for i in range(M):
A, B = map(int, input().split()) # A => B 도시로 이동하는 단방향 도로가 존재한다. (# A, B는 서로 다른 자연수 이다.)
graph[A].append(B)
d = [-1] * (N+1) # 노드 간 거리 -1로 초기화
d[X] = 0 # 시작 노드의 거리는 0으로
queue = deque([X]) # 시작 노드
while queue:
start = queue.popleft() # 현재 노드 pop
for nx in graph[start]: # 현재 갈 수 있는 모든 노드 탐색
if d[nx] == -1: # 방문한적 없는 노드이면
d[nx] = d[start]+1 # 방문 처리
queue.append(nx)
city = False # K 거리에 해당하는 도시가 있는지 판별
for i in range(1, N+1):
if d[i] == K:
print(i)
city = True # 도시가 존재
if city == False: # 도시가 존재 안할때
print(-1)
백준 1916 (최소 비용 구하기):
문제 출처: https://www.acmicpc.net/problem/1916
최소 비용 구하기 문제 같은 경우 우선 다익스트라 알고리즘을 먼저 알아야 문제를 수월하게 풀수 있다. 그래서 다익스트라 알고리즘이란? (Chat-GPT 에게 물어보았다.)
다익스트라 알고리즘은 최단 경로 문제를 해결하는 그리디 알고리즘이다.
동작 순서를 살펴보면 다음과 같다:
-
출발 노드를 지정하고, 출발 노드로부터 다른 모든 노드까지의 최단 거리를 저장할 거리 배열을 초기화합니다. 출발 노드 자신까지의 거리는 0으로 설정하고, 나머지 거리들은 무한대(혹은 충분히 큰 수)로 초기화합니다.
-
방문하지 않은 노드들 중에서 거리 배열의 값이 가장 작은 노드를 선택합니다. 이 노드는 "현재 노드"라고 부릅니다.
-
현재 노드에 인접한 노드들의 거리 배열 값을 갱신합니다. 즉, 현재 노드에서 인접한 노드로 가는 거리가 더 짧아지면 거리 배열 값을 갱신합니다.
-
현재 노드를 방문한 노드로 체크합니다.
-
모든 노드를 방문할 때까지 2-4 과정을 반복합니다.
다익스트라 알고리즘은 간선 가중치가 음수가 아닌 경우에 사용할 수 있습니다. 이는 "최단 거리의 갱신" 단계에서 현재 노드를 거쳐 가는 경로가 무조건 더 길어지지 않는다는 가정이 필요하기 때문이다.
다익스트라 알고리즘은 시간 복잡도가 O(V^2) 이지만, 우선순위 큐를 사용하여 O(ElogV)까지 최적화할 수 있다.
다익스트라 개념 참고: https://m.blog.naver.com/ndb796/221234424646
내 정답 코드)
import sys
from heapq import heappush, heappop
input = sys.stdin.readline
INF = int(1e9)
N = int(input()) # 5
M = int(input()) # 8
graph = [[] for _ in range(N + 1)] # [[], [], [], [], [], []]
distance = [INF] * (N + 1) # [1000000000, 1000000000, 1000000000, 1000000000, 1000000000, 1000000000]
for i in range(M): # (8)
A, B, C = map(int, input().split()) # (1, 2, 2) (1, 3, 3) (1, 4, 1) (1, 5, 10) (2, 4, 2) (3, 4, 1) (3, 5, 1) (4, 5, 3)
graph[A].append((B, C)) # [[], [(2,2),(3,3),(4,1),(5,10)], [(4,2)], [(4,1),(5,1)], [(5,3)], []]
start, end = map(int, input().split()) # 1, 5
def dijkstra(start): # (1)
q = [(0, start)] # q = [(0, 1)]
distance[start] = 0 # distance[1] = 0 => [1000000000, 0, 1000000000, 1000000000, 1000000000, 1000000000]
while q:
dist, now = heappop(q) # (0, 1) (1, 4) (2, 2) (3, 3) (4, 5) (10, 5)
if distance[now] < dist: # distance[1] < 0
continue
for V, W in graph[now]: # (2,2) in graph[1]
cost = dist + W # cost = 0 + 2
if cost < distance[V]: # 2 < distance[2]
distance[V] = cost # distance[2] = 2
heappush(q, (cost, V)) # (q, (0, 2))
dijkstra(start)
print(distance[end]) # distance의 마지막 인덱스 값 출력 => [1000000000, 0, 2, 3, 1, 4]백준 2665 (미로 만들기):
문제 출처: https://www.acmicpc.net/problem/2665
n×n 바둑판 모양으로 총 n2개의 방이 있다. 일부분은 검은 방이고 나머지는 모두 흰 방이다. 검은 방은 사면이 벽으로 싸여 있어 들어갈 수 없다. 서로 붙어 있는 두 개의 흰 방 사이에는 문이 있어서 지나다닐 수 있다. 윗줄 맨 왼쪽 방은 시작방으로서 항상 흰 방이고, 아랫줄 맨 오른쪽 방은 끝방으로서 역시 흰 방이다.
시작방에서 출발하여 길을 찾아서 끝방으로 가는 것이 목적인데, 아래 그림의 경우에는 시작방에서 끝 방으로 갈 수가 없다. 부득이 검은 방 몇 개를 흰 방으로 바꾸어야 하는데 되도록 적은 수의 방의 색을 바꾸고 싶다.
아래 그림은 n=8인 경우의 한 예이다.
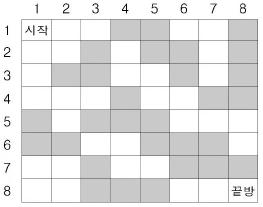
위 그림에서는 두 개의 검은 방(예를 들어 (4,4)의 방과 (7,8)의 방)을 흰 방으로 바꾸면, 시작방에서 끝방으로 갈 수 있지만, 어느 검은 방 하나만을 흰 방으로 바꾸어서는 불가능하다. 검은 방에서 흰 방으로 바꾸어야 할 최소의 수를 구하는 프로그램을 작성하시오.
단, 검은 방을 하나도 흰방으로 바꾸지 않아도 되는 경우는 0이 답이다.
미로 만들기 문제 같은 경우 다익스트라 알고리즘과 힙큐를 사용하면 보다 쉽게 풀수 있다. 우선 아이디어는 다음과 같다:
- room 이라는 배열을 만들어 주고 input 값을 배열에 추가 해준다.
- visited 라는 배열을 방문처리를 위해 만들어 준다.
- 다익스트라 함수를 만들어서 행렬을 이용해서 동서남북 돌아다니면서 방문한다.
- 함수안에 heap 이라는 배열을 만들어서 돌아다니다 검은방을 만났을때 방문처리 및 a += 1 해준다.
- 최종적으로 다익스트라 함수를 호출해서 끝방에 도달하면 검은방을 흰방으로 바꾼 최소의 수를 a 변수에 담아서 출력 한다.
내 정답 코드)
import sys
from heapq import heappush, heappop
input = sys.stdin.readline
N = int(input())
room = []
for _ in range(N):
room.append(list(map(int, input().rstrip())))
visited = [[0] * N for _ in range(N)]
def dijkstra():
dx = [1, -1, 0, 0]
dy = [0, 0, -1, 1]
heap = []
heappush(heap, [0, 0, 0])
visited[0][0] = 1
while heap:
a, x, y = heappop(heap)
if x == N - 1 and y == N - 1:
print(a)
return
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if 0 <= nx < N and 0 <= ny < N and visited[nx][ny] == 0:
visited[nx][ny] = 1
if room[nx][ny] == 0:
heappush(heap, [a + 1, nx, ny])
else:
heappush(heap, [a, nx, ny])
dijkstra()백준 7569 (토마토):
문제 출처: https://www.acmicpc.net/problem/7569
철수의 토마토 농장에서는 토마토를 보관하는 큰 창고를 가지고 있다. 토마토는 아래의 그림과 같이 격자모양 상자의 칸에 하나씩 넣은 다음, 상자들을 수직으로 쌓아 올려서 창고에 보관한다.

창고에 보관되는 토마토들 중에는 잘 익은 것도 있지만, 아직 익지 않은 토마토들도 있을 수 있다. 보관 후 하루가 지나면, 익은 토마토들의 인접한 곳에 있는 익지 않은 토마토들은 익은 토마토의 영향을 받아 익게 된다. 하나의 토마토에 인접한 곳은 위, 아래, 왼쪽, 오른쪽, 앞, 뒤 여섯 방향에 있는 토마토를 의미한다. 대각선 방향에 있는 토마토들에게는 영향을 주지 못하며, 토마토가 혼자 저절로 익는 경우는 없다고 가정한다. 철수는 창고에 보관된 토마토들이 며칠이 지나면 다 익게 되는지 그 최소 일수를 알고 싶어 한다.
토마토를 창고에 보관하는 격자모양의 상자들의 크기와 익은 토마토들과 익지 않은 토마토들의 정보가 주어졌을 때, 며칠이 지나면 토마토들이 모두 익는지, 그 최소 일수를 구하는 프로그램을 작성하라. 단, 상자의 일부 칸에는 토마토가 들어있지 않을 수도 있다.
토마토 문제 같은 경우 3차원 배열을 이용해서 풀어야 하는 문제이다. 이 문제를 풀때 포인트는 다음과 같다:
- 큐를 사용해서 BFS 탐색을 하기 위해 초기 방향 값을 지정해준다.
- BFS 함수 안에 초기 익은 토마토 위치를 큐에 추가해준다. (days = 0값으로 초기화 해준다)
- while 문이 실행 되면서 큐에서 하나의 토마토 정보를 꺼내서 방향 별로 탐색한다.
- 익지 않은 토마토 라면 토마토를 익혀주고 새로 익은 토마토 정보를 큐에 추가 해준다.
(days + 1 씩 해준다.) - 모든 토마토가 익었는지 확인한다. 이때 최소 일수을 반환해준다.
문제를 풀면서 3차원 배열이 나와서 처음엔 3중 for문을 쓰게 되면 시간 초과 또는 메모리 초과가 나지 않을까 라는 생각이 들었지만 예상외로 정답이 나와서 놀랐다. (정말 시간복잡도랑 공간복잡도를 생각하면서 풀기 쉽지 않다,,) 뭔가 노가다 문제 인것 같은 느낌이 많이 드는 문제 였던것 같다.. 3차원 배열은 다시 한번 생각 해봐야겠다.
내 정답 코드)
from collections import deque
m, n, h = map(int, input().split()) # 입력 받기
box = [] # 토마토 상자 정보
for i in range(h):
box.append([list(map(int, input().split())) for j in range(n)])
# 상하좌우, 앞뒤 방향 설정
dh = [-1, 1, 0, 0, 0, 0] # 앞뒤 방향
dn = [0, 0, -1, 1, 0, 0] # 상하 방향
dm = [0, 0, 0, 0, -1, 1] # 좌우 방향
# BFS 함수 정의
def bfs():
# 초기 익은 토마토 위치 큐에 추가
q = deque()
for i in range(h):
for j in range(n):
for k in range(m):
if box[i][j][k] == 1:
q.append((i, j, k, 0))
# BFS 수행
while q:
# 큐에서 하나의 토마토 정보를 꺼냄
th, tn, tm, days = q.popleft()
# 상하좌우, 앞뒤 방향으로 탐색
for i in range(6):
nh = th + dh[i]
nn = tn + dn[i]
nm = tm + dm[i]
# 상자의 범위를 벗어나지 않으면서,
# 익지 않은 토마토 라면
if 0 <= nh < h and 0 <= nn < n and 0 <= nm < m and box[nh][nn][nm] == 0:
# 토마토 익힘
box[nh][nn][nm] = 1
# 새로 익은 토마토 정보 큐에 추가
q.append((nh, nn, nm, days + 1))
# 모든 토마토가 익었는지 확인
for i in range(h):
for j in range(n):
for k in range(m):
if box[i][j][k] == 0:
return -1
# 최소 일수 반환
return days
# BFS 수행
result = bfs()
# 결과 출력
print(result)백준 3055 (탈출):
문제 출처: https://www.acmicpc.net/problem/3055
탈출 문제 같은 경우 처음에 봤을떄 고슴도치와 물이 이동하는것을 어떻게 동시에 처리 할까 라는 의문이 생겼다가 물의 위치가 여러개 일때도 있고 여러 예외사항들이 존재해서 상당히 까다로운 문제라고 생각한다.
해당 문제를 풀때에 다음과 같은 포인트가 있다:
- 물의 위치와 고슴도치 위치 추적.
(물의 위치가 여러개 일 경우도 있으니 나 같은 경우 deque의 특성중 하나인 appendleft를 사용하였다.) - 큐 안에있는 물 과 고슴도치의 위치정보들을 각각 while문 안에서 방향이동을 하며 예외처리 진행. (자세한 예외처리 내용은 코드 옆에서 주석으로 남겨 놓음)
- 예외처리 후 비버의 굴을 도착 했을때 방문처리 및 해당 위치를 q 에 저장후 나중에 출력
- 만약 안전 하게 갈수 없는 경우 while문이 끝나는 시점에 KAKTUS 값을 리턴
내 정답 코드)
from collections import deque
r, c = map(int, input().split()) # 3, 3
graph = [list(input()) for _ in range(r)] # [['D', '.', '*'], ['.', '.', '.'], ['.', 'S', '.']]
visited = [[-1] * c for _ in range(r)] # [[-1, -1, -1], [-1, -1, -1], [-1, -1, -1]]
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
def bfs():
q = deque()
for i in range(r):
for j in range(c):
if graph[i][j] == "*": # 물의 위치
q.appendleft((i, j)) # *** 물의 위치가 여러개 일 경우 q에 모두 추가 해줘야함 ***
visited[i][j] = 0 # 물 방문 처리
elif graph[i][j] == "S": # 고슴도치의 위치
q.append((i, j))
visited[i][j] = 0 # 고슴도치 방문처리
while q:
x, y = q.popleft()
for i in range(4): # 방향 이동
nx, ny = x + dx[i], y + dy[i] # 물, 고슴도치 이동했을때 위치
if not 0 <= nx < r or not 0 <= ny < c: # 범위 밖에 안벗어난 경우
continue
if visited[nx][ny] != -1: # 이동하는 다음 위치에 방문 안했을경우
continue
if graph[nx][ny] == "*" or graph[nx][ny] == "X": # 이동한 다음 위치가 물이 차있거나 돌 인경우 // 예외 처리
continue
if graph[nx][ny] == "D" and graph[x][y] == "*": # 이동한 다음 위치가 비버의 굴이고 물이 차있는 경우 // 예외 처리
continue
if graph[nx][ny] == "D" and graph[x][y] == "S": # 이동한 다음 위치가 비버의 굴이고 고슴도치의 위치인 경우 // 결과값 구하기
return visited[x][y] + 1 # 비버의 굴을 도착했으니 + 1 해주고 방문처리 완료 및 성공
q.append((nx, ny)) # 이동한 위치 q에 저장
visited[nx][ny] = visited[x][y] + 1 # 거리 1씩 증가
graph[nx][ny] = graph[x][y] # 이동한 위치로 변경
return "KAKTUS" # 안전하게 비버의 굴로 이동 불가능
result = bfs() # 최소 거리 결과 저장
print(result) # 결과값 출력백준 2294 (동전 2):
문제 출처: https://www.acmicpc.net/problem/2294
동전 2 문제 같은 경우 코인의 합이 맞으면서 사용한 코인이 최소 개수일때를 구하는 문제이다.
생각 보다 간단한 문제 인거 같지만 실제로 난 예외 처리 때문에 애를 좀 먹었다. (불가능한 경우에 -1을 예외 처리를 해주어야 했는데 그걸 못본 바보 같은 나,,) 중간중간 Chat-GPT를 써보면서 예외처리가 빠졌다는걸 알게 되고 바로 넣어주니 백준에서 정답이 나왔다,,,
이 문제는 DP 로 푼 사람이 생각 보다 많은것 같은데 난 큐 와 BFS를 사용해서 풀었다.
내 정답 코드)
import sys
from collections import deque
n, k = map(int, sys.stdin.readline().split()) # 3, 15
coins = []
for i in range(n): # (3)
coins.append(int(sys.stdin.readline())) # [1, 5, 12]
visited = [False] * 1000001
q = deque()
q.append((0, 0))
while q:
cnt, cur = q.popleft()
if cur == k: # 가능한 경우
print(cnt) # 최소 개수 출력
break
for coin in coins:
if cur + coin <= k and not visited[cur + coin]:
visited[cur + coin] = True # 방문처리
q.append((cnt+1, cur+coin))
if cur != k: # 불가능한 경우 -1 출력 // ** 예외 처리
print(-1)
- 위상 정렬
위상 정렬 문제를 접해 보기전 개념을 먼저 살펴 보자면 위상 정렬이란?
위상 정렬(topological sort)은 방향 그래프에서 각 노드(node)가 다른 노드에 선행(preceding)되는 순서를 찾는 알고리즘입니다. 즉, 노드 간의 의존성(dependency)을 고려하여 그래프의 모든 노드를 선행 순서에 따라 나열하는 것이다.
예를 들어, 대학교에서 과목을 수강할 때, 선행 과목을 먼저 수강해야 하는 경우가 있는데. 이때, 선행 과목을 모두 수강한 후에 수강할 수 있는 과목의 순서를 위상 정렬을 통해 구할 수 있다.
위상 정렬 알고리즘은 일반적으로 DFS(Depth-First Search)나 BFS(Breadth-First Search)와 같은 그래프 탐색 알고리즘을 기반으로 한다. DFS를 이용하여 노드를 탐색할 때, 해당 노드의 모든 선행 노드들이 이미 방문되었는지 확인하고, 방문되지 않은 선행 노드가 있다면 해당 노드를 먼저 방문한다. 이러한 과정을 모든 노드에 대해 반복하여 위상 정렬 결과를 얻을 수 있다.
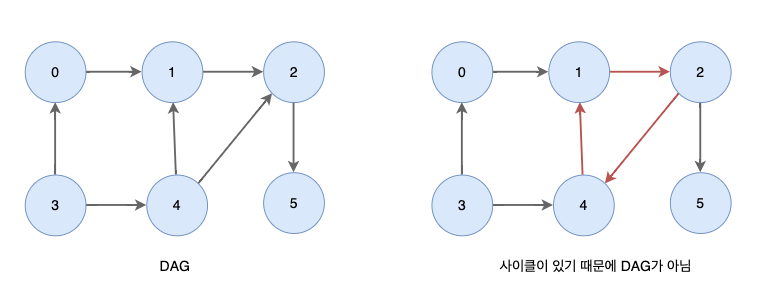
위상 정렬은 사이클이 없는(DAG: Directed Acyclic Graph) 방향 그래프에서만 가능하다. DAG가 아닌 그래프에서는 위상 정렬을 수행할 수 없다.
위상 정렬의 간단한 개념:
1:https://oi.readthedocs.io/en/latest/ds&algo/others/topological_sort.html
2:https://yoongrammer.tistory.com/86
백준 2252 (줄 세우기):
문제 출처: https://www.acmicpc.net/problem/2252
줄 세우기 문제 같은 경우 위상정렬과 스택을 이용해서 풀었다. 우선 위상정렬을 쓰려면 다음과 전제 조건이 필요하다:
- DAG (Directed Acyclic Graph) 비순환 방향 그래프 여야 한다.
- 시작 노드에서 다른 노드로 선행 하는 순서를 찾을때 노드간의 의존성(dependency)을 고려해야 한다.
위 2가지를 바탕으로 스택에 진입 차수가 0인 정점을 추가 해주고 스택에 있는 값을 result 리스트에다가 저장 해주고 result 리스트의 길이와 그 안에 값을 각각 출력해주면 되는 문제이다. 생각 보다 개념은 그리 어렵지 않지만 막상 코드로 접했을때는 쉽지 않다,,
내 정답 코드)
from collections import deque
import sys
input = sys.stdin.readline
N, M = map(int, input().split())
graph = [[] for _ in range(N+1)]
indegree = [0] * (N+1)
# 그래프와 진입차수 초기화
for i in range(M):
A, B = map(int, input().strip().split())
graph[A].append(B)
indegree[B] += 1
print(indegree)
# 위상정렬
def Topological_sort(graph, indegree):
result = []
q = deque()
# 진입차수가 0인 정점을 스택에 추가.
for i in range(1, len(indegree)):
if indegree[i] == 0:
q.append(i)
# 스택이 빌 때까지 반복.
while q:
node = q.popleft()
result.append(node)
# 해당 정점에서 출발하는 모든 간선을 제거.
for v in graph[node]:
indegree[v] -= 1
# 진입차수가 0인 정점을 스택에 추가
if indegree[v] == 0:
q.append(v)
return result
# 위상 정렬 수행
result = Topological_sort(graph, indegree)
# 결과 출력
if len(result) == N:
print(*result)
else:
print('해당 그래프는 DAG가 아닙니다.')
