1.1 수학과 파이썬 복습
벡터와 행렬
신경망에서는 벡터와 행렬 또는 텐서가 등장함.
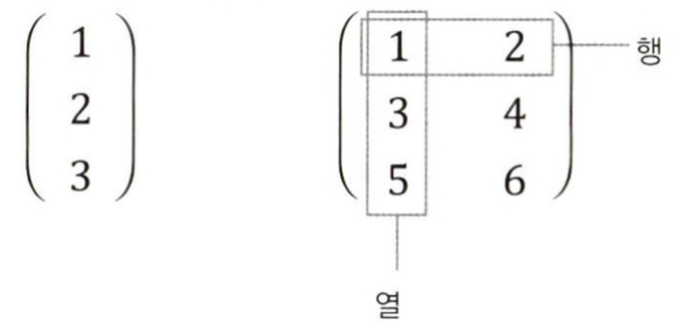
3행 2열(3 X 2) 행렬이다.
- 벡터 : 1차원 배열로 표현 가능
- 행렬 : 2차원 배열로 표현 가능
- 가로줄 : 행(row)
- 세로줄 : 열(column)
벡터를 표현하는 방법은 두 가지이므로 주의해야 한다.
- 숫자들을 세로로 나열하는 방법 (열벡터).
- 숫자들을 가로로 나열하는 방법 (행벡터).
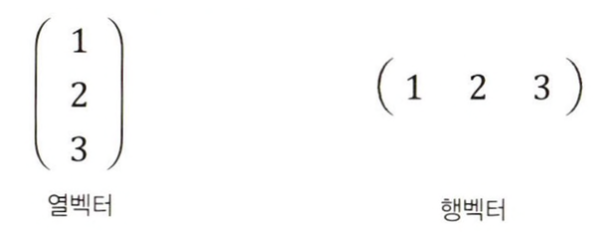
수학과 딥러닝 등 많은 분야에서는 열벡터 방식을 선호함.
다음은 앞에서 다룬 벡터와 행렬의 코드 예시이다.
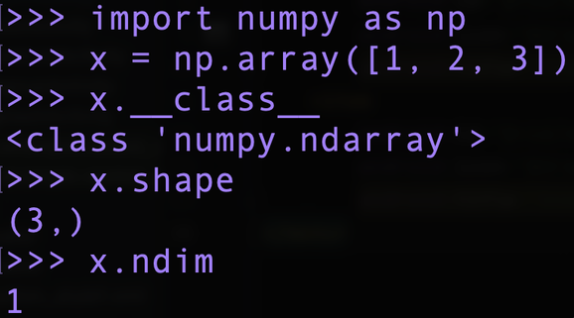
벡터와 행렬 (넘파이 배열)은 np.array() 메서드로 생성 가능하며, shape으로 다차원 배열의 형상을, ndim은 차원 수를 출력해준다.
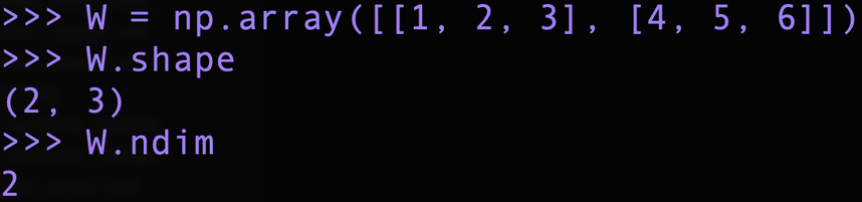
2차원 배열, 2X3 행렬임을 알 수 있다.
원소별 연산 - 넘파이 배열의 사칙연산 예시
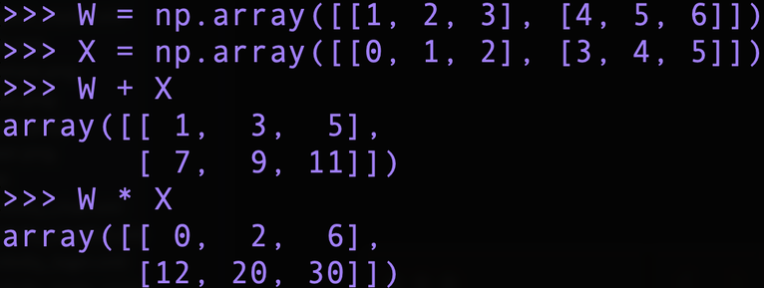
두 넘파이 배열 W, X 의 더하기(+) 와 곱하기(*) 를 해보았다.
실행 결과로 알 수 있는 부분은 다차원 배열들에서 서로 대응하는 원소끼리 (각 원소가 독립적으로) 연산이 이루어진다는 것이다.
브로드캐스트
넘파이의 다차원 배열에서는 형상이 다른 배열끼리 연산이 가능하다.
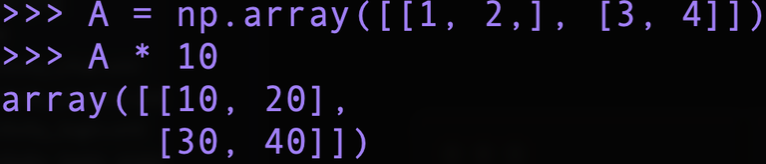
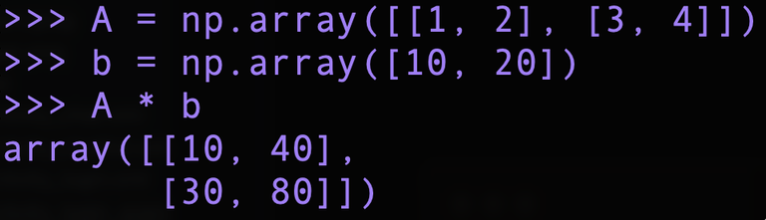
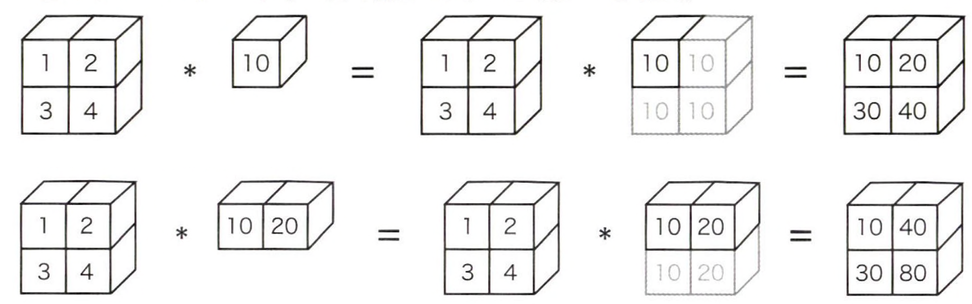
위의 그림에서와 같이 2 X 2 행렬 A에 10이라는 스칼라 값을 곱하였고, 이렇게 하면 스칼라 값 10이 2 X 2 행렬로 확장된 후에 원소별 연산을 수행하는데, 이를 브로드캐스트라 한다.
벡터의 내적
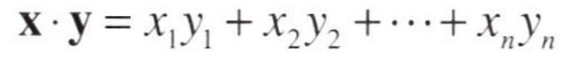
벡터의 내적은 두 벡터에서 대응하는 원소들의 곱을 모두 더한 것으로, 수식은 위의 그림과 같다.
벡터의 내적은 직관적으로는 두 벡터가 얼마나 같은 방향을 향하고 있는가를 나타낸다. 벡터의 길이가 1인 경우로 한정한다면, 완전히 같은 방향을 향하는 두 벡터의 내적은 1이고, 반대 방향을 향하는 두 벡터의 내적은 -1이다.
행렬의 곱
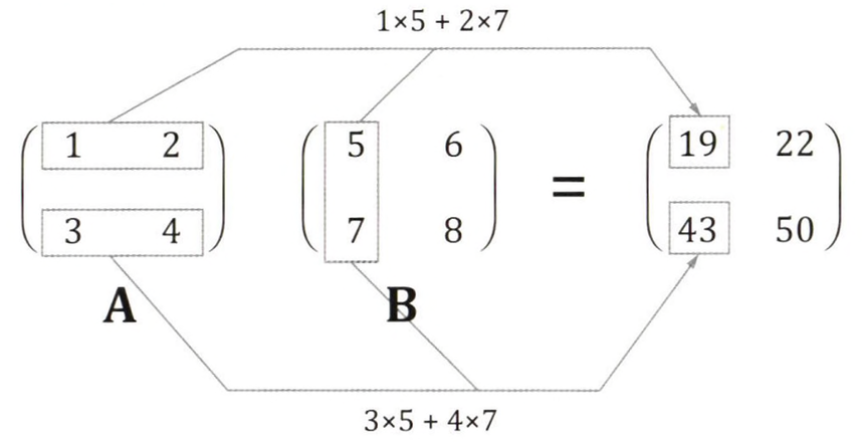
행렬의 곱은 왼쪽 행렬의 행벡터(가로 방향), 오른쪽 행렬의 열벡터(세로 방향)의 내적으로 계산한다.
A의 2행과 B의 1열의 계산 결과는 2행 1열 위치의 원소가 되는 식으로 계산이 수행된다.
아래는 벡터의 내적과 행렬의 곱의 코드 구현이다. 넘파이의 np.dot()과 np.matmul()메서드를 이용하여 쉽게 구현 가능하다.

벡터의 내적 : np.dot()
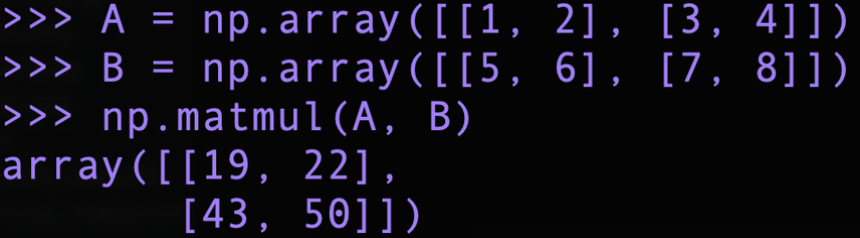
행렬의 곱 : np.matmul()
벡터의 내적과 행렬의 곱 모두에 np.dot()메소드를 사용 가능하지만, 둘을 구분하여 코드의 논리와 의도를 명확하게 구분해주는 것이 좋다.
행렬 형상 확인
행렬이나 벡터를 사용하여 계산 시에는 그 형상에 주의해야 한다. (신경망 구현 시 중요)
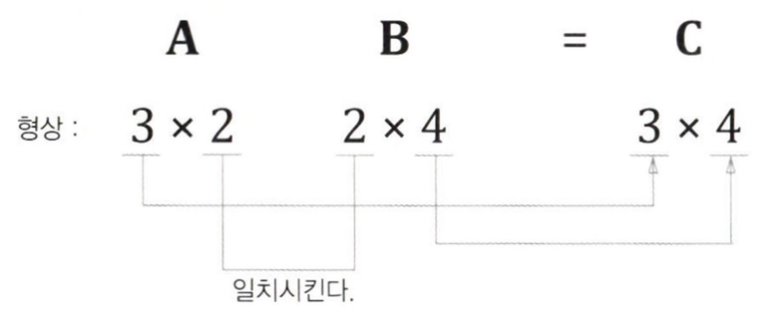
위의 그림처럼 행렬 A 와 B가 대응하는 차원의 원소 수가 같아야 한다. 그리고 결과로 만들어진 행렬 C의 형상은 A의 행 수와 B의 열 수가 된다. → 형상 확인
1.2 신경망의 추론
신경망 추론 전체 그림
신경망은 간단히 말해 단순한 함수라고 할 수 있다. → 함수와 같이 입력을 출력으로 변환한다.
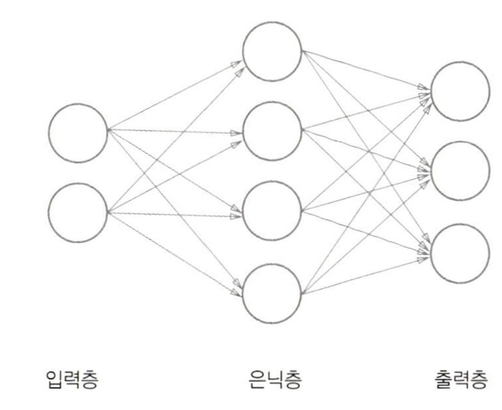
신경망에서의 각 층 사이에 가중치(weight), 편향(bias) 이 존재한다.
위의 그림과 같은 신경망은 인접하는 층의 모든 뉴런과 연결되어 있다는 뜻에서 완전연결계층(fully connected layer) 라고 한다.
임의의 한 층 (x1, x2)에서 다음 은닉층으로의 변환을 다음과 같이 정리할 수 있다.

(1X2) (2X4) → 1X4 + (b1, b2, b3, b4)
이 식은 다음과 같이 간소화 할 수 있다.
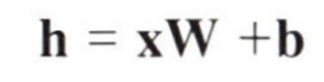
x는 입력, h는 은닉층의 뉴런, W는 가중치, b는 편향을 뜻한다.
앞에서는 하나의 샘플 데이터를 대상으로 하였다. 만약 N개의 샘플 데이터를 미니배치로 한번에 처리한다면 아래와 같이 된다.
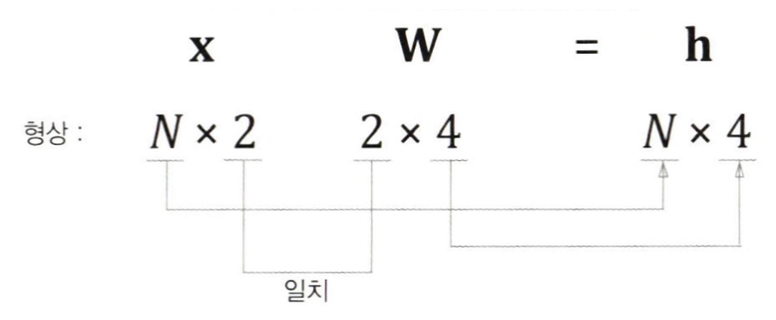
행렬의 형상에 주목하자.
그러므로 형상 확인을 통해 각 미니배치가 올바르게 변환되었는지를 알 수 있다. 이 때 N개의 샘플 데이터가 한꺼번에 완전연결계층에 의해 변환되고, 은닉층에는 N개 분의 뉴런이 함께 계산된다.
변환의 미니배치 버전을 코드로 구현해보았다.
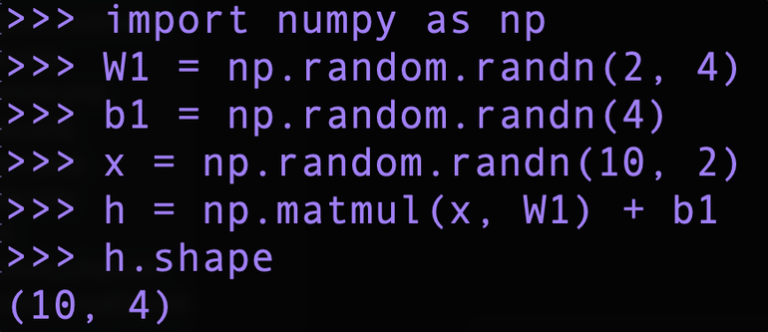
W1 : 가중치, b1 : 편향, x : 미니배치 입력, h : 은닉층 뉴런
이 코드의 마지막 줄에서 b1의 덧셈은 브로드캐스트 된다!
지금까지의 변환은 모두 선형 변환이었다. 여기에 비선형 효과를 부여하는 것이 활성화 함수인데, 이로서 신경망의 표현력을 높일 수 있다. 예를들어 시그모이드 함수가 있다.
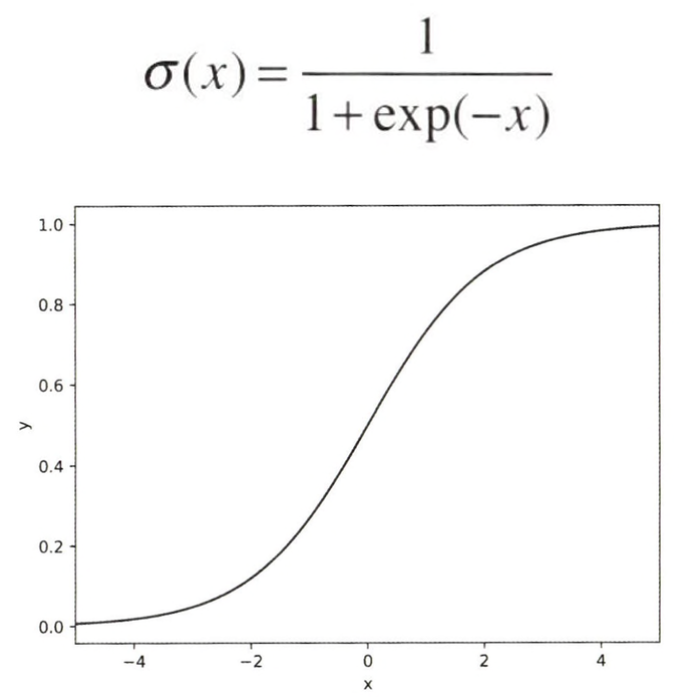
시그모이드 함수는 임의의 실수를 입력받아 0에서 1 사이의 실수를 출력한다. 코드로 구현해보자.
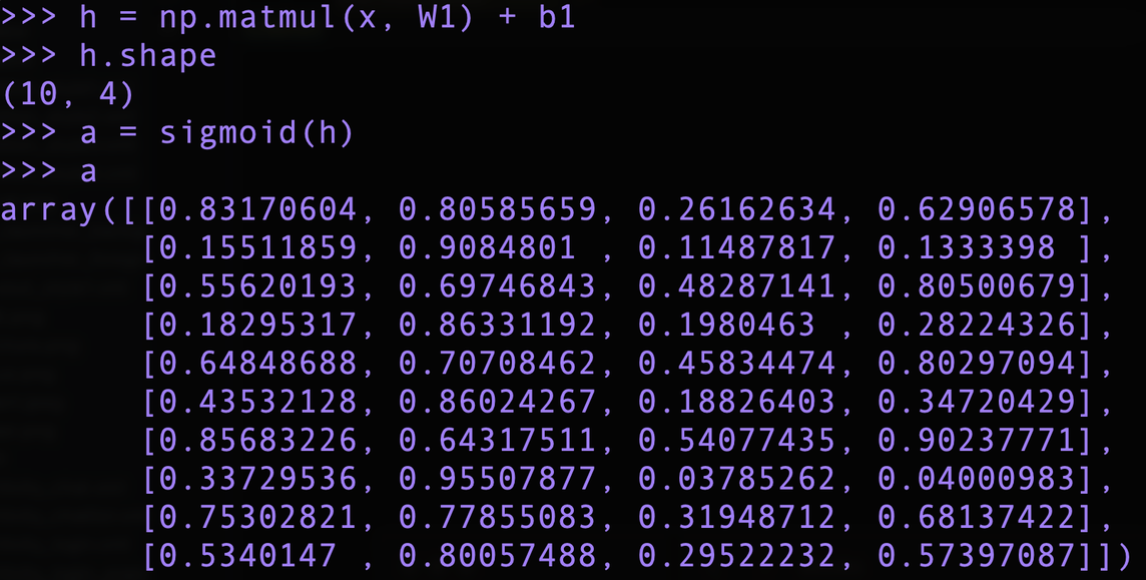
이로서 시그모이드 함수에 의해 비선형 변환이 가능해졌다. 그렇다면 처음의 신경망 이미지를 참고하여 종합적으로 코드로 구현해보자.
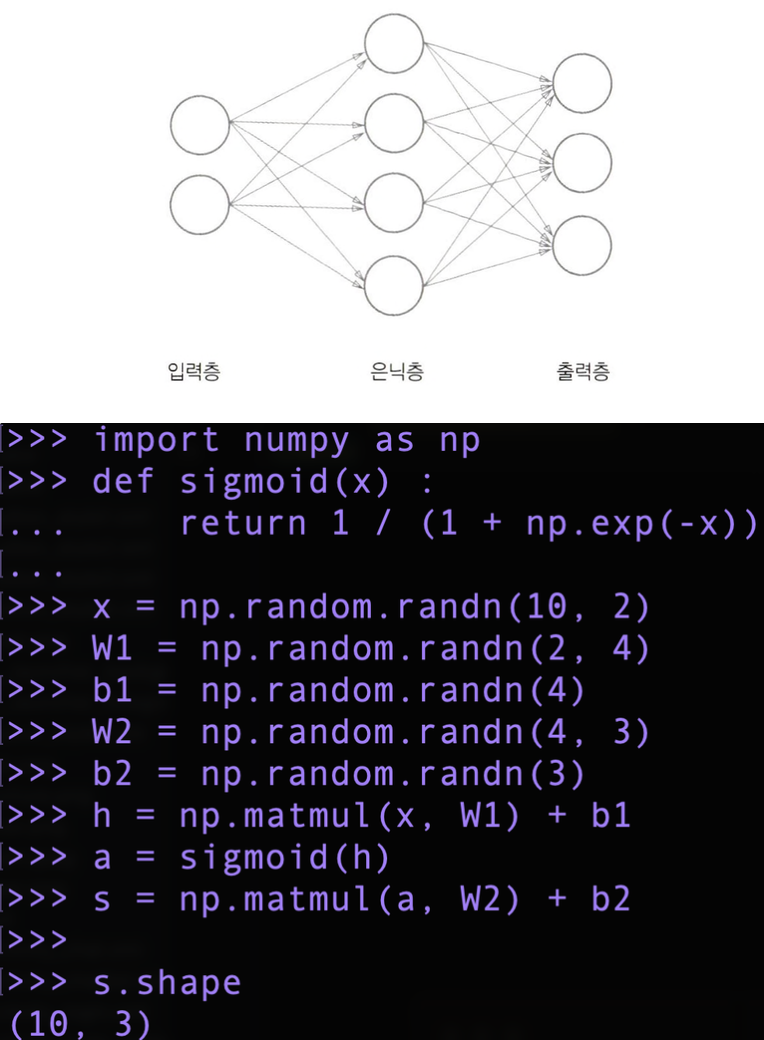
먼저 x의 형상은 (10, 2)이다. 그리고 최종 출력 s의 형상은 (10, 3)이다. 여기서 10개의 데이터가 한번에 처리되었으며 각 데이터는 3차원 데이터로 변환되었다는 것을 의미한다.
이 때 마지막으로 출력된 3차원 데이터는 각 차원의 값을 이용하여 3개 클래스 분류가 가능해진다.
- 각 차원 → 각 클래스에 대응하는 점수(score)
- 실제로 분류를 한다면 출력층에서 가장 큰 값을 내뱉는 뉴런에 해당하는 클래스가 예측 결과가 되는 것이다.
- 점수란 확률이 되기 전의 값이다. 점수가 높을수록 그 뉴런에 해당하는 클래스의 확률도 높아진다.
- 확률은 소프트맥스(Softmax) 함수에 입력 시 얻을 수 있다.
- 실제로 분류를 한다면 출력층에서 가장 큰 값을 내뱉는 뉴런에 해당하는 클래스가 예측 결과가 되는 것이다.
계층으로 클래스화 및 순전파 구현
먼저 구현 규칙 두가지를 보자.
- 모든 계층은
forward()와backward()메서드를 가진다.forward(): 순전파backward(): 역전파
- 모든 계층은 인스턴스 변수인 params와 grads를 가진다.
params: weights, bias와 같은 매개변수를 담는 리스트grads:params에 저장된 각 매개변수에 대응하여 해당 매개변수의 기울기를 보관하는 리스트이다.
이 구현 규칙에 따라 계층들을 구현해보자.
Sigmoid 계층
import numpy as np
class Sigmoid :
def __init__(self) :
self.params = []
def forward(self, x) :
return 1 / (1 + np.exp(-x))- Sigmoid계층에는 학습하는 매개변수가 따로 없으므로 인스턴스 변수인 params는 빈 리스트로 초기화한다.
Affine 계층
class Affine :
def __init__ (self, W, b) :
self.params = [W, b]
def forward(self, x) :
W, b = self.params
out = np.matmul(x, W) + b
return out
- Affine 계층은 초기화될 때 가중치와 편향을 받는다. 즉 가중치와 편향은 Affine 계층의 매개변수이며(이 두 매개변수는 신경망 학습 시 수시로 갱신된다.), 리스트인 params 인스턴스 변수에 보관한다. 다음으로 forward(x)는 순전파 처리를 구현한다.
이제 신경망의 추론 처리를 구현해보자. (신경망 구현)
구현해볼 신경망의 계층 구성은 다음과 같다.
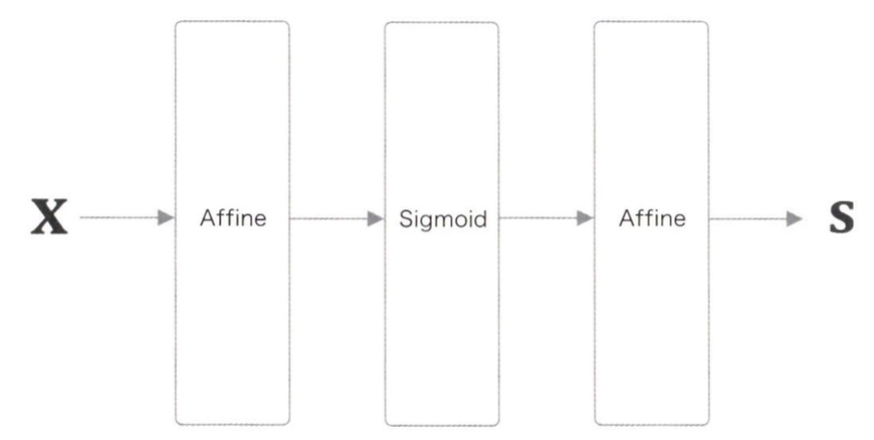
이 신경망을 TwoLayerNet이라는 클래스로 추상화하고, 주 추론 처리는 predict(x) 메서드로 구현해보겠다.
class TwoLayerNet :
def __init__ (self, input_size, hidden_size, output_size) :
I, H, O = input_size, hidden_size, output_size
# 가중치와 편향 초기화
W1 = np.random.randn(I, H)
b1 = np.random.randn(H)
W2 = np.random.randn(H, O)
b2 = np.random.randn(O)
# 계층 생성
self.layers = [
Affine(W1, b1),
Sigmoid(),
Affine(W2, b2)
]
# 모든 가중치를 리스트에 모은다.
self.params = []
for layer in self.layers :
self.params += layer.params
def predict(self, x) :
for layer in self.layers :
x = layer.forward(x)
return x- 모든 학습 매개변수를 하나의 리스트에 담아 보관하면 매개변수 갱신과 매개변수 저장을 손쉽게 처리 가능하다.
x = np.random.randn(10, 2)
model = TwoLayerNet(2, 4, 3)
s = model.predict(x)- 이상으로 입력 데이터 x에 대한 점수(s)를 구할 수 있다.
이처럼 계층을 클래스로 만들어두면 신경망을 쉽게 구현 가능하다. 또한 학습해야 할 모든 매개변수가 model.params 라는 리스트에 모여있기 때문에 이어서 설명할 신경망 학습이 한결 수월해진다.
1.3 신경망의 학습
손실함수
신경망 학습에는 학습이 얼마나 잘 되고 있는지를 알기 위한 척도가 필요하다.
일반적으로 학습 단계의 특정 시점에서 신경망의 성능을 나타내는 척도로 손실(loss)을 사용한다.
손실은 학습 데이터(학습 시 주어진 정답 데이터)와 신경망이 예측한 결과를 비교하여 예측이 얼마나 나쁜가를 산출한 단일 값이다.
신경망의 손실은 손실 함수(loss function)를 사용하여 구한다. 다중 클래스 분류 신경망에서는 손실 함수로 흔히 교차 엔트로피 오차(Cross Entropy Error)를 이용한다. 이 Cross Entropy Error는 신경망이 출력하는 각 클래스의 확률과 정답 레이블을 이용하여 구할 수 있다.
그럼 우리가 지금까지 다뤄온 신경망에서 손실을 구해보자.
- Softmax계층 추가
- Cross Entropy Error 계층 추가
신경망의 계층 구성은 다음과 같아진다.

이 때 X는 입력 데이터, t는 정답 레이블, L은 손실을 의미한다. 이때 Softmax계층의 출력은 확률이 되어 다음계층인 Cross Entropy Error계층에는 확률과 정답 레이블이 입력된다.
소프트맥스 함수
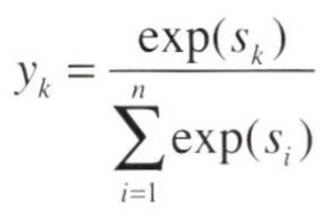
CEE (Cross Entropy Eror)
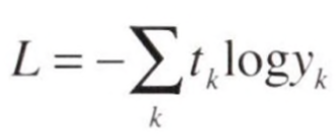
여기서 CEE의 수식을 미니배치 처리를 고려하여 작성하면
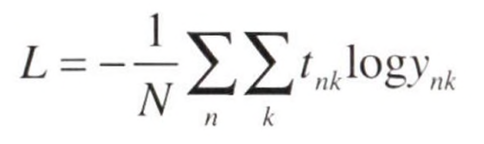
과 같이 된다. 이 식에서 데이터는 N개이며 t_nk는 n번째 데이터의 k차원째의 값을 의미하고 y_nk는 신경망의 출력, t_nk는 정답 레이블을 의미한다.
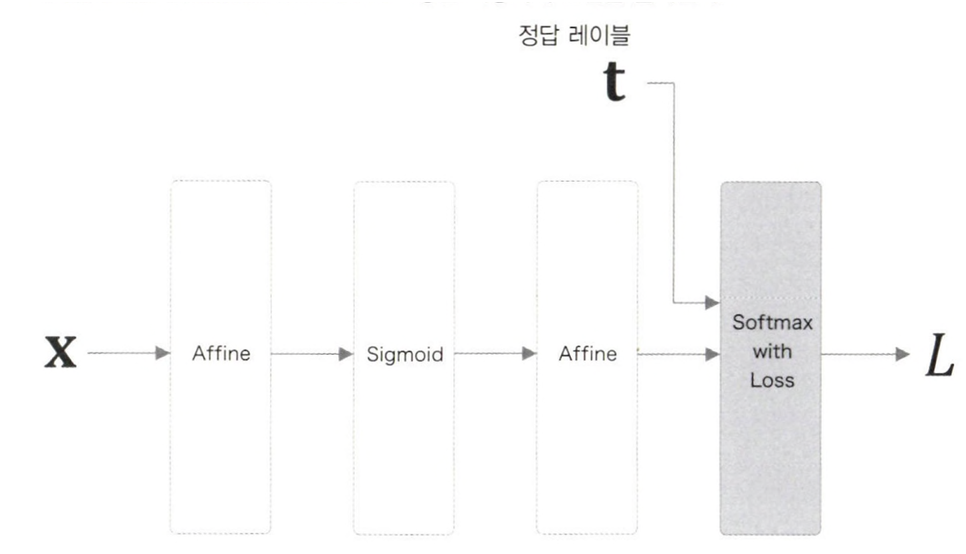
→ Softmax with Loss 계층을 이용하여 손실을 출력한다.
미분과 기울기
어떠한 함수 y = f(x) 가 있다고 가정할 때, x에 관한 y의 미분은 dy/dx 라고 쓴다. 이 dy/dx가 의미하는 것은 x의 값을 조금 변화시켰을 때 y값이 얼마나 변하는가이다. (변화의 정도)
여러 개의 변수(다변수)라도 마찬가지로 미분이 가능한데, 예를들어 L은 스칼라, x는 벡터인 함수 L = f(x)가 있다.
이때 x의 n번째 원소인 x_n에 대한 L의 미분은
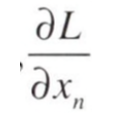
로 쓸 수 있다. 이를 다음과 같이 정리할 수 있다.
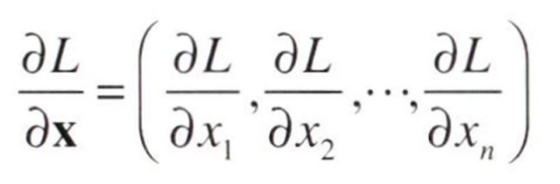
이처럼 벡터의 각 원소에 대한 미분을 정리한 것이 기울기(gradient) 이다.
벡터와 마찬가지로, 행렬에서도 기울기를 생각할 수 있다. 만약 W가 mXn 행렬이라면,
L = g(W) 함수의 기울기는 다음과 같이 쓸 수 있다.
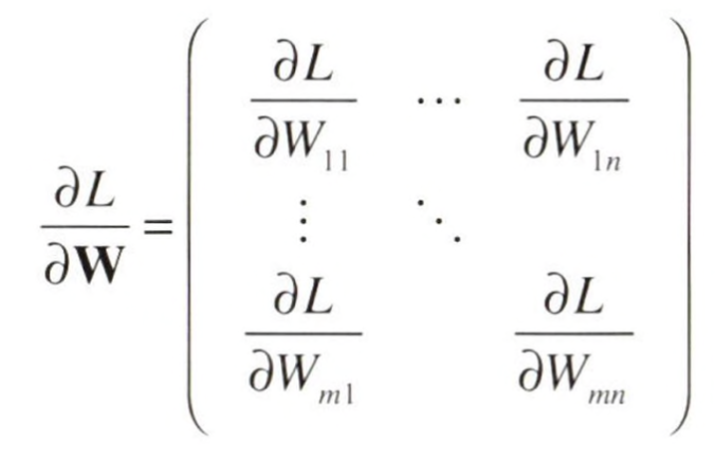
연쇄 법칙
신경망의 기울기를 구하는 법?
오차역전파법(back-propagation)이 등장한다.
- 이를 이해하기 위해서는 연쇄 법칙(chain rule)을 알 필요가 있다.
y = f(x), z = g(y)라는 두 함수가 있다. 그렇다면
z = g(f(x))가 되어 최종 출력 z 는 두 함수를 조합하여 계산 가능하다.

- 다루는 함수가 아무리 복잡하다 하더라도, 즉 아무리 많은 함수를 연결하더라도 그 미분은 개별 함수의 미분들을 이용하여 구할 수 있다.
- 각 함수의 국소적인 미분을 계산 가능하다면 그 값들을 곱하여 전체의 미분을 구할 수 있다.
계산 그래프
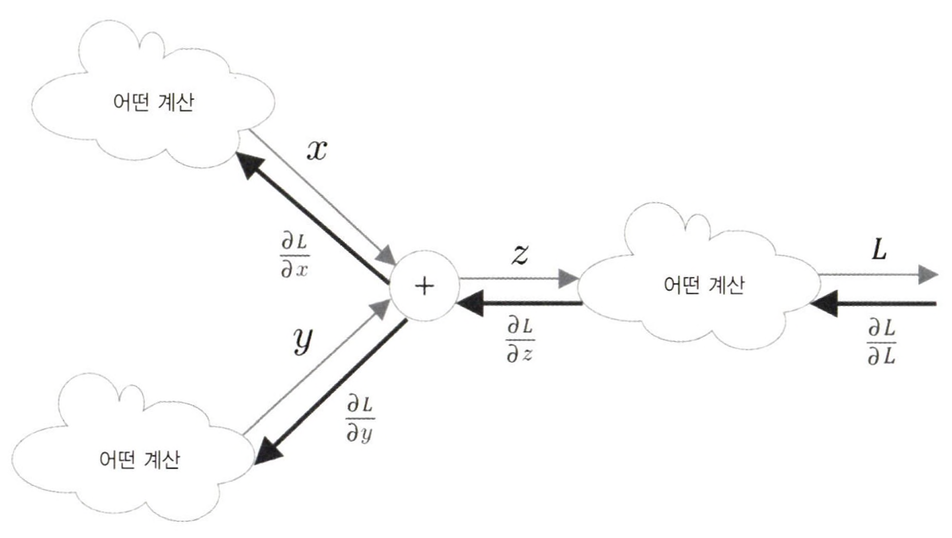
z = x + y
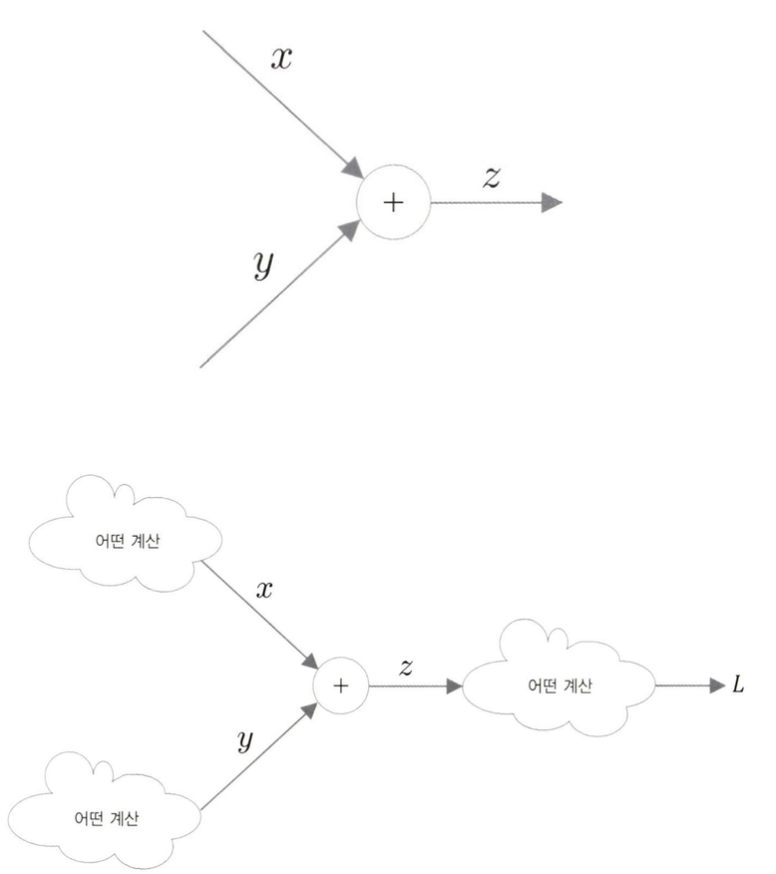
우리의 목표는 L의 미분(기울기)을 각 변수에 대해 구하는 것이다. 그러면 계산 그래프의 역전파는 아래와 같이 그릴 수 있다.
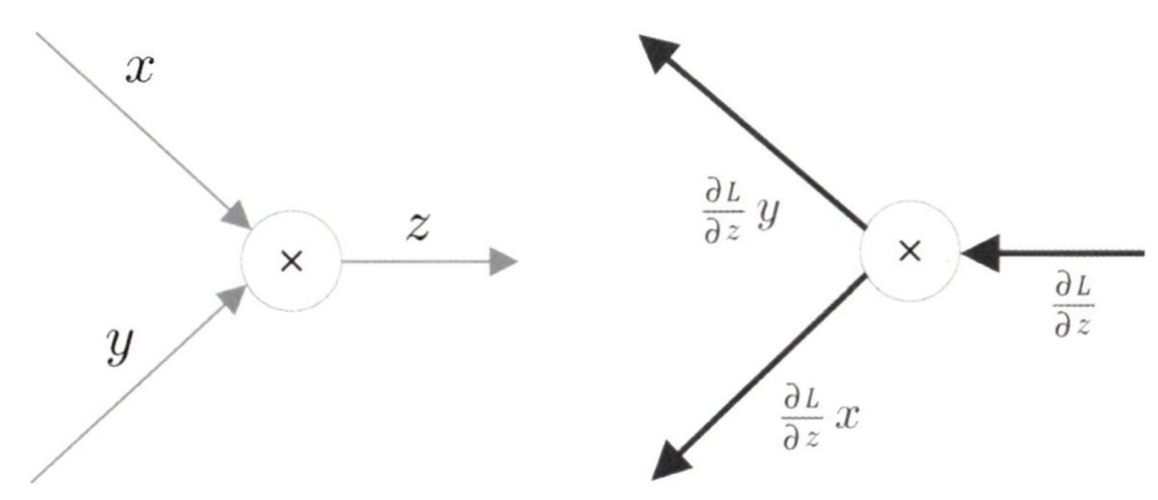
곱셈 노드
곱셈 노드는 z = x * y 계산을 수행한다. 이때 z에 대한 x로의 미분값은 y, z에 대한 y로의 미분값은 x라는 결과를 각각 구할 수 있다. 따라서 곱셈 노드의 역전파는 상류로부터 받은 기울기에 순전파 시의 입력을 서로 바꾼 값!! 을 곱합니다.
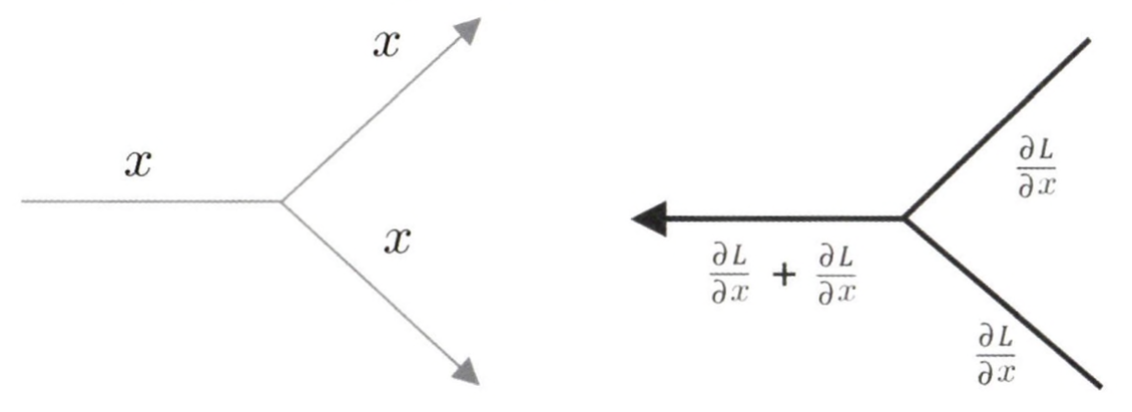
분기 노드
분기 노드는 따로 그리지 않고 단순한 선이 두 개로 나뉘도록 그리는데, 이때 같은 값이 복제되어 분기한다. 따라서 분기노드 = 복제노드 라고 할 수 있다. 그리고 그 역전파는 상류에서 온 기울기들의 합이 된다.
Repeat 노드
2개로 분기하는 노드를 일반화하면 N개로의 분기(복제)가 된다. 이를 Repeat노드라고 한다.
Repeat노드의 예를 계산 그래프로 그려보자.
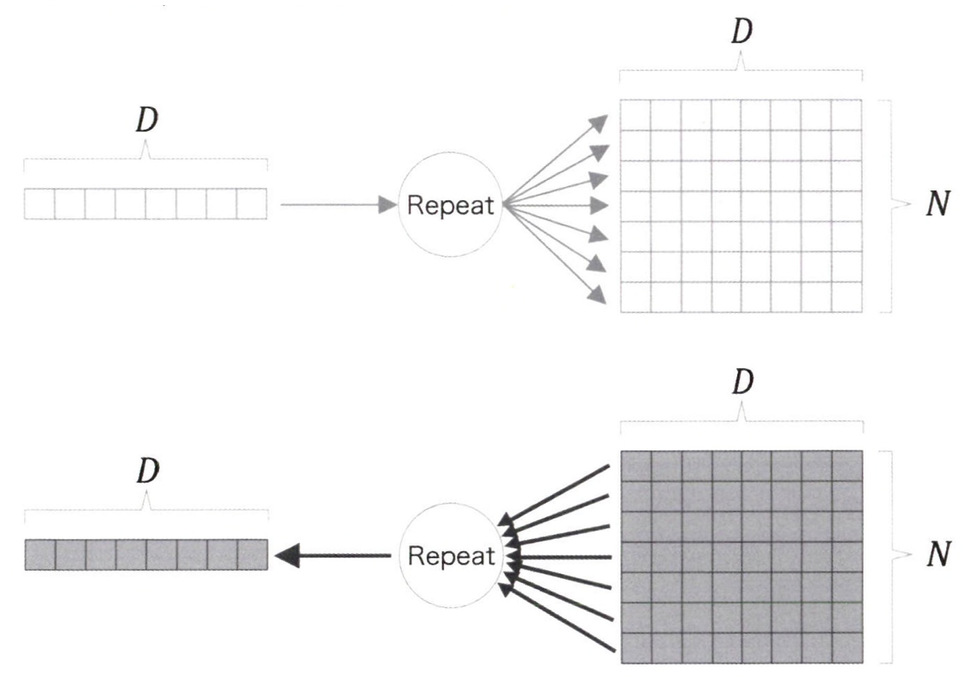
이 Repeat노드는 N개의 분기 노드로 볼 수 있으므로 N개의 기울기를 모두 더해 구할 수 있다.
import numpy as np
D, N = 8, 7
x = np.random.randn(1, D) # 입력
y = np.repeat(x, N, axis=0) # 순전파
dy = np.random.randn(N, D) # 무작위 기울기
dx = np.sum(dy, axis=0, keepdims=True) # 역전파이때 repeat() 메서드에서 axis 로 어느 축 방향으로 복제할 지 조정 가능하며, sum() 메서드에서 keepdims 속성을 True로 해주면 결과 형상은 (1, D), False로 하면 (D)가 된다.
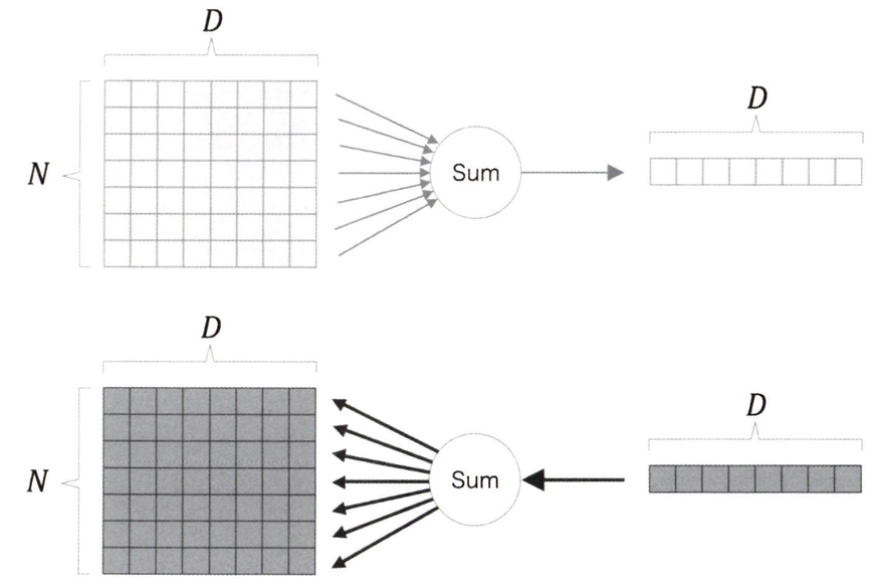
Sum노드
Sum 노드는 범용 덧셈 노드이다. 예를들어 N X D 배열에 대해 그 총합을 0축에 대해 구하는 계산을 생각해본다면 , Sum노드의 순전파와 역전파는 아래와 같이 된다.
import numpy as np
D, N = 8, 7
x = np.random.randn(N, D)
y = np.sum(x, axis=0, keepdims=True)
dy = np.random.randn(1, D)
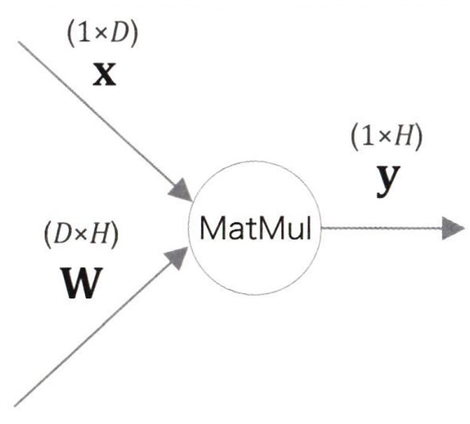
dx= np.repeat(dy, N, axis=0)MatMul 노드
x, W, y의 형상을 각각 1XD, DXH, 1XH 라고 하자.
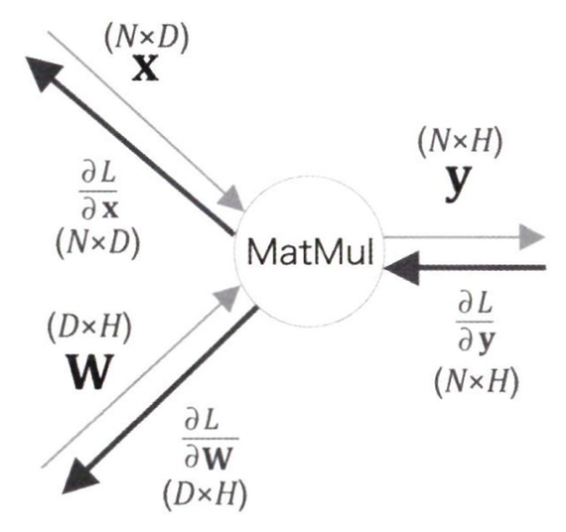
MatMul의 역전파 (x = NXD, W = DXH, y = NXH)
행렬의 형상을 확인하여 역전파 식을 유도하자.
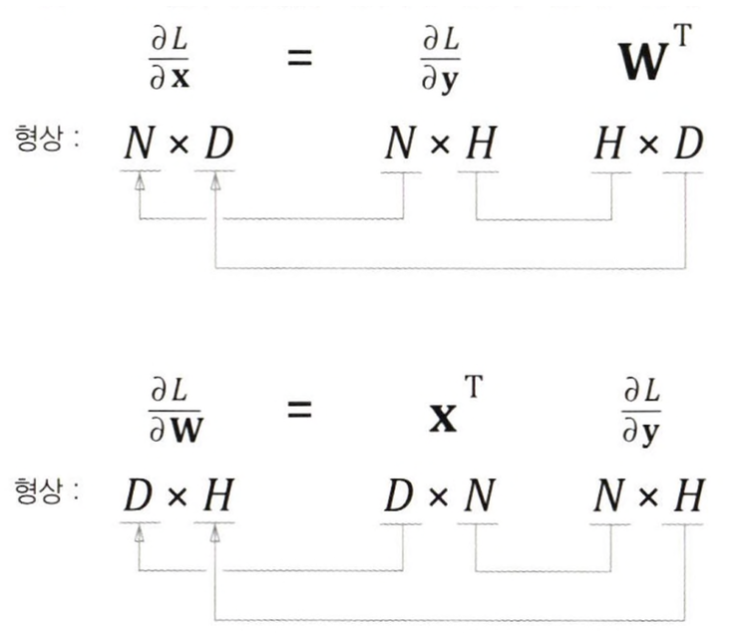
이제 행렬의 형상을 확인 후 행렬 곱의 역전파 식을 유도해 MatMul노드의 역전파까지 만들어보았으니 이 노드를 하나의 계층으로 구현해보자.
class MatMul :
def __init__ (self, W) :
self.params = [W]
self.grads = [np.zeros_like(W)]
self.x = None
def forward(self, x) :
W, = self.params
out = np.matmul(x, W)
self.x = x
return out
def backward(self, dout) :
W, = self.params
dx = np.matmul(dout, W.T)
self.grads[0][...] = dW
return dxMatMul 계층은 학습하는 매개변수를 params에 보관한다. 그리고 거기에 대응시키는 형태로, 기울기는 grads에 보관한다. 역전파에서는 dx와 dW를 구해 가중치의 기울기를 인스턴스 변수인 grads에 저장한다.
기울기 도출과 역전파 구현
Sigmoid 계층
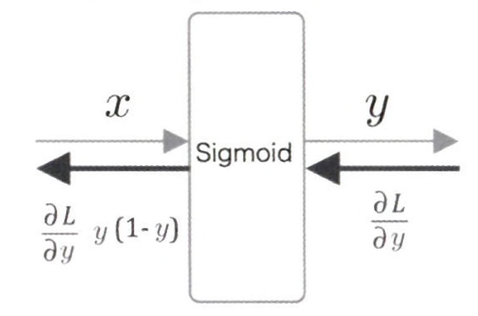
class Sigmoid :
def __init__ (self) :
self.params, self.grads = [], []
self.out = None
def forward(self, x) :
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout) :
dx = dout * (1.0 - self.out) * self.out
return dx- 순전파 때는 출력을 인스턴스 변수 out에 저장하고, 역전파를 계산할 때 이 out변수를 사용하는 모습을 볼 수 있다.
Affine 계층
앞에서와 같이 Affine 계층의 순전파는 y = np.matmul(x, W) + b 로 구현 가능하다.
여기서 편향을 더할 때는 넘파이의 브로드 캐스트가 사용된다.
이 점을 명시적으로 나타내면 Affine계층의 계산그래프는 다음과 같이 그릴 수 있다.
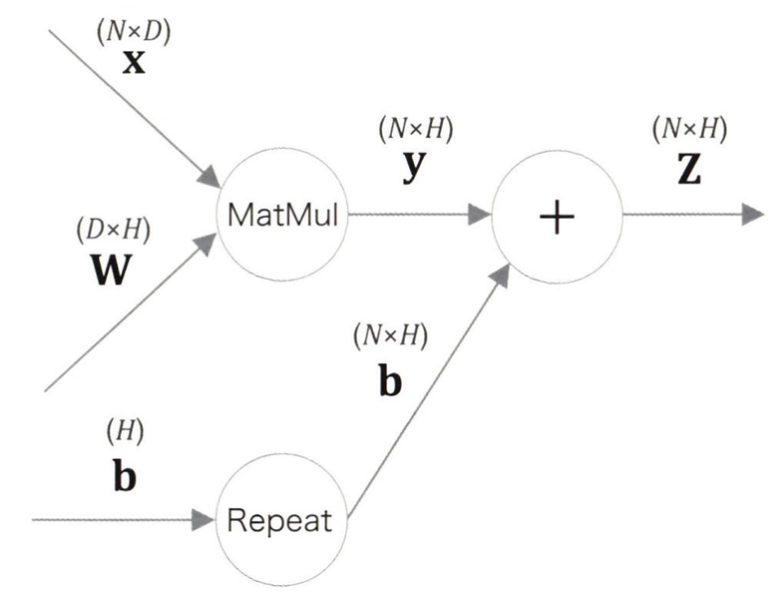
class Affine :
def __init__ (self, W, b) :
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x) :
W, b = self.params
out = np.matmul(x, W) + b
self.x = x
return out
def backward(self, dout) :
W, b = self.params
dx = np.matmul(dout, W.T)
dW = np.matmul(self.x.T, dout)
db = np.sum(dout, axis=0)
self.grads[0][...] = dW
self.grads[1][...] = db
return dxSoftmax with Loss 계층
소프트맥스 함수와 교차 엔트로피 오차는 Softmax with Loss라는 하나의 계층으로 구현한다.
아래는 이 계층의 계산 그래프이다.
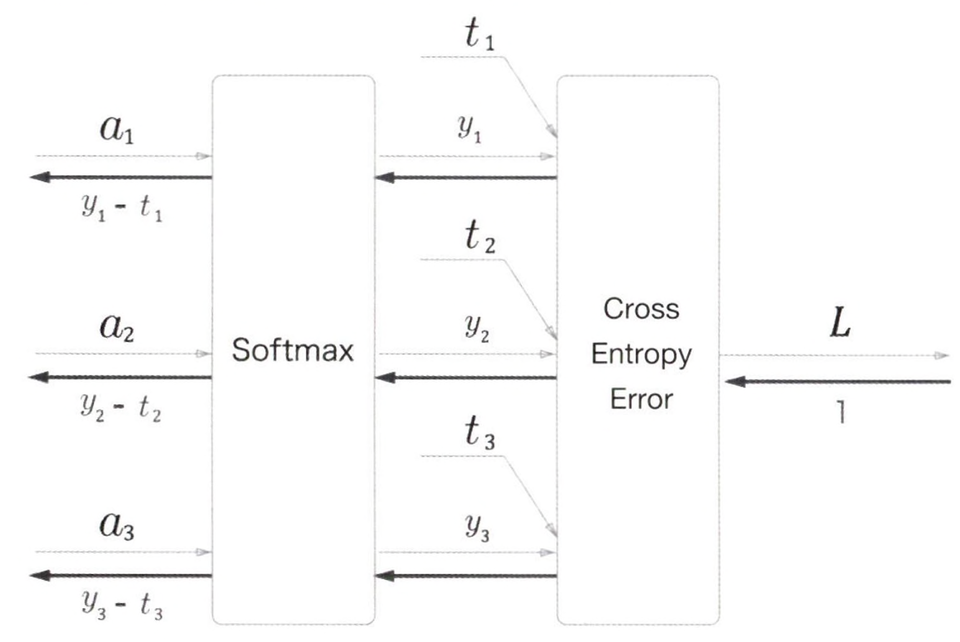
Softmax 함수 : Softmax 계층
교차 엔트로피 오차 : Cross Entropy Error 계층
→ 3-클래스 분류를 가정하여 이전 계층(입력층에 가까운 계층)으로부터 3개의 입력을 받도록 하였다.
가중치 갱신
오차역전파법으로 기울기를 구했다면, 그 기울기를 사용하여 신경망의 매개변수를 갱신한다.
이때 신경망의 학습은 다음 순서로 수행된다.

우선 미니배치에서 데이터를 선택하고, 오차역전파법으로 가중치의 기울기를 얻는다. 매개변수를 그 기울기와 반대 방향으로 갱신하며 손실을 줄인다. → 경사하강법 (Gradient Descent)
가중치 갱신 기법의 종류는 아주 다양하며 그 중 확률적 경사하강법 (SGD)을 구현해본다.
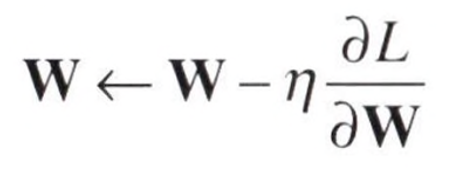
여기서 에타는 학습률(learning rate)를 나타낸다.
class SGD :
def __init__ (self, lr=0.01) :
self.lr = lr
def update(self, params, grads) :
for i in range(len(params)) :
params[i] -= self.lr * grads[i]초기화 인수 lr은 학습률을 뜻하며, 그 값을 인스턴스 변수로 저장해둔다. 그리고 update(params, grads) 메서드는 매개변수 갱신을 처리한다.
이 SGD클래스를 사용하면 신경망의 매개변수 갱신을 다음처럼 할 수 있다. (의사코드이다.)
model = TwoLayerNet(...)
optimizer = SGD()
for i in range(10000) :
...
x_batch, t_batch = get_mini_batch(...) # 미니패치 흭득
loss = model.forward(x_batch, t_batch)
model.backward()
optimizer.update(model.params, model.grads)
...이처럼 최적화를 수행하는 클래스를 분리해 구현함으로서 기능을 쉽게 모듈화 할 수 있게 했다.
