머신러닝
전통적인 프로그램은 다음과 같이 if문을 사용하여 일정 값 이상일 경우 “도미” 라고 정해진다.
if fish_length?=30 :
print("도미")but 미리 값을 정하지 못하는 경우 머신러닝을 사용한다.
도미와 빙어 데이터를 이용한 이진분류
도미와 빙어 두 클래스에 대해 이진 분류를 해보도록 하자.
분류를 위해 도미와 빙어의 데이터가 필요하다.
- 도미의 길이 , 무게 데이터
bream_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0, #길이
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0]
bream_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0, #무게
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0]- 빙어의 길이 , 무게 데이터
smelt_length = [9.8, 10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
smelt_weight = [6.7, 7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]여기서 특성 마다의 데이터 하나하나는 sample 이라고 부른다. 다른 용어로도 부르지만 , 여기서는 샘플과 특성으로 사용하도록 한다.
먼저 도미의 길이 , 무게 데이터에 대하여 그래프로 그려 파악을 해보자.
import matplotlib.pyplot as plt
plt.scatter(bream_length, bream_weight) #산점도 생성
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
xlabel 과 ylabel 을 각각 길이 , 무게로 설정하여 그래프가 그려진 모습을 확인 할 수 있다.
scatter를 두번 호출하면 한 산점도 그래프에 두개의 데이터를 중첩하여 그려주므로 빙어의 데이터도 함께 그려보자.
import matplotlib.pyplot as plt
plt.scatter(bream_length , bream_weight) #산점도 생성
plt.scatter(smelt_length , smelt_weight) #다른 데이터 삽입
plt.xlabel('length')
plt.ylabel('weight')
ply.show()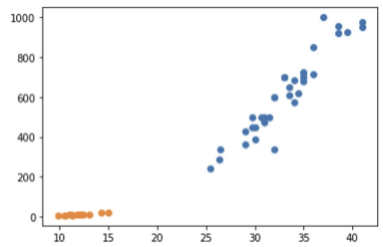
우리가 사용할 라이브러리인 scikit-learn은 데이터의 형태는 전체 생선에 대하여 길이와 무게 리스트 데이터가 들어가있는 2차원 배열을 필요로 하기에, 도미와 빙어의 length , weight 데이터를 각각 합쳐보도록 하자.
length=bream_length+smelt_length
weight=bream_weight+smelt_weight이제 length 와 weight의 데이터를 한 리스트로 합쳐야한다.
fish_data=[[l , w] for l , w in zip(length , weight)] #리스트 내포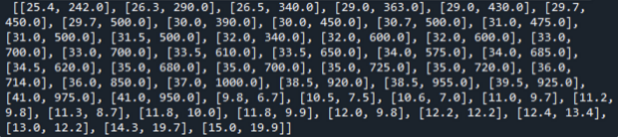
이처럼 2차원 데이터 배열이 만들어진 모습을 확인할 수 있다.
scikit-learn 은 지도학습 방식을 사용하므로 정답을 미리 준비해둔다. 이 때 정답은 target 데이터라고 부르며 , fish_data의 각 인덱스 데이터가 도미인지 , 빙어인지를 나타낸다.
target데이터는 아래와 같다.
binary classifier (이진 분류)
찾으려는 대상은 1로 , 그 외에는 0으로 표시한다.
fish_target = [1]*35 + [0]*14KNN(k-최근접 이웃 알고리즘)
- 처음 머신러닝을 접할 때 이해하기 쉽다.
scikit-learn에서 제공- 현재 포스팅에서는
fish_data,fish_target데이터를 통해 학습 진행
scikit-learn 사용
from sklearn.neighbors import KNeighborsClassifier # 라이브러리 가져오기
kn=KNeighborsClassifier(n_neighbors=49) # 인자로 주변의 가까운 데이터 몇개를 확인해볼 것인지
kn.fit(fish_data , fish_target) #머신러닝 모델 훈련 kn은 머신러닝 모델 이라고 부름
kn.score(fish_data , fish_target) #score method로 accuracy 확인이때 , KNeighborsClassifier()의 n_neighbors 인자를 조정하여 accuracy 가 변하는 모습을 볼 수 있다.
얼마나 정확한지는 알겠다 . 그렇다면 새로운 생선의 데이터가 들어왔을 때 도미인지 빙어인지 예측을 해보기 위해서는? predict 메소드를 사용한다.
kn.predict([30,600]) #어느 개체에 속하는지 알 수 있다.
array([1]) 2-1장 훈련 세트와 테스트 세트로 나누어 학습 및 평가
1)훈련 세트와 테스트 세트 나누기
1-1)샘플링 편향 방지를 위해 numpy를 이용하여 데이터 섞어 나누기
2)평가
1) 훈련 세트와 테스트 세트 나누기
numpy를 사용하여 input_arr과 target_arr 생성(numpy는 배열과 비슷하지만 다루기에 매우 편리)
import numpy as np
input_arr = np.array(fish_data)
target_arr = np.array(fish_target)
print(input_arr) 인덱스 섞기
index=np.arange(49) # 0~48 까지의 숫자를 index배열로 생성.
np.random.shuffle(index) #shuffle 함수로 섞은뒤 index 배열에 저장
train_input 데이터와 train_target 데이터 생성
train_input=input_arr[index[:35]]
train_target=target_arr[index[:35]]
test_input=input_arr[index[35:]] #테스트 데이터
test_target=target_arr[index[35:]] #테스트 데이터2) 평가
kn=kn.fit(train_input,train_target)
kn.score(test_input,test_traget)
#1.02-2장 데이터 전처리
25cm , 150g 인 생선은 도미인가 빙어인가?
1)numpy로 데이터 준비
-이전 시간까지는 리스트내포를 사용해 2차원 배열 생성 ,
train , test 데이터를 np.arange 함수를 사용하여 랜덤으로 나누어 지정
-이번 시간에는 column_stack 사용,
scikit-learn을 사용하여 데이터 나눔
fish_data=np.column_stack((fish_length , fish_weight))
fish_target=np.concatenate(np.ones(35),np.zeros(14))길이는 25cm , 무게는 150 g 인 생선의 데이터 하나를 집어넣는다.
from sklearn.model_selection import train_test_split
train_input , test_input , train_target , test_target =
train_test_split(fish_data , fish_target , stratify=fish_target , random_state=42)
#수상한 도미 데이터 넣어보기
kn=KNeighborsClassifier()
kn.fit(train_input , train_target)
kn.score(test_input , test_target)
print(kn.predict([[25,150]])
#[0,] 빙어
distances , indexes = kn.kneighbors([[25,150]]) #인접 이웃의 거리와 인덱스정보를 얻을 수 있다.
plt.scatter(train_input[:,0] , train_input[:,1])
plt.scatter(25,150,marker='^')
plt.scatter(train_input[indexes,0] , train_input[indexes,1],marker='D')
plt.xlabel('length')
plt.ylabel('weight')
ply.show() 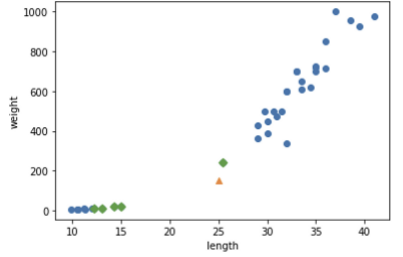
분명 길이로 따지면 도미에 훨씬 더 가까운데 왜 빙어로 구분이 될까?
▶ 무게와 길이의 기준이 서로 다르기 때문이다. 그렇기에 scale의 기준을 맞추어주어야 한다.
scale의 기준을 맞추기 위해서는 표준점수를 구하는 공식
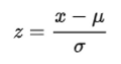
을 사용한다.
기준 변환(데이터 전처리) 방법
mean=np.mean(train_input , axis=0) #axis를 0으로 해주면 세로열에 대한 평균을 구함
std=np.std(train_input,axis=0) #표준편차 구하기
print(mean , std)
# [27.29.... 454.097 ....] [ 9.982.... 323.2989....] 평균과 표준편차 값
train_scaled = (train_input - mean) / std #train_input 의 모든 행에 대하여 mean값 -연산 수행
# -> 넘파이 브로드캐스팅
#수상한 도미 다시 표시하기
new = ([25,150] - mean)/std
plt.scatter(train_scaled[:,0],train_scaled[:,1])
plt.scatter(new[0],new[1],marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
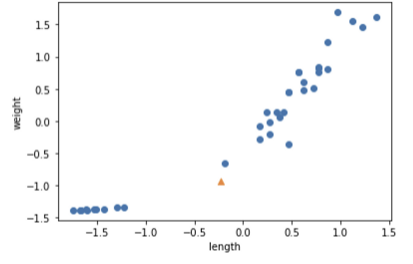
이로서 데이터의 전처리는 완료했다. x축(length)와 y축(weight) 의 값을 보면 -1.5 ~ 1.5로 통일된 상태이다.
그렇다면 전처리된 데이터에서 모델 훈련 후에 (전처리 된)수상한 도미 데이터를 넣었을 때 , 어떻게 분류되는지 보자.
#전처리 데이터에서 모델 훈련
kn.fit(train_scaled,train_target)
test_scaled=(test_input - mean ) /std #평가 데이터도 전처리를 필수로 해주자
kn.score(test_scaled,test_target) # 전처리된 평가 데이터로 평가
# 1.0 # accuracy 1.0
print(kn.predict([new]))
# [1.] -> 도미
distances , indexes=kn.kneighbors([new]) #근접 데이터 indexes 를 사용
plt.scatter(train_scaled[:,0],train_scaled[:,1])
plt.scatter(new[0],new[1],marker='^')
plt.scatter(train_scaled[indexes,0],train_scaled[indexes,1],marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()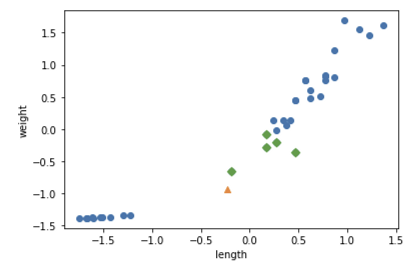
정상적으로 도미에 분류된 것으로 보인다.
다음 포스팅에서는 3장(회귀 알고리즘과 모델 규제)에 대해 다루겠다.
