[알고리즘] DFS와 BFS

1. DFS (깊이 우선 탐색, Depth-First Search)

루트 노드에서 시작하여 한 방향으로 최대한 깊숙히 들어가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 곳에서 탐색을 하는 방법이다.

Java 구현 코드

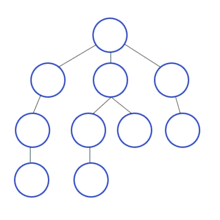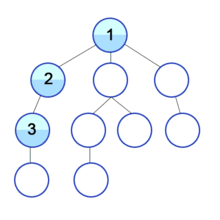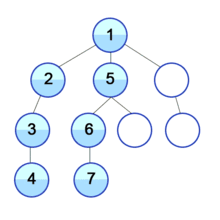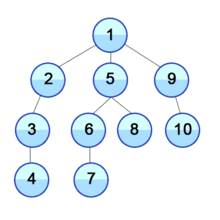
장점

1. 현 경로상의 노드들만 기억하면 되므로 저장 공간 수요가 비교적 적다.
2. 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.

단점

1. 해가 없는 경로에 깊이 빠질 가능성이 있다. 따라서 실제로 구현할 때 미리 지정한 임의 깊이까지만 탐색하고
   목표 노드를 발견하지 못하면 다음 경로를 따라 탐색하도록 하는 것이 유용하다.
2. 해를 구하면 종료되므로, 구한 해가 최단 경로가 된다는 보장이 없다.
   (목표에 이르는 경로가 다수인 경우 구한 해가 최적이 아닐 수 있음)
3. 단순 검색 속도는 BFS 보다 느리다.

시간복잡도

DFS는 그래프의 모든 간선을 조사하므로 정점의 수가 n이고 간선의 수가 e인 그래프인 경우,
그래프가 인접리스트로 표현되어 있다면 시간 복잡도가 O(n+e) 이고, 인접 행렬로 표시되어 있다면 O(n^2) 이다.

관련 문제 : 문제1 문제2

2. BFS (너비 우선 탐색, Breadth-First search)

시작 지점을 방문한 후 시작 정점에 인접한 모든 정점들을 우선 방문하는 방법이다. 더 이상 방문하지 않은 정점이 없을 때까지 방문하지 않은 모든 정점들에 대해 너비 우선 검색을 적용한다.

Java 구현 코드

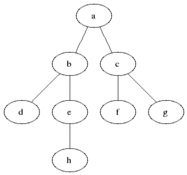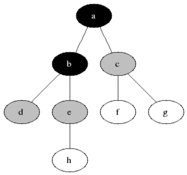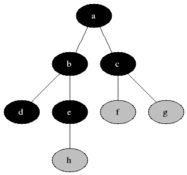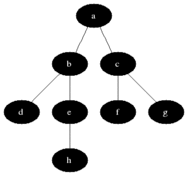
장점

1. 답이 되는 경로가 여러 개인 경우에도 최단경로임을 보장한다.
2. 최단 경로가 존재하면 깊이가 무한정 깊어진다고 해도 답을 찾을 수 있다.

단점

1. 경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간을 필요로 한다.
2. 해가 존재하지 않는다면 유한 그래프의 경우 모든 그래프를 탐색한 후 실패로 끝난다.
3. 무한 그래프의 경우에는 결코 해를 찾지 못하고, 끝내지도 못한다.

시간복잡도

DFS와 같다. 인접리스트의 경우 O(n+e), 인접행렬의 경우 O(n^2)

관련 문제 : 문제 1 문제 2

---

✔︎ DFS / BFS 차이 및 비교

• DFS는 스택(혹은 재귀), BFS는 큐를 사용한다.
• BFS는 재귀적으로 동작하지 않는다.

문제 푸는 입장에서 비교

• 최단 거리 문제를 푼다면 BFS를 사용한다.
• 이동할 때마다 가중치가 붙어서 이동한다거나 이동 과정에서 여러 제약이 있을 경우 DFS로 구현하는 것이 좋다.
  DFS /BFS 문제 추천

이미 출처 - 위키 백과