data_structure
1.트리의 개념과 이진 트리
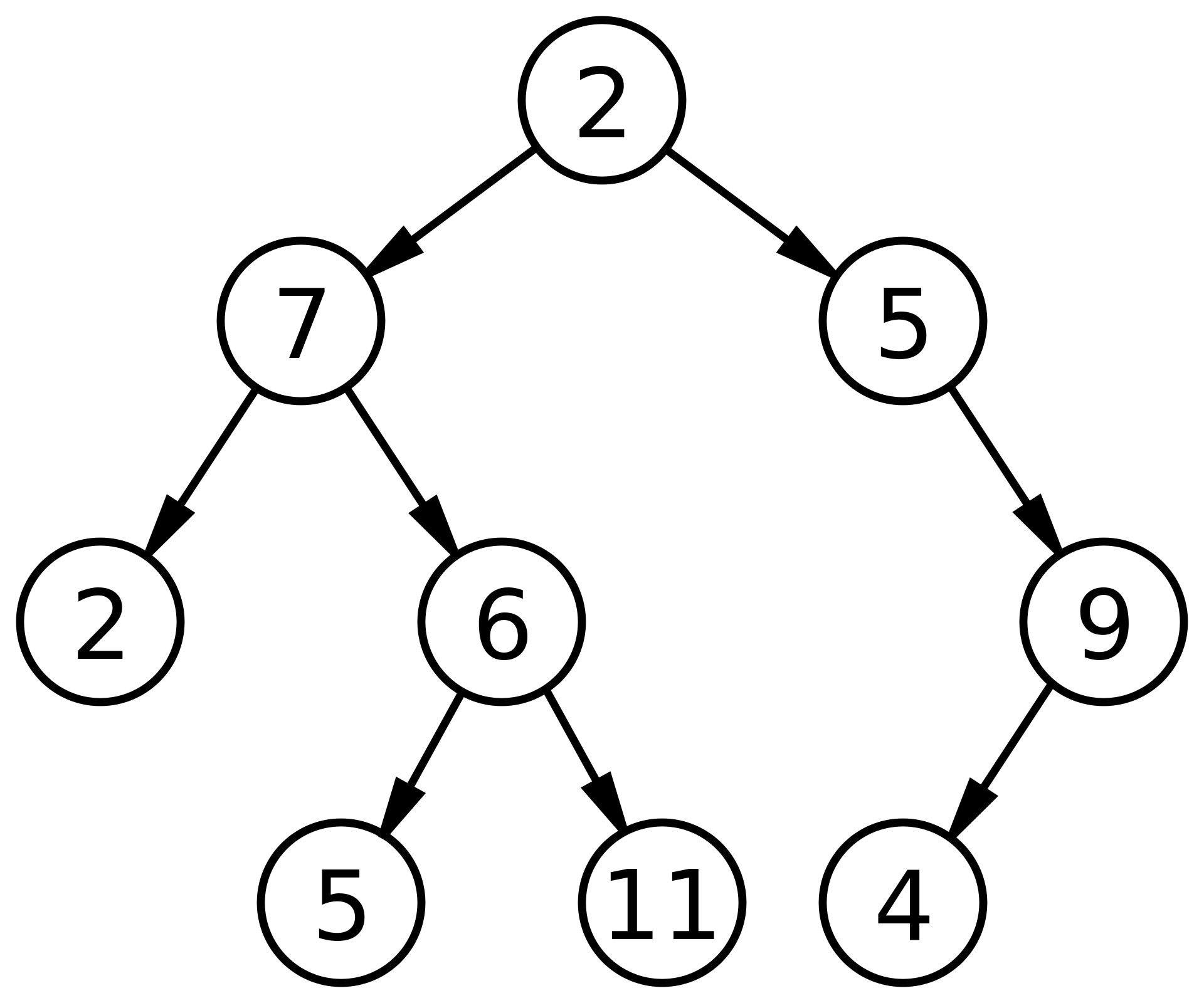
트리(Tree)란, 배열, 링크드리스트, 스택, 큐와 같이 일직선 개념의 자료구조가 아니라 부모-자식 개념을 가지는 자료구조이다.(출처 : 위키피디아)트리는 위 그림처럼 표현이 되는 자료구조인데, 여기서 원으로 표시되는 2, 7, 5 등을 노드라고 하고 2는 7과 5의
2.이진 트리 구현 배열 vs 리스트

이 페이지(https://stackoverflow.com/questions/29225391/binary-trees-arrays-vs-linked/292256701\. 자식 노드를 찾는 게 빠르다. 이 말은 곧, 왼쪽 자식 노드 값을 알기 위해서는 arr2k
3.배열을 이용한 이진 트리 구현

이 페이지를 참고하여 정리하였습니다.위와 같은 트리가 있다고 할 때, 배열을 이용하여 구현하면 아래와 같이 각각 노드에 인덱스를 부여할 수 있습니다.B 인덱스(1) = A 인덱스(0) 2 + 1C 인덱스(2) = A 인덱스(0) 2 + 2D 인덱스(3) = B 인덱
4.리스트를 이용한 이진 트리 구현

이 페이지를 참고하여 정리하였습니다.위와 같은 트리가 있다고 할 때, 리스트를 이용하여 구현한다고 하면 하나의 Node는 자신의 왼쪽과 오른쪽에 어떤 노드가 오는지(어떤 자식 노드가 오는지) 알고 있어야 합니다.만약 C를 이용하여 이를 구현한다 하면 Node 구조체를
5.이진 탐색 트리(Binary Search Tree) 구현 - 기본 개념 및 삽입
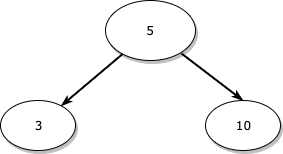
구현에 대한 전체 코드는 이곳에서 확인할 수 있습니다.먼저, 구현할 이진 탐색 트리는 아래와 같은 형태로 되어 있습니다.자기 자신보다 왼쪽에는 값이 작은 노드가, 오른쪽에는 값이 큰 노드가 와야 한다는 이진 탐색 트리의 조건으로 인해 3은 5보다 왼쪽에, 11은 10보
6.이진 탐색 트리(Binary Search Tree) 구현 - 삭제
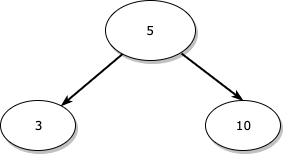
이진 탐색 트리(Binary Search Tree) 구현 - 기본 개념 및 삽입 글을 먼저 읽고 오시면 이 글을 이해하는데 더욱 좋을 것 같습니다.구현에 대한 전체 코드는 이곳에서 확인할 수 있습니다.삭제는 삽입과 다르게 되게 많은 케이스를 생각해야 합니다.제가 정리한
7.그래프(Graph)란?
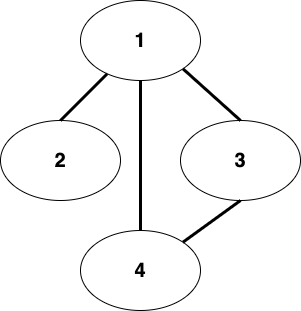
그래프의 정의를 하나의 문장을 딱 내리기에는 애매하니, 제 성격상 그냥 트리에서 좀 더 발전한 자료구조라고만 하겠습니다.어차피, 정의를 달달 외우고 다니는 것보다, 실제 특징들을 제대로 설명할 수 있는 게 더 중요하니깐요.바로 아래 내용들을 보면서 어떤 개념들을 가지고
8.그래프(Graph) BFS의 개념과 구현
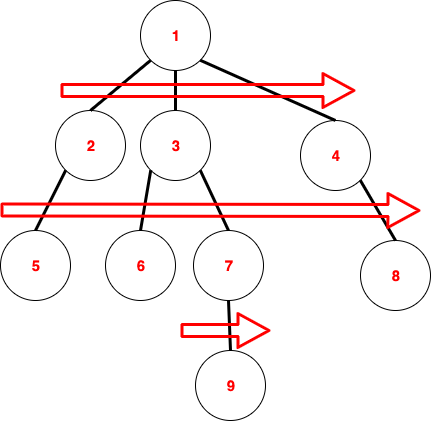
이전 글인 그래프(Graph) DFS의 개념과 구현에 이어서 작성하는 글입니다.이번 글은 BFS(Breadth-First Search, 너비 우선 탐색)에 대해 알아보겠습니다.너비 우선 탐색은 말 그대로 너비를 우선으로 하여 탐색하는 방법입니다.아래 그림을 통해 이해하
9.그래프(Graph) DFS의 개념과 구현
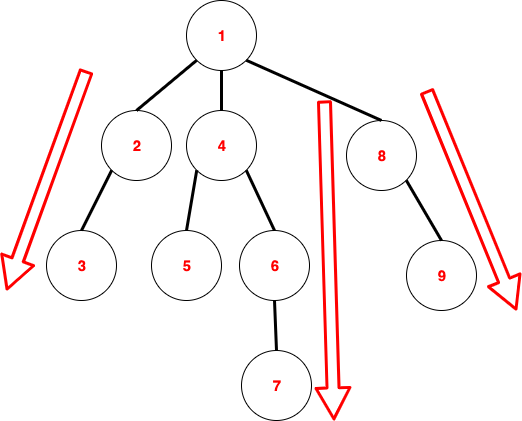
그래프의 순회 방법에는 DFS, BFS가 있습니다.그 중 먼저 DFS(Depth-First Search, 깊이 우선 탐색)에 대해 알아보겠습니다.깊이 우선 탐색은 말 그대로 깊이를 우선으로 하여 탐색하는 방법입니다.아래 그림을 통해 이해하는 것이 쉬울 것 같습니다.(노