세그먼트 트리

참고: 백준 사이트 설명

동기

$A = [a_1, a_2, ..., a_N]$ 배열이 주어졌을 때 다음 두 가지 연산을 효율적으로 풀기 위한 알고리즘이다.

1. $a_i$부터 $a_{i + j}$까지의 구간합을 구하는 연산
2. $a_k$의 값을 바꾸는 연산

위 연산이 모두 $K$번 있다고 하자.

구간합 연산만 있을 경우 일반적인 누적합을 사용하면 $O(N)$ 연산 한 번 수행하면 나머지는 $O(1)$이므로 전체 시간 복잡도는 $O(N + K)$이다.
문제는 2번 연산인데, 중간의 값을 바꿀 때마다 구간합을 새로 구해야 하므로 $O(N)$의 연산을 다시 해야 한다. 따라서 $O(N * K)$의 시간복잡도가 나오므로 다른 방법으로 풀어야 한다.

구조

배열을 다음과 같은 바이너리 트리 구조로 바꿔 사용한다. 트리를 사용하면 메모리를 더 사용하지만 구조상 대부분의 연산이 $O(\log{N})$의 시간복잡도를 가지게 되는 장점이 있으므로 사용하는 것이다.

• 리프 노드: 배열의 원소

  배열의 원소가 $N$개이므로 필요한 전체 노드의 수는 $2^{int(\log{N}) + 2}-1$이다. 코드 구현에는 순회를 편하기 하기 위해 루트 노드의 인덱스를 1로 하므로 길이가 $2^{int(\log{N}) + 2}$인 배열을 사용한다.

• 다른 노드: 왼쪽 자식과 오른쪽 자식의 합

예를 들어 10개의 원소를 가진 배열은 다음과 같은 트리가 된다.

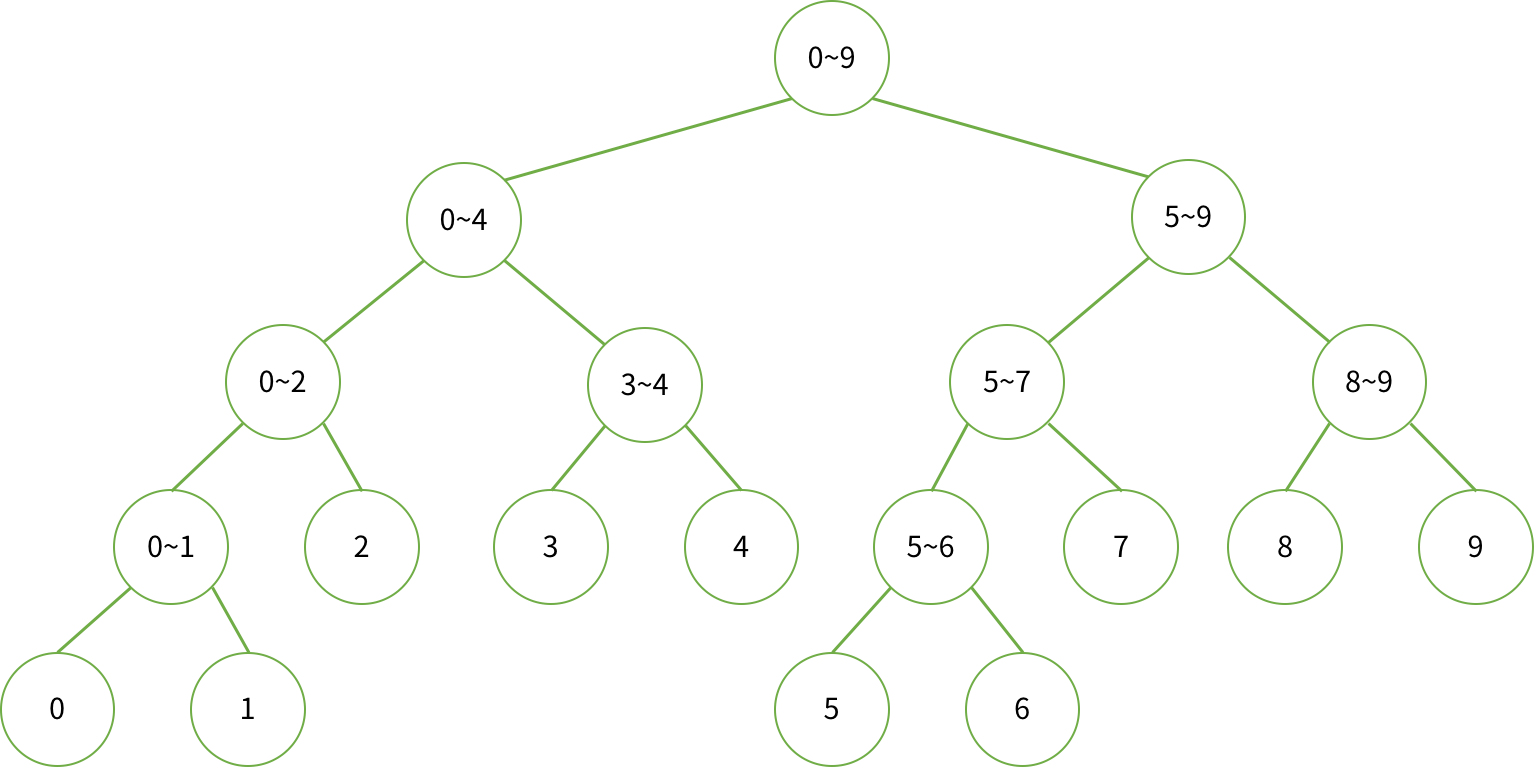
코드

다른 코드도 마찬가지지만, 트리 구조를 사용하므로 재귀를 사용한다.

import math


class SegmentTree:
    def __init__(self, arr):
        self.arr = arr
        self.tree_len = 2 ** (int(math.log(self.arr_len, 2)) + 2)
        self.tree = [0] * self.tree_len
        self._create_tree(0, len(arr) - 1)

    def _create_tree(self, start: int, end: int, idx: int = 1):
        if start == end:
            self.tree[idx] = self.arr[start]
            return
        self._create_tree(start, (start + end) // 2, idx * 2)
        self._create_tree((start + end) // 2 + 1, end, idx * 2 + 1)
        self.tree[idx] = self.tree[idx * 2] + self.tree[idx * 2 + 1]

구간합

이분 탐색의 형식으로 구간합을 구하게 되므로 $O(\log{N})$의 시간 복잡도를 가지게 된다.

예를 들어 2번째 원소부터 4번째 원소까지의 합을 구한다고 하면 다음과 같은 값들을 참조하면 된다.

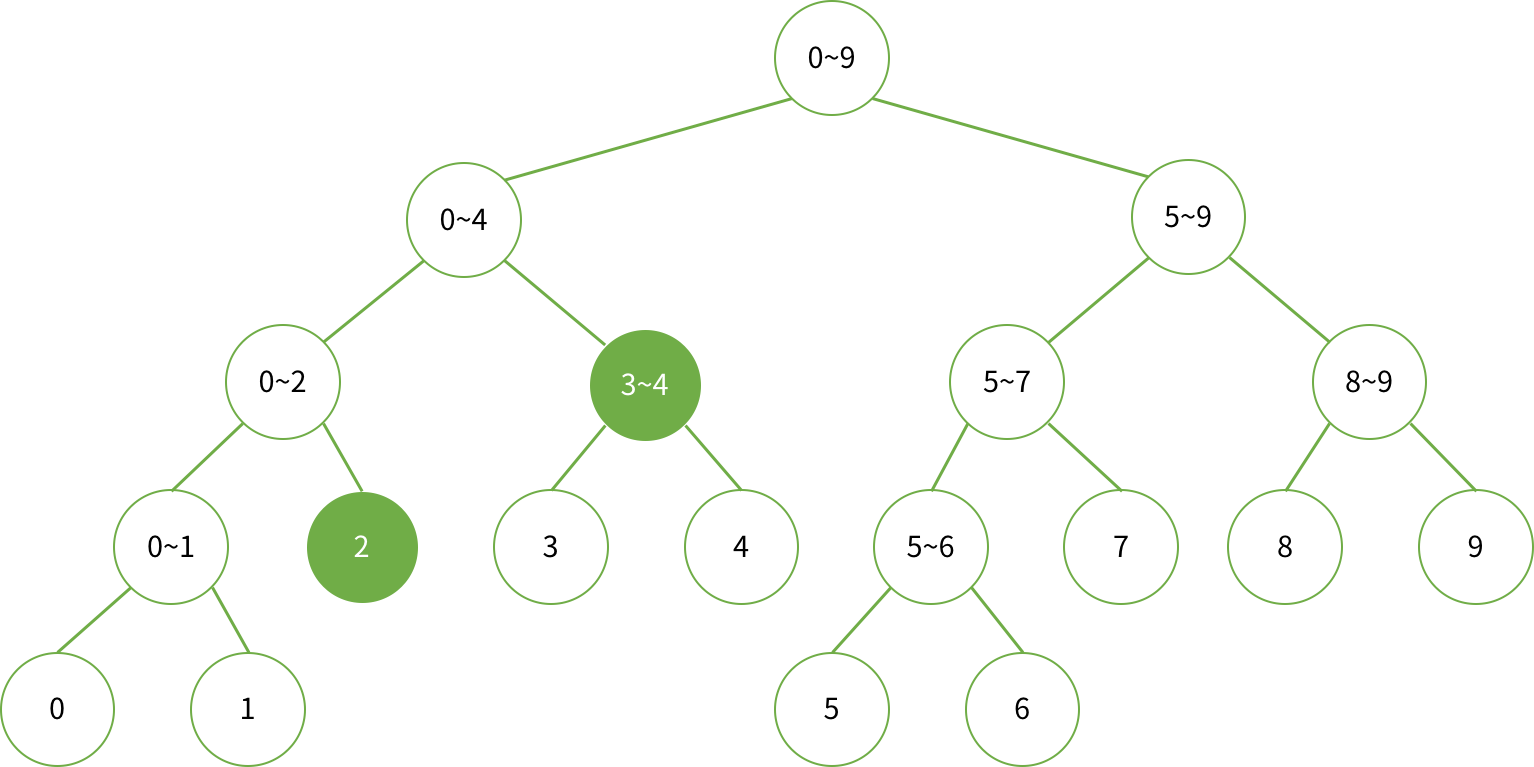
다른 예로 3번째부터 9번째는 다음과 같다.

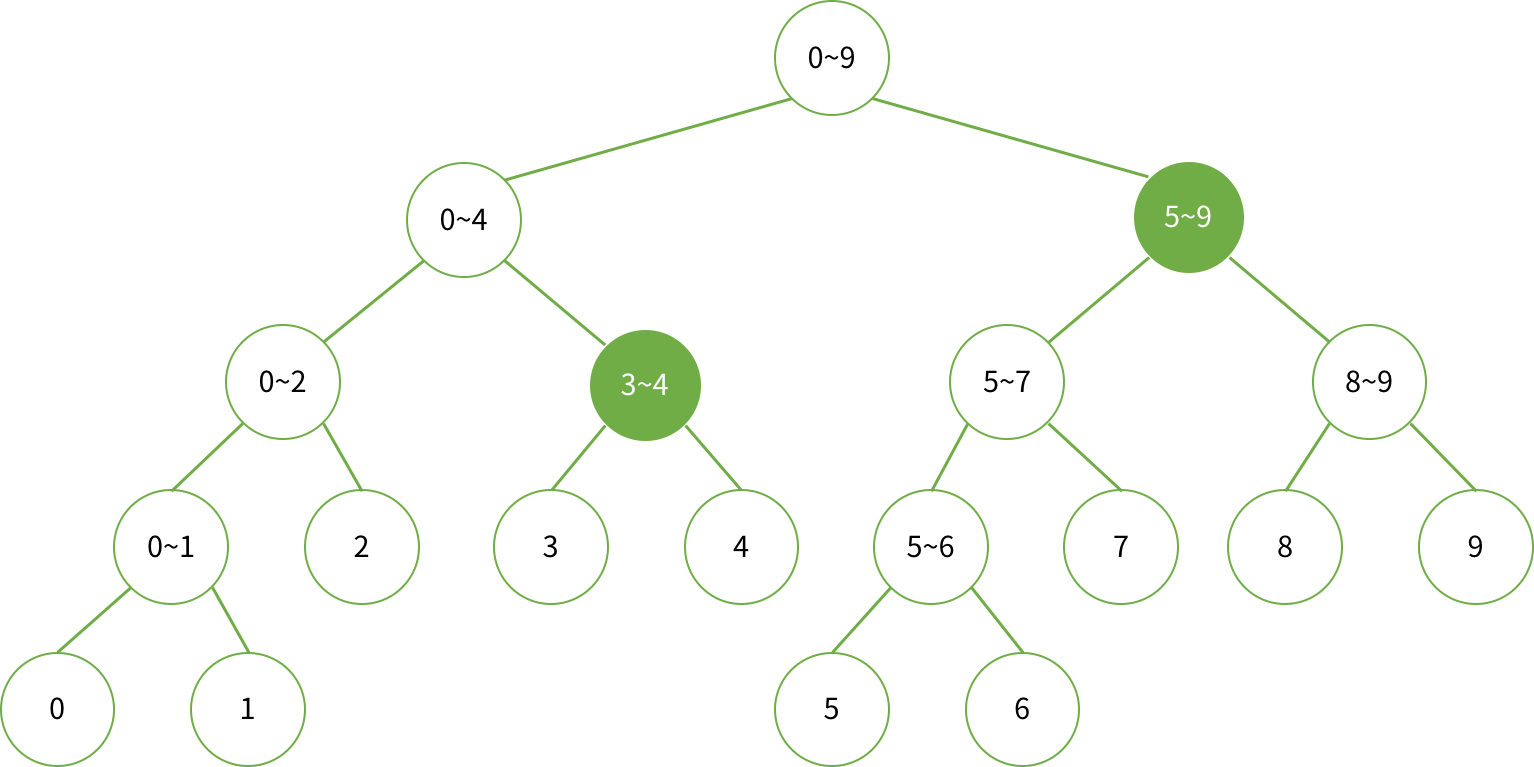
코드

class SegmentTree:
    ...
    def get_sub_sum(self, left, right):
        return self._get_sub_sum(0, self.arr_len - 1, left, right)

    def _get_sub_sum(self, start, end, left, right, idx=1):
        '''
        start, end: value for tree
        left, right: value for arr
        idx: tree index
        '''
        if end < left or right < start:
            return 0
        if left <= start and end <= right:
            return self.tree[idx]
        return self._get_sub_sum(start, (start + end) // 2, left, right, idx * 2) + self._get_sub_sum(
            (start + end) // 2 + 1, end, left, right, idx * 2 + 1)

원소 교체

특정 값을 바꾸는 경우 그 값과 관련있는 노드들을 전부 바꿔줘야 한다. 이 경우에도 이분 탐색의 형식으로 바꾸면 되므로 $O(\log{N})$의 시간복잡도를 가진다.

예를 들어 인덱스 3의 원소를 바꾸면 다음 노드들을 업데이트해야 한다.

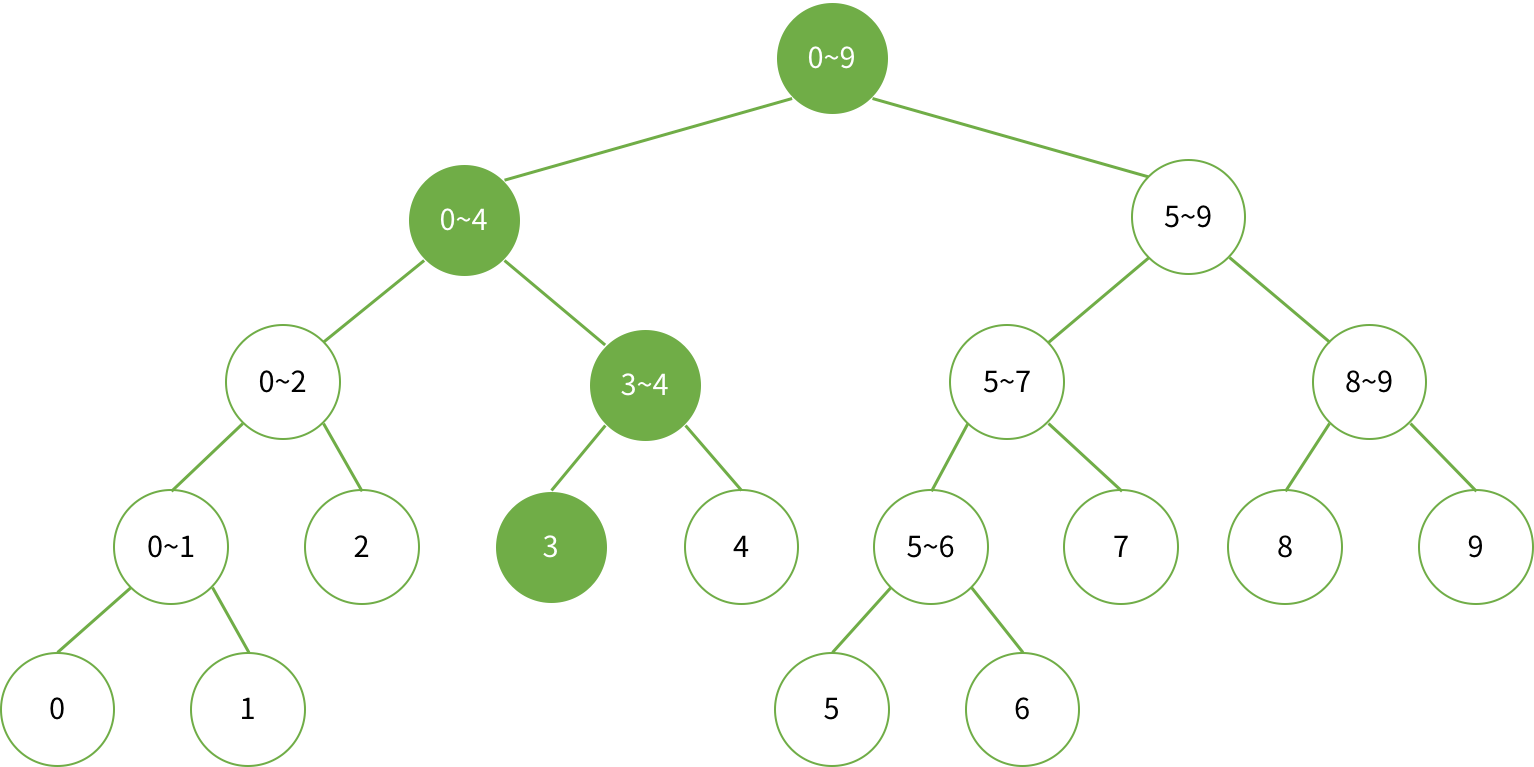
다른 예로 5의 원소를 바꾸면 다음 노드들을 업데이트해야 한다.

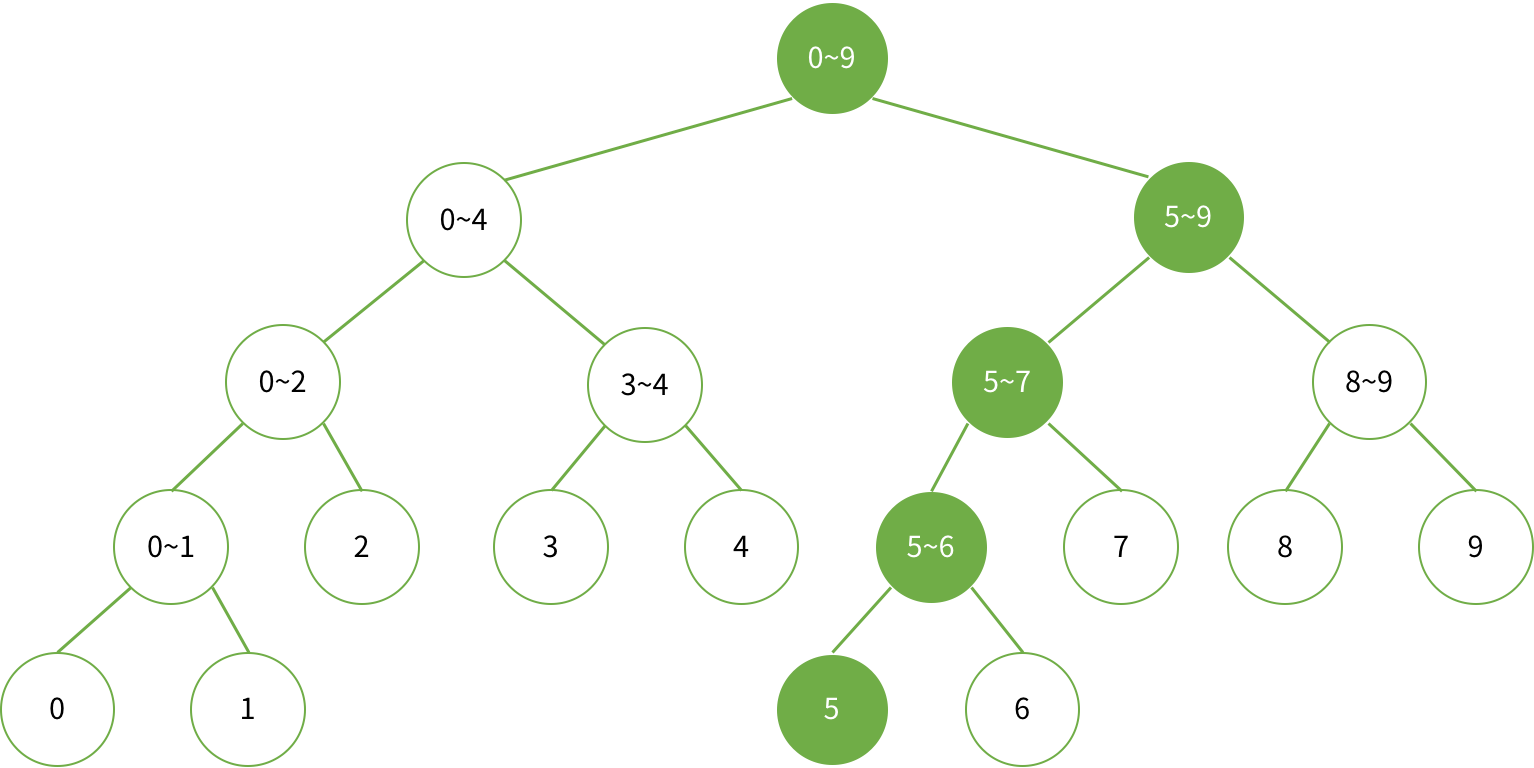
코드

class SegmentTree:
	...
    def change_num(self, val, arr_idx):
        self._change_num(val, arr_idx, 0, self.arr_len - 1)
        self.arr[arr_idx] = val

    def _change_num(self, val, arr_idx, start, end, idx=1):
        if start == end:
            if start == arr_idx:
                self.tree[idx] = val
            return
        if start <= arr_idx <= end:
            self.tree[idx] -= self.arr[arr_idx]
            self.tree[idx] += val
            self._change_num(val, arr_idx, start, (start + end) // 2, idx * 2)
            self._change_num(val, arr_idx, (start + end) // 2 + 1, end, idx * 2 + 1)
        return

전체 코드

class SegmentTree:
    def __init__(self, arr):
        self.arr = arr
        self.arr_len = len(arr)
        self.tree_len = 2 ** (int(math.log(self.arr_len, 2)) + 2)
        self.tree = [0] * self.tree_len
        self._create_tree(0, len(arr) - 1)

    def _create_tree(self, start: int, end: int, idx: int = 1):
        if start == end:
            self.tree[idx] = self.arr[start]
            return
        self._create_tree(start, (start + end) // 2, idx * 2)
        self._create_tree((start + end) // 2 + 1, end, idx * 2 + 1)
        self.tree[idx] = self.tree[idx * 2] + self.tree[idx * 2 + 1]

    def get_sub_sum(self, left, right):
        return self._get_sub_sum(0, self.arr_len - 1, left, right)

    def _get_sub_sum(self, start, end, left, right, idx=1):
        '''
        start, end: value for tree
        left, right: value for arr
        idx: tree index
        '''
        if end < left or right < start:
            return 0
        if left <= start and end <= right:
            return self.tree[idx]
        return self._get_sub_sum(start, (start + end) // 2, left, right, idx * 2) + self._get_sub_sum(
            (start + end) // 2 + 1, end, left, right, idx * 2 + 1)

    def change_num(self, val, arr_idx):
        self._change_num(val, arr_idx, 0, self.arr_len - 1)
        self.arr[arr_idx] = val

    def _change_num(self, val, arr_idx, start, end, idx=1):
        if start == end:
            if start == arr_idx:
                self.tree[idx] = val
            return
        if start <= arr_idx <= end:
            self.tree[idx] -= self.arr[arr_idx]
            self.tree[idx] += val
            self._change_num(val, arr_idx, start, (start + end) // 2, idx * 2)
            self._change_num(val, arr_idx, (start + end) // 2 + 1, end, idx * 2 + 1)
        return