Backpropagation

reference : https://cs231n.github.io/optimization-2/ - 2022/11/12

dot연산의 scores function으로 각 클래스 마다의 점수를 구하고, 이를 사용해 SVM이나 softmax와 같은 손실함수를 통해 loss를 구한다. 이에 regularization을 더해 총 loss를 구한다. 이 loss를 작게 만들기 위해 W를 조정한다. 산의 경사를 따라 내려간다는 것 처럼 loss가 감소하는 방향으로 분류기를 수정한다. 이를 optimization이라 한다. 이때, numerical, analytic과 같은 방식으로 optimization을 한다.

Backpropagation은 네트워크 전체에 대해 반복적인 연쇄 법칙(Chain rule)을 적용하여 Gradient를 계산하는 방법 중 하나이다. 이는 신경망을 효과적으로 개발하고 디자인하고 디버그하는데 중요하다. score를 구하는 것부터 regulariztion을 거쳐 loss를 구하는 것을 한줄로 늘어뜨려 구하는 것은 꽤나 큰 scale로 연산이 오래 걸린다. 그래서 간단한 학습 방법을 알고자 한다.

핵심 Probelm: 주어진 함수 $f(x)$ 가 있고, $x$ 는 입력 값으로 이루어진 벡터이고, 주어진 입력 $x$ 에 대해 함수 $f$ 의 그라디언트를 계산하고자 한다.

$f(x)$ 는 손실함수 ($L$)에 해당하고 입력 값 $x$ 는 학습 데이터(Training data)와 신경망의 Weight라고 볼 수 있다. 예를 들면, 손실함수는 SVM Loss 함수가 될 수 있고, 입력 값은 학습 데이터($x_i, y_i), i = 1,2,...,N$)와 Weight, bias 로 볼 수 있다. 여기서 학습 데이터는 미리 주어져서 고정 되어있는 값으로 볼 수 있고, Wsight는 신경망 학습을 위해 실제로 컨트롤 하는 값이다. 따라서 입력 값 $x_i$ 에 대한 그라디언트 계산이 쉬울지라도, 실제로는 파라미터(Parameter) 값에 대한 그라디언트를 일반적으로 계산하고, 그라디언트 값을 활용하여 파라미터를 업데이트 할 수 있다. (입력 값 $x_i$ 에 대한 그라디언트는 신경망 작동 해석과 시각화 하는 부분에서 활용될 수 있다)

Gradient에 대한 간단한 표현과 이해

아래의 사진은 함수 f와 편미분이다.

미분은 입력 변수 부근의 아주 작은 변화에 대한 함수 값의 변화량이다.

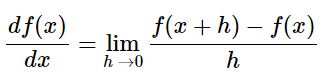
즉, 미분은 각 변수가 해당 값에서 전체 함수의 결과 값의 영향을 미치는 민감도와 같은 개념이다. 그라디언트 $∇f$ 는 편미분 값들의 벡터이다. 따라서 수식으로 표현하면 $∇f=[∂f/∂x,∂f/∂y]=[y,x]$, 그라디언트가 벡터일지라고 심플한 표현을 위해 "X에 대한 편미분"이라는 정확한 표현 대신 "X에 대한 그라디언트"라는 표현을 종종 쓰게 될 예정이다.

연쇄 법칙(Chain rule)을 이용햔 복합 표현식

이제 f(x,y,z)=(x+y)z 같은 다수의 복합 함수(composed functions)를 수반하는 더 복잡한 표현식을 고려해보자. 이 식은 $q=x+y$ 와 $f=qz$ 으로 분해될 수 있다.

• $∂f/∂q=z$, $∂f/∂z=q$
• $∂q/∂x=1$, $∂q/∂y=1$

이고, 궁극적으로 우리는 $x, y, z$ 에 대한 $f$ 의 그라디언트에 관심이 있다. 연쇄법칙은 이러한 그라디언트 표현식들을 연결시키는 방법이 곱이라는 것을 보여준다.
$∂f/∂x=∂f/∂q*∂q/∂x$ 로 표현할 수 있다.

# set some inputs
x = -2; y = 5; z = -4

# perform the forward pass
q = x + y # q becomes 3
f = q * z # f becomes -12

# perform the backward pass (backpropagation) in reverse order:
# first backprop through f = q * z
dfdz = q # df/dz = q, so gradient on z becomes 3
dfdq = z # df/dq = z, so gradient on q becomes -4
# now backprop through q = x + y
dfdx = 1.0 * dfdq # dq/dx = 1. And the multiplication here is the chain rule!
dfdy = 1.0 * dfdq # dq/dy = 1

결국 $[df/dx, df/dy, df/dz]$ 변수들로 그라디언트가 표현되는데, 이는 f에 대한 변수 x,y,z의 민감도(sensitivity)를 보여준다. 더 나아가서 보다 간결한 표기법을 사용해서 df 파트를 계속 쓸 필요가 없도록 하고 싶을 것이다. 예를 들어 dfdq 대신에 단순히 dq를 쓰고 항상 그라디언트가 최종 출력에 관한 것이라 가정하는 것이다.

또한 계산을 회로도를 가지고 시각화할 수 있다.

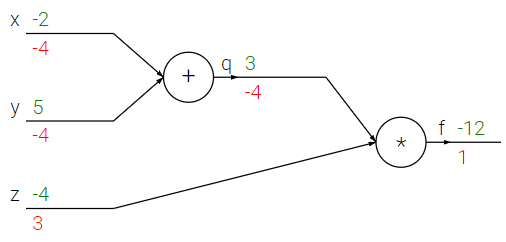
전방 전달(forward pass)은 입력부터 출력까지 값을 계산한다 (녹색으로 표시). 그리고 나서 후방 전달(backward pass)은 backpropagation을 수행하는데, 이는 끝에서 시작해서 반복적으로 연쇄 법칙을 적용해 회로 입력에 대한 모든 길에서 그라디언트 값(적색으로 표시)을 계산한다. 그라디언트 값은 회로를 통해 거꾸로 흐르는 것으로 볼 수 있다.

Backpropagation에 대한 직관적 이해

backpropagation이 굉장히 지역적인 프로세스임에 주목하자. 회로도 내의 모든 게이트(gate) 몇 개의 입력을 받아들이고 (Forward Pass 시)곧 바로 두 가지를 계산할 수 있다.

1. 게이트의 출력값
2. 게이트 출력에 대한 입력들의 Local Gradient 값 저장 (e.g. $∂q/∂x=1$, $∂q/∂y=1$) (add gate > 1, multipky gate > 반대 입력 값)

일단 전방 전달(Forward Pass)이 끝나면 backpropagation 과정에서 게이트는 결국 전체 회로의 마지막 출력에 대한 게이트 출력의 그라디언트 값(Global Gradient)에 관해 학습할 것이다.(역으로 내려와서 전달 받은 그라디언트 값) 연쇄 법칙을 통해 게이트는 이 그라디언트 값(Global Gradient)을 받아들여 모든 입력에 대해서 계산한 게이트의 모든 그라디언트 값(Local Gradient)에 곱한다. 따라서 입력값 x, y, z에 대한 f 즉, loss function의 최종 미분 값을 얻을 수 있게 된다.

• 연쇄 법칙 덕분에 역으로 내려온 Global Gradient 값과 Foward Pass 과정에서 저장한 Local Gradient 값을 곱함으로 최종 Gradient를 구하기 때문에 신경망 같은 복잡한 회로에서 각각의 게이트의 중요도를 낮춰 계산을 간단히 할 수 있다.

backpropagation은 보다 큰 최종 출력 값(더 나은 값)을 얻도록 게이트들이 자신들의 출력이 (얼마나 강하게) 증가하길 원하는지 또는 감소하길 원하는지 서로 소통하는 것으로 간주할 수 있다.

Modularity: Sigmoid example

어떤 종류의 함수도 미분가능하다면 게이트(함수, layer)로서 역할할 수 있다. 실제적으로 좀 더 복잡한 예를 알아보자.

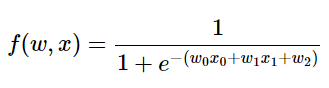
위의 표현식은 시그모이드 활성함수를 사용하는 2차원 뉴런(x, W를 갖는다)을 나타낸다.

먼저 간단한 미분을 먼저 해 놓자.

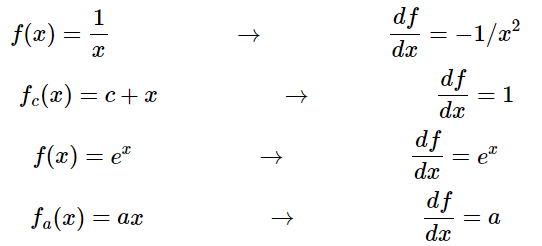
코드로 나타내면,

w = [2,-3,-3] # assume some random weights and data
x = [-1, -2]

# forward pass
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid function

# backward pass through the neuron (backpropagation)
ddot = (1 - f) * f # gradient on dot variable, using the sigmoid gradient derivation
dx = [w[0] * ddot, w[1] * ddot] # backprop into x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # backprop into w
# we're done! we have the gradients on the inputs to the circuit

• Tip: 위 코드에서 볼 수 있듯이, 전방 전달(forward pass)를 쉽게 backprop되는 단계들로 잘게 분해하는 것은 실질적으로 항상 도움이 된다. (e.g. sigmoid function) 예를 들어 우리는 여기서 w와 x 사이의 내적의 결과를 담는 중간 변수 dot를 만들었다. 그리고나서 후방 전달(backward pass) 과정에서 그러한 변수들의 그라디언트 값들을 담은 해당 변수들(예: ddot 및 궁극적으로는 dw, dx)을 성공적으로 계산한다

회로도로 나타내면, 이렇게 나오게 된다.

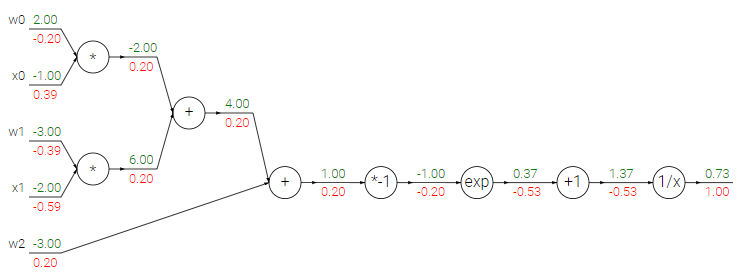
위의 예에서 w,x 사이의 내적의 결과($w_0 * x_0 + w_1 * x_1 + w_2$)로 동작하는 함수의 긴 체인을 보았다.

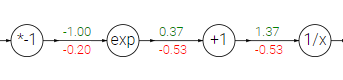
이러한 연산을 제공하는 함수를 시그모이드 함수(sigmoid function) σ(x)라고 한다. 사그모이드 함수는 미분을 자기 자신으로 간략화할 수 있는 특성을 갖고 있다.

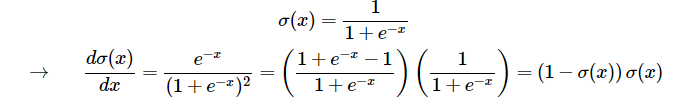
이 특성을 활용하면계산 과정이 간단해진다.

이 긴 체인을 sigmoid gate라 하고 Forward pass 과정에서 입력 1.0을 받아 출력 0.73을 계산한다. backpropagation 과정에서 Local gradient는 $(0.73) * (1 - 0.73) = 0.2$ 라는 시그모이드함수의 미분 함수로 간단하게 구하고 Global gradient 0.1과 곱해 gradient를 0.2 로 간단히 구할 수 있다.

• gate 별 특성 (연산을 쉽게 하기 위해 외우는게 좋음)

1. add gate: gradient distributor로 전의 gradient를 그대로 전파함(Local gradient가 모두 1임)
2. mul gate: Local gradient가 반대 입력 값이 되기 때문에 "switcher"..?
3. max gate: 큰 입력값의 Local gradient는 1 작은 입력값의 Local gradient는 0이 되므로, 여러 개 중 하나만 취해준다라는 뜻의 "gradient router"

• Gradients add at branches (Backpropagation 과정 중 뒷 단이 여러 개로 분기되는 경우)
  그냥 더 해준다.

실제 backprop 단계적 계산

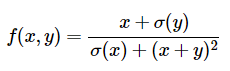
위 함수를 가정하자. 우리는 위 함수를 미분한 함수를 알 필요 없다. 그저 그라디언트를 어떻게 계산하고 값을 얻을 수 있으면 된다.

먼저 전방 전달을 구조화 하는지를 나타낸 것이다.

x = 3 # example values
y = -4

# forward pass
sigy = 1.0 / (1 + math.exp(-y)) # sigmoid in numerator   #(1)
num = x + sigy # numerator                               #(2)
sigx = 1.0 / (1 + math.exp(-x)) # sigmoid in denominator #(3)
xpy = x + y                                              #(4)
xpysqr = xpy**2                                          #(5)
den = sigx + xpysqr # denominator                        #(6)
invden = 1.0 / den                                       #(7)
f = num * invden # done!                                 #(8)

각각이 단순한 표현식들인 다수의 중간 변수들을 포함하는 방식으로 코드를 구조화한 것에 주목하자, 우리는 이미 이 표현식들에 대한 지역 그라디언트 값을 알고 있다.(전방 전달에 미리 저장하기 때문) 그러므로, backprop 전달을 계산하는 것은 쉬운 일이다

전방 전달 과정의 모든 변수들(sigy, num, sigx, xpy, xpysqr, den, invden)에 대해 역방향으로 가면서 똑같은 변수들을 볼 것이다, 다만 해당 변수에 대한 회로 출력의 그라디언트를 담는 것을 나타내기 위해 변수명 앞에 d를 붙인다.

# backprop f = num * invden
dnum = invden # gradient on num (mul gate)                        #(8)
dinvden = num (mul gate)                                          #(8)
# backprop invden = 1.0 / den
dden = (-1.0 / (den**2)) * dinvden # Lg * Gg                      #(7)
# backprop den = sigx + xpysqr
dsigx = (1) * dden  # add gate                                    #(6)
dxpysqr = (1) * dden  # add gate                                  #(6)
# backprop xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# backprop xpy = x + y
dx = (1) * dxpy                                                   #(4)
dy = (1) * dxpy                                                   #(4)
# backprop sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # Notice += > add gradient at branches  #(3)
# backprop num = x + sigy
dx += (1) * dnum                                                  #(2)
dsigy = (1) * dnum                                                #(2)
# backprop sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy                                 #(1)
# done! phew

실제 적용 시 코드 형식

Graph (or Net) object (Rough psuedo code)

class Computaional Gragh(object):
	# ...
    def forward(inputs):
    	# 1. [pass inputs to input gates...]
        # 2. [forward the computational graph:
        for gate in self.graphnodes_topologically_sorted():
        	gate.forward()
    	return loss # the final gate in the graph outputs the loss
 	
    def backward():
    	for gate in reversed(self.graph.nodes_topologically_sorted()):
        	gate.backward() # little piece of backprop (cahin rule applied)
       	return inputs_gradients

multiply gate의 소스코드를 구현해보자.

# x, y, z는 scalars
class MultiplyGate(object):
	def forward(x, y):
    	z = x * y
        self.x = x # must keep thess around(local gradient를 위해)
        self.y = y
        return z
   	def backward(dz): # dz is Global Gradient
    	dx = self.y * dz # [dz/dx * dL/dz]
 		dy = self.x * dz # [dz/dy * dL/dz] 
        retuen [dx, dy]

Vectorized operations

즉, x, y, z가 벡터인 것이다. 그리고 dL/dx, dL/dy, dL/dz 또한 마찬가지다.

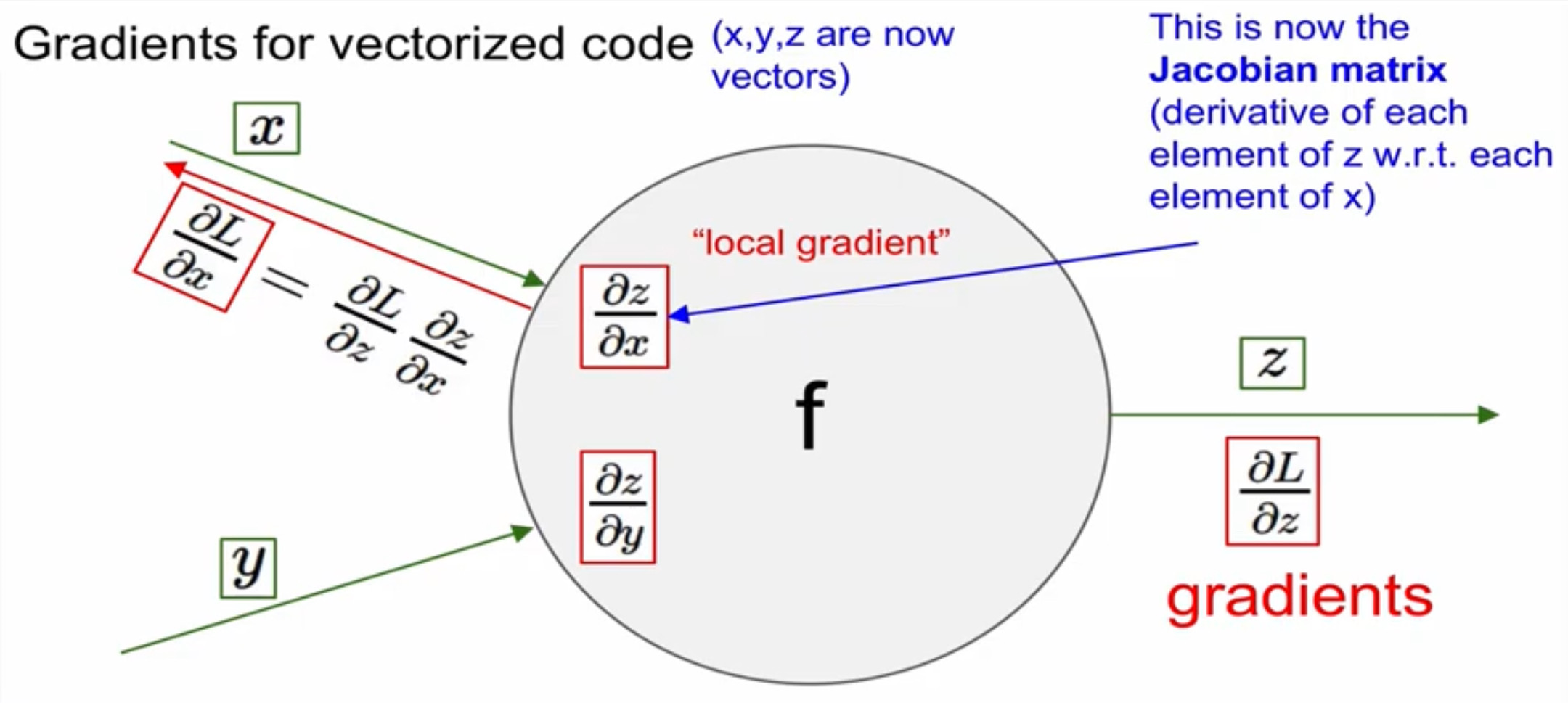
따라서, dz/dx는 matrix가 될 것이다. 이들을 jacobian matrix라고 한다.

• jacobian matirix 하나의 함수가 n개의 변수를 가지고 있을 때, (n차원) 이 함수의 편미분을 모두 구할 수 있는 form의 matrix

즉, 4096-d의 input vector가 들어오면 4096-d의 output vector가 나와야 한다. 이때, jacobian matrix는 [4096, 4096]의 size이다. 형태는 단위행렬의 형태와 비슷하지만, 1뿐이 아닌 0도 혼재되어있을 것이다.

• dL/dx = df/dx * dl/df 에서 df/dx가 jzcobian matrix이다.

실제로는 input vector가 mini batch형태로 전달되므로 (e.g. 100) jacobain matrix는 [409,600, 409600]의 형태를 띨 것이다.

정리

• 인공 신경망은 굉장히 거대하다. gradient, 즉 미분 값들을 하나하나 써내려가는 것은 굉장히 멍청한 방법이다
• 따라서 backpropagation을 사용한다. 이 과정에서 chain rule를 사용해 입력값 및 변수들의 gradient를 계산할 것이다. 이를 위해서 forward, backward pass를 구현한다.
• forward pass는 정방향으로 gate를 거쳐가며 나오는 값을 메모리에 저장한다.(loss & local gradient)
• backward pass는 그 값들을 사용해 역방향으로 chain rule을 활용해 loss function에 대한 input 값들의 gradient를 계산한다. (gradient는 손실함수에 대한 입력 값들의 민감도)