Optimization

• reference : https://cs231n.github.io/optimization-1/ - 2022/11/09

이전 섹션에서 이미지 분류(image classification)을 할 때에 있어 두 가지의 핵심요쇼를 소개했다.

1. 원 이미지의 픽셀들을 넣으면 분류 스코어(class score)를 계산해주는 파라미터화된(parameterized) 스코어함수(score function) (예를 들어, 선형함수).
2. 학습(training) 데이타에 어떤 특정 파라미터(parameter/weight)들을 가지고 스코어함수(score function)를 적용시켰을 때, 실제 class와 얼마나 잘 일치하는지에 따라 그 특정 파라미터(parameter/weight)들의 질을 측정하는 손실함수(loss function). 여러 종류의 손실함수(예를 들어, Softmax/SVM)가 있다.

SVM은 다음과 같은 수식으로 표현할 수 있다.

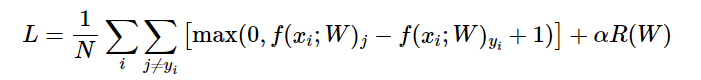
이제 마지막 핵심요소인 최적화(optimization)에 대해 알아보고자 한다. 최적화는 손실함수를 최소화시키는 파라미터(parameter/weight, W)들을 찾는 과정을 뜻한다.

손실함수(loss function)의 시각화

이 강의에서 우리가 다루는 손실함수(loss function)들은 대체로 고차원 공간에서 정의된다. 예를 들어, CIFAR-10의 선형분류기(linear classifier)의 경우 파라미터(parameter/weight) 행렬은 크기가 [10 x 3073]이고 총 30,730개의 파라미터(parameter/weight)가 있다. 따라서, 시각화하기가 어려운 면이 있다. 하지만, 고차원 공간을 1차원 직선이나 2차원 평면으로 잘라서 보면 약간의 직관을 얻을 수 있다.

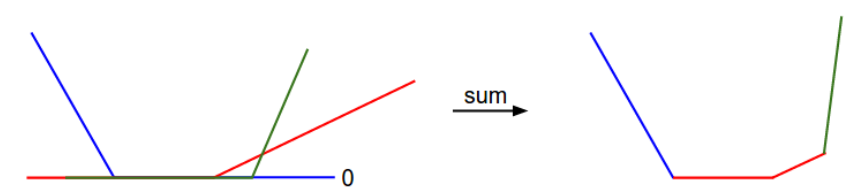
손실(loss)를 1차원으로 표현한 그림. x축은 파라미터(parameter/weight) 하나이고, y축은 손실(loss)이다. 손실(loss)는 여러 항들의 합인데, 그 각각은 특정 파라미터(parameter/weight)값과 무관하거나, 0에 막혀있는 그 파라미터(parameter/weight)의 선형함수이다. 전체 SVM 손실은 이 모양의 30,730차원 버전이다

최적화: Optimization

first method : Random search(무작위 탐색)

단순히 무작위로 파라미터(parameter/weight)를 골라서 넣어보고 넣어 본 값들 중 제일 좋은 값을 기록하는 것이다.

# X_train의 각 열(column)이 예제 하나에 해당하는 행렬이라고 생각하자. (예를 들어, 3073 x 50,000짜리)
# Y_train 은 레이블값이 저장된 어레이(array)이라고 하자. (즉, 길이 50,000짜리 1차원 어레이)
# 그리고 함수 L이 손실함수라고 하자.

bestloss = float("inf") # Python assigns the highest possible float value

for num in range(1000):
  W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
  loss = L(X_train, Y_train, W) # get the loss over the entire training set
  if loss < bestloss: # keep track of the best solution
    bestloss = loss
    bestW = W
  print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)

# prints:
# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# in attempt 3 the loss was 9.278948, best 8.959668
# in attempt 4 the loss was 8.857370, best 8.857370
# in attempt 5 the loss was 8.943151, best 8.857370
# in attempt 6 the loss was 8.605604, best 8.605604
# ... (trunctated: continues for 1000 lines)

CS231n의 강의 안에 따르면, 방법으로 얻은 최선의 W는 정확도 15.5%라고 한다. 무작위 찍기가 단 10%의 정확도인 것이다.

Second method: Random Local Search

처음 떠오르는 전략은, 시작점에서 무작위로 방향을 정해서 발을 살짝 뻗어서 더듬어보고 그게 내리막길길을 때만 한발짝 내딛는 것이다. 구체적으로 말하면, 임의의 W에서 시작하고, 또 다른 임의의 방향 dW으로 살짝 움직여본다. 만약에 움직여간 자리(W + dW)에서의 손실값(loss)이 더 낮으면, 거기로 움직이고 다시 탐색을 시작한다.

W = np.random.randn(10, 3073) * 0.001 # generate random starting W
bestloss = float("inf")
for i in range(1000):
  step_size = 0.0001
  Wtry = W + np.random.randn(10, 3073) * step_size
  loss = L(Xtr_cols, Ytr, Wtry)
  if loss < bestloss:
    W = Wtry
    bestloss = loss
  print 'iter %d loss is %f' % (i, bestloss)

이전과 같은 횟수(즉, 1000번)만큼 손실함수(loss function)을 계산하고도, 이 방법을 테스트 데이터에 적용해보니, 분류정확도가 21.4%로 나왔다. 발전하긴 했지만, 여전히 좀 비효울적인 것 같다

Third method: Following the Gradient

이전까지는 파라미터 공간에서 손실값을 더 낮추는 방향으로 찾는 시도를 할때, 방향을 무작위로 탐색하여 시도했다. 하지만, 수학적으로 손실함수의 gradient를 구해 최선의 방향을 구할 수 있다.

1차원의 함수의 경우, 어떤 점에서 움직일 때 기울기는 함수값의 순간 증가율을 나타낸다. gradient는 기울기라는 것을 변수가 하나가 아니라 여러 개인 경우로 일반화 시킨 것이다. 즉, 그라디언트(gradient)는 입력데이터공간(역자 주: x들의 공간)의 각 차원에 해당하는 기울기(미분이라고 더 많이 불린다)들의 백터이다.

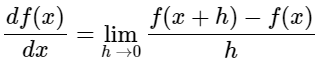
위 그림은 1차원 함수의 미분을 수식으로 쓴 것이다.

numerical gradient

느리고 근사값이지만 쉬운 방법이다.

def eval_numerical_gradient(f, x):

  """
함수 f의 x에서의 그라디언트를 매우 단순하게 구현하기.
- f 는 입력값 1개를 받는 함수여야한다.
 - x는 numpy 어레이(array)로서그라디언트를 계산할 지점 (역자 주: 그라디언트는 당연하게도 어디서 계산하느냐에 따라 달라지므로, 함수 f 뿐 아니라 x도 정해줘야함).
  """

    # evaluate function value at orginal point
    fx = f(x) 
    # Gradient 담을 벡터행렬 초기화 
    grad = np.zeros(x.shape)
    h = 1e-4
    
    # 다차원이기에 for문 대신 iter 사용(x의 모든 index를 다 돌면서 계산)
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite']) 
    while not it.finished:
        
        # 함수 값을 x+h에서 계산하기
        idx = it.multi_index
        temp_val = x[idx]
        x[idx] = temp_val + h

        fxh = f(x) # f(x+h)
        x[idx] = temp_val # 다른 차원에서 편미분하기 위해 원래 값으로 복구 
        # 편미분 계산
        grad[idx] = (fxh - fx) / h
        it.iternext() # 다음 단계로 가서 반복
        
    return grad

이 코드는, 위에 주어진 gradient 식을 이용해서 모든 차원을 하나씩 돌아가면서 그 방향으로 작은 변화 h를 주었을 때, 손실함수의 값이 얼마나 변하는지를 구해서, 그 방향의 편미분 값을 계산한다. 변수 grad에 전체 gradient 값이 최종적으로 저장된다.

위 함수는 아무 함수의 아무 값에서 gradient를 구할 수 있다. 무작위로 뽑은 파라미터 값에서 손실함수(loss function)의 gradient를 구해본다.

# 위의 범용코드를 쓰려면 함수가 입력값 하나(이 경우 파라미터)를 받아야함.
 # 따라서X_train와 Y_train은 입력값으로 안 치고 W 하나만 입력값으로 받도록 함수 다시 정의.

def CIFAR10_loss_fun(W):
  return L(X_train, Y_train, W)

W = np.random.rand(10, 3073) * 0.001 # 랜덤 파라미터 벡터.
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # 그라디언트를 구했다

여기서 손실함수는 SVM 손실함수를 사용했다. 그 코드는 다음과 같다.

def L1(W, X, y):
  
    # compute the loss and the gradient
    num_classes = W.shape[1]
    num_train = X.shape[0]
    loss = 0.0
    
    for i in range(num_train):
        scores = np.dot(X[i], W)
        correct_class_score = scores[y[i]]
        
        for j in range(num_classes):
            if j == y[i]:
                continue
            margin = scores[j] - correct_class_score + 1  # note delta = 1
            if margin > 0:
                loss += margin
    
    # Right now the loss is a sum over all training examples, but we want it
    # to be an average instead so we divide by num_train.
    loss /= num_train
    
    return loss

gradient는 각 차원에서 CIFAR-10의 손실함수의 기울기를 알려주는데, 그걸 이용해서 파라미터를 업데이트한다.

loss_original = CIFAR10_loss_fun(W) # 기존 손실값
print 'original loss: %f' % (loss_original, )

# 스텝크기가 주는 영향에 대해 알아보자.
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
  step_size = 10 ** step_size_log
  W_new = W - step_size * df # 파라미터(parameter/weight) 공간 상의 새 파라미터 값
  loss_new = CIFAR10_loss_fun(W_new)
  print 'for step size %f new loss: %f' % (step_size, loss_new)

# prints:
# original loss: 2.200718
# for step size 1.000000e-10 new loss: 2.200652
# for step size 1.000000e-09 new loss: 2.200057
# for step size 1.000000e-08 new loss: 2.194116
# for step size 1.000000e-07 new loss: 2.135493
# for step size 1.000000e-06 new loss: 1.647802
# for step size 1.000000e-05 new loss: 2.844355
# for step size 1.000000e-04 new loss: 25.558142
# for step size 1.000000e-03 new loss: 254.086573
# for step size 1.000000e-02 new loss: 2539.370888
# for step size 1.000000e-01 new loss: 25392.214036

위 코드에서 W_new로 업데이트할 때, gradient df의 반대방향으로 움직인 것은 손실함수의 증가가 아닌 감소를 원하기 때문이다.

step size는 학습 속도라고도 하는데 얼만큼 변화해야 하는지를 의미하는 하이퍼파라미터이다. 하산 함에 있어서 얼마나 발을 뻗어야할 지와 비견된다. 조금 가는 것은 일관되지만 느리게 최적화를 진행시킨다. 반면에, 그 방향으로 너무 많이 가면, 더 많이 감소시키지만 위험성도 크다. 스텝 크기가 점점 커지면, 결국에는 최소값을 지나쳐서 손실값이 더 커지는 지점까지 가게될 것이다. 스텝 크기(나중에 학습속도라고 부를 것임) 가장 중요한 하이퍼파라미터(hyperparameter)이라서 매우 조심스럽게 결정해야 할 것이다.

numerical gradient는 계산하는데 필요한 자원이 파라미터의 수에 따라 선형적으로 늘어난다. 위 예시에서, 총 30,730의 파라미터가 있으므로 30,731번 손실함수 값을 계산해서 gradient를 구해봐야 딱 한 번 업데이트 할 수 있다. 하지만, 요즘 사용되는 신경망은 수천만개의 파라미터 이상으로 사용한다. 이 때 문제는 심각해진다.

analytic gradient

빠르고 정확하지만 미분이 필요하고 실수하기 쉬운 방법이다.
numerical gradient는 단순하지만, 근사값(그냥 작은 h 값)이라는 점과 계산이 비효율적이라는 것이다. 그저 우리가 원하는 것은 weight가 변할 때, loss가 얼만큼 변하는 건가?이다. 그냥 미분만 알면 되는 것이다.

analytic gradient는 미적분을 이용해서 해석적으로 gradient를 구하는 것인데, 이는 정확한 수식을 이용하기 때문에 계싼이 매우 빠르다. 하지만, 수치적으로 구한 gradient와 다르게, 구현하는데 실수하기 쉽다. 그래서, 해석적으로 구하고 수치적으로 구한 것을 비교하여 틀린 경우 고치는데 이 과정을 gradient check라고 한다.

SVM 손실함수의 예를 들어 설명해보자.

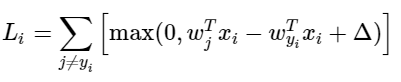
파라미터로 이 함수를 미분하면,

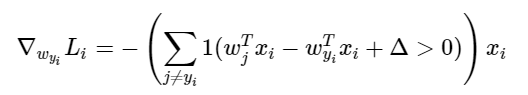
쉽게 말해 괄호 안의 조건이 충족되면 1, 아니면 0인 값을 갖는다. 이렇게 써놓으면 무시무시해보이지만, 실제로 코딩으로 구현할 때는 원하는 차이(마진, margin)을 못 만족시키는, 따라서 손실함수(loss function)의 증가에 일조하는 클래스의 개수를 세고, 이 숫자를 데이터벡터 $x_i$ 에 곱하면 이게 바로 그라디언트(gradient)이다. 단, 이는 참인 클래스에 해당하는 $W$ 의 행으로 미분했을 때의 그라디언트이다. $j \neq y_i$ 인 다른 행에 대한 그라디언트(gradient)는 다음과 같다.

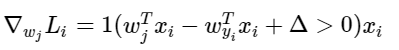
일단 gradient 수식을 구하고 gradient를 업데이트 시키는 것은 간단하다.

Gradient descent

이제 손실 함수의 gradient를 계산할 수 있다. gradient를 반복적으로 평가한 다음 파라미터 업데이트를 수행하는 절차를 기울기 하강법이라고 한다. vanilla 버전은 다음과 같다.

# Vanilla Gradient Descent

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # perform parameter update

이 간단한 loop는 모든 신경망 라이브러리의 핵심이다. 최적화를 수행하는 다른 방법이 있지만, gradient descent는 현재 신경망 loss function을 최적화하는 가장 일반적이로 확립된 방법이다. 수업 내내 이 loop의 세부사항에 대해 몇 가지 변화를 줄 것이지만, gradient descent를 따른다는 핵심 하이디어는 유지될 것이다.

training data는 매우 많을 수 있다. 따라서 단일 파라미터 업데이트를 위해 전체 training set에 대해 전체 손실함수를 계산하는 것은 낭비이다. 이 해결 방법으로 mini batch gradient descent를 사용한다. 예들들어 현재 ConvNets에서는 120만 개의 전체 training set에서 256개의 예시를 포함한 batch를 사용한다. 이 배치를 사용해 파라미터를 업데이트 한다. > SGD 기법 : training set에서 랜덤으로 조금만 가져와서, 그 사진들에 대한 loss를 계산하고, weight를 계산한다.

while True:
  data_batch = sample_training_data(data, 256) # 예제 256개짜리 미니배치(mini-batch)
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # 파라미터 업데이트(parameter update)