Python Numpy를 활용한 Convolution 연산 구현

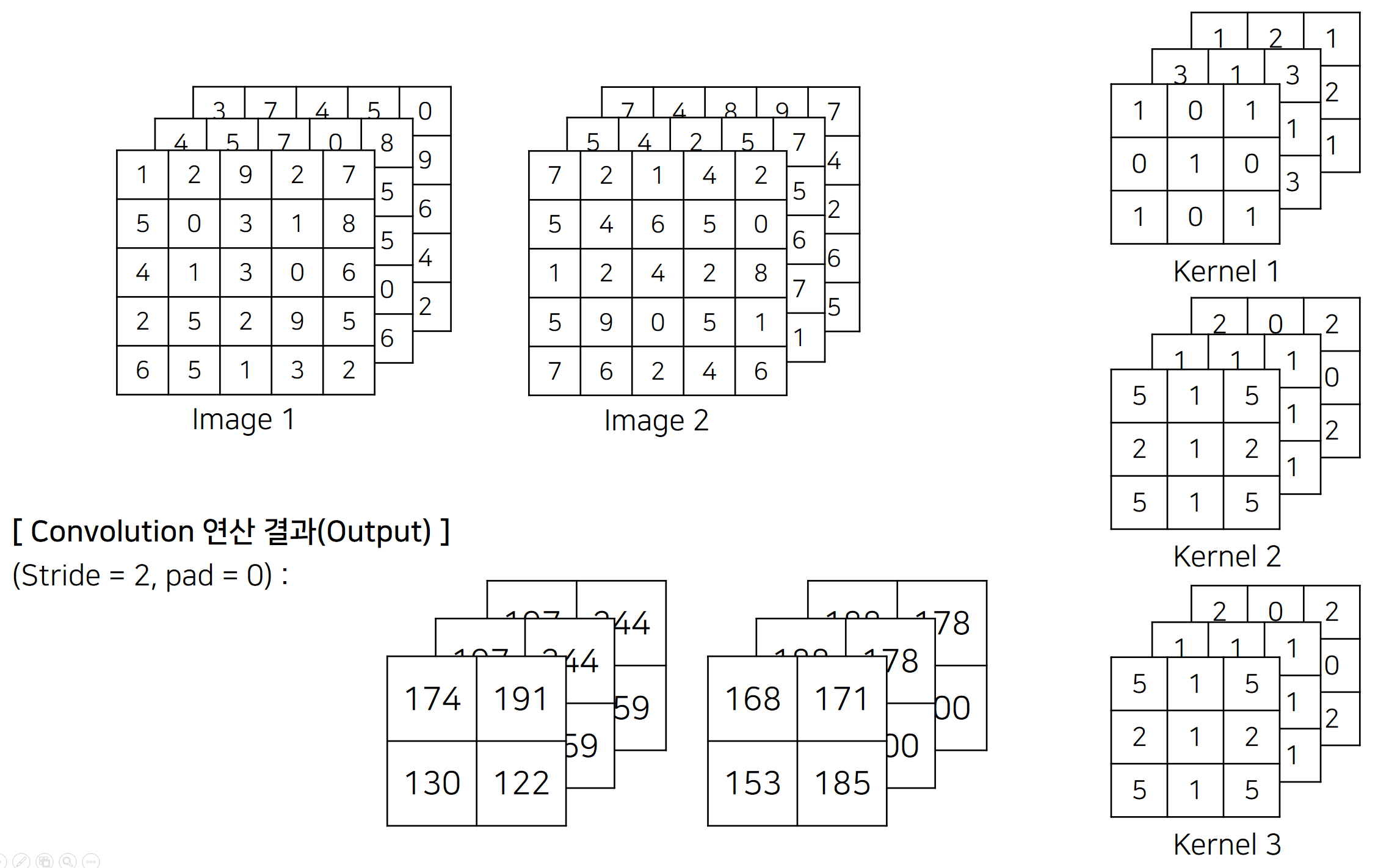
Convolution(합성곱) 연산은 CNN을 포함한 다양한 딥러닝 과정에서 활용되는 연산이다. Pytorch, Keras와 같은 딥러닝 프레임워크에서는 이 Convolution 연산을 기본적으로 제공한다.

*프레임워크(Framework): 응용 프로그램을 개발하기 위한 여러 라이브러리나 묘듈 등을 효율적으로 사용할 수 있도록 하나로 묶어 놓은 일종의 패키지

Convolution 연산에 대한 이해를 높이기 위해 Pythin Numpy를 이용해 Convolution 연산을 구현해보고자 한다.

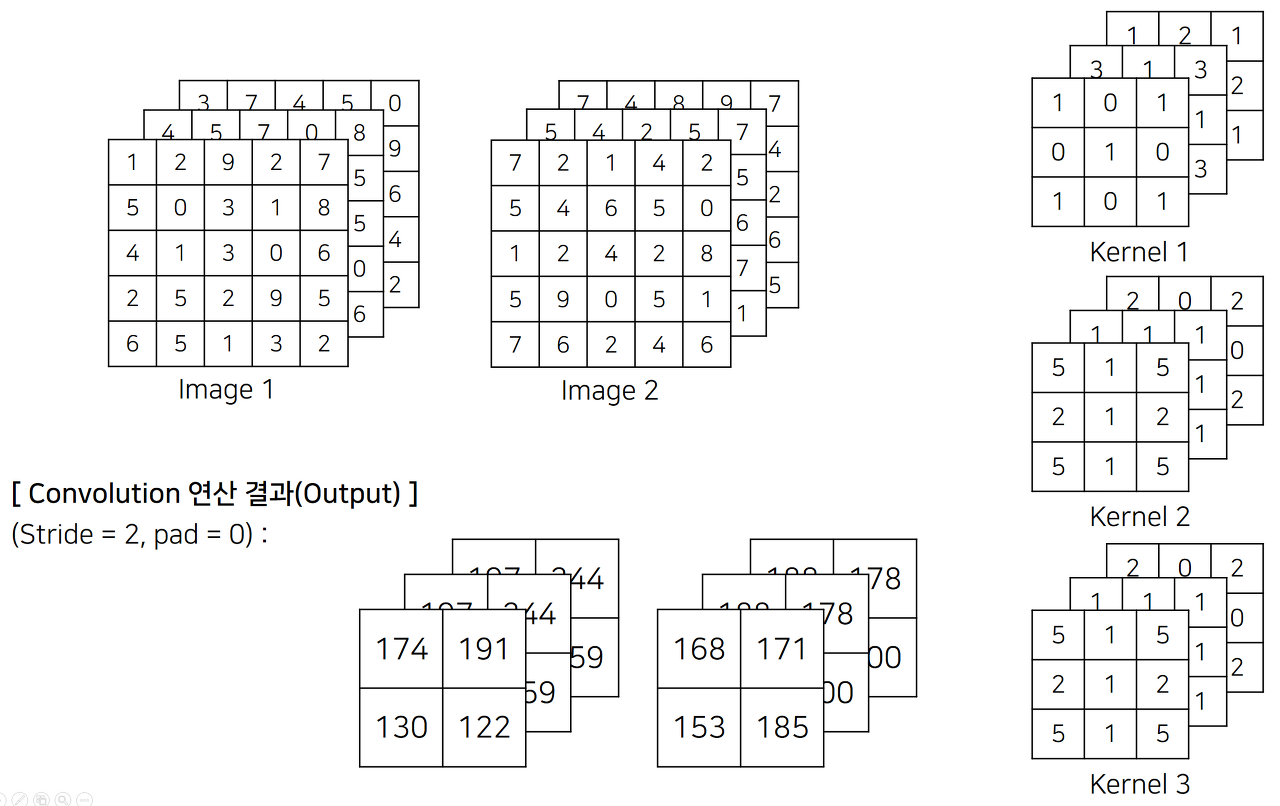
반복문을 이용한 Convolution 연산 구현

Convolution 연산을 구현하는 가장 기본적인 방법은 반복문을 이용하는 것이다.

출력 텐서를 만든 뒤 각각의 원소마다 Convolution 연산을 수행한 결과 값을 채워 넣는 방식으로 Convolution 연산을 구현할 수 있다.

일반적으로 패딩(padding)은 입력 데이터의 높이(height)와 너비(width)에 대해서만 수행한다. Numpy의 경우 패딩을 np.pad() 메서드를 활용해 수행할 수 있다.

또한 Numpu에서 '*'을 활용해 곱셈 연산 수행하면, 원소 단위(element-wise)로 곱셈 연산이 수행된다.

import numpy as np

def conv(input_data, filters, stride=1, pad=0):
    N, C, H, W = input_data.shape
    f_N, f_C, f_H, f_W = filters.shape 
    
    output_H = (H + 2 * pad - f_H) // stride + 1
    output_W=  (W + 2 * pad - f_W) // stride + 1

    # add padding to height and width
    pad_data = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
    
    # make output tensor
    output = np.zeros((N, f_N, output_H, output_W))

    for i in range(N):
        for c in range(f_N):
            for h in range(output_H):
                h_start = h * stride
                h_end = h_start + f_H
                for w in range(output_W):
                    w_start = w * stride
                    w_end = w_start + f_W
                    #element-wise mul
                    output[i, c, h, w] = np.sum(pad_data[i][:, h_start:h_end, w_start:w_end] * filters[c])
    return output

위의 그림을 예제로 결과를 확인해 보자

import numpy as np
from Convolution_by_numpy import conv


X = np.asarray([
# image 1
[
    [[1, 2, 9, 2, 7],
    [5, 0, 3, 1, 8],
    [4, 1, 3, 0, 6],
    [2, 5, 2, 9, 5],
    [6, 5, 1, 3, 2]],

    [[4, 5, 7, 0, 8],
    [5, 8, 5, 3, 5],
    [4, 2, 1, 6, 5],
    [7, 3, 2, 1, 0],
    [6, 1, 2, 2, 6]],

    [[3, 7, 4, 5, 0],
    [5, 4, 6, 8, 9],
    [6, 1, 9, 1, 6],
    [9, 3, 0, 2, 4],
    [1, 2, 5, 5, 2]]
],
# image 2
[
    [[7, 2, 1, 4, 2],
    [5, 4, 6, 5, 0],
    [1, 2, 4, 2, 8],
    [5, 9, 0, 5, 1],
    [7, 6, 2, 4, 6]],

    [[5, 4, 2, 5, 7],
    [6, 1, 4, 0, 5],
    [8, 9, 4, 7, 6],
    [4, 5, 5, 6, 7],
    [1, 2, 7, 4, 1]],

    [[7, 4, 8, 9, 7],
    [5, 5, 8, 1, 4],
    [3, 2, 2, 5, 2],
    [1, 0, 3, 7, 6],
    [4, 5, 4, 5, 5]]
]
])
print('Images:', X.shape)

filters = np.asarray([
# kernel 1
[
    [[1, 0, 1],
    [0, 1, 0],
    [1, 0, 1]],

    [[3, 1, 3],
    [1, 3, 1],
    [3, 1, 3]],

    [[1, 2, 1],
    [2, 2, 2],
    [1, 2, 1]]
],
# kernel 2
[
    [[5, 1, 5],
    [2, 1, 2],
    [5, 1, 5]],

    [[1, 1, 1],
    [1, 1, 1],
    [1, 1, 1]],

    [[2, 0, 2],
    [0, 2, 0],
    [2, 0, 2]],
],
# kernel 3
[
    [[5, 1, 5],
    [2, 1, 2],
    [5, 1, 5]],

    [[1, 1, 1],
    [1, 1, 1],
    [1, 1, 1]],

    [[2, 0, 2],
    [0, 2, 0],
    [2, 0, 2]],
]
])
print('Filters:', filters.shape)

out = conv(X, filters, stride=2, pad=0)
print('Output:', out.shape)
print(out)

실행 결과는 다음과 같고, 결과 값이 같게 나온 것을 알 수 있다.

Images: (2, 3, 5, 5)
Filters: (3, 3, 3, 3)
Output: (2, 3, 2, 2)
[[[[174. 191.]
   [130. 122.]]

  [[197. 244.]
   [165. 159.]]

  [[197. 244.]
   [165. 159.]]]


 [[[168. 171.]
   [153. 185.]]

  [[188. 178.]
   [168. 200.]]

  [[188. 178.]
   [168. 200.]]]]

im2col을 이용한 Convolution 구현

앞서 구현한 반복문의 경우, 행렬 곱을 제대로 활용하지 못한다는 점에서 속도가 느리다. 따라서 메모리를 조금 더 많이 사용하여, 속도를 비약적으로 개선할 수 있는 방법으로 im2col 연산을 활용하는 방법이 있다.

im2col이란 Image to Column의 약자로 다차원의 입력 데이터를 행렬(matrix)로 변환하여 행렬 연산을 하도록 해주는 함수를 말한다.

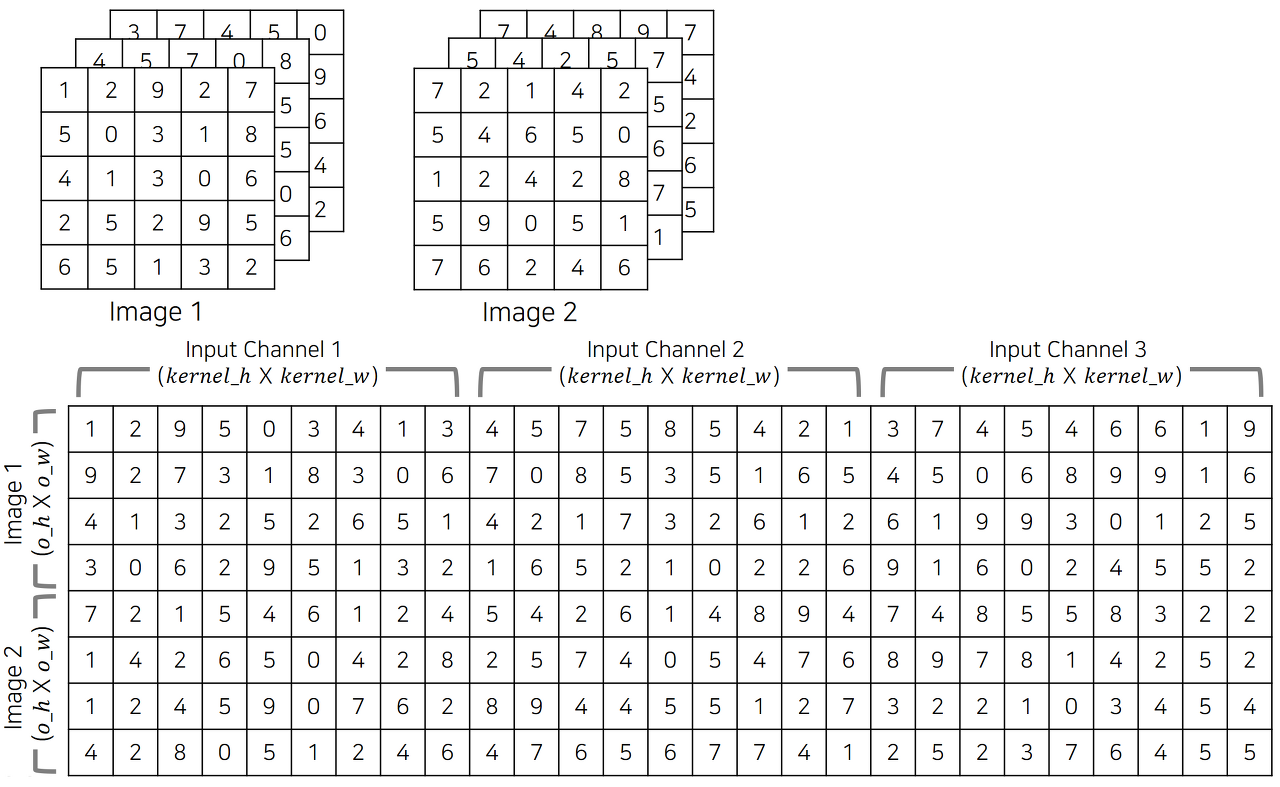
위와 같이 한 배치에 두 장의 이미지가 존재하여 마찬가치로 입력 차원이 (batch size, chnnel size, height, width) = (2, 3, 5, 5)인 예시를 확인 해보연 im2col 연산 후 (8, 27) 차원을 갖는 행렬이 생성되었다. 이는 (이미지 개수 out_h out_w, 입력 채널 개수 kernel_h kernel_w)의 차원을 갖는 행렬이 된다.

https://welcome-to-dewy-world.tistory.com/94

im2col 함수의 코드는 다음과 같이 구현 가능하다.

def im2col(input_data, filters, stride=1, pad=0):
    N, C, H, W = input_data.shape
    f_N, _, f_H, f_W = filters.shape

    output_H = (H + 2 * pad - f_H) // stride + 1
    output_W = (W + 2 * pad - f_W) // stride + 1

    # add padding to height and width
    pad_data = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
    
    # make output tensor
    output = np.zeros((N, C, f_H, f_W, output_H, output_W))

    for y in range(f_H):       
        y_end = y + stride * output_H
        for x in range(f_W):
            x_end = x + stride * output_W
            output[:, : y, x, :, :] = pad_data[:, :, y:y_end:stride, x:x_end:stride]
    
    output = output.transpose(0, 4, 5, 1, 2, 3).reshape(N * output_H * output_W, -1) 

    return output

im2col 함수를 활용한 합성곱 연산의 코드는 다음과 같다.

import numpy as np

def im2col(input_data, filters, stride=1, pad=0):
    N, C, H, W = input_data.shape
    f_N, _, f_H, f_W = filters.shape

    output_H = (H + 2 * pad - f_H) // stride + 1
    output_W = (W + 2 * pad - f_W) // stride + 1

    # add padding to height and width
    pad_data = np.pad(input_data, [(0, 0), (0, 0), (pad, pad), (pad, pad)], 'constant')
    
    # make output tensor
    output = np.zeros((N, C, f_H, f_W, output_H, output_W))

    for h in range(f_H):       
        h_end = h + stride * output_H
        for w in range(f_W):
            w_end = w + stride * output_W
            output[:, :, h, w, :, :] = pad_data[:, :, h:h_end:stride, w:w_end:stride]
    
    output = output.transpose(0, 4, 5, 1, 2, 3).reshape(N * output_H * output_W, -1) 

    return output

X = np.asarray([
# image 1
[
    [[1, 2, 9, 2, 7],
    [5, 0, 3, 1, 8],
    [4, 1, 3, 0, 6],
    [2, 5, 2, 9, 5],
    [6, 5, 1, 3, 2]],

    [[4, 5, 7, 0, 8],
    [5, 8, 5, 3, 5],
    [4, 2, 1, 6, 5],
    [7, 3, 2, 1, 0],
    [6, 1, 2, 2, 6]],

    [[3, 7, 4, 5, 0],
    [5, 4, 6, 8, 9],
    [6, 1, 9, 1, 6],
    [9, 3, 0, 2, 4],
    [1, 2, 5, 5, 2]]
],
# image 2
[
    [[7, 2, 1, 4, 2],
    [5, 4, 6, 5, 0],
    [1, 2, 4, 2, 8],
    [5, 9, 0, 5, 1],
    [7, 6, 2, 4, 6]],

    [[5, 4, 2, 5, 7],
    [6, 1, 4, 0, 5],
    [8, 9, 4, 7, 6],
    [4, 5, 5, 6, 7],
    [1, 2, 7, 4, 1]],

    [[7, 4, 8, 9, 7],
    [5, 5, 8, 1, 4],
    [3, 2, 2, 5, 2],
    [1, 0, 3, 7, 6],
    [4, 5, 4, 5, 5]]
]
])
print('Images:', X.shape)

filters = np.asarray([
# kernel 1
[
    [[1, 0, 1],
    [0, 1, 0],
    [1, 0, 1]],

    [[3, 1, 3],
    [1, 3, 1],
    [3, 1, 3]],

    [[1, 2, 1],
    [2, 2, 2],
    [1, 2, 1]]
],
# kernel 2
[
    [[5, 1, 5],
    [2, 1, 2],
    [5, 1, 5]],

    [[1, 1, 1],
    [1, 1, 1],
    [1, 1, 1]],

    [[2, 0, 2],
    [0, 2, 0],
    [2, 0, 2]],
],
# kernel 3
[
    [[5, 1, 5],
    [2, 1, 2],
    [5, 1, 5]],

    [[1, 1, 1],
    [1, 1, 1],
    [1, 1, 1]],

    [[2, 0, 2],
    [0, 2, 0],
    [2, 0, 2]],
]
])
print('Filters:', filters.shape)

stride = 2
pad = 0
X_col = im2col(X, filters, stride=stride, pad=pad)

N, C, H, W = X.shape
f_N, f_C, f_H, f_W = filters.shape

output_H = (H + 2 * pad - f_H) // stride + 1
output_W = (W + 2 * pad - f_W) // stride + 1

output = np.matmul(X_col, filters.reshape(f_N, -1).T)
output = output.reshape(N, output_H, output_W, f_N)
output = output.transpose(0, 3, 1, 2)

print('Output: ', output.shape)
print(output)