[부스트캠프 AI Tech] U-stage. 5-3

느린 개발자·2021년 2월 25일

부스트캠프 AI Tech

목록 보기

24/35

📌 ML With Graphs

📄 Community

실제 세상에서 우리는 주변에서 여러가지 종류의 군집(Community) 을 볼 수 있다.가령 인간 관계 사이에서, 화학 물질 내부에서 등 어디서나 군집을 발견할 수 있다. 그렇다면 그래프에서 어떻게 군집을 잘 찾고 나눌수 있을까?

일반적으로 각 정점이 한 개의 군집에 속하도록 군집을 나눈다. 이때, 군집을 나누기전에 "어떤것이 군집을 잘 찾고 나눈것일까" 에 대한 정의를 해야한다. 이를 위해 비교 대상이 되는 배치모형 과 유의성을 판단할 기준점 군집성 에 대해 살펴보고 추가적으로 대표적인 군집 탐색 알고리즘에 대해 알아본다.

<참고>
비지도 기계학습 문제인 clustering 과 상당히 유사함을 알 수 있다. 차이점은 clustering은 각 feature vector들을 / community는 각 정점을 그룹으로 만드는데 있다.

✏️ 배치 모형(Configuration Model)

성공적인 군집탐색을 정의하기 앞서 배치모형(Configuration Model) 을 알아야 한다. 배치모형 이란 각 정점의 degree를 보존한 상태에서 링크들을 무작위로 재배치 하여 얻은 그래프를 의미한다.

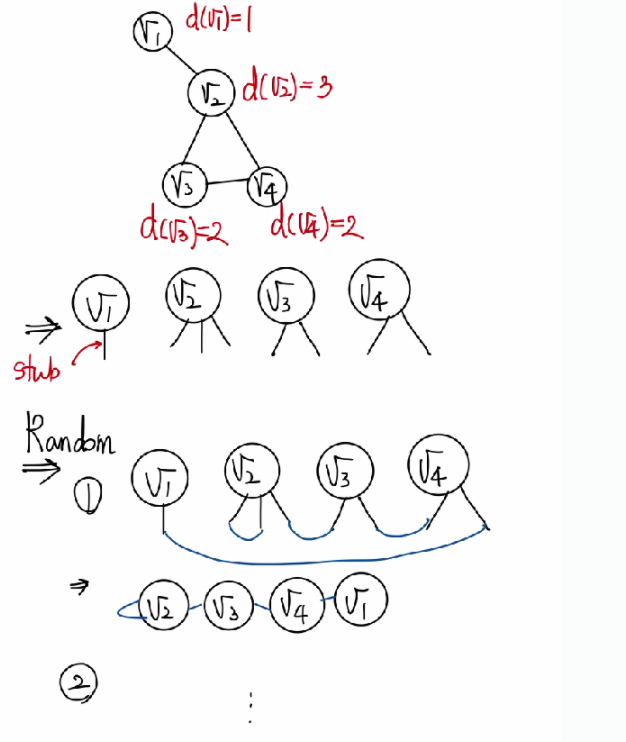
쉽게 설명하면 위의 예시와 같이 각 노드의 degree를 유지한 stub 들을 무작위로 다른 노드의 stub 들과 연결하여 생성된 그래프들 이다. 이때, 배치모형에서 임의의 두 정점 $v_i$ 와 $v_j$ 사이에 간선이 존재할 확률 $p$ 는 두 정점의 degree에 비례하게 된다. 그 이유는 노드 i의 degree 를 $k_i$ 라고 정의했을때, 전체 노드의 degree 의 개수 $\sum_i k_i=2m$ 개로 짝수이다.(각 두개의 노드들이 연결되어야 하기 때문이다.) 그렇다면 $v_i$ 의 하나의 stub 이 $v_j$ 의 stub중 하나와 연결될 확률은 $\frac{k_j}{2m-1}$ 이다. 또한 $v_i$ 의 stub 수(degree)는 $k_i$ 이므로 임의의 노드 $v_i$ 와 $v_j$ 가 연결될 확률은 $\frac{k_i\ast k_j}{2m-1}$ 로 $k_i$ 와 $k_j$ 값에 비례하게 된다.

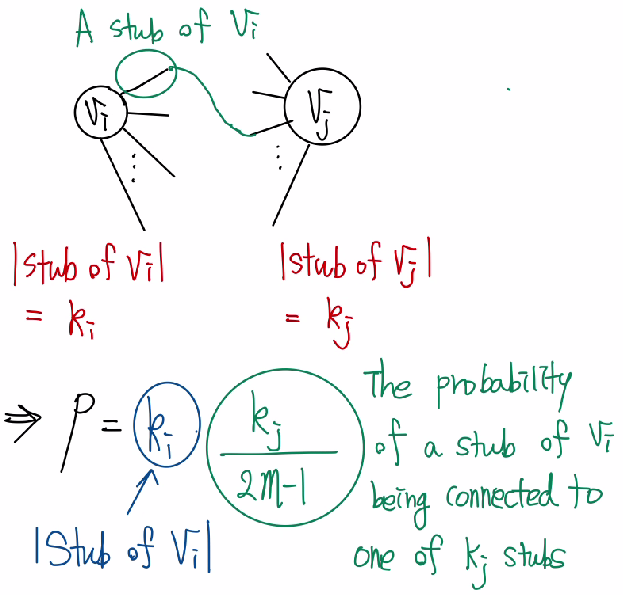
즉, 배치모형이란 n개의 노드와 임의의 두 노드가 연결될 확률 p를 가지는 random graph $G(n,p)$ 를 생성하는 것이다.

✏️ 군집성(Modularity)

성공적인 군집 탐색을 정의하기 위해 필요한 것은 군집성(Modularity) 이다. 어떤 그래프와 군집들의 집합 $S$ 가 주어졌다고 했을때, 각 군집 $s \in S$ 가 군집의 성질을 잘 만족하는지 살펴보기 위해 군집 내부의 간선수를 그래프와 배치모형에서 비교한다. 구체적으로 군집성은 다음 수식으로 계산된다.

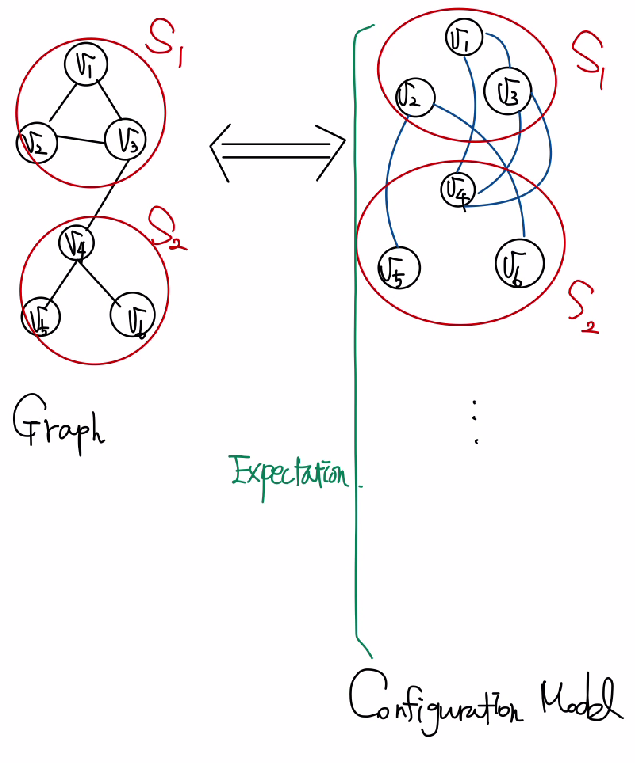
즉, 위 수식의 의미는 현재 그래프에서 군집내의 링크 수가 random graph $G(n,p)$ 로 생성된 그래프들에서 군집내의 링크수보다 클 경우 군집성이 크다는 것이고, 위 값이 충분히 크다는 것은 단순 우연히 찾아낸 군집이 아니라 실질적인 군집일 가능성이 크다는 것이며 통계적으로 유의미 하다는 것이다. 군집성 $M$ 은 항상 $-1\le M\le1$ 의 값을 가지며 ( $\because \sum_id(v_i)=2|E|$ ) 보통 $0.3\le M \le 0.7$ 정도의 값을 가질때 통계적으로 유의미한 군집을 찾아냈다고 할 수 있다.

✏️ 군집 탐색(Community Detection)

✅ Girvan-Newman Algorithm

대표적인 Top-down 군집 탐색 알고리즘 으로 전체 그래프에서 탐색을 시작하여 군집들이 서로 분리되도록 서로 다른 군집을 연결하는 링크(Bridge)를 순차적으로 제거한다. 이때 bridge 를 찾아내기 위해 매개 중심성(Betweennes Centrality)를 이용한다.

매개 중심성 은 다음과 같이 정의 된다.

$\sigma_{i,j}$ :정점 i 에서 정점 j 까지의 최단 경로 수
$\sigma_{i,j}(x,y)$ : 링크 (x,y)를 포함하여 정점 i 에서 정점 j까지의 최단 경로 수 $C_B=\sum_{i<j}\frac{\sigma_{i,j}(x,y)}{\sigma_{i,j}}$

즉, 해당 링크가 정점 간의 최단 경로에 놓이는 횟수가 많을 수록 매개 중심성은 높다. 아래의 예시를 보면 링크 $(v_3,v_4)$ 의 경우 왼쪽에 존재하는 3개의 정점 과 오른쪽에 존재하는 3개의 정점을 연결하기 위해서 반드시 지나야 하는 링크 로 매개 중심성이 가장 높음을 직관적으로 알 수 있다. 반면 $(v_5,v_6)$ 의 경우 낮음을 알 수 있다.

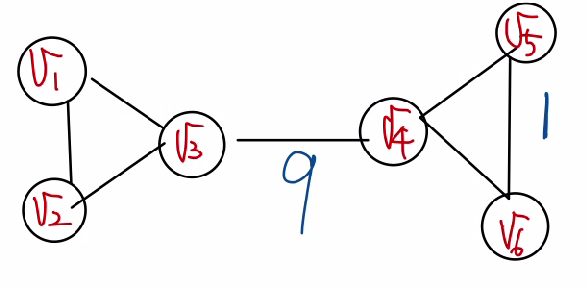
이제 다음의 순차적인 예시를 통해 Girvan-Newman 알고리즘을 살펴보면,

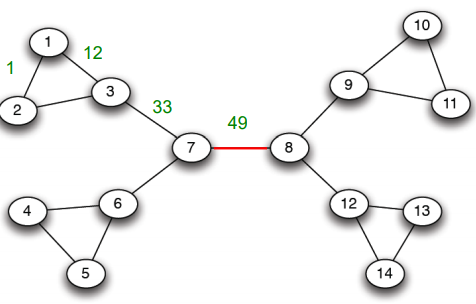
매개 중심성이 가장 높은 링크 $(7,8)$ 를 제거하여 다음 두 군집을 얻는다.

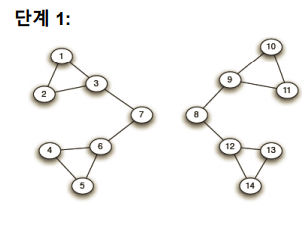
두 군집에서 매개 중심성을 다시 계산하여 매개 중심성이 가장 높은 간선을 제거한다. 이때, 가장 높은 매개 중심성이 여러개라면 모두 제거한다.

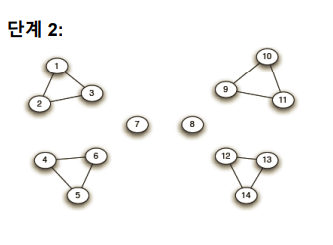
위의 과정을 반복하여 모든 링크가 제거될 때까지 반복한다.

여기서 의문점은 링크의 제거 정도에 따라 다른 입도(Granularity)의 군집구조가 나타나는데 어느정도를 제거하는 것이 좋은것일까?

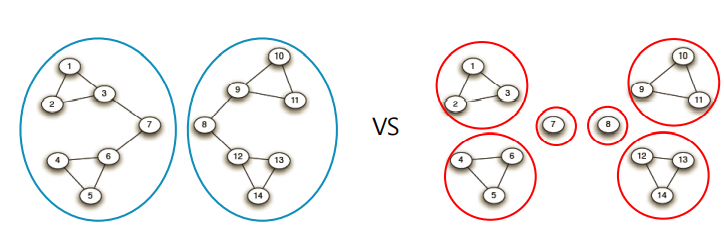
이에 대한 답은 앞서 정의한 군집성 을 기준으로 군집성이 최대가 되는 지점까지 링크를 제거한다. 단, 현재의 연결 요소(Connected Components)들을 군집으로 간주하여 초기 입력 그래프에서의 군집성을 계산한다.

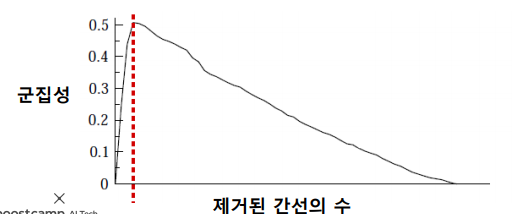
정리하면 Girvan-Newman 알고리즘의 과정은 다음과 같다.

전체 그래프에서 시작한다.
매개 중심성이 높은 순서로 링크를 제거하면서 군집성의 변화를 기록한다.
군집성이 최대화 되는 시점으로 복원한다.
이때의 연결요소를 하나의 군집으로 간주한다.

✅ Louvain Algorithm

대표적인 Bottom-up 군집 탐색 알고리즘으로 개별 노드에서 시작해서 점점 큰 군집을 형성한다. 이때도 역시 군집성을 기준으로 군집성이 최대화 되도록 군집을 형성한다. Louvain 군집 탐색은 크게 두개의 phrase로 구성되는데 구체적인 과정은 다음과 같다.

Phrase1
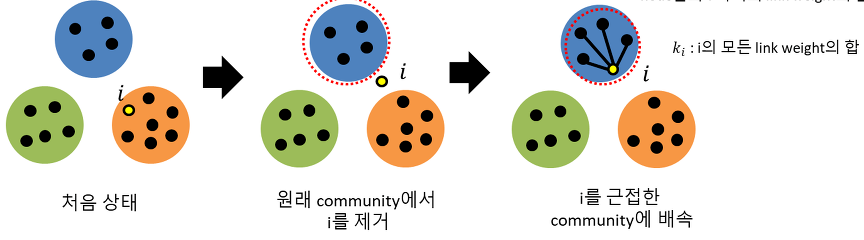
한 노드를 원래의 군집에서 빼내어 인접한 군집에 재배치하였을때의 군집성과 기존의 군집성의 차이를 계산하여 군집성 변화를 측정한다. 측정값을 기준으로 군집성이 가장 큰 폭으로 상승하는 군집에 노드를 재배치 한다. 이 과정을 반복하여 군집성의 변화가 일어나지 않을때까지 수행하며 이를 Modularity Optimization 이라 한다.
Phrase2
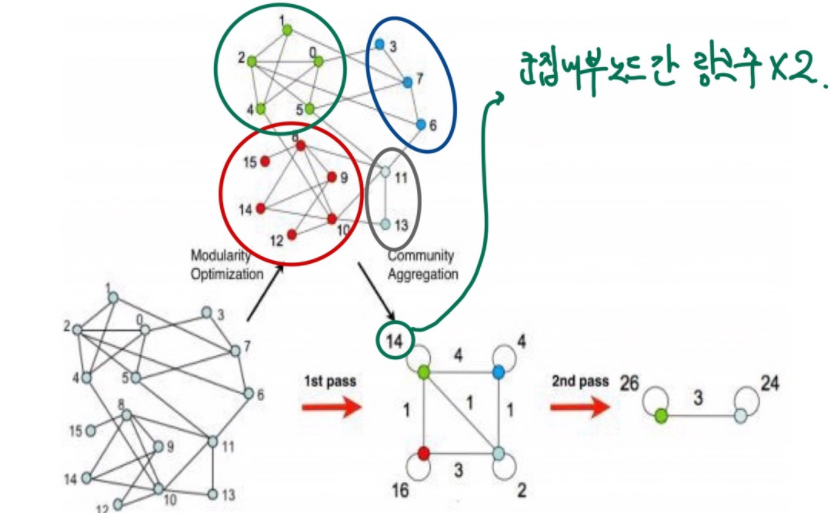
Phrase1 에서 생성된 군집을 바탕으로 군집내부 모든 각 노드간의 link weight(degree)를 합쳐서 self-loop 링크를 가지는 하나의 self-loop 노드로 변환한다. 또 이 과정이 끝나면 다시 phrase 1을 진행하여 phrase 1에서 더이상 변화가 일어나지 않을때 중지한다. 이때, phrase 1 과 pharse 2의 과정을 1 pass 라 한다.

✏️ 중첩 군집 탐색

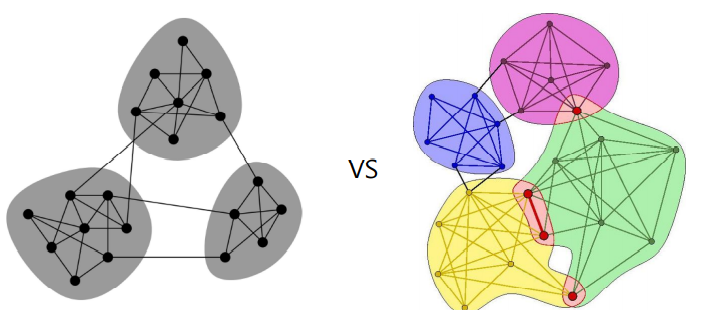
실제 그래프의 군집들은 중첩 되어 있는 경우가 많다. 가령 소셜 네트워크에서의 개인은 여러 사회적 역할을 수행하며 그 결과 여러 군집에 속한다. 하지만 앞서 배운 Girvan-Newman 과 Louvain 알고리즘은 군집간의 중첩이 없다고 가정한다. 그렇다면 중첩이 있는 군집은 어떻게 찾아 낼 수 있을까?

이를 위해 다음과 같은 중첩 군집 모형(Affiliation Graph Model,AGM) 을 가정한다.

각 군집 $i$ 에 대해 같은 군집에 속하는 두 정점은 $p_i$ 의 확률로 링크로 연결된다.
두 정점이 여러 군집에 동시에 속할 경우 링크 연결 확률은 독립적이다.
두 정점 노드 $u$ , $v$ 의 연결 확률은 다음과 같다.
$P(u,v)=1-\prod_{c\in M_u\cap M_v}(1-p_c)$
이때, $M_i$ 는 노드 i가 속해있는 군집 집합이다.
만약 $u$ , $v$ 가 군집을 공유하지 않는다면 $P(u,v)=\epsilon$ 으로 정의한다.

위의 수식 $P(u,v)=1-\prod_{c\in M_u\cap M_v}(1-p_c)$ 을 좀 더 구체적으로 살펴보면, 만약 $u$ , $v$ 가 같은 군집 A 에 포함된다면 $P(u,v)=1-(1-p_A)=p_A$ 이다. 즉 전체확률에서 같은 군집 A의 노드 $u$ , $v$ 가 연결되지 않을 확률을 뺀 것이다. 또한 만약 $u$ , $v$ 가 군집 A,B에 속해 중첩된다면 링크 연결확률이 독립적이라고 가정하였으므로 $P(u,v)=1-(1-p_A)(1-p_B)$ 이다. 즉 전체확률에서 군집 A에서 연결되지 않으면서 군집 B에서 연결되지 않을 확률을 뺀 것이다.

AGM 이 주어지면 주어진 그래프의 확률을 계산할 수 있다.

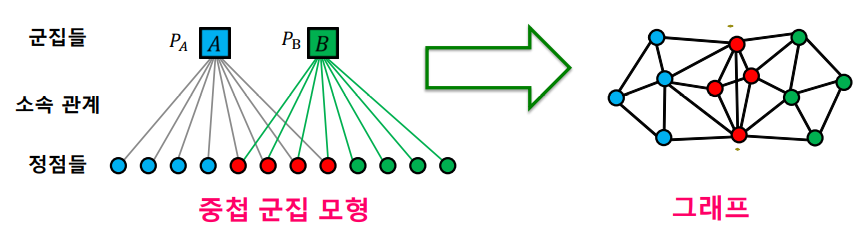
하지만 실제 문제에서는 그래프만 주어지고 AGM이 주어지지 않는 경우가 대다수다. 따라서 그래프를 보고 AGM 을 추정하는것이 목표이다. 이는 주어진 그래프 $G$ 가 나타날 가능성이 가장 높은 AGM $F$ 을 추정하는 문제이며 이것은 MLE(Maximum Likelihood Estimation) 통해 likelihood $P(G|F)$ 를 최대화 하는 $argmax_FP(G|F)$ 인 $F$ 를 찾아 중첩 군집탐색을 진행한다.

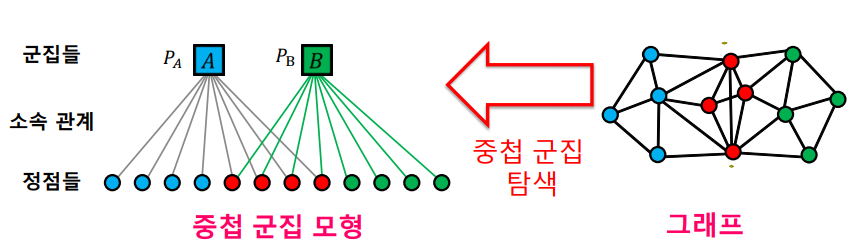
그러나 이 확률분포를 추정하는 것은 매우 어려운 문제다. 그 이유는 각 node가 군집에 속한다 / 속하지 않는다 로 이산적으로 결정되며 discrete optimization은 매우 어려운 문제이기 때문이다. 이러한 문제로 완화된 군집 모형(BigCLAM) 이 제안되는데 이는 각 node가 군집에 속한다 / 속하지 않는다 가 아닌 군집에 속한 정도를 하나의 실수로 표현하는 모형이다. 이 모형이 오히려 현실적일수 있는데 실제로 개인은 조직별로 소속감이 라는 것이 있기 때문이다. 또한 실수라는 연속형 변수로 표현됨으로서 최적화 관점에서 gradient descent도 적용가능하여 확률분포를 추정하기 쉬워진다.

📄 Recommender system

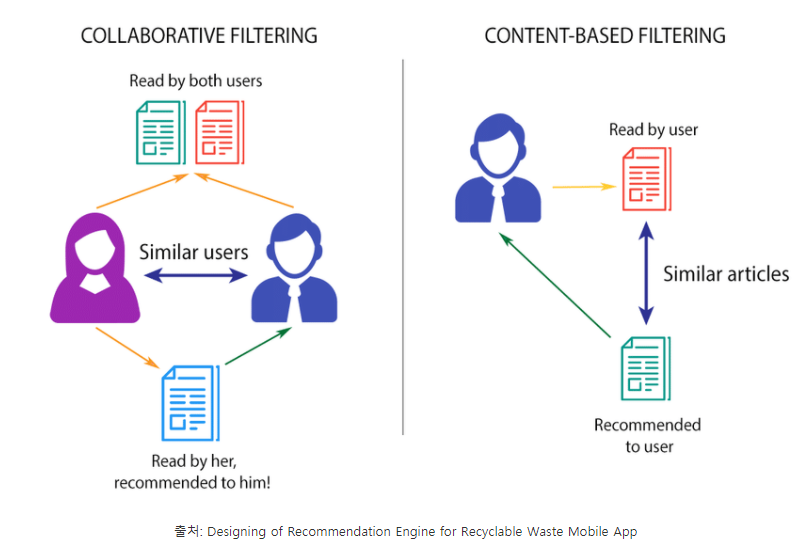
넷플릭스와 유튜브의 컨텐츠 추천, 아마존의 상품 추천 등 우리는 일상생활 속 다양한 곳에서 추천 시스템을 사용하고 있다. 다양한 형태의 추천시스템 중 아이템의 내용을 사용해 추천 해주는 내용 기반 추천(contents based recommendation)과 유저와 아이템간의 유사도를 통해 추천을 해주는 협업 필터링(collaborative filtering)에 대해 살펴보도록 한다.

✏️ Content-based Filtering

내용 기반(Content-based)추천 은 각 사용자가 구매/만족 했던 상품과 유사한것을 추천하는 방법이다. 예를들어,

동일한 장르의 영화를 추천하는것
동일한 감독의 영화 혹은 동일 배우가 출현한 영화를 추천하는것
동일한 카테고리의 상품을 추천하는 것
동갑의 같은 학교를 졸업한 사람을 친구로 추천하는 것
$\dots$

등이 있다. 일반적으로 내용 기반 추천은 다음 네가지 단계로 이루어진다.

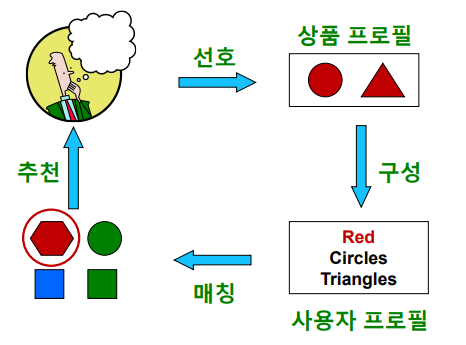
Item profile 을 수집하는 단계
Item profile 이란 해당 상품의 특성을 나열한 벡터이다. 영화추천을 바탕으로 설명하면,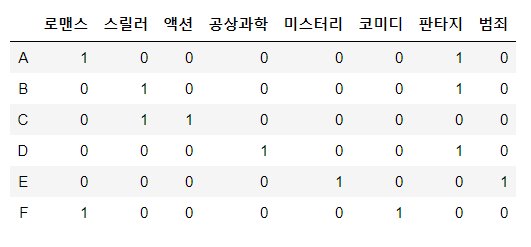

과 같이 one-hot encoding을 통해 item profile을 구성할 수 있다.

User profile 을 구성하는 단계
User profile 은 선호한 상품의 item profile을 implicit data(조회,영상 시청시간,클릭수,구매기록 등) 를 사용하여 가중평균하여 얻은 벡터이다. 이때, implicit data와 TF-IDF matrix(가중평균)의 내적을 통해 user profile을 얻을 수 있다.

User profile 과 다른 item들의 item profile 을 매칭하는 단계
User profile vector $\overrightarrow{u}$ 와 item profile vector $\overrightarrow{v}$ 의 코사인 유사도를 계산한다. 코사인 유사도가 높을수록 해당 사용자가 과거 선호했던 상품들과 해당 상품이 유사함을 의미한다.
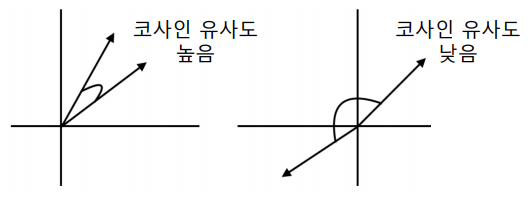
User에게 item을 추천하는 단계
계산한 코사인 유사도를 바탕으로 유사도가 높은 상품들을 사용자에게 추천해준다.

✅ 장점

다른 사용자의 구매기록이 필요하지 않다.
독특한 취향의 사용자에게도 추천이 가능하다.
새 상품에 대해서도 추천이 가능하다.
추천의 이유를 제공할 수 있다.(ex, 로맨스 영화를 선호했기 때문에, 새로운 로맨스 영화를 추천.)

✅ 단점

상품에 대한 부가정보가 없는 경우에는 사용할 수 없다.
구매 기록이 없는 사용자에게는 사용할 수 없다.
지나치게 협소한 추천을 할 위험이 있다.

✏️ TF-IDF(Term Frequency - Inverse Term Frequency)

TF-IDF 는 DTM(Document Term Matrix,다수의 문서에서 등장하는 각 단어들의 빈도를 나타낸 행렬) 내의 각 단어들마다 중요한 정도를 가중치로 주는 방법이다. 주로 문서의 유사도를 구하는 작업, 검색 시스템에서 검색 결과의 중요도를 정하는 작업, 문서 내에서 특정 단어의 중요도를 구하는 작업 등에 쓰일 수 있다.

$tf_{i,j}$ (Term Frequency) : 문서 j 에서 각 단어 i 의 등장 빈도 로 DTM 의 각 단어들이 가지는 값
$df_i$ (Document Frequency) : 특정 단어 i 가 등장한 문서의 수
$N$ : 모든 문서의 수

W_{i,j}=tf_{i,j}\ast log(\frac{N}{1+df_i})

TF-IDF 의 수식을 보면 $df_i$ 의 값이 커질 수록 즉, 특정 단어 i 가 등장한 문서의 수가 많을 수록 가중치는 작아지게 된다. 따라서 해당문서에서는 자주 나타나고( $tf_{i,j}$ ), 다른 문서에서는 많이 안 나오는 단어 ( $log(\frac{N}{1+df_i})$ ) 일수록 중요도가 높다고 판단한다.

✏️ Collaborative Filtering

Collaborative Filtering 은 평점과 같은 명시적(Explicit)인 취향 정보를 바탕으로 추천하는 방법이다. 만약 어떤 특정한 인물 A가 한가지 이슈에 관해서 인물 B와 같은 의견을 갖는다면 다른 이슈에 대해서도 비슷한 의견을 가질 확률이 높을 것이라는 가정에 기반한다. 기본적으로 Collaborative Filtering 에는 Memory-based,Model-based,Hybrid 등이 있지만, 여기선 Memory-based 에 살펴본다.

Memory-based는 유사도를 기반으로 동작하는데, 사용자-사용자 간의 유사도를 기준으로 하는 경우는 User-based / 아이템-아이템 간의 유사도를 기준으로 하는 경우는 Item-based 이다. 구체적으로 User-based에 대해 살펴보면 다음과 같다.

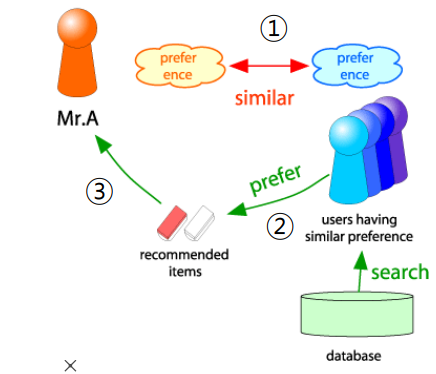
사용자-사용자 간의 유사도를 통해 유사한 취향의 사용자를 찾는 단계
각 사용자가 각 영화에 대해 매긴 평점을 바탕으로 유사도를 평가한다. 이 때 유사도는 코사인 유사도,피어슨 유사도가 사용되는데, 여기선 피어슨 유사도를 바탕으로 설명한다. 이때, 피어슨 유사도는 다음과 같이 정의 된다.

$r_{xs}$ : 사용자 $x$ 가 상품 $s$ 에 대한 평점
$\bar r_{x}$ : 사용자 $x$ 가 매긴 평균 평점
$\bar r_{y}$ : 사용자 $y$ 가 매긴 평균 평점
$S_{xy}$ : 사용자 $x$ 와 $y$ 가 공동 구매한 상품들 $similarity(x,y)=\frac{\sum_{s\in S_{xy}}(r_{xs}-\bar r_{x})(r_{ys}-\bar r_y)}{\sqrt{\sum_{s\in S_{xy}}(r_{xs}-\bar r_x)^2}\sqrt{\sum_{s\in S_{xy}}(r_{ys}-\bar r_y)^2}}$ 피어슨 유사도 는 유저별 평점 기준이 다를수 있으므로 평점 평균을 빼어 정규화후 유사도를 계산하는 것으로 이해할 수 있다. $-1\le similarity(x,y) \le1$ 를 가지며 1에 가까울수록 양의 상관관계, 유사하다 / -1에 가까울 수록 음의 상관관계, 상이하다 라고 판단할 수 있다.구체적으로 다음의 예시를 바탕으로 지수 와 제니 간의 유사도를 구하면 다음과 같다.
$similary(x,y)=\frac{(4-3)(5-3)+(1-3)(1-3)+(5-3)(4-3)}{\sqrt{(4-3)^2+(1-3)^2+(5-3)^2}\sqrt{(5-3)^2+(1-3)^2+(4-3)^2}}\approx0.88$ 즉, 둘의 취향은 양의 상관관계를 가지고 있으며 +1 에 가까우므로 매우 유사함을 판단할 수 있다. 이와 같은 작업을 모든 사용자간의 유사도를 정의하게 되면 사용자 수 x 사용자 수 크기를 가지는 유사도 행렬을 구할 수 있다.

유사한 취향의 사용자들이 선호한 상품을 찾는 단계
사용자가 평가하지 않은 상품의 평점을 추정하기 위해서 위에서 구한 취향의 유사도를 가중치로 사용한 평점의 가중 평균을 통해 평점을 추정한다. 평점을 추정하는 방식에는 크게 상품 $s$ 를 구매한 사용자 중 취향이 가장 유사한 k명의 사용자 $N(x;s)$ 를 뽑아 가중평균하는 방식과 전체를 대상(k=상품 $s$ 를 구매한 전체 사용자의 수)으로 가중평균하는 방식이 있다.전자를 기준으로 살펴보면, 상품 $s$ 에 대한 사용자 $x$ 의 예측 평점 $\hat r_{xs}$ 는 다음과 같이 정의된다.
$\hat r_{xs}=\frac{\sum_{y\in N(x;s)}similarity(x,y)\cdot r_{ys}}{\sum_{y\in N(x;s)}similarity(x,y)}$
구체적으로 유사도 행렬이 계산되었다고 가정했을 때, 제니의 라푼젤 예측평점을 라푼젤을 구매한 사용자(지수,로제)중 가장 유사한 k=2 명의 사용자(음의 상관관계는 제외하여 지수 만 해당한다)를 뽑아 가중평균하여 계산하면 다음과 같다.

- 지수 제니 로제
지수 1 0.88 -0.94
제니 0.88 1 -0.89
로제 -0.94 -0.89 1
$\hat r_{xs}=\frac{0.88*2.0}{0.88}=2.0$
선호한 상품들을 사용자에게 추천하는 단계
예측평점을 바탕으로 평점이 가장 높은 상품들을 추천한다.

-	지수	제니	로제
지수	1	0.88	-0.94
제니	0.88	1	-0.89
로제	-0.94	-0.89	1

✅ 장점

상품에 대한 부가정보가 없는 경우에도 사용할 수 있다.

✅ 단점

충분한 수의 평점데이터가 누적되어야 효과적이다.
새 상품, 새로운 사용자에 대한 추천이 불가능하다.
독특한 취향의 사용자에게 추천이 어렵다.

✏️ Evaluation Metrics

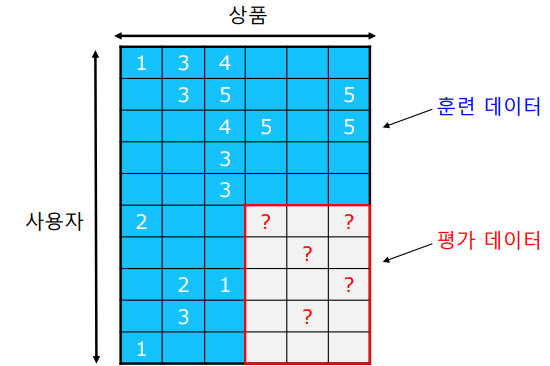
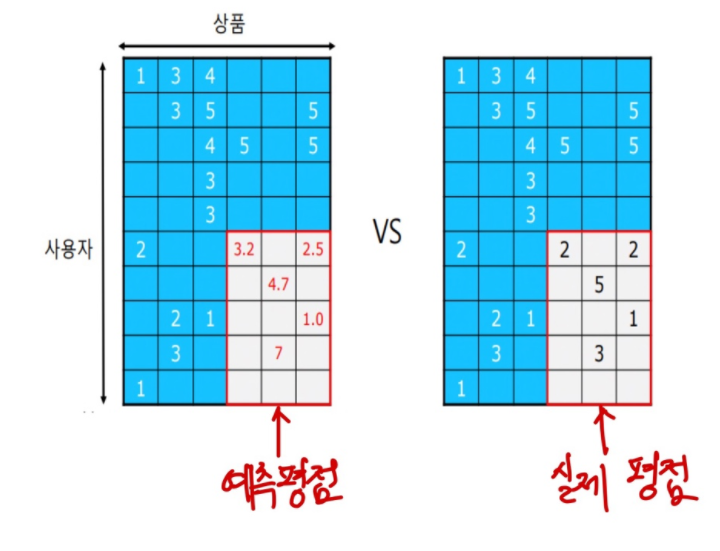
추정한 평점과 실제 평가데이터를 비교하여 오차를 측정한다. 일반적으로 오차를 측정하는 지표로 MSE(Mean Squared Error)가 많이 사용된다. 평가 데이터 내의 평점들의 집합을 $T$ , 사용자 x의 상품 i에 대한 평점 $r_{xi}$ , 예측 평점 $\bar r_{xi}$ 라고 했을때 MSE는 다음과 같이 정의 된다.

MSE=\frac{1}{|T|}\sum_{r_{xi}\in T}(r_{xi}-\bar r_{xi})^2

또한 RMSE(Root Mean Squared Error) 도 많이 사용되는데 다음과 같이 정의 된다.

RMSE=\sqrt{\frac{1}{|T|}\sum_{r_{xi}\in T}(r_{xi}-\bar r_{xi})^2}

주목할 것은 MSE,RMSE 는 예상 평점이 높은 상품과 낮은 상품에 동일한 페널티를 부여한다는 것이다. 하지만 실제로 추천시스템에서는 내가 좋아할 것 같은 상품을 추천해주는것, 즉 예상 평점이 높은 상품을 잘 맞추는것이 중요하다. 이를 고려하여 위의 지표 이외에도 Recall@k,Precision@k,MAP,MRR,NDCG 등의 랭킹 기반 metric을 활용한다.