[부스트캠프 AI Tech] U-stage. 8-1

느린 개발자·2021년 3월 17일

부스트캠프 AI Tech

목록 보기

32/35

📌 Lightweight Modeling

Lightweight modeling techniques 를 이해하기 위한 기초적인 개념 정의와 배경지식을 간단하게 살펴보도록 한다. 그리고 결정 문제 (Decision problem) 와 최적화 문제 (Optimization problem) 의 관계를 이해하여 모델 경량화에서 최적화가 어떤 의미를 지니는지 살펴보도록 한다.

📄 Decision-making

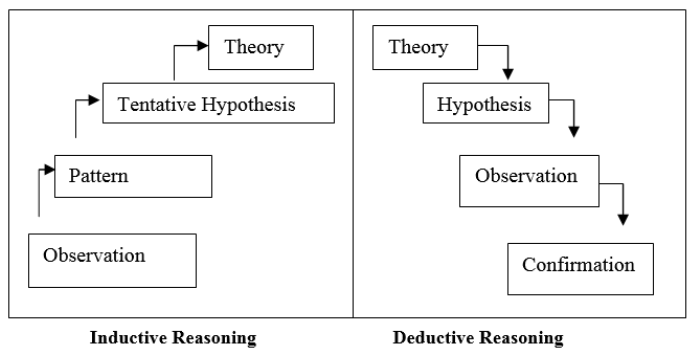
의사결정(Decision-making) 은 여러 대안 중에서 하나의 행동을 고르는 일을 뜻한다. 이것은 다음과 같이 연역적 의사결정(Deductive Decision-making) 과 귀납적 의사결정(Inductive Decision-making) 으로 나뉜다.

✏️ Deductive Decision-making

소크라테스는 인간이다.
모든 인간은 죽는다.
따라서, 소크라테스는 죽는다.

위는 연역법(Deduction) 의 대표적인 예시인 삼단논법으로 연역은 전제와 결론 사이에 필연적인 관계가 있으며 일반적인 원리의 전제로부터 특수 사실을 드러내는 결론을 이끌어 내는것을 말한다.

✏️ Inductive Decision-making

아리스토레텔레스는 그리스 출신이고 똑똑하다.
플라톤은 그리스 출신이고 똑똑하다.
고로 모든 그리스 출신 사람들은 똑똑하다.

귀납법(Induction) 은 전체를 관찰함으로써 일반적인 법칙이나 원칙을 이끌어 내는 것을 말한다. 주목해야할 것은 모델이 데이터를 학습하여 결과를 출력하는 것은 여러 값들 중 하나의 값으로 Inductive Decision-making 하는 과정 이라는 것이다. 즉, 다양한 샘플 데이터를 학습시킴으로써 세상의 다양한 데이터에 대한 일반화를 목적으로 한다. 다시 말하면 샘플데이터로 적절한 가설공간을 추론함으로써 샘플데이터에 맞는 알맞는 가설을 채택하는 과정이다. 하지만 우리는 모든 데이터를 관찰할수 없다는 한계 때문에, 완전환 일반화가 되지 않을수도 있고 오히려 noisy한 데이터라면 엉뚱한 결론을 내릴수도 있다. 또는 샘플데이터 내에서 성립하는 여러 가설들이 다양하게 존재할 수 있다. 이렇게 다양한 가설들이 존재한다면, 귀납적 편향의 문제로 훈련데이터에서는 조건을 만족하였지만 검증데이터에서는 각기 다른 성능을 낼 수 있는 문제가 생긴다. 이와 같이 일반화의 오류, 부당 관찰의 오류, 잘못된 유추의 오류 등 귀납 오류에 의해서 잘못된 일반화를 내릴 수 있으며, 모델을 잘 학습한다는 것은 이러한 오류들을 최대한 제거하여 일반화 성능을 높이는 과정으로 생각해 볼 수 있다.

📄 Edge Computing

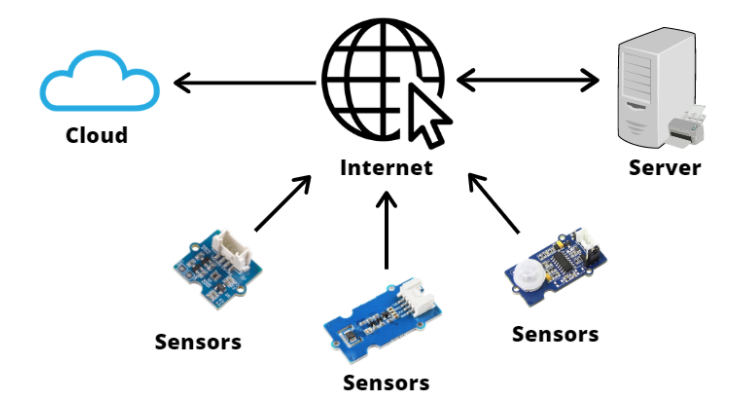
기존의 환경에서는 edge device 가 클라우드 서버에 연결되어 데이터를 전달하고 서버에서 처리된 데이터를 다시 edge device로 넘겨주는 방식이다. 하지만 만약 접속환경이 열악해서 중앙 클라우드에 연결할수 없다면 어떻게 해야할까? 혹여 가능하더라도 발생되는 latency 를 해결할 수 없을까?

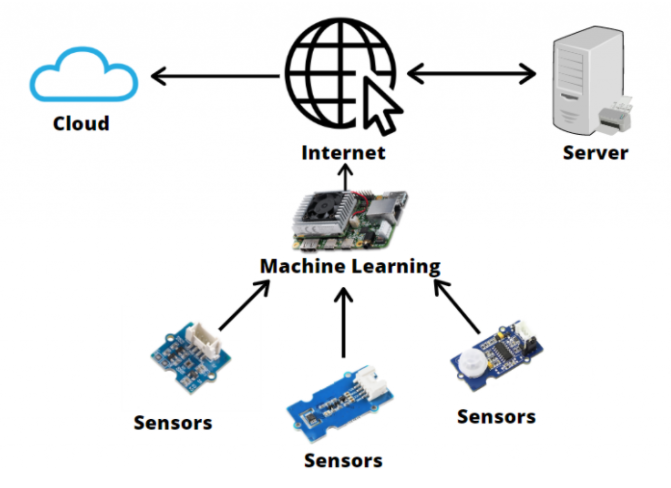
이를 해결하기 위해 Edge Computing 에 주목할 필요가 있다. Edge Computing 을 간단히 설명하면, 클라우드에서 프로세스를 실행하는 대신 컴퓨터, IoT(Internet Of Things), edge device 와 같은 로컬 위치에서 프로세스를 실행하는 것을 말한다. 이것을 AI 모델을 적용하는 것(Edge Intelligence) 으로 생각해보면 edge device에서 데이터를 클라우드에 넘겨서 모델의 inference 결과를 받는 것이 아닌 로컬의 edge device에서 자체적으로 모델의 inference를 진행 하는것으로 생각해볼 수 있다. 그렇다면 Edge Computing이 주는 이점은 무엇일까?

Reduced Costs

클라우드로 보내는 데이터 전송량이 줄어들면서 데이터 통신비와 대역폭 비용이 절감될 수 있다.
Security

보안 카메라, 자율주행차, 드론 등의 경우 AI를 이용할 경우 데이터가 큰 관심사이다. 왜냐하면 많은 데이터들이 개인적인 민감한 정보들을 담고 있기 때문에 클라우드로 보내는 과정에서 개인정보 유출 문제가 발생할 수 있다. 이러한 문제에서 Edge Computing 을 이용하면 로컬에서 데이터를 처리하여 inference를 진행할 수 있으므로 개인정보 유출 문제를 피할 수 있게 된다.

Highly Responsive

중앙 클라우드로 데이터를 보내는 과정이 없기 때문에 latency는 줄어들게 되고 데이터 처리 또는 inferece가 로컬에서 즉시 실행되므로 자율주행차 처럼 빠른 반응이 필요한 어플리케이션에 사용하기에 적합하다.

<참고>

Edge Intelligence (Edge Computing + AI) 패러다임에 대해 더 자세하게 살펴보고 싶다면 여기를 참고하도록 한다.

📄 Lightweight vs Miniaturization

소형화(Miniaturization) 란 단순히 크기를 줄이는 것을 의미하는 반면 경량화(Lightweight) 란 단순히 크기를 줄이는 것이 아닌 필요한 정보는 그대로 가지고 있지만, 불 필요한 정보들을 덜어 내어 크기를 줄여내는 것을 의미한다. 이것이 중요한 이유는 위에서 언급한 Edge Computing 을 위해 구성되는 edge device 들에 모델을 올리기 위해서 inference 성능을 최대한 유지시키면서 크기를 줄이는 것이 목표이기 때문이다. 대표적인 경량화 방법으로는

Pruning
Quantization
Knowledge Distillation
Filter Decomposition
...

등이 있으며, 추후 살펴보도록 한다.

📄 Decision Problem vs Optimization Problem

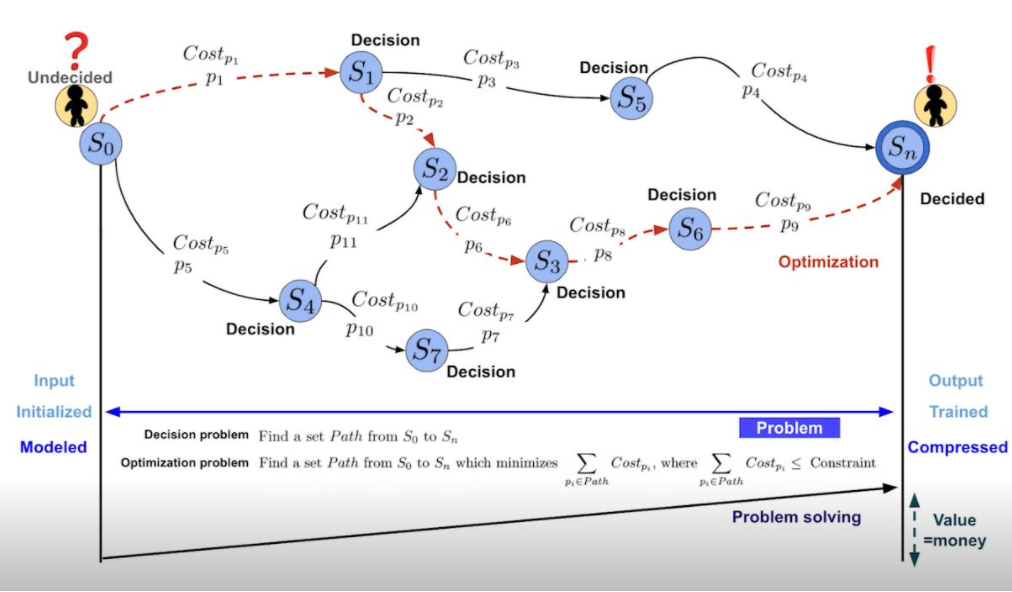
Decision Problem 과 Optimization Problem을 정의하기에 앞서, 기초적인 용어에 대한 정의를 살펴보도록 한다.

✏️ Problem

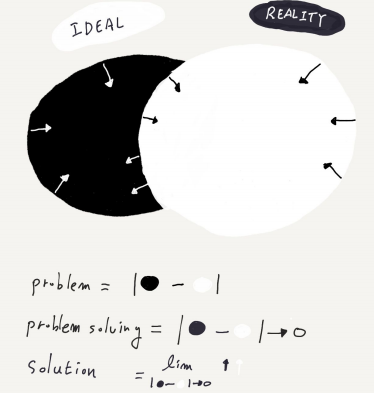
문제(Problem) 란 바라는 것(Terminal State) 과 인식하는 것(Initial State) 의 차이로 정의할 수 있다. 따라서 문제해결(Problem Solving) 은 Initial State 에서 Intermediate States(=decisions) 들을 거쳐서 Terminal State 에 도달하는것으로 생각해 볼 수 있다. 이것을 모델 학습의 관점에서 바라본다면 주어진 데이터셋 (Initial State) 에서 모델 학습(Intermediate State) 을 통해 원하는 결과(Terminal State) 를 얻는것으로 생각해 볼 수 있다.

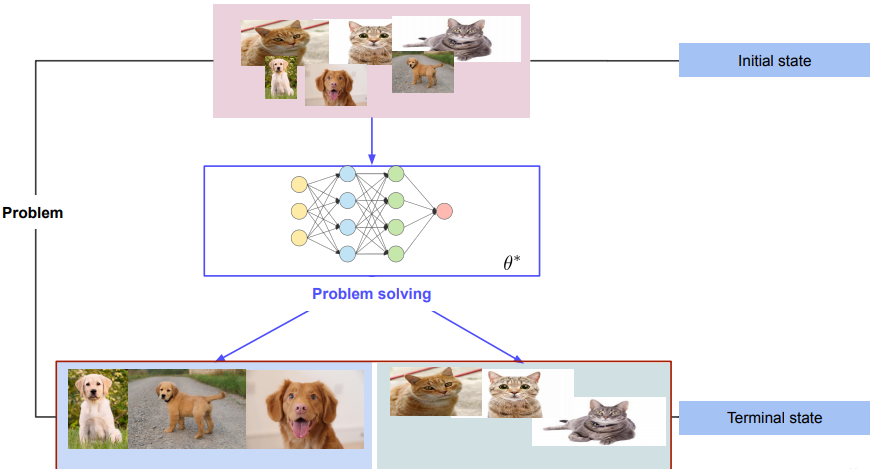
✏️ Computation

Computation 이란 arithmetical / non-arithmetical steps 를 모두 포함한 계산이며 이를 통해 well-defined model(e.g. algorithm)을 생성하는 것을 말한다. 즉, 주어진 입력으로부터 문제의 해법을 찾는 것으로 정의될 수 있다. 그렇다면 well-defined 란 무엇을 의미할까?

어떤 표현을 정의했을 때 명확한 한 가지 의미로 해석 가능할 경우, 즉 주어진 대상이 유일하게 존재할 경우 well-defined 라고 정의한다. 가령, $A=A_0\cup A_1$ 인 집합에 대해 함수 $f: A \rightarrow \{0,1\}$ 가 다음과 같이 정의 된다고 가정한다면,

f:\begin{Bmatrix} f(a)=0, \ if\ a\in A_0\\ f(a)=1, \ if\ a\in A_1 \end{Bmatrix}

만약 $A_0\cap A_1=\phi$ 라면, $f$ 는 well-defined 이다. 하지만 만약 $A_0\cap A_1\not=\phi$ 이라면 $f$ 는 well-defined 이지 않다. 예를들어, $A_0=\{2\},A_1=\{2\}$ 라면 $a\in A_0\cap A_1$ 에 대해 가질수 있는 값은 $(a,0)\in f$ , $(a,1)\in f$ 로 유일하지 않기 때문이다.

✏️ Decision Problem

결정 문제(Decision Problem)는 어떤 형식 체계에서 예/아니오 답이 있는 질문을 말한다. 가령, 모델 학습 관점에서 생각해본다면 "validation loss 가 k 이하인 모델을 찾을 수 있니?" 라는 질문으로 생각해 볼 수 있다.

✏️ Optimization Problem

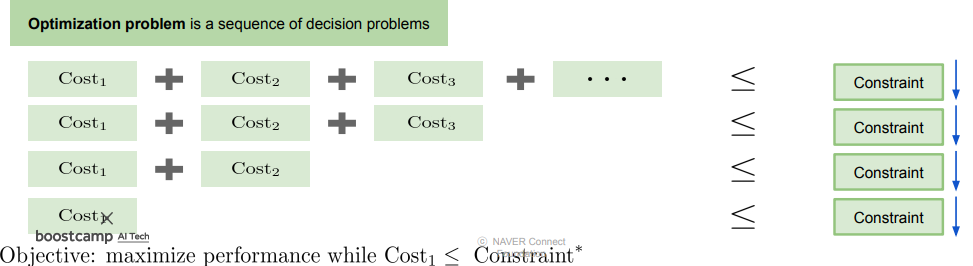
최적화 문제(Optimization Problem) 는 제약조건(Constraints) 하에 비용을 최소화하면서 목적을 달성하는 문제를 말한다. 만약 제약조건이 inference time 이라면 inference time 을 최소화 하면서 inference performance를 높이는 것으로 생각해 볼 수 있다. 따라서 최적화 문제 는 여러 단계의 Decision Problem으로 이루어져 cost를 최소화 할때까지 찾아가는 과정으로 생각해 볼 수 있다. 또한 Model compression 입장에서 생각해본다면 edge device 에 모델을 탑재하기 위해 기존의 모델을 제약조건(inference time, model size, $\dots$ ) 하에 inference performance 를 높이는 것으로 생각해 볼 수 있다.