[부스트캠프 AI Tech] U-stage. 8-2

느린 개발자·2021년 3월 17일
부스트캠프
1

부스트캠프 AI Tech

목록 보기
33/35

📌 Lightweight Modeling

경량화의 목적 중 하나인 모델의 시간복잡도를 줄이는 방법과 압축(Compression) 에 대해 살펴보도록 한다. 또한 정보이론의 entropy 를 이해하여 딥러닝에서 널리 활용되고 있는 cross-entropy 의 개념을 파악하도록 한다.

📄 Algorithm

✏️ Big-O Notation

✏️ Time Complexity vs Space Complexity

✏️ P = NP ?

✏️ Reduction

✏️ NP Complete

✏️ Approximation Algorithm

📄 Information Theory

딥러닝에서 빈번하게 등장하는 정보 이론(Information Theory) 의 기본적인 개념들을 살펴 보도록 한다.

✏️ Information Content

질량, 높이, 속도 와 같은 것들을 단위량을 가지고 측정하고 비교하듯, 우리가 삶 속에서 매일 교환하는 "정보" 에 대한 단위량 을 정의하고 싶었다. 이에 Claud Shannon 은 정보량(Information Content) 을 "어떤 내용을 알기 위해 물어봐야 하는 최소한의 질문 개수" 라고 정의하였다. 가령, 동전을 던져 나온 결과가 앞면 / 뒷면 인지를 알기 위해서는 1번의 질문 만 있으면 된다. 즉, "앞면이니?" 이라고 질문을 했을 때 "아니오" 라는 답변이 나왔다면, 뒷면 / "예" 라는 답변이 나왔다면 앞면 임을 알 수 있다. 따라서 앞 뒤가 나올 확률이 똑같은 동전 의 결과를 표현하기 위해서는 1번의 질문 만 있으면 표현할 수 있고, 다르게 말하면 1 bit 만 있다면 동전의 결과를 표현할 수 있다. 이를 수식으로 표현하면 다음과 같이 표현할 수 있다.

2질문개수=나올 수 있는 결과의 수2^{질문개수}=나올\ 수\ 있는\ 결과의\ 수 \\
⇒21=2⇒log⁡2(2)=1 bit\begin{aligned} &\Rightarrow2^1=2 \\ &\Rightarrow \log_2(2)=1\ bit \end{aligned}

또 다른 예시로 정육면체의 주사위를 던진다고 가정했을 때, 필요한 질문개수는 다음과 같이 표현할 수 있을 것이다.

2질문개수=6⇒log⁡2(6)≈2.58 bits\begin{aligned} 2^{질문개수}&=6 \\ \Rightarrow \log_2(6)&\approx2.58\ bits \end{aligned}

위의 예시에서 주목해야 할것은 두 가지인데,

  1. 주사위 예시가 정보량이 더 많고, 이것은 상대적으로 어떤 값일지 모르는 불확실성(uncertainty)이 높다는 것을 의미한다.

  2. 주사위 예시를 기준으로 확률의 관점에서 정보량을 표현한다면, 다음과 같다.

    log⁡2(6)=−log⁡2(16)≈2.58 bits\log_2(6)=-\log_2(\frac{1}{6})\approx2.58\ bits

    즉, 정보량 은 다음과 같이 표현할 수 있다.

    I(x)=−log⁡2(p(x))I(x)=-\log_2(p(x))

    이것은 어떤 사건이 일어날 확률이 작을수록(빈번하게 일어나지 않는 사건일수록) 새롭게 얻을 정보가 많다는 것 이며 불확실성이 커지는 것을 의미한다.

✏️ Entropy

Entropy=H(x)=Ex∼p[I(x)]=−∑xp(x)log⁡2(p(x))Entropy=H(x)=E_{x\sim p}\begin{bmatrix} I(x) \end{bmatrix}=-\sum_x p(x)\log_2(p(x))

Entropy 는 정보량(Information Content)의 기대값 으로 불확실성(Uncertainty) 를 나타내는 척도 이다. 동전 던지기 예시를 다시 한번 생각해보면, random variable xx 는 2개의 값(앞면=1,뒷면=0)을 가진다. 이때 Entropy 는

Entropy=−∑x12log2(12)=−2∗12log2(12)=1 bitEntropy=-\sum_x\frac{1}{2}log_2(\frac{1}{2})=-2\ast\frac{1}{2}log_2(\frac{1}{2})=1\ bit

로 1 bit 의 평균 정보량을 가지는 것으로 확인할 수 있다. 즉 임의의 데이터 한개를 전송하기 위한 평균 bit 는 1 임을 의미한다. 그렇다면 만약 찌그러진 동전이 있어서 앞면 / 뒷면 나올 확률이 (앞면,뒷면)=(23,13)(\frac{2}{3},\frac{1}{3}) 이라면 어떤 결과가 나올까?

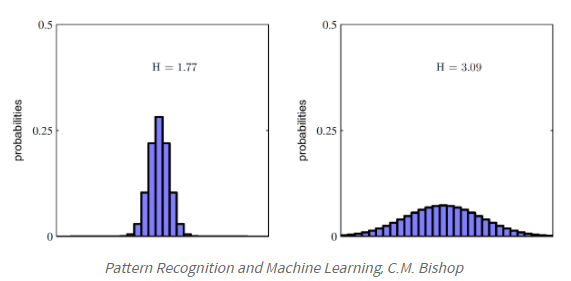
Entropy=−∑xp(x)log⁡2(p(x))=−{p(x=1)log⁡2(p(x=1))+p(x=0)log⁡2(p(x=0))}=−{23log⁡2(23)+13log⁡2(13)}≈0.918 bit\begin{aligned} Entropy&=-\sum_xp(x)\log_2(p(x))\\ &=-\begin{Bmatrix} p(x=1)\log_2(p(x=1))+p(x=0)\log_2(p(x=0)) \end{Bmatrix}\\ &=-\begin{Bmatrix} \frac{2}{3}\log_2(\frac{2}{3})+\frac{1}{3}\log_2(\frac{1}{3}) \end{Bmatrix}\\ &\approx0.918\ bit \end{aligned}

위의 두 예시에서 주목해야할 것은 찌그러진 동전 던지기(Non-uniform distribution) 가 동일한 확률을 가지는 동전던지기(Uniform distribution) 보다 엔트로피가 낮다 는 것이다. 즉, 찌그러진 동전던지기 가 더 정보량이 적고 , 그만큼 불확실성이 낮다 는 것을 의미한다. 아래의 그림을 보면 대체적으로 균등한 pp의 distribution 보다 한쪽으로 치우쳐진(deterministic) pp의 distribution 의 엔트로피가 더 낮음을 확인할 수 있다.

✏️ Cross-entropy

H(P,Q)=−∑xp(x)log⁡(q(x))H(P,Q)=-\sum_xp(x)\log(q(x))

Cross-entropy는 Estimated Probability Distribution QQ 와 True Probability Distribution PP가 얼마나 근사하지를 살펴보는 것을 의미한다. 그렇다면 이것이 딥러닝의 cost function 으로 가지는 의미는 무엇일까?

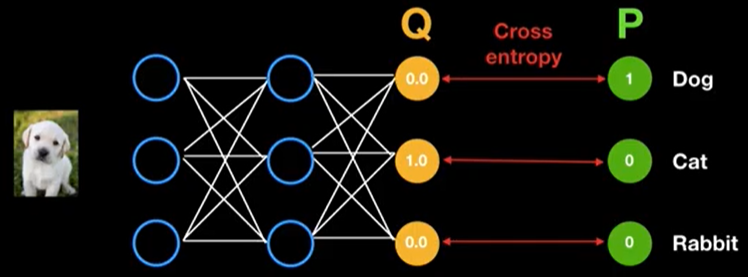
우선 초기 학습 단계에서는 위와 같이 모델을 통한 예측 분포 QQ 는 실제 분포 PP 와 근사하지 않을 것이다.

H(P,Q)=−(1∗log⁡2(0.0)+0∗log⁡2(1.0)+0∗log⁡2(0.0))=∞H(P,Q)=-(\textcolor{green}{1}\ast\log_2(\textcolor{orange}{0.0})+\textcolor{green}{0}\ast\log_2(\textcolor{orange}{1.0})+\textcolor{green}{0}\ast\log_2(\textcolor{orange}{0.0}))=\infin

즉, Entropy 가 아주 크고 이것은 불확실성이 아주 큰 것을 의미함과 동시에 새롭게 얻을 정보(새롭게 학습할 정보)가 많다는 것을 의미한다. 따라서 모델은 불확실성을 줄이는 방향으로 학습해 나갈 것이다.

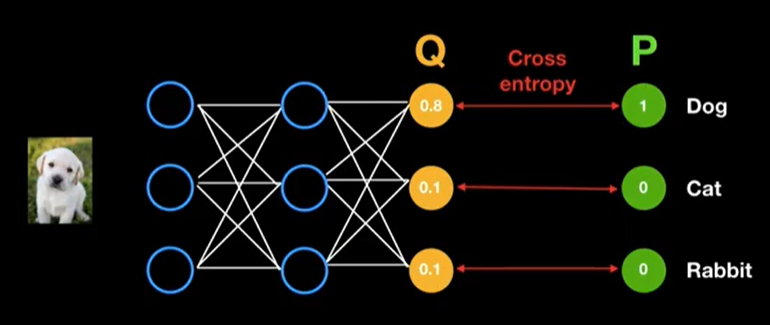
학습이 어느정도 진행된 후에는 예측 분포 QQ 는 실제 분포 PP 와 근사해졌을 것이다.

H(P,Q)=−(1∗log⁡2(0.8)+0∗log⁡2(0.1)+0∗log⁡2(0.1))≈0.32H(P,Q)=-(\textcolor{green}{1}\ast\log_2(\textcolor{orange}{0.8})+\textcolor{green}{0}\ast\log_2(\textcolor{orange}{0.1})+\textcolor{green}{0}\ast\log_2(\textcolor{orange}{0.1}))\approx0.32

즉, 원하는 방향으로 학습이 된다는 것은 새로운 얻은 정보들을 학습하여 Entropy가 작아지도록 / 불확실성이 작아지도록 하는것을 의미한다.

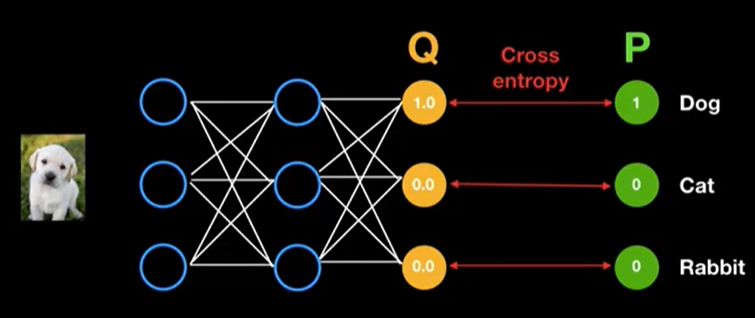
최종적으로 아주 이상적인 방향으로 학습이 되었다고 가정하면, 위와 같은 결과를 얻을 수 있을 것이다.

H(P,Q)=−(1∗log⁡2(1.0)+0∗log⁡2(0.0)+0∗log⁡2(0.0))=0H(P,Q)=-(\textcolor{green}{1}\ast\log_2(\textcolor{orange}{1.0})+\textcolor{green}{0}\ast\log_2(\textcolor{orange}{0.0})+\textcolor{green}{0}\ast\log_2(\textcolor{orange}{0.0}))=0

즉, Entropy가 0 이 되어 불확실성이 완전히 제거된 상태이며 더이상 학습할 새로운 정보가 없음을 의미한다.

✏️ KLD(Kullback–Leibler Divergence)

DKL(P∥Q)=∑xp(x)log⁡(p(x)q(x))=−∑xp(x)log⁡(q(x))+∑xp(x)log⁡(p(x))=H(P,Q)−H(P)\begin{aligned} D_{KL}(P\|Q)&=\sum_xp(x)\log(\frac{p(x)}{q(x)})\\ &=-\sum_xp(x)\log(q(x))+\sum_xp(x)\log(p(x))\\ &=H(P,Q)-H(P) \end{aligned}

KLD 는 두 확률 분포 PP,QQ 의 다름의 정도 를 수치화하여 기본적으로 두 확률 분포를 비교하기 위해 사용된다.(상대 엔트로피(Relative Entropy) 라고도 불린다.) 이를 이해하기 위해서는 Likelihood Ratio(LR) 에 대해 알아야 할 필요가 있다.

LR 이란

Bayesian 관점에서 보면 KLD 는 prior distribution QQ 에서 posterior distribution PP 로 이동할 때 얻어지는 정보의 양 을 의미한다.

  1. 항상 0 이상의 값을 갖는다.

  2. 비대칭적(Asymmetric)이다.

  3. 두 확률 분포가 동일 할 때 KLD 는 0 이 된다.

📄 Model Search

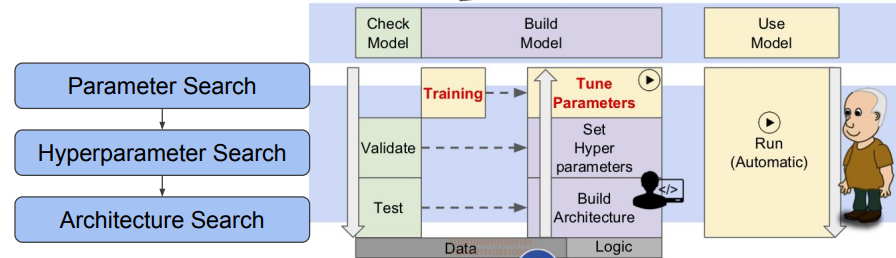
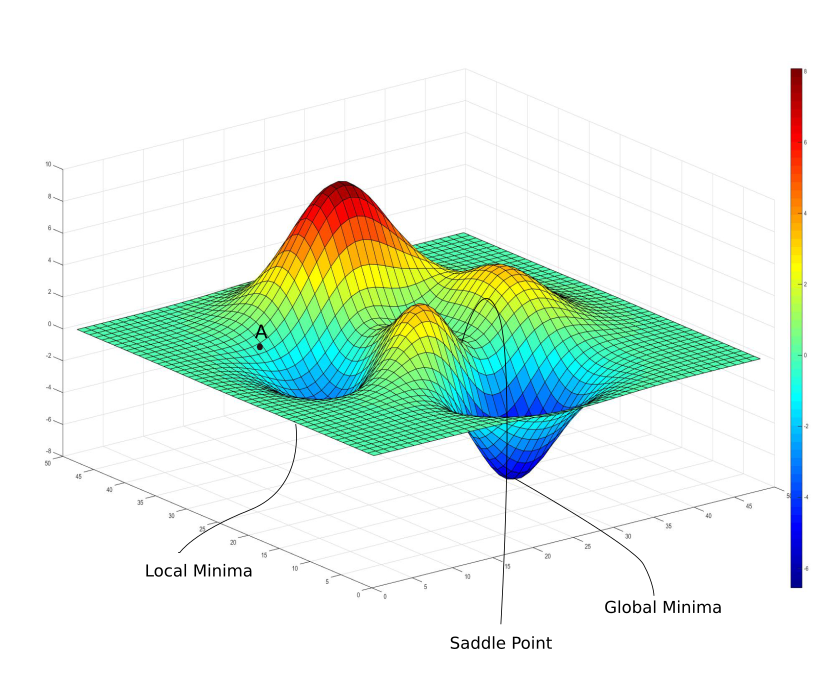
Parameter Search 는 잘 알고 있듯이 모델을 학습하여 최적의 weight를 찾는 탐색 과정을 뜻한다. 하지만 전체 search space(해가 될 수 있는 가능성이 있는 집합) 를 살펴볼 수 없기 때문에 global minima / local minima 인지를 파악하기 어렵다. 또한 plateau 에 빠지게 되면 학습이 더디게 되거나 더이상 학습이 진행되지 않을 수도 있다. 그래서 Adam,SGD, …\dots 와 같은 optimizer를 통해 최적의 weight를 가지는 global minima를 찾는다.

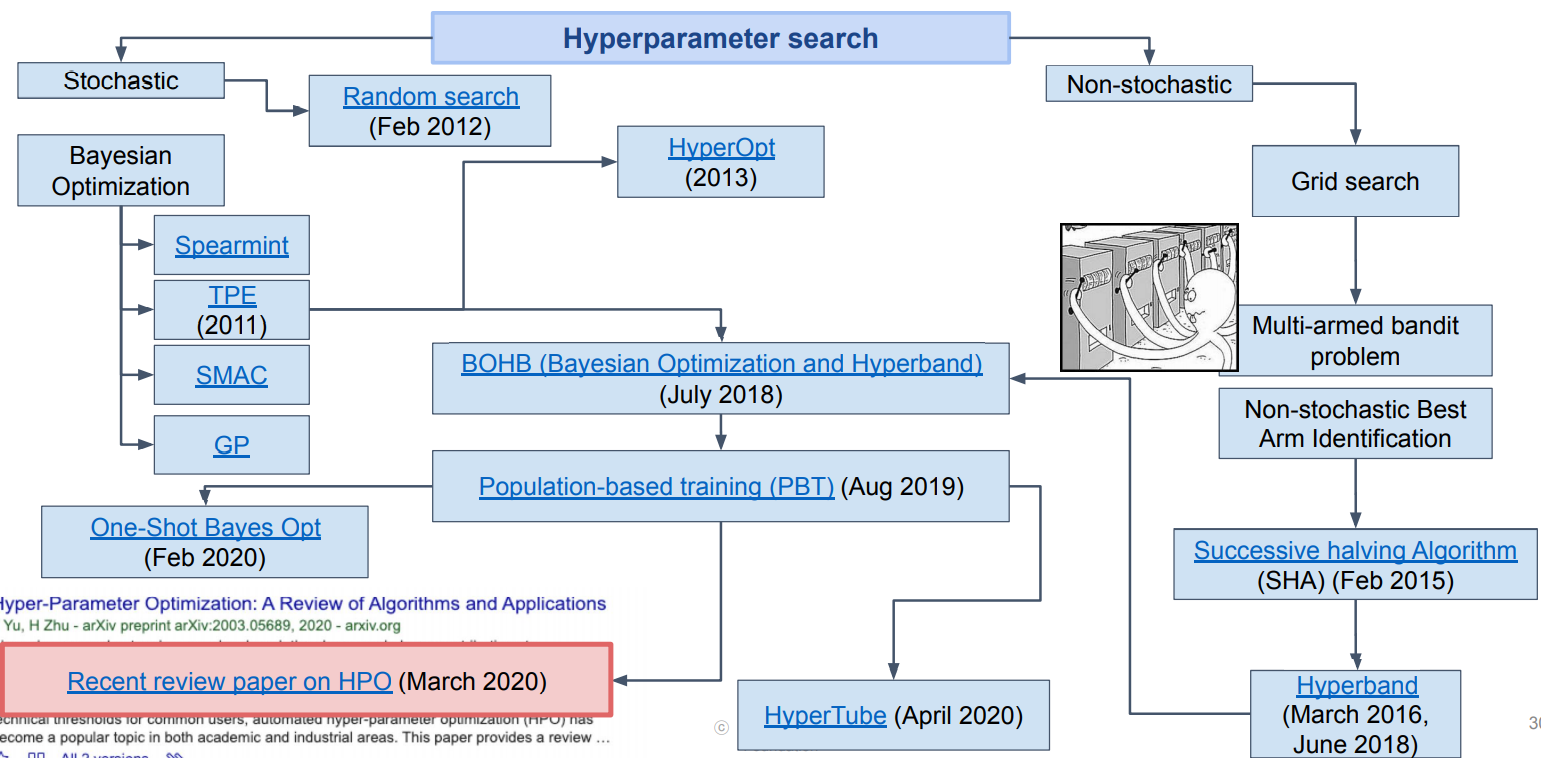
✏️ Neural Architecture Search(NAS)

✏️ NAS For Edge Device

📄 Compression

✏️ Compression rate

✏️

✏️ Encoding

📚 Reference

Algorithm
P=NP?
Information Theory
Cross-entropy
KLD 1
KLD 2
KLD 3

profile
느린 개발자
남들보단 느리지만, 끝을 향해
이전 포스트

[부스트캠프 AI Tech] U-stage. 8-1

다음 포스트

[부스트캠프 AI Tech] U-stage. 8-3

0개의 댓글