[선형대수학] 벡터와 노름

김기정·2024년 4월 22일

Norm vector 벡터 벡터와 노름 선형대수학

선형대수학

목록 보기

1/6

이번 포스팅에서는 벡터(Vector)와 노름(Norm)의 주요 개념에 대해 알아보겠습니다.

Vector

벡터는 크기와 양을 설명하는 스칼라(Scalar)와 방향이 합쳐진 물리량입니다. 예를 들면 속도, 힘, 가속도등이 있습니다. 방향을 뺀 스칼라의 경우에는 거리, 질량이 대표적인 예라 할 수 있습니다.

수학적으로 정의했을 때는 Vector는 Vector Space에 있는 원소라고 할 수 있습니다. 그럼 Vector Space(:벡터공간)에 대한 정의를 알아보겠습니다.

Def> Vector Space

두 가지의 연산이 가능해야 하고 연산에 대한 8개의 공리를 만족시키면 그 집합은 Vector Space라 할 수 있습니다.

Operation : $+$ , $\cdot$
Let $V$ be Set and $F$ be Field.
- vector addition( $+$ ) : $V \times V \rightarrow V$
  Let $\forall v, w \in V$ then $v + w \in V$
- scalar mulitplication( $\cdot$ ) : $F \times V \rightarrow V$
  Let $c$ be scalar and $\forall v \in V$ then $c \cdot v \in V$
Axiom
Let $\forall u, v, w \in V$ and $a, b \in F$ for $V$ : Vector Space & $F$ : Field
[Vector Addition]
- Associativity(결합) : $u + (v + w) = (u +v) + w$
- Commutativity(교환) : $u + v = v + u$
- Identity element(항등원) : there exist $\vec{0} \in V$ such that $u + \vec{0} = \vec{0} + u = u$
- Inverse element(역원) : $\forall v \in V$ , there exist $-v$ such that $v + (-v) = \vec{0}$
[Scalar Multiplication]
- Compatibility : $a(bv) = (ab)v$
- Identity Element : there exist $1 \in F$ such that $1 \cdot v = v$
- Distributivity1 : $a(u + v) = au + av$
- Distributivity2 : $(a + b)u = au + bu

이와 같이 $+, \cdot$ 의 연산이 위의 공리를 만족하면 Vector Space라 한다. 그리고 Vector Space안의 원소를 Vector라 정의합니다.

또한 $F = \R$ 이면 Real Vector Space, $F = \mathbb{C}$ 이면 Complex Vector Space라고 합니다. 저희는 주로 Real Vector Space에 대해서 다루겠습니다.

Example>

$n \in \N$ 에 대해 $\R^n$ 는 Vector Space 이다. ( $\R^3, \R^2, etc$ )
증명과정은 쉽고 간단하기 때문에 증명은 다루지 않겠습니다.

벡터들의 크기를 구하는 방법으로 norm을 사용합니다. 벡터의 크기를 구하는 norm에 대해 알아보겠습니다.

Def> Vector Norm

$||\cdot|| : \R^n \rightarrow \R$

다음 4가지의 조건을 만족시키는 것을 vector norm or norm이라 합니다.

$\forall v \in \R^n, \quad ||v|| \ge 0$
$||v|| = 0 \Leftrightarrow v = \vec{0}$
$\forall a \in \R$ & $\forall v \in \R^n, \quad||av|| = |a|\cdot||v||$
$\forall u, v \in \R^n, \quad ||u + v|| \le ||u|| + ||v||$ : triangle inequality(삼각 부등식)

Norm의 종류는 대표적으로 다음과 같습니다.

For $v \in \R^n$

1 - norm : $||v||_1 = |v_1| + |v_2| + \cdots + |v_n|$
2 - norm : $||v||_2 = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2}$ $\rightarrow$ Euclidean distance(유클리드 거리)
p - norm : $||v||_p = \sqrt[p]{v_1^p + v_2^p + \cdots + v_n^p}$
infinite - norm : $||v||_{\infin} = max\{|v_1|, |v_2|, \cdots, |v_n|\}$

그럼 이제 Norm에 대해 기하학적인 의미를 보겠습니다.

$v = \begin{bmatrix} x \\ y \end{bmatrix} \in \R^2$ 에 대하여, $||v||_1 \le 1,||v||_2 \le 1,||v||_{\infin} \le 1$ 를 색깔별로 구하면 다음과 같습니다.

$||v||_1 \le 1 \quad \Rightarrow \quad |x| + |y| \le 1 \quad \Rightarrow \quad -1 \le x + y \le 1$
$||v||_2 \le 1 \quad \Rightarrow \quad \sqrt{x^2 + y^2} \le 1 \quad \Rightarrow \quad x^2 + y^2 \le 1$
$||v||_\infin \le 1 \quad \Rightarrow \quad max\{|x|, |y|\} \le 1 \quad \Rightarrow \quad |x| \le 1 \ or \ |y| \le 1$

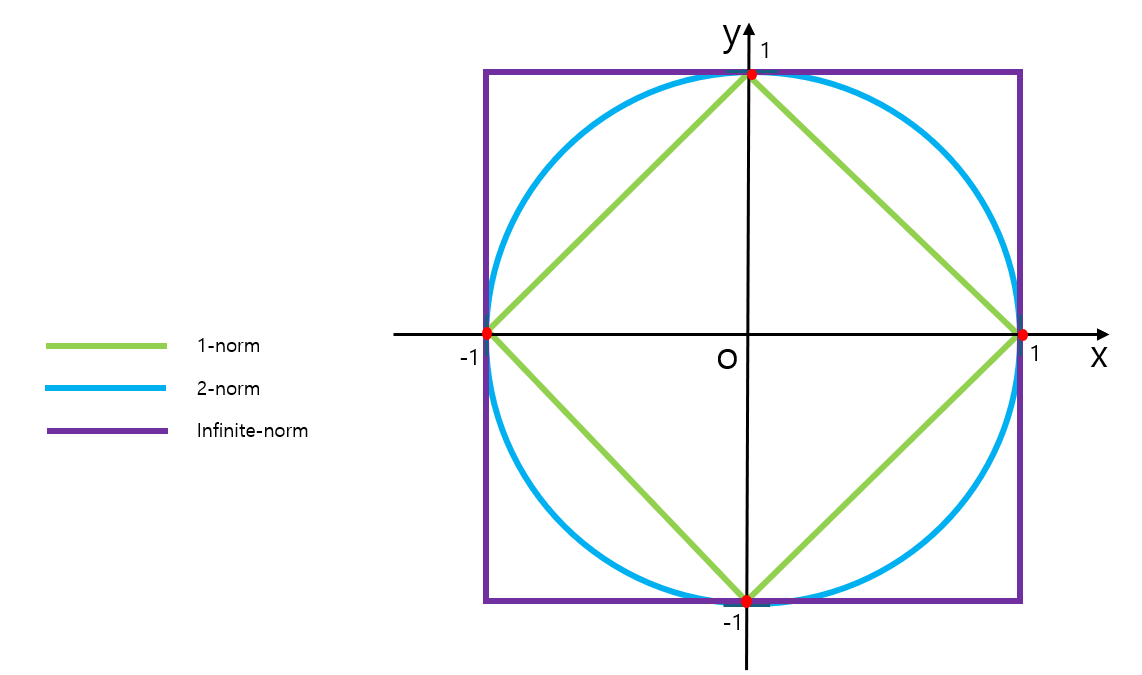
그럼 만약 $v = \begin{bmatrix} 1\\ 1 \end{bmatrix}$ 이라 하면 $||v||_1, ||v||_2, ||v||_\infin$ 의 대수 비교는 어떻게 될까요?

(1) $||v||_1 \le ||v||_2 \le ||v||_\infin$
(2) $||v||_1 \ge ||v||_2 \ge ||v||_\infin$

기하학적인 의미와 반대로 (2)가 정답입니다.

$||v||_1 = 2$
$||v||_2 = \sqrt2$
$||v||_\infin = 1$

전체적으로 대수 비교를 증명하면 다음과 같습니다.

||v||_\infin = |v_{max\_idx}| = \sqrt{v_{max\_idx}^2} \le \sqrt{\sum_{i=1}^n{v_i^2}} = ||v||_2 \\ \text{since } {||v||_2}^2 = \sum_{i=1}^n{v_i^2} \le (\sum_{i=1}^n{|v_i|})^2 = {||v||_1}^2 , \text{we have } ||v||_2 \le ||v||_1 \\

\therefore ||v||_\infin \le ||v||_2 \le ||v||_1

이 노름중에 무엇이 좋다라곤 말할 수 없습니다. 하지만 저는 주로 Euclidean distance인 norm-2를 사용할 예정입니다.

기본 연산

다음으로 Vector의 연산에 대해 다뤄보겠습니다. 저희가 다룰 연산은 $+$ (Addition), Scalar multiplication, $-$ (Subtraction))입니다.

Addition

For $u, v \in \R^n$ ,

u + v \quad = \quad \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} + \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} \quad = \quad \begin{bmatrix} u_1 + v_1 \\ u_2 + v_2 \\ \vdots \\ u_n + v_n \end{bmatrix}

Scalar multiplication

For $c \in \R \quad \& \quad u\in \R^n$ ,

c \cdot u \quad = \quad c \cdot \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} \quad = \quad \begin{bmatrix} c\cdot u_1 \\ c\cdot u_2 \\ \vdots \\ c\cdot u_n \end{bmatrix}

Subtraction

For $u, v \in \R^n$ ,

u - v \quad = \quad u + (-1) \cdot v \quad = \quad \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} + (-1) \cdot \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} \quad = \quad \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} + \begin{bmatrix} -v_1 \\ -v_2 \\ \vdots \\ -v_n \end{bmatrix} \quad = \quad \begin{bmatrix} u_1 - v_1 \\ u_2 - v_2 \\ \vdots \\ u_n - v_n \end{bmatrix}

이처럼 벡터의 연산은 요소별로 연산이 이루어집니다. 다음으로 벡터의 내적에 대해 알아보겠습니다.

벡터의 내적(Inner Product)

벡터의 내적은 다음과 같은 함수입니다.

<\cdot,\cdot> \ : \ V \times V \rightarrow \R \quad (V:\text{Vector Space})

For $u, v \in \R^n$ ,

<u, v> \quad = \quad u^T v \quad = \quad \begin{bmatrix} u_1 & u_2 & \cdots & u_n \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix} \quad = \quad \sum_{i=1}^N{u_iv_i}

벡터의 내적에 대한 정의는 위와 같습니다. 이제 부터는 벡터의 내적에 대한 연산과 관련된 성질에 대해 설명하겠습니다.

Property1. 대칭교환가능

For $u, v \in \R^n$ ,

<u, v> \quad = \quad <v, u>

Property2. scalar multiplication & inner product

For $u, v \in \R^n$ & $c \in \R$ ,

<cu, v> \quad = \quad c <u, v> \quad = \quad <u,cv>

Property3. 분배법칙

For $p,q,r \in \R^n$ ,

<p, q+r> \quad = \quad <p,q> + <p, r>

Property4. 자기 자신과의 내적

For $u \in \R^n$ ,

<u, u> \quad \ge \quad 0 \quad \& \quad <u,u> = 0 \ \Leftrightarrow \ u = \vec0

이렇게 4가지의 성질을 가지고 있습니다. 위 4개의 성질 모두 정의를 이용하면 쉽게 증명이 가능합니다. 이제 부터는 norm과의 관련성, Cauchy-Schwarz inequality, 기하학적인 내적의 의미를 설명드리겠습니다.

1. norm and inner product

For $u \in \R^n$ ,

||u||_2 \quad = \quad \sqrt{\sum_{i=1}^n {u_i}^2 } \quad = \quad \sqrt{<u,u>}

2. Cauchy-Schwarz Inequality

$\forall u, v \in \R^n, \quad |<u, v>| \ \le \ ||u||_2 ||v||_2$

proof>
$\forall u, v \in \R^n \quad \& \quad ||\cdot||_2 = ||\cdot||$ ,

Since definition of norm, we have $||ku +v|| \ge 0. \quad$ So we have $\ \ ||ku +v||^2 \ge 0$ .

\begin{matrix} ||ku+v||^2 &=& <ku+v,ku+v> \\\\ &=& k^2<u,u> + 2k<u,v> + <v,v> \\\\ &=& k^2||u||^2 +2k<u,v> + ||v||^2 \end{matrix}

$D/4$ is discriminant of the quadratic polynomial $ak^2+2bk+c$

\begin{matrix} ||ku+v||^2\quad \ge \quad0 &\Rightarrow& D/4\quad \le \quad0 \\\\ &\Rightarrow& <u,v>^2 - ||u||^2||v||^2 \quad \le\quad 0 \\\\ &\Rightarrow& <u,v>^2\quad \le \quad ||u||^2||v||^2 \\\\ &\Rightarrow& |<u,v>| \quad \le \quad ||u||||v|| \end{matrix}

추가적으로 $|<u, v>|$ 와 $||u||_2||v||_2$ 가 같을 때는 $u,v$ 가 평행하다고 할 수 있습니다. 이유는 다음과 같습니다.

\begin{matrix} |<u, v>| = ||u||||v|| &\Rightarrow& D/4 = 0 &\Rightarrow& ||ku+v||^2 = 0 \\\\ &\Rightarrow& ||ku+v|| = 0 &\Rightarrow& ku+v = \vec0 \\\\ &\Rightarrow& -ku = v &\Rightarrow& u\ //\ v \\\\ \end{matrix}

지금까지 Cauchy-Schwarz inequality에 대해 증명까지 하면서 살펴보았습니다. 마지막으로 내적의 기하학적인 의미에 대해 살펴보겠습니다.

3. 내적이 가지는 기하학적인 의미

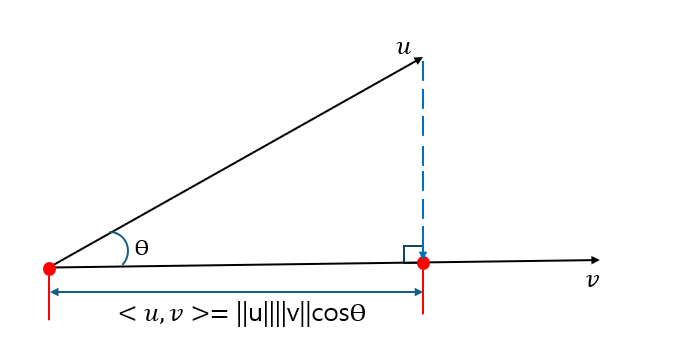
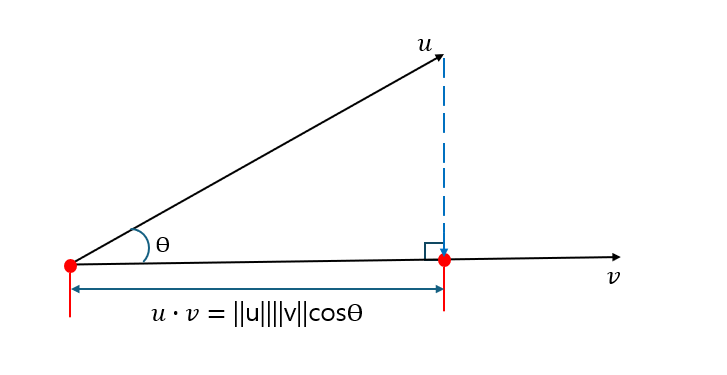
위의 그림을 보면 $<u,v>$ 를 기하학적으로 표현한 식입니다. 주목해야 할 것은 $\cos\theta$ 입니다.

코사인 법칙을 이용해 $\cos\theta = {<u,v>\over ||u||||v||}$ 이라는 점을 구할 수 있습니다.

또한 Cauchy-Schwarz inequality와도 관련성이 있습니다.

|<u,v>| \ \le \ ||u||||v|| \ \Rightarrow \ |{<u,v>\over ||u||||v||}| \ \le \ 1 \ \Rightarrow \ -1 \ \le \ {<u,v>\over ||u||||v||} \ \le \ 1 \\\\

즉, $\theta$ 에 따라 내적의 값에 영향을 받습니다. 만약 $\theta ={\pi \over2}$ 라면 $\cos\theta = 0$ 이 되어 내적 또한 0이 되어버립니다. 기하학적인 의미는 여기까지 입니다.

이번 포스팅은 여기서 마치겠습니다. 궁금한점이나 잘못된점이 있으면 댓글 달아주시면 감사하겠습니다.

Reference

김기정

끊임 없이 도전하는 개발자입니다.

다음 포스트

[선형대수학] 벡터와 노름