[머신러닝 인강] 6. 회귀분석(5)

회귀분석

회귀분석이란

• 지도 학습(supervised learning)
  $Y = f(X)$에 대하여 입력 변수(X)와 출력변수 (Y)의 관계에 대하여 모델링하는것(Y에 대하여 예측 또는 분류하는 문제
  • 회귀(regression): 입력변수 X에 대해서 연속형 출력 변수 Y를 예측
  • 분류(classification): 입력변수 X에 대해서 이산형 출력 변수 Y(class)를 예측

• 회귀분석
  • 입력 변수인 X의 정보를 활용하여 출력 변수인 Y를 예측하는 방법
  • 회귀분석 중 간단한 방법으로는 선형회귀분석이 있으며, 이를 바탕으로 더 복잡한 회귀분석이 개발

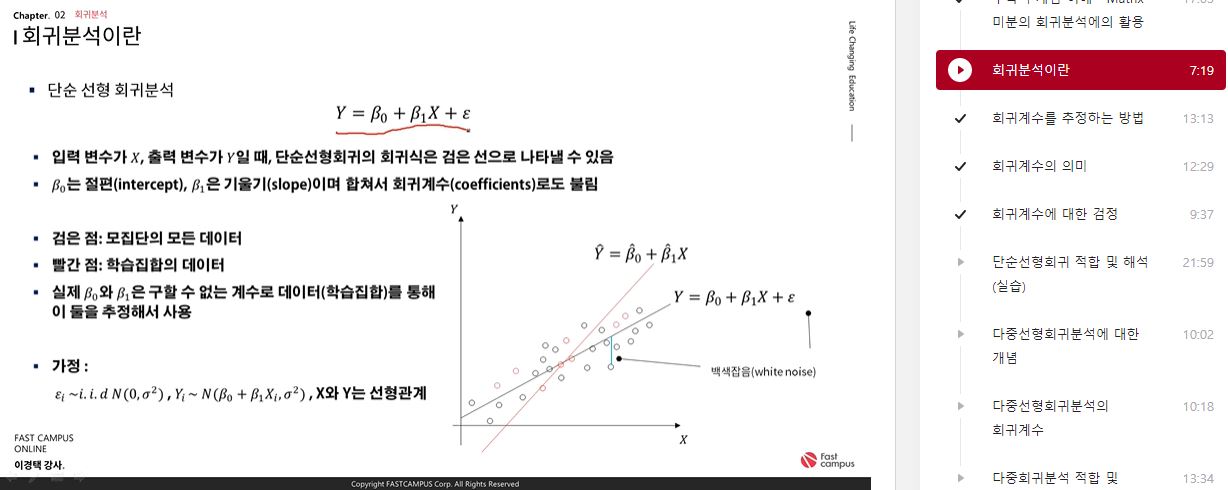
• 단순 선형 회귀분석
  $Y = \beta_0 + \beta_1X + \epsilon$

• $\beta_0$는 절편(intercept), $\beta_1$은 기울기(slop)이며 합쳐서 회귀계수(coefficients)로도 불림

• 실제 $\beta_0$와 $\beta_1$은 구할 수 없는 계수로 데이터(학습집합)를 통해 이 둘을 추정해서 사용

• 단순 선형 회귀분석
  • 우리가 알고 싶은 식
    $Y = \beta_0 + \beta_1X + \epsilon$
  • 우리가 추정 해야하는 식
    $\hat{Y} = \hat{\beta_0} + \hat{\beta_1}X$
  • 어떻게 추정 할까?
    • 여러 개의 직선 중 가장 좋은 직선은?
      $\rightarrow$ 직선과 데이터의 차이가 평균적으로 가장 작아지는 직선

회귀계수 추정

• 어떻게 추정 할까?
  • 실제 값과 우리가 추정한 값이 차이가 적으면 적을 수록 좋을 것
    $e_i = y_i - \hat{y}_i$
  • 실제 값과 우리가 추정한 값의 차이를 잔차(residual)라고 하면 이를 최소화 하는 방향으로 추정

• 잔차의 제곱합(SSE; Error Sum of Squares)는 아래와 같이 표현 가능
  $SSE = \sum_{i=1}^n e_i^2 = e_1^2+e_2^2+\cdots+e_n^2$

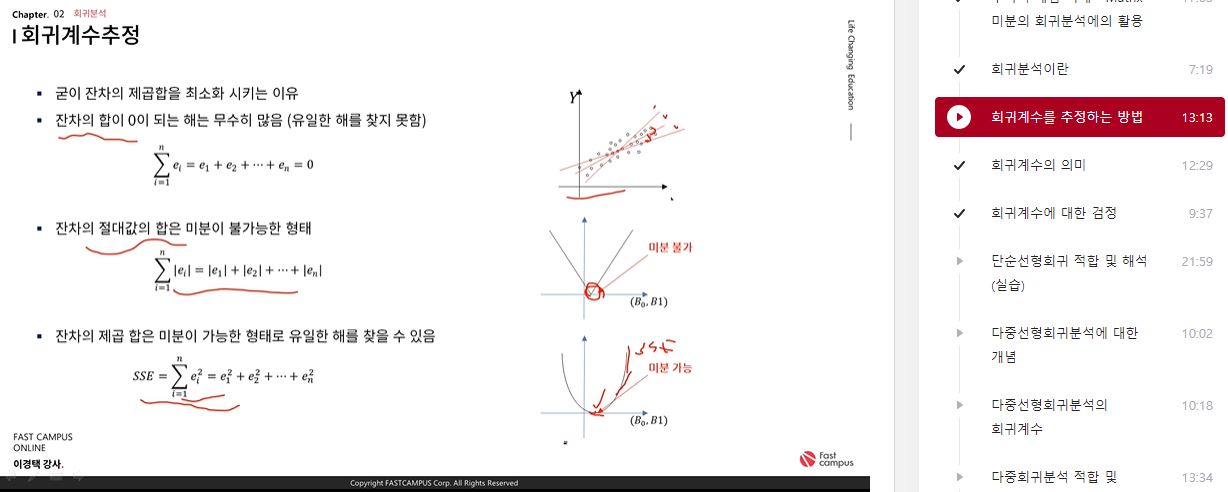
• 굳이 잔차의 제곱합을 최소화 시키는 이유
• 잔차의 합이 0이 되는 해는 무수히 많음(유일한 해를 찾지 못함)
• 잔차의 절댓값의 합은 미분이 불가능한 형태
• 잔차의 제곱 합은 미분이 가능한 형태로 유일한 해를 찾을 수 있음

회귀 계수의 추정

• SSE $\hat{\beta}_0$과 $\hat{\beta}_1$로 편미분하여 연립방정식을 푸는 방법(Least Square Method)

SSE = $\sum_{i=1}^n e_i^2 = \sum_{i=1}^n(y_i-\beta_0-\beta_1x_1)^2$

${\delta L \over \delta \beta_0} = -2\sum_{i=1}^n(y_i-\beta_0-\beta_1x_i) = 0$

${\delta L \over \delta \beta_1} = -2\sum_{i=1}^n(y_i-\beta_0-\beta_1x_i)x_i = 0$

$\hat{\beta}_1 = {\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) \over \sum_{i=1}^n(x_i-\bar{x})^2}$

$\hat{\beta}_0 = \bar{y}-\hat{\beta}_1\bar{x}$

회귀계수의 의미

• 회귀계수의 해석
  • $\hat{\beta}_1$의 해석 - X1이 1증가할 때 마다 y가 $\hat{\beta}_1$만큼 증가한다

• 선형 회귀의 정확도 평가

  • 선형회귀는 잔차의 제곱합(SSE : Error sum of squares)를 최소화 하는 방법으로 회귀 계수를 추정
  • 즉, SSE가 작으면 작을수록 좋은 모델이라고 볼 수 있음
  • MSE(Mean Squared Error)는 SSE를 표준화한 개념
    $SSE = \sum_{i=1}^n(y_i-\hat{y}_i)^2$
  $MSE = {1 \over n-2}SSE$
  $SST = SSE + SSR$
  $\sum_{i=1}^n(y_i-\bar{y})^2 = \sum_{i=1}^n(y_i-\hat{y})^2 + \sum_{i=1}^n(\hat{y_i}-\bar{y})^2$
  • Y의 총 변동은 회귀직선으로 설명 불가능 한 변동과 회귀직선으로 설명 가능한 변동으로 이루어져 있음
  • $R^2$는 RSE의 단점을 보완한 평가지표로 0~1의 범위를 가짐
  • $R^2$은 설명력으로 입력 변수인 X로 설명할 수 있는 Y의 변동을 의미
  • $R^2$이 1에 가까울 수록 선형회귀 모형이 설명력이 높다는 것을 뜻함
    $R^2 = {SST - SSR \over SST} = 1 - {SSE \over SST} = {SSR \over SST}$
  • 회귀 분석은 결국 Y의 변동성을 얼마나 독립변수가 잘 설명하느냐가 중요
  • 변수가 여려 개일 때 각각 Y를 설명하는 변동성이 크면 좋은 변수 -> p-value자연스레 낮아짐

회귀계수에 대한 검정

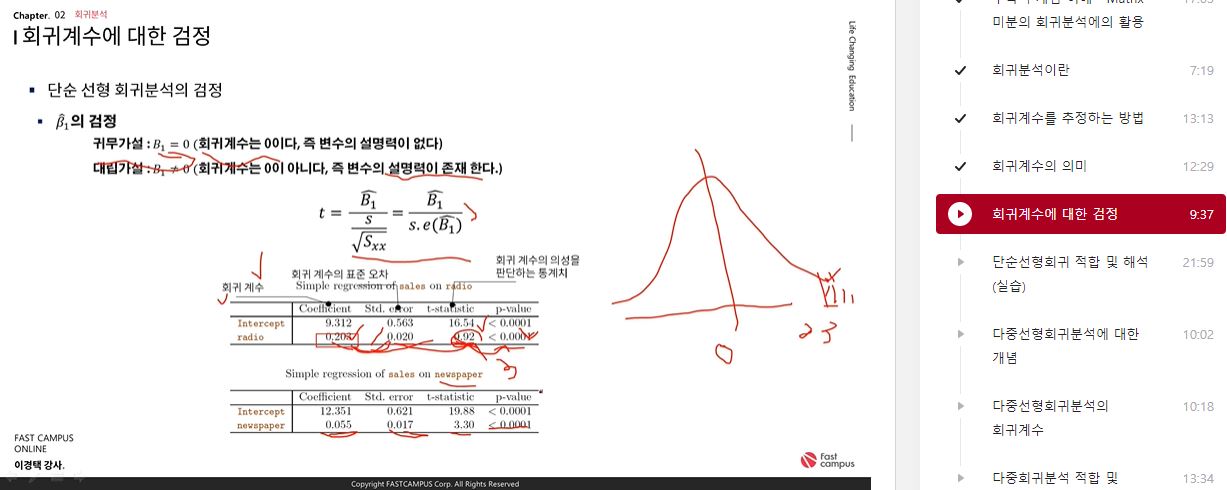
• 단순 선형 회귀분석의 검정
  • $\hat{\beta}_1$의 표준오차
    $S.E(\hat{\beta_1}) = {\sigma \over \sqrt{S_{xx}}}$
    오차의 표준편차가 알려져 있지 않은 경우, $s = \sqrt{SSE \over n-2}$를 대입하여 추정
  • $\hat{\beta}_1$의 표본분포
    $t = {(\hat{\beta_1}-\beta_1) \over {s \over \sqrt{S_{xx}}}} \sim t(n-2)$
  • $\hat{\beta}_1$의 검정
    • 귀무가설: $B_1 = 0$(회귀계수는 0이다, 즉 변수의 설명력이없다)
    • 대립가설: $B_1 \ne 0$(회귀계수는 0이 아니다, 즉 변수의 설명력이 존재 한다)
  • $\hat{\beta}_1$의 신뢰구간
    • $B_1$의 100(1-a)%신뢰구간: $\hat{B_1} \pm t_{a \over 2}(n-2)\times{s \over \sqrt{S_{xx}}}$
  • $\hat{\beta}_0$의 신뢰구간
    • $B_0$의 100(1-a)%신뢰구간: $\hat{B_0} \pm t_{a \over 2}(n-2)\times s \sqrt{{1 \over n} + {\bar{x}^2 \over S_{xx}}}$

머신러닝과 데이터 분석 A-Z 올인원 패키지 Online. 👉 https://bit.ly/3cB3C8y