[머신러닝 인강] 6. 회귀분석(6)

Uno·2021년 5월 15일

패스트캠퍼스 머신러닝과 데이터 분석

목록 보기

26/27

단순선형회귀분석 실습

import os
import pandas as pd 
import numpy as np
import statsmodels.api as sm

# 데이터 불러오기
boston = pd.read_csv("../Data/part2_data/Boston_house.csv")

boston_data = boston.drop(['Target'],axis=1)
# boston_data

boston_data.describe()

crim/rm/lstat 세 개의 변수로 각각 단순 선형 회귀 분석하기

target = boston[['Target']]
# boston_target
crim=boston[['CRIM']]
rm=boston[['RM']]
lstat=boston['LSTAT']

target ~ crim 선형회귀분석

crim1 = sm.add_constant(crim, has_constant='add')

model1 = sm.OLS(target,crim1)
fitted_model1=model1.fit()

fitted_model1.summary()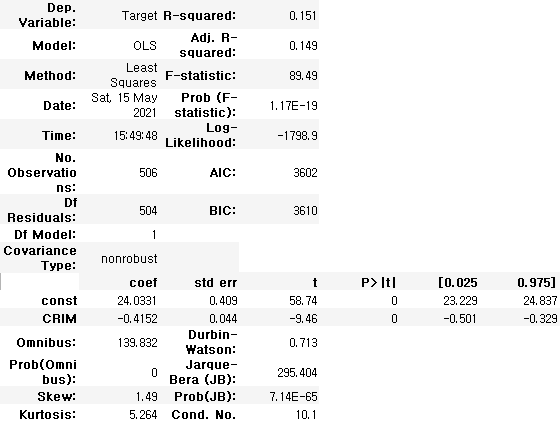

y_hat = beta0 + veta1 * X 계산해보기

np.dot(crim1,fitted_model1.params)

>>>
array([ 24.03048217,  24.02176733,  24.02177563,  24.01966646,
        24.00443729,  24.02071274,  23.99644902,  23.97309042,
        23.94540138,  23.96250722,  23.93973403,  23.98433377,
        23.99416963,  23.77163594,  23.76823138,  23.77261995,
        23.59552468,  23.70751396,  23.69982879,  23.73176107,
        23.51337514,  23.67934745,  23.52139661,  23.62271965,
        23.72160552,  23.68412214,  23.75413567,  23.63627976,
        23.71216824,  23.61689868,  23.56360486,  23.4706396 ,
        23.45682622,  23.55492323,  23.36347899,  24.00646341,
        23.99265003,  23.99983283,  23.96042712,  24.02163447,
        24.01915993,  23.98019433,  23.97435675,  23.96694145,
        23.98216648,  23.96193426,  23.95490093,  23.9379155 ,
        23.92770182,  23.94185981,  23.99626634,  24.01509937,
        24.01085198,  24.01242555,  24.02745959,  24.02766303,
        24.02457401,  24.02716065,  23.96898004,  23.99022532,
        23.97110996,  23.96181385,  23.98732314,  23.9805846 ,
        24.02500581,  24.01822575,  24.01492499,  24.00907081,
        23.97683128,  23.97989539,  23.99646148,  23.96719057,
        23.99505814,  23.95198215,  24.00032275,  23.99361327,
        23.99095191,  23.99695556,  24.00966453,  23.99828417,
        24.0160294 ,  24.01458038,  24.01791436,  24.01836277,
        24.0121017 ,  24.00929501,  24.0115661 ,  24.00341592,
        24.0096064 ,  24.01109279,  24.01365866,  24.01678089,
        24.01565573,  24.02116945,  24.0152779 ,  23.98243635,
        23.98534268,  23.98293873,  23.99911455,  24.00462412,
        23.97138399,  23.98564162,  23.93812725,  23.94524776,
        23.97514561,  23.97804364,  23.9620256 ,  23.97864567,
        23.97995351,  23.92364956,  23.98829469,  23.99123839,
        23.98191736,  23.94088411,  23.97402045,  23.96196747,
        23.97847544,  23.97042075,  23.97889063,  23.97300323,
        24.0044622 ,  24.00335779,  23.99449763,  23.97066986,
        23.99221408,  23.96293071,  23.87228222,  23.92550961,
        23.8979908 ,  23.66721974,  23.89191657,  23.53780908,
        23.78812315,  23.89616812,  23.62780988,  23.80152134,
        23.89914918,  23.88682218,  23.92939164,  23.80702676,
        23.91232732,  23.35691068,  22.6542385 ,  22.33190553,
        22.87898515,  23.04522734,  23.13835037,  23.04967818,
        23.06530179,  22.89798841,  23.34530196,  23.41184866,
        23.56536111,  23.14078753,  23.4460894 ,  22.56540439,
        23.01726842,  23.52508765,  23.47557206,  23.44145172,
        23.50437796,  23.42553333,  23.2717427 ,  23.40242384,
        23.1021001 ,  22.8190898 ,  23.19849483,  23.28564742,
        23.07800246,  23.01608513,  23.53179713,  23.07239739,
        23.9753366 ,  23.99500001,  23.99803505,  24.00543789,
        24.00395151,  24.0105821 ,  24.00552924,  24.00910818,
        24.00575344,  24.00450787,  23.9953114 ,  23.99155393,
        23.99861217,  24.00799962,  24.00984721,  24.00040994,
        23.98087939,  23.99835475,  23.99545672,  24.00441237,
        23.99713409,  24.02402596,  24.02713159,  24.0273724 ,
        24.01645289,  24.0137334 ,  24.0174618 ,  24.02002768,
        24.02572409,  24.01880287,  24.02406748,  24.018533  ,
        24.024765  ,  23.97646592,  23.93774112,  23.92848238,
        23.97669427,  23.85220362,  23.96067208,  23.87708597,
        23.942931  ,  23.97476364,  23.91288783,  23.9508902 ,
        24.0141735 ,  24.00398888,  23.98714876,  23.98567068,
        23.88443069,  23.86382895,  23.77421012,  23.77788871,
        23.90218422,  23.81432996,  23.87444536,  23.86189001,
        23.90930059,  23.84968341,  23.81014899,  23.84088968,
        23.79425136,  23.89548305,  23.8471383 ,  23.89590655,
        23.81696642,  23.82059933,  23.99887789,  23.99469277,
        23.98606927,  23.98904618,  23.99038309,  23.98014035,
        23.94754376,  23.95366782,  23.89201206,  23.95149222,
        23.96485304,  23.95391693,  23.97485498,  23.94421809,
        23.99897338,  23.87992587,  24.01309815,  24.01837522,
        24.02672055,  23.77920071,  23.75762327,  23.76047148,
        23.80885775,  23.81134474,  23.8171491 ,  23.69046625,
        23.80472246,  23.71688895,  23.70689117,  23.79298503,
        23.80869583,  23.99546918,  23.90889785,  23.96579968,
        23.98552537,  23.94098376,  24.00967283,  23.9932313 ,
        23.9896399 ,  24.00766747,  23.99998229,  23.94575844,
        24.01825067,  24.01772337,  24.00765916,  24.02687417,
        24.02934455,  24.02855569,  24.02494769,  24.01703416,
        24.01404894,  24.01526545,  24.01856621,  24.00036427,
        24.01809705,  23.9987907 ,  23.99906472,  23.97941377,
        24.01080215,  23.97455189,  24.00625997,  24.01001744,
        24.01476722,  24.01842089,  23.99463464,  23.99158715,
        24.01020843,  24.0103579 ,  24.00195445,  24.01262899,
        23.82842567,  23.88803869,  22.9388805 ,  23.70493563,
        23.92445503,  23.92126222,  23.87981792,  23.92783053,
        23.90096356,  23.93129321,  23.86619138,  23.83569565,
        23.96352028,  23.95771177,  23.88731626,  23.91522535,
        23.89148892,  23.95344777,  23.90710838,  23.93303286,
        24.00563303,  24.00518878,  24.01423993,  24.01225117,
        24.01871568,  24.01200205,  24.01758636,  24.01666049,
        24.0188776 ,  24.02048024,  24.01937998,  24.01028316,
        24.00756782,  24.02770455,  24.02273472,  24.02254789,
        24.02044702,  24.0201813 ,  24.00752215,  24.02534212,
        24.02687417,  24.02106981,  24.00731871,  24.00009855,
        24.00302979,  24.02601057,  24.01524884,  23.98885104,
        20.30346852,  22.43474816,  21.87338184,  22.26385169,
        22.14734515,  22.44008751,  22.50594499,  22.2800109 ,
        22.5906189 ,  22.14155324,  22.49816848,  18.4188202 ,
        21.99941285,  21.6789856 ,  21.31827659,  20.19994497,
        20.60062435,  19.42113105,  16.35283338,  15.8915985 ,
        17.68567721,  19.95448863,  14.21460344,  16.61502604,
       -12.90894703,  17.44220963,  20.21874479,  20.71470618,
        15.69405096,  17.05301026,  13.90503757,  14.65100995,
        18.08189329,  20.64858298,  21.14248918,  21.83548327,
        19.22607466,  20.44388587,  18.4862471 ,  20.41399632,
        21.5950881 ,  20.84775806,   8.10981167,  19.91585102,
        13.63420895,  18.12237434,  20.04906067,  13.73568146,
         6.79058608,  -4.16694965,  15.43194134,  19.07112564,
        20.95908303,  18.03846438,   2.80201916,  18.19939214,
        16.22296186,  12.13549661,   5.0397702 ,  16.52455607,
        19.53485167,  13.26282125,  -6.49753724,  19.12875405,
        19.42972549,  21.11739508,  19.03081067,  21.10584033,
        20.38270343,  17.44806381,  18.9481878 ,   8.39625145,
        20.97435373,  20.15568984,  20.50725636,  19.85533704,
        21.35759926,  21.71590017,  18.25639776,  19.3994166 ,
        18.04573021,  17.73168029,  18.35409203,  20.13420789,
        14.87770384,  19.99572118,  21.68048444,  19.89509566,
        18.71771568,  19.60227857,  21.42236064,  19.91240494,
        20.1597587 ,  20.90837999,  21.24397414,  21.77399775,
        21.91971708,  20.60857939,  20.08313949,  22.05996835,
        22.09465335,  20.62830508,  20.81445565,  21.20932651,
        22.03515658,  22.49976281,  21.27004809,  21.61622129,
        20.77829672,  22.71961021,  22.46577118,  22.19701851,
        17.56622696,  18.60445177,  22.22753085,  22.3563976 ,
        22.55142493,  22.10376262,  20.68842049,  21.3787449 ,
        22.0105441 ,  17.79553655,  19.78446406,  18.08189329,
        21.61503384,  21.66312533,  21.65358426,  22.8629422 ,
        23.04554703,  22.50783411,  21.66994691,  22.025383  ,
        23.97047057,  23.95697273,  23.9469708 ,  23.98920395,
        23.98688719,  23.96114955,  23.91703143,  23.95879127,
        23.91286707,  23.92167741,  23.93382587,  23.95927289,
        23.93994578,  24.00710281,  24.01431051,  24.00787921,
        23.98760547,  24.013422  ])

len(np.dot(crim1,fitted_model1.params))
>>> 506

pred1=fitted_model1.predict(crim1)

pred1-np.dot(crim1,fitted_model1.params)

>>> 0      0.0
    1      0.0
    2      0.0
    3      0.0
    4      0.0
          ... 
    501    0.0
    502    0.0
    503    0.0
    504    0.0
    505    0.0
    Length: 506, dtype: float64

적합시킨 직선 시각화

import matplotlib.pyplot as plt
plt.yticks(fontname = "Arial") #
plt.scatter(crim,target,label="data")
plt.plot(crim,pred1,label="result")
plt.legend()
plt.show()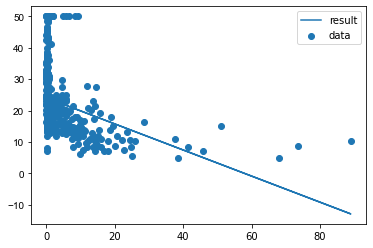

plt.scatter(target,pred1)
plt.xlabel("real_value")
plt.ylabel("pred_value")
plt.show()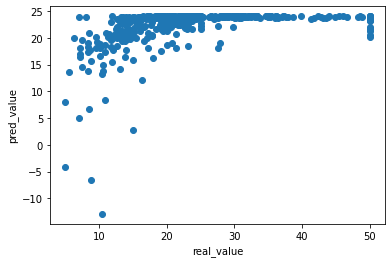

fitted_model1.resid.plot()
plt.xlabel("residual_number")
plt.show()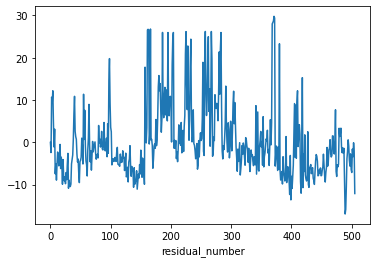

##잔차의 합계산해보기
sum(fitted_model1.resid)

>>> -3.693045869113121e-12

위와 동일하게 rm변수와 lstat 변수로 각각 단순선형회귀분석 적합시켜보기

rm1 = sm.add_constant(rm, has_constant='add')
lstat1 = sm.add_constant(lstat, has_constant='add')

model2 = sm.OLS(target,rm1)
fitted_model2=model2.fit()
model3 = sm.OLS(target,lstat1)
fitted_model3=model3.fit()

fitted_model2.summary()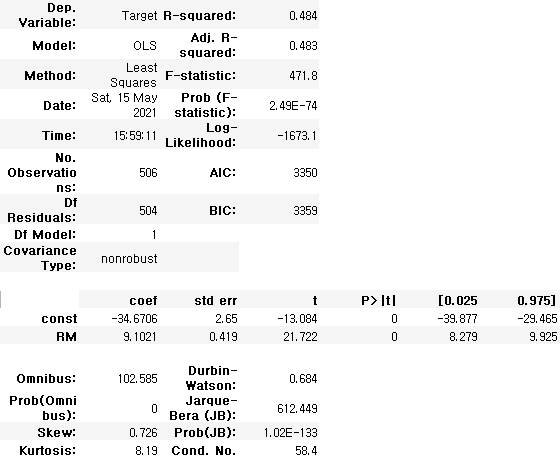

fitted_model3.summary()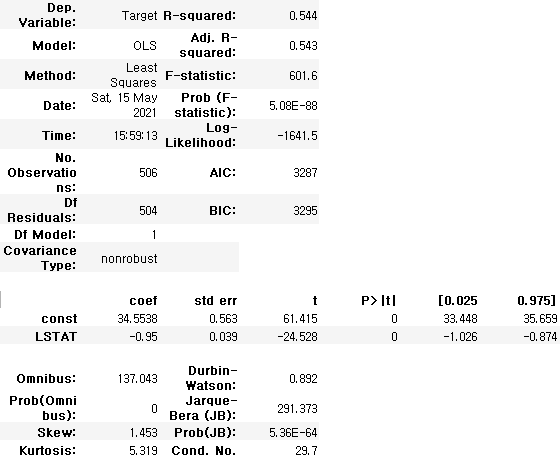

pred2=fitted_model2.predict(rm1)
pred3=fitted_model3.predict(lstat1)

import matplotlib.pyplot as plt
plt.scatter(rm,target,label="data")
plt.plot(rm,pred2,label="result")
plt.legend()
plt.show()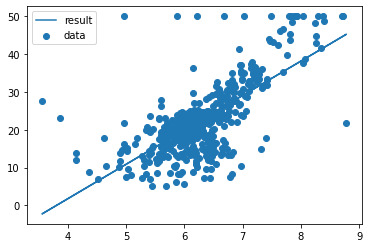

import matplotlib.pyplot as plt
plt.scatter(lstat,target,label="data")
plt.plot(lstat,pred3,label="result")
plt.legend()
plt.show()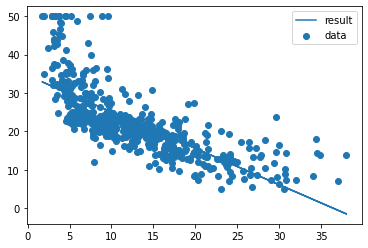

fitted_model2.resid.plot()
plt.xlabel("residual_number")
plt.show()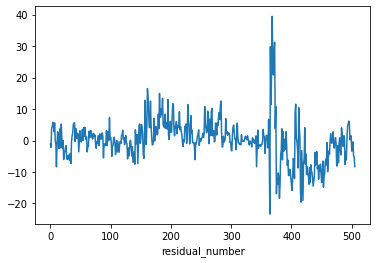

fitted_model3.resid.plot()
plt.xlabel("residual_number")
plt.show()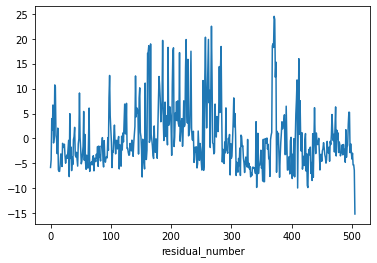

fitted_model1.resid.plot(label="crim")
fitted_model2.resid.plot(label="rm")
fitted_model3.resid.plot(label="lstat")
plt.legend()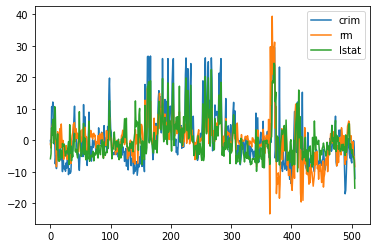

다중회귀분석에 대한 개념

다중 선형 회귀분석

단순 선형 회귀분석: 변수가 1개인 경우 $\hat{Y} = \hat{\beta}_0 + \hat{\beta}_1X$
다중 선형 회귀분석: 변수가 여러개인 경우 $\hat{Y} = \hat{\beta}_0 + \hat{\beta}_1X_1 + \hat{\beta}_2X_2 + \cdots + \hat{\beta}_pX_p$
다중 선형 회귀계수 추정
- 회귀계수를 추정하는것은 단순선형회귀분석과 동일하게 SSE를 최소화 하는 방향으로 추정 $SSE = \sum_{i=1}^n e_i^2 = e_1^2 + e_2^2 + \cdots + e_n^2$
위 식을 각각의 변수에 대해 편미분 하여 회귀계수를 추정

다중회귀분석에 회귀계수

다중 선형 회귀분석

다중 선형 회귀 계수 검정
- $\hat{\beta}_p$ 의 검정
  - 귀무가설: $B_p = 0$ (회귀계수는 0이다, 즉 변수의 설명력이 없다)
  - 대립가설: $B_p \ne 0$ (회귀계수는 0이 아니다, 즉 변수의 설명력이 존재 한다) $t = {\hat{B_p} \over {s \over \sqrt{S_{xx}}}} = {\hat{B_p} \over s.e(\hat{B_p})}$

다중 선형 회귀 모델 검정
- 귀무가설: $B_1 = B_2 \dots B_p = 0$ (모든 회귀계수는 0이다, 즉 변수의 설명력이 하나도 존재 하지 않는다)
- 대립가설: 하나의 회귀계수라도 0이 아니다(즉 설명력이 있는 변수가 존재 한다)
- F검정을 통해서 검정
  $F = {V_1/k_1 \over V_2/k_2} \sim F(k_1,k_2)$
  - 두 확률 변수 V1,V2가 독립인 카이제곱 분포를 따른다고 할 때, 확률 변수 F는 F분포를 따른다고 한다. F검정과 분산분석등에서 주로 사용됨