.png)
.png)
Abstract
-
The idea
: discriminate between observed data and generated noise
: using regression model -
Estimatior
: consistent of estimators , asymptotic variance
: works for unnormalized model -> necessary to learn normalize constant
- Experiment setup
: ICA model – s= Wx -> s,x가 주어지고 W를 찾는 것
: comparing with unnormalized model
ex) score matching, contrastive divergence and maximum likelihood with importance sampling
introduction
NCE
: for estimating probability density function(pdf) with theta
: for unnormalized model
: connection between unsupervised and supervised
: input - data x and noise y (contrasted data)
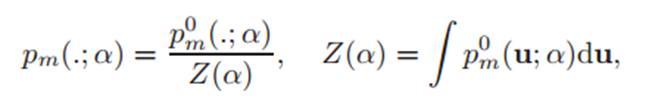
-> MLE로 추정 불가능( 단순 모델을 찾는게 아닌 Z만 줄이면 되어서)
Noise-contrastive estimation
- 2-1 define the estimator
: pdf
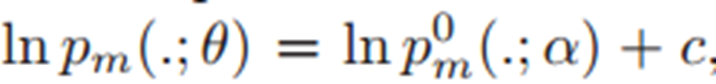
: objective function to optimize
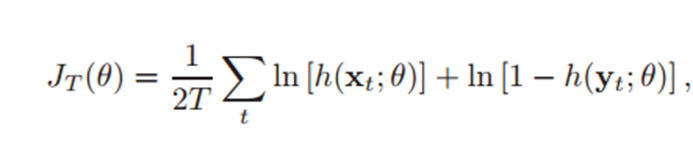
-> h는 regression function with sigmoid
- 2-2 connection to supervised
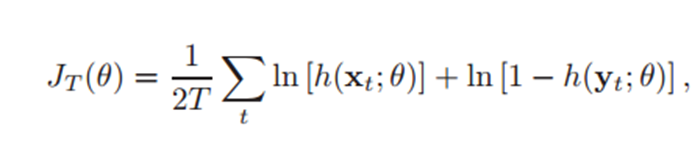
: by comparing between data and noise, we can learn properties of the data in the form of a statistical model
-> learning by comparison
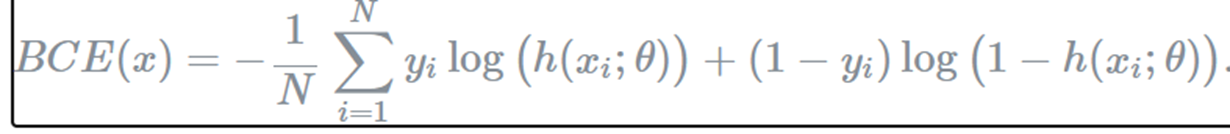
-> - 떼면 objective 됨.
- 2-3 properties of the estimator
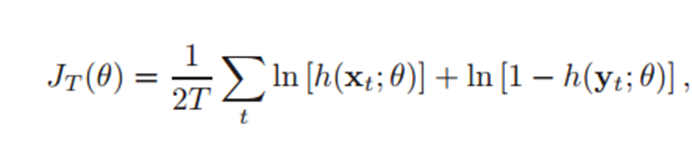
-> MLE나 NSE의 가정은 학습을 하면 수렴할 것이다. [T가 크면]
*** 3 theorem
1. J는 특정 모델에서 최대화 될 것이다.
2. 모델의 파라미터는 특정값으로 수렴한다.
3. 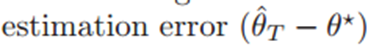 -> 요식은 다중 정규분포를 따를 것이다.
-> 요식은 다중 정규분포를 따를 것이다.
*** theorem1 : J는 특정 모델에서 최대화 될 것이다.
: our model need not to be normalized
: 대신 모델이 모든 x에서 잘 정의되어야 한다.(가우시안 정규분포)
: T는 충분히 커야 local minima 안 빠진다.
*** theorem2 : 모델의 파라미터는 특정값으로 수렴한다.
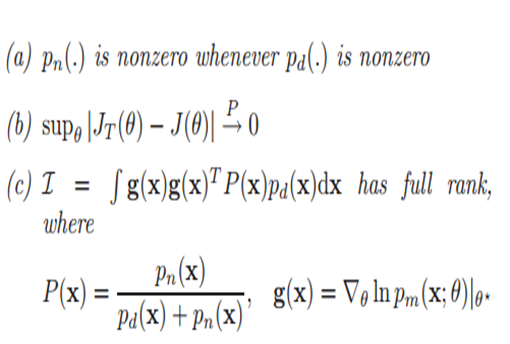
수렴 조건을 위해 만족해야 할 3가지
1. 모든 x에서 정의되어야 한다.
2. J의 수렴점이 존재해야 한다.
여기까지만 만족하면하면 세타가 매우 많음
-> 3. 수렴점이 단 하나여야 한다.
-C를 이해 못할 것이라 여깁니다.
: I는 피셔 정보량 혹은 각 x데이터마다 분포 추정하고 그들의
기울기 상관관계행렬(분산으로 받아들이세요..)
= MLE를 두 번 미분한 값 -> x가 모수에 대해 줄 수 있는 정보량
: 즉 분포에서 기울기가 급격하게 변화하냐 완만하게 변화하냐
-» 피셔정보량이 크다 – 이계도 함수가 작다 – 봉우리가 뾰족
하다 -> 봉우리를 찾기가 쉬워진다.
: 근데 여기서 full rank여야 하는 이유 -> inverse를 구해야 하기 때문이다.
->> 왜 inverse를 구하느냐? 그것은 우리가 구하려는 model 추정치의 최저한도를 설정할 수 있음 -> 크레머 라오 lower bound라고 부르는 이것이 있어야 모델의 특정 점으로 수렴함을 보장할 수 있음
->> 또 다른 해석 세타로 미분한 값들이 서로 상관관계가 있다면 세타는 유일하지 않다. -> 수렴 점이 매우 많아진다.
*** theorem3 : 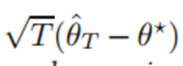
다중 정규분포(0,공분산)를 따를 것이다.
: 샘플표본평균 분산 : sigma^2/T -> 표준편차
: 추정 세타는 특정 범위 내에서 수렴해서 존재할 것이다.
: T가 충분히 크다면 MSE는 tr(sigma)/T이다. -> T가 크면 에러는 충분히 작아진다.
- 2-4 choice of the contrastive noise distribution
*conditions
: easy to sample
: log처리가 쉬움
: 추정세타와 모집단 세타간의 구분이 잘 되어야 함
-> 그러나 보통 noise distribution을 잘 학습한다는 것은 어렵다고 논문에서 표현 그래서 1,2번째 중심으로 distribution 선택
: 직관적으로 우리가 구분하기 힘든 data를 가져와야 학습하는 의미가 있음
: 따라서 데이터와 비슷하지만 다른 것들을 노이즈로 삼기
: 수식적으로 이스티메이터의 에러 하한치가 노이즈와 가까울 수록 두배 정도 줄어듬
: 그래서 같은 모델을 쓰는 것이 contrastive loss에서 많이 사용되는 것인듯 보임
Simulations
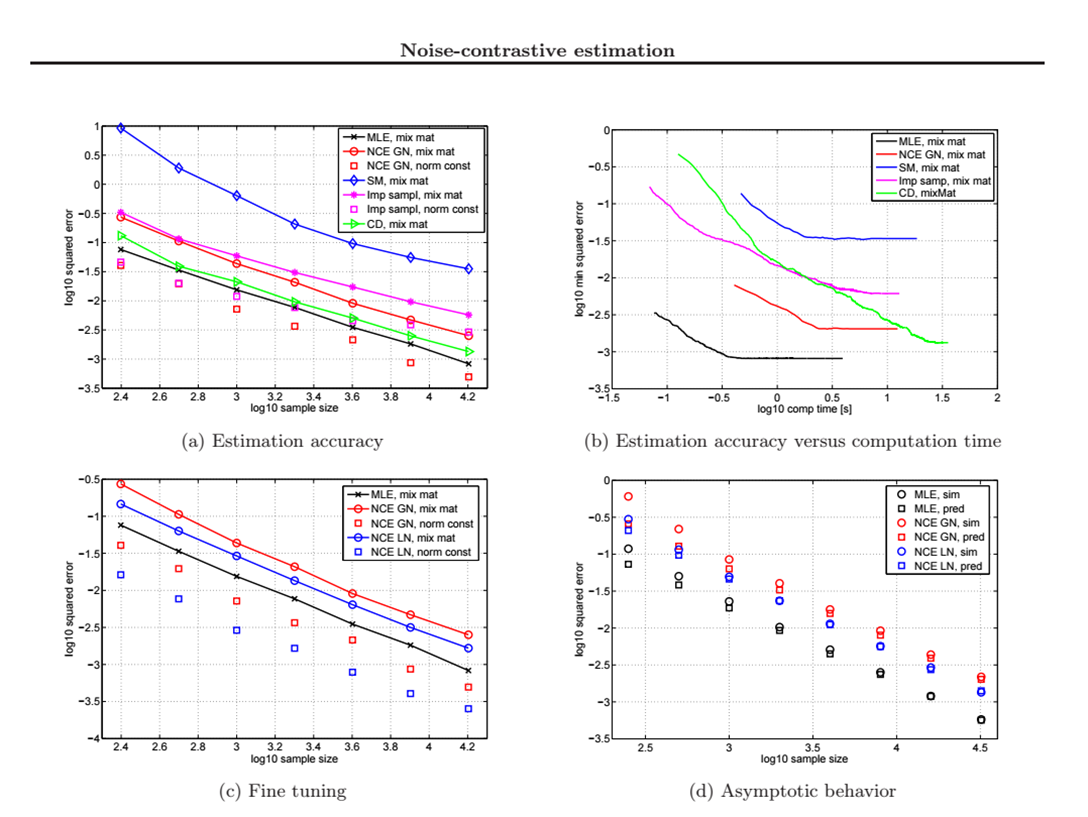
Results
: mix mat – normal
: norm const – unnormal
: a,b에서 MLE 빼고
Unnormalized method
: c는 가우시안으로 학습 후
라플라시안으로 학습
Results
: NCE가 MLE를 제외하고 학습속도
제일 빠름
: NCE가 unnormalized에서 top
Conclusion
NCE에서 정규화 상수 또한 추정가능하다.