파이썬 라이브러리를 이용해 알고리즘의 성능을 비교해보는 프로젝트를 진행해보자.
비교할 알고리즘은 A* 알고리즘과 BFS 알고리즘이다. BFS 알고리즘과 달리 A* 알고리즘은 다소 생소할 수 있으나, 실무에서는 A* 알고리즘을 훨씬 많이 사용한다.(애초에 BFS 알고리즘의 진화 버전). 따라서 이번 데이터 분석 프로젝트를 통해서 얼만큼의 성능차이를 보이는지 비교해보고자 한다.
기본이론1 - BFS 알고리즘
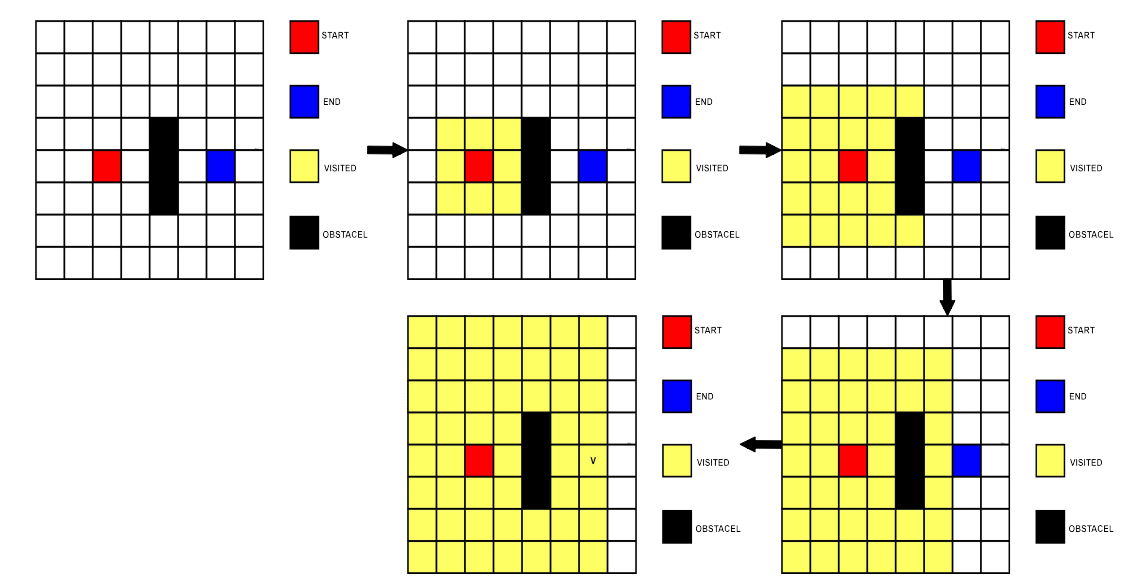
BFS 알고리즘은 전수조사 기법을 사용한다. 먼저 시작 지점과 인접한 지점들을 모두 방문하고, 또 인접한 노드들로부터 인접한 노드들을 모두 방문하고 이런 과정을 모두 거쳐 목적지까지의 최단 거리와 경로를 알아낸다.
기본이론2 - A* 알고리즘
하지만 A* 알고리즘은 여기에 시간적인 측면에서 조금 더 개선된 방식이다. BFS 알고리즘이 해당 지점과 인접한 지점들을 모두 방문하는 반면, A*알고리즘은 인접한 지점들 중 가장 빨리 목적지 까지 도달할 가능성이 높은 지점만 방문하는 것이다. 예를 들어 현재 위치가 a라고 할 때 a와 인접한 지점이 (b,c,d,e)가 있다고 가정해보자. bfs의 경우 (b,c,d,e)로 모두 이동해 해당 지점과 인접한 지점들을 또 탐색한다. 하지만 A*알고리즘의 경우는 (b,c,d,e)중 가장 목적지까지 빨리 도달할 것 같은 지점을 먼저 이동한다. 이때 각 지점 (b,c,d,e)에는 수치 정보가 주어지고, 이 수치를 바탕으로 이동할 장소를 결정한다. 이 수치정보는 평가함수 F이고 F = G + H를 의미한다. G는 시작지점으로 부터 해당 지점까지 실제로 이동하게 될 거리이고, H는 휴리스틱 함수이며 해당 지점으로 부터 목적지까지 얼마만큼 이동해야 할지 예측한 거리이다. A* 알고리즘은, 이 H를 해당지점으로부터 목적지까지 장애물을 고려하지 않은 직선거리로 계산한다. 최종적으로 탐색한 지역 중 F값이 가장 작은 지점부터 먼저 방문을 진행한다. 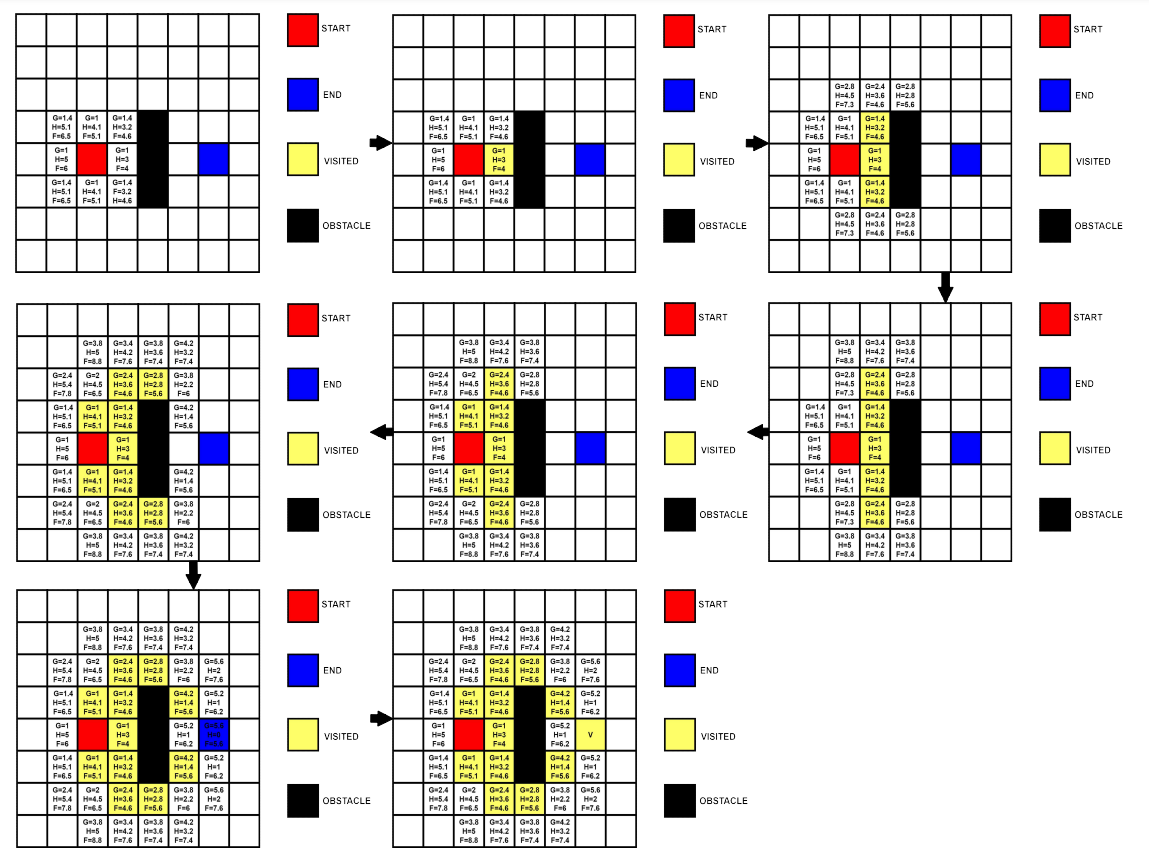
위 그림은 똑같은 상황에서 A* 알고리즘으로 목적지까지의 경로를 찾는 과정을 표현한 것이다. 앞선 BFS 알고리즘에 비해 방문하는 지점이 눈에 띄게 줄어든 것을 알 수 있다. 하지만 사실 A* 알고리즘은 최단경로 문제를 100% 해결하는 알고리즘이 아니다. 이 말은 즉 경로를 찾았음에도 불구하고, 그것이 최단경로가 아닌 경우가 생길수도 있다는 의미이다. 최단 경로를 찾기 위해선 항상 BFS와 같이 전수조사 기법을 사용해야 한다. 하지만 A* 알고리즘은 H라는 예측값을 사용해 경로를 구한다. 이렇게 정답률이 100%인 알고리즘이 아님에도 불구하고 왜 실무에서 A* 알고리즘을 주로 사용할까. 그 이유는 성능대비 비약적으로 높은 정답률을 보이기 때문이다. 따라서 본 프로젝트에서는 실제로 A* 알고리즘과 BFS 알고리즘을 구현해보고, 정답률과 수행시간을 분석해 A* 알고리즘을 사용하면 얼마만큼의 성능 이득을 볼 수 있는지 분석해 보고자한다.
추가로 A* 알고리즘의 성능을 개선해 보고자한다. F = G + H에서 이 휴리스틱 함수 H에 가중치를 곱해 Weighted A* 알고리즘을 구현할 수 있다. 즉 F = G + H가 아닌 F = G + W*H를 사용해서 목적지로의 지향성을 더욱 높일 수 있다. 이 W를 조금씩 여러 번 증가시킬 때 알고리즘의 성능이 어떻게 변하는지도 분석해 보고 최적 가중치를 얻어내 A* 알고리즘의 성능을 개선해보고자 한다
성능 분석 과정 설계
본 프로젝트에서 얻어낼 분석 결과는 두 가지이다.
case 1. N*N map에서 N에 따른 A* 알고리즘과 BFS 알고리즘의 수행시간 분석
case 2. 100*100 map에서 휴리스틱 함수의 Weight에 따른 A* 알고리즘의 수행시간 분석
각 case에서 분석과정은 다음과 같다.
1번 case:
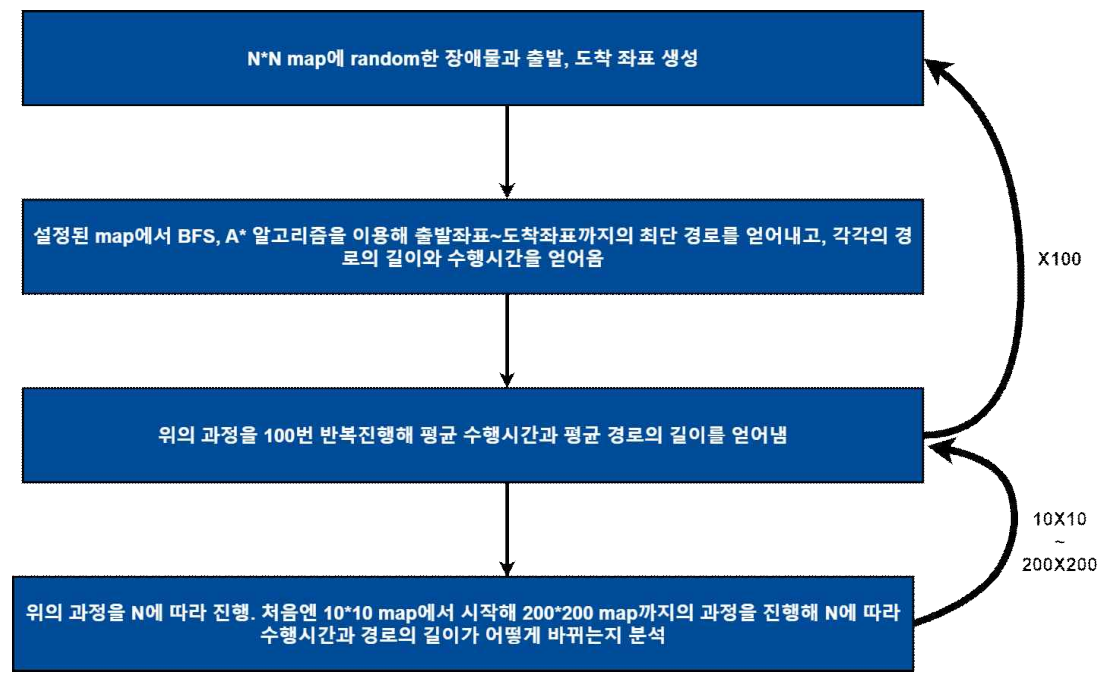
2번 case:
알고리즘 구현
1. 필요한 라이브러리 import
import numpy as np
import queue
import time2. bfs,astar 함수 구현하기
분석을 위해서 직접 BFS 알고리즘과 A* 알고리즘을 구현해보았다. 두 알고리즘을 구현한 함수를 저장한 class를 만든다.
class의 init함수는 다음과 같다.
class PathPlanning:
def __init__(self,n,obstacle_rate):
self.n = n # Map size
self.Map = np.zeros((n,n)) #Map info
self.ob_num = int(n*n*obstacle_rate)
#obstacle number
self.total_array = np.random.choice(n*n,2+self.ob_num,False)
self.total_array_i = (self.total_array/n).astype(int)
self.total_array_j = self.total_array%n
self.coord = np.column_stack((self.total_array_i,self.total_array_j))
#get random start,end,obstacle coordinate
self.Map[self.coord[:2,0],self.coord[:2,1]] = 1
self.Map[self.coord[2:,0],self.coord[2:,1]] = -1
#Update Map info
self.start = self.coord[0]
self.end = self.coord[1] # start,end coordinate
self.dir = np.array([[-1,0],[0,-1],[1,0],[0,1],[1,1],[-1,1],[-1,-1],[1,-1]])
# direction up,down,left,right,,,
self.path_bfs = np.array([[self.end[0],self.end[1]]])
self.path_astar = np.array([[self.end[0], self.end[1]]])
self.W = 1
#Heuristic Weightclass를 생성하면 random한 장애물,시작,도착좌표가 생성될 것이다.
def bfs(self): #bfs algorithm
visit = -np.ones(self.n*self.n) #if not visit : -1
visit[self.start[0]*self.n+self.start[1]] = -2 #start point : -2
q = queue.Queue()
q.put(self.start)
while not q.empty(): #searching end point
cur = q.get()
if (cur == self.end).all() : break
for i in range(8): #searh next position(up,down,left,right direction)
next = cur + self.dir[i]
if (next<0).any() or (next>=self.n).any(): #next position is out of Map
continue
if visit[next[0]*self.n+next[1]] != -1 or self.Map[next[0],next[1]] == -1:
continue
q.put(next)
visit[next[0]*self.n+next[1]] = cur[0]*self.n+cur[1]
Parent = visit[self.end[0]*self.n+self.end[1]] #backtrack Parent position -> path
if Parent == -1 : return []
while Parent != -2: # get path
next = [int(Parent/self.n),int(Parent%self.n)]
self.path_bfs = np.append(self.path_bfs,np.array([next]),axis=0)
Parent = visit[next[0]*self.n+next[1]]
return self.path_bfs[::-1]bfs 알고리즘도 구현해 준다. 최종적으로는 시작~도착 좌표까지의 최단 경로를 return해준다.
def Astar(self):
is_closed = np.zeros((self.n*self.n),dtype=bool)
#closed list info
Parent = -np.ones((self.n*self.n,3))
#Parent node,G,H value info
opened_list = queue.PriorityQueue()
opened_list.put([0,0,0,self.start[0]*self.n+self.start[1]])
#opend list info : [F,G,H,index]
Parent[self.start[0]*self.n+self.start[1]] = np.array([-1,0,0])
#set start node info
while not opened_list.empty():
cur = opened_list.get()
cur_i,cur_j = int(cur[3]/self.n), int(cur[3]%self.n)
if ([cur_i,cur_j] == self.end).all() : break # find end node
if cur[0] > Parent[cur[3]][1] + Parent[cur[3]][2] :
continue
is_closed[cur[3]] = True
for i in range(8):
next = [cur_i,cur_j] + self.dir[i]
if (next < 0).any() or (next >= self.n).any():
continue #next position is out of Map
if self.Map[next[0],next[1]] == -1 or is_closed[next[0]*self.n+next[1]]:
continue #next position is visited position
next_G = Parent[next[0]*self.n+next[1]][1]
next_Parent = Parent[next[0]*self.n+next[1]][0]
cur_G = cur[1] +((self.dir[i][0]-0)**2+(self.dir[i][1]-0)**2)**0.5
if next_Parent == -1 or next_G > cur_G: #Update G,Parent
Parent[next[0]*self.n+next[1]][0] = cur[3] #parent idx set
G = Parent[next[0]*self.n+next[1]][1] = cur_G #G
H = Parent[next[0]*self.n+next[1]][2] = self.Heuristic(next[0],next[1]) #H
F = G+H
opened_list.put([F,G,H,next[0]*self.n+next[1]])
P = Parent[self.end[0]*self.n+self.end[1]][0] #Backtrack Parent position -> path
if P == -1 : return []
while P != -1:
next = [int(P/self.n),int(P%self.n)]
self.path_astar = np.append(self.path_astar,np.array([next]),axis=0)
P = Parent[next[0]*self.n+next[1]][0]
return self.path_astar[::-1]A* 알고리즘도 구현해 준다.
def Heuristic(self,i,j):
end_i = self.end[0]
end_j = self.end[1]
return self.W*((end_i-i)**2+(end_j-j)**2)**0.5A* 알고리즘에서 사용하는 휴리스틱 함수도 넣어준다.
이렇게 PathPlanning을 만든후, 다음과같이 class를 생성하고 Map과 bfs,astar 함수를 호출하면 다음과 같은 결과를 얻는다.
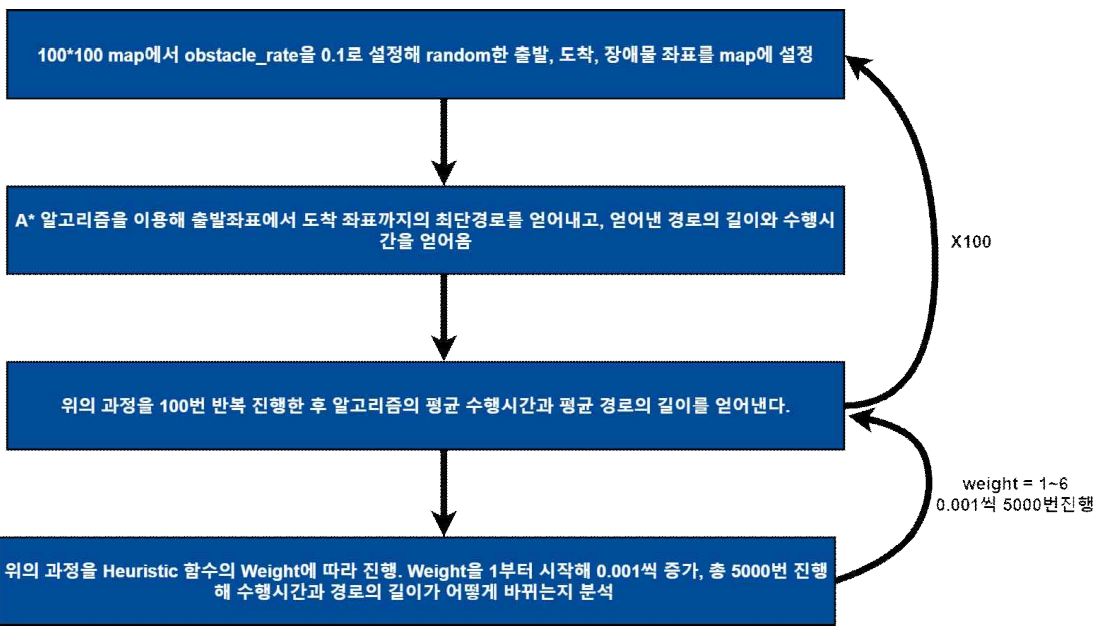
data_analysis = PathPlanning(n=10,obstacle_rate=0.1)
print(data_analysis.Map)
print("BFS path: ", data_analysis.bfs())
print("A* path: ", data_analysis.Astar())output:
데이터 분석 코드 구현
필요한 라이브러리 import
from PathPlanninglib import PathPlanning
import numpy as np
import time
import pandas as pd
import matplotlib.pyplot as plt성능 분석을 위한 class 구현
class Benchmarks:
def __init__(self):
self.bfs_astar_analysis = pd.DataFrame(columns=['bfs time','astar time','weighted astar time'])
self.bfs_astar_analysis2 = pd.DataFrame(columns=['bfs path' , 'astar path','weighted astar path'])
self.index = np.arange(1,6,0.01)
self.astar_weight_analysis = pd.DataFrame(index=self.index)
self.astar_weight_analysis2 = pd.DataFrame(index=self.index)
self.epochs = 100
def get_score_astar_bfs(self,model=PathPlanning):
start = time.time()
bfs_path =model.bfs()
end = time.time()
bfs_performance = (end - start)
start = time.time()
astar_path = model.Astar()
end = time.time()
astar_performance = (end - start)
model.path_astar = np.array([[model.end[0], model.end[1]]])
model.W = 1.1
start = time.time()
weighted_astar_path = model.Astar()
end = time.time()
weighted_astar_performance = (end-start)
return [bfs_performance,astar_performance,weighted_astar_performance],[len(bfs_path),len(astar_path),len(weighted_astar_path)]
def astar_bfs_average(self,n,o_r):
total_time = np.empty((0,3))
total_path = np.empty((0,3))
for i in range(self.epochs):
model = PathPlanning(n=n,obstacle_rate=o_r)
t,p = self.get_score_astar_bfs(model)
total_time=np.append(total_time,np.array([t]),axis=0)
total_path=np.append(total_path,np.array([p]),axis=0)
return total_time.sum(0)/self.epochs,total_path.sum(0)/self.epochs
def astar_bfs_benchmark(self,n):
for i in range(10,n):
result_time,result_path = self.astar_bfs_average(i,o_r=0.2)
new_row1 = {'bfs time': result_time[0], 'astar time': result_time[1], 'weighted astar time':result_time[2]}
new_row2 = {'bfs path': result_path[0], 'astar path': result_path[1], 'weighted astar path': result_path[2]}
print(i,": ",new_row1,new_row2)
self.bfs_astar_analysis.loc[i] = new_row1
self.bfs_astar_analysis2.loc[i] = new_row2
def get_score_astar_weight(self,model=PathPlanning):
start = time.time()
path = model.Astar()
end = time.time()
return (end-start),len(path)
def astar_weight_average(self,n,o_r,w):
total_time=np.empty((0,1))
total_path=np.empty((0,1))
for i in range(self.epochs):
model=PathPlanning(n=n,obstacle_rate=o_r)
model.W = w
t,p = self.get_score_astar_weight(model)
total_time=np.append(total_time,np.array([[t]]),axis=0)
total_path=np.append(total_path,np.array([[p]]),axis=0)
return total_time.sum(0)/self.epochs,total_path.sum(0)/self.epochs
def astar_weight_benchmark(self,N,n,w):
for i in range (10,N):
col_time = np.array([])
col_path = np.array([])
for j in range(n):
result_time,result_path = self.astar_weight_average(i,0.1,1+w*j)
col_time = np.append(col_time,result_time[0])
print(1+w*j,":", result_time[0] , result_path[0])
col_path = np.append(col_path,result_path[0])
self.astar_weight_analysis[i] = col_time
self.astar_weight_analysis2[i] = col_path
def matplot_all(self):
self.bfs_astar_analysis.to_csv("time.csv",mode='w')
self.bfs_astar_analysis2.to_csv('path.csv',mode='w')
self.bfs_astar_analysis.plot()
plt.show()
self.bfs_astar_analysis2.plot()
plt.show()
def run_benchamrk(self):
self.astar_bfs_benchmark(200)
self.matplot_all()
앞서 보여주었던 순서도 대로 성능을 분석하는 class를 만든다.
if __name__ == "__main__":
a = Benchmarks()
a.run_benchamrk()main함수에서 class를 생성하고 run_benchmark()함수를 호출하면, 바로 앞서 보여주었던 두가지 case에 대한 성능분석 절차를 진행하고 그래프를 출력해준다. 또한 csv 파일도 생성된다.
결과
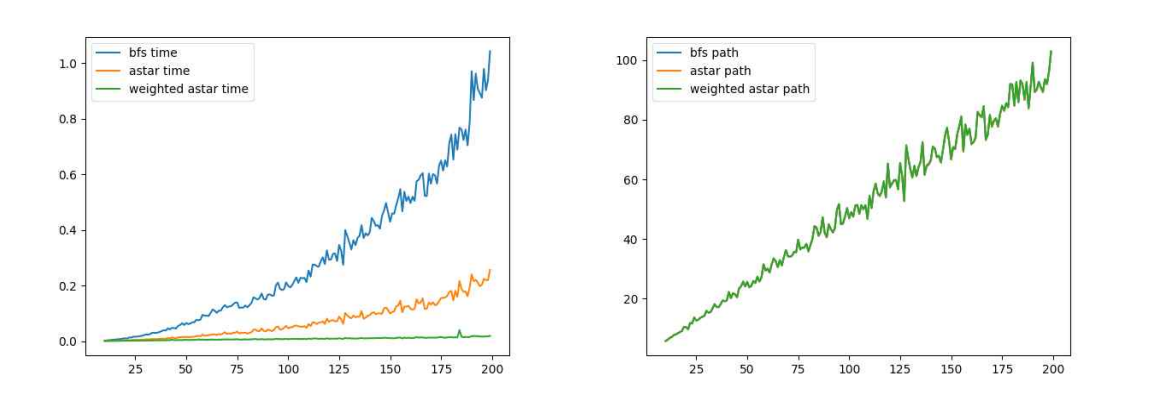
1. case1 N에 따른 A* 알고리즘과 BFS 알고리즘의 수행시간 변화
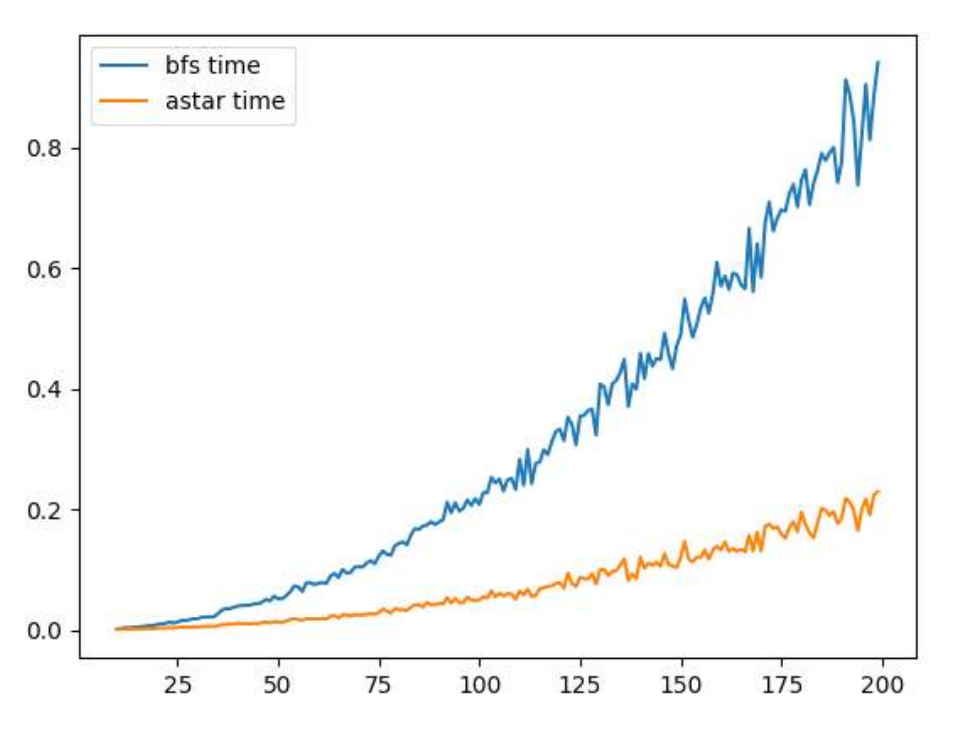
가로축이 input size N이고 세로축이 평균 수행시간이다. BFS 알고리즘은 예측되는 결과와 같이 input size에 대해 거의 N² 만큼의 증가율을 보이는 것을 알 수 있다. 반면 A* 알고리즘의 경우에는 정확한 증가율은 알 수 없었지만 A*보다는 증가율이 더 낮은 것으로 보였고, 실제 수행시간도 항상 더 작다는 것을 알 수 있다. 증가율이 낮기 때문에, input size가 200보다 더 커질 때에도 성능차이는 더욱더 많이 날 것으로 보인다.
2. case1 A* 알고리즘과 BFS 알고리즘을 통해 얻은 경로의 길이
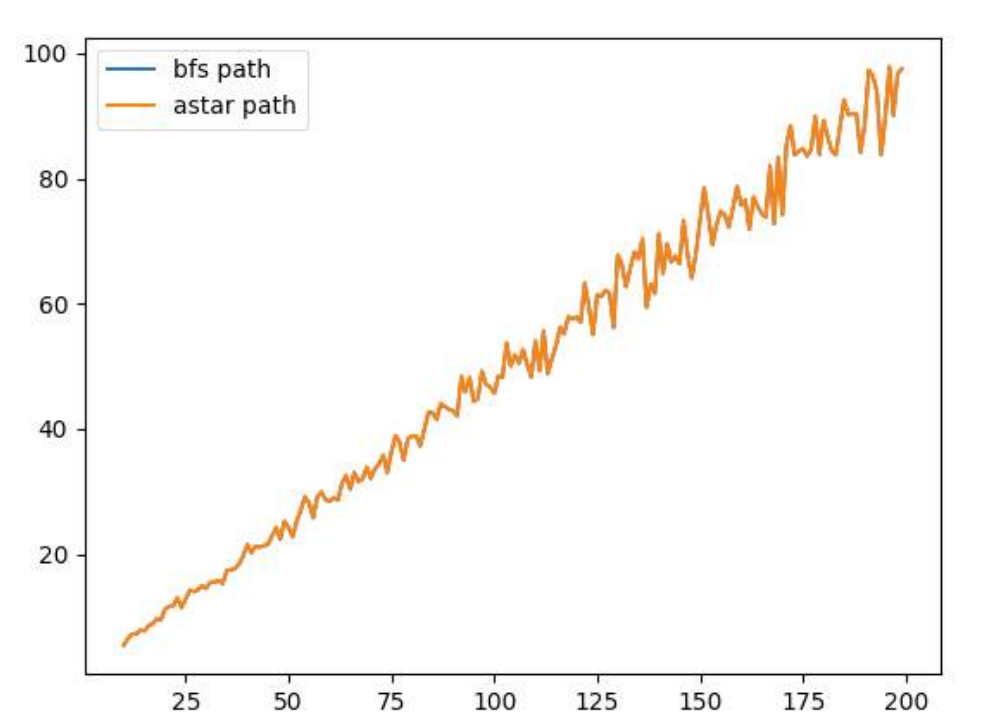
언뜻 보면 하나의 그래프 같지만 실제로는 두개의 그래프가 겹쳐서 나머지 하나의 그래프가 거의 보이지 않는 것이다. 이처럼, input size가 증가함에도 불구하고, A* 알고리즘과 BFS 알고리즘이 return한 경로의 길이는 거의 똑같다는 것을 알 수 있다. 즉 input size와 상관없이 A* 알고리즘은 매우 높은 정답률을 보여준다.
3 case2 W에 따른 A* 알고리즘의 수행시간, CSV파일에 저장된 데이터
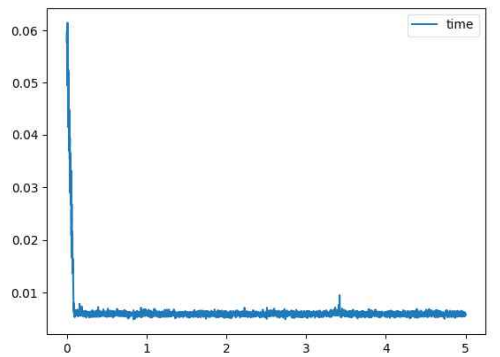
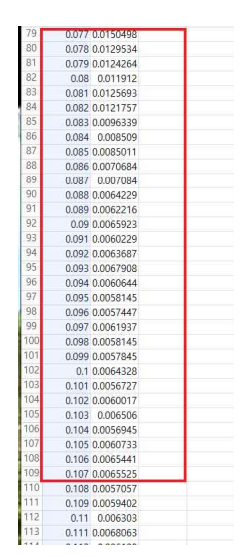
그래프의 가로축은 W=1에 더한 값을 의미한다. 즉 가중치가 1.000~6.000일 때 A* 알고리즘의 수행시간이 어떻게 변하는지 보여주는 그래프이다. 그래프 상에선 특정 임계값에 도달할 때까지 수행시간이 대폭 감소하는 것을 알 수 있고 해당 값에 도달하면 거의 변화하지 않고 일정하게 유지된다. 실제 데이터들을 csv파일에 저장해 확인해 본 결과 이 임계값이 0.1정도라는 것을 확인했다. 즉 가중치가 1.1이상이면 높은 성능의 A*알고리즘을 구현할 수 있다.
4 case2 W에 따른 경로의 길이
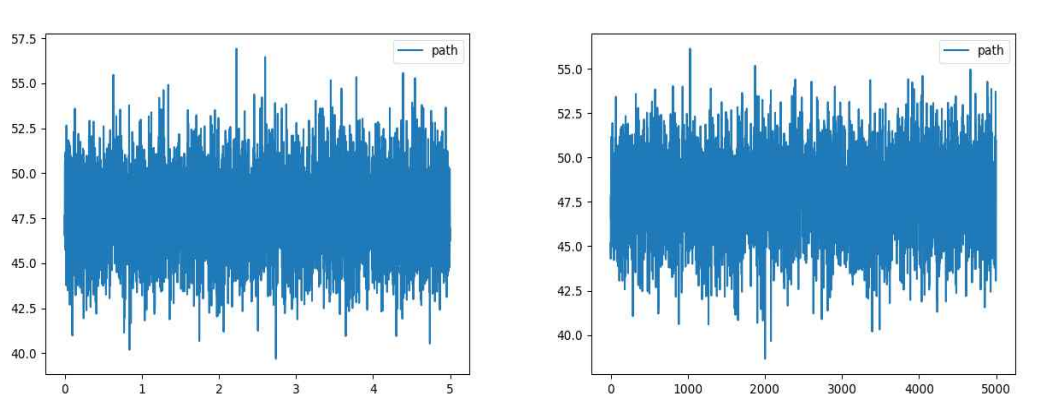
경로의 길이는 딱히 증가하는 추세를 보이지 않는 것으로 보아 가중치가 1~6인 구간 내에서는 정답률에 큰 영향을 끼치지 않는 것으로 보인다. 혹시 가중치의 구간이 너무 작은 것이 아닌가 싶어 가중치를 1~5000으로 설정하고 똑같이 그래프를 그려보니 그래프는 오른쪽 그림과 같이 큰 변화가 없는 것으로 보였다.
결론
N에 따른 수행시간의 증가율을 통해서 A* 알고리즘은 BFS 알고리즘에 비해 훨씬 더 좋은 성능을 보인다는 것을 확인하였다. 여기에 그치지 않고, A* 알고리즘은 N에 따라서 정답률이 점점 떨어질 것이라는 예상과는 달리 N의 크기가 커짐에도 불구하고 거의 100%에 육박하는 정답률을 보였다. big data의 시대로 점점 발전하는 현대 사회에서 input size N의 크기는 앞으로 무한정으로 커질 것으로 보인다. A* 알고리즘은 BFS 알고리즘과 비교해 봤을 때 N이 증가함에 따라 성능 차이가 기하급수적으로 늘어날 것으로 보이기 때문에 이 알고리즘의 가치 역시도 점점 급증할 것으로 보인다. 또한 여기에 그치지 않고 100*100 map에서 A* 알고리즘을 개선해 최적 성능을 보이는 Weight을 데이터 분석 기법을 통해 확인 했다. 그 결과 가중치가 1.1 정도의 값에 도달했을 때 까지 수행시간이 10배 넘게 감소한다는 것을 알 수 있었고, 이후부터는 항상 같은 수행시간을 유지한다. 혹시나 가중치가 증가했을 때 정답률이 떨어지는 것이 아닌지 경로의 길이를 출력해 봤더니, 경로의 길이는 딱히 증가하는 추세를 보이지 않았다. 따라서 Weight과 정답률과는 상관관계가 없다는 결론을 얻을 수 있었고 A* 알고리즘을 개선하기 위해서는 Heuristic 함수에 적어도 1.1 이상의 가중치를 곱하는 것이 좋다는 결론을 얻게 되었다.
가중치를 1.1로 두고 input size N에 따른 수행시간을 BFS, 일반 A* 알고리즘과 비교해봤을때의 결과는 다음과 같다.