오차역전파법
매개변수 가중치의 기울기를 좀더 효율적으로 계산하기 위한 방법.
base 개념 -1 : 계산그래프
어떤 문제를 그래프로 표현해 해결하는 방법
문제 : 만약 1개가 100원인 사과를 2개사는데 소비세가 10% 부과된다고 해보자. 이 경우 내가 지불해야 하는 금액은 얼마인가?
위 문제를 계산그래프로 나타내면 다음과 같다.
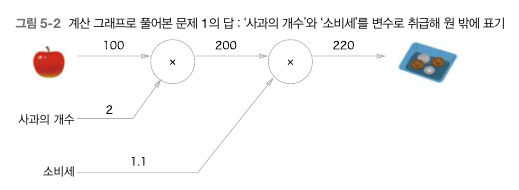
게산그래프의 규칙: 항상 edge는 숫자로, node는 함수(연산기호)로 나타낸다.
base 개념 -2: 순전파
이렇게 만든 그래프를 왼쪽에서 오른쪽으로 진행시켜 계산을 하는것
이 계산 그래프는 국소적 특징을 가짐. 국소적 특징이란 각각의 노드가 자신과 관련된 계산 이외에는 아무것도 신경쓸 필요가 없다는 것을 의미. 이 이점 때문에 계산 그래프를 이용하며, 미분을 효율적으로 계산할 수 있게해주는 특징이다.
위의 문제에서 사과가격이 증가했을 때 전체 지불금액이 얼만큼 오르는지, 즉 사과 가격에 대한 전체 금액의 미분값은 어떻게 구할까. 이는 역전파로 구할 수 있다.
(사과가격: x, 지불 금액 : L) = dL/dx = 미분값. 사과값이 아주 조금 올랐을 때 지불 금액이 얼마만큼 증가하느냐를 표시한 것
실제로 어떻게 구하는지 자세하게는 나중에 보고 일단 그림을 통해 확인
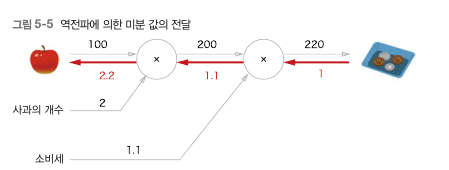
위의 과정을 통해 사과가격의 미분값은 2.2라는 것을 알 수 있음. 즉 사과가 1원오르면 최종금액은 2.2원 오른다는 것을 의미한다.
base 개념 -3: 연쇄법칙
합성함수란 여러 함수로 구성된 함수. 연쇄법칙은 합성함수의 미분에 대한 성질이며. 다음과 같이 정의됨
합성함수의 미분은 합성함수를 구헝하는 각 함수의 미분의 곱으로 나타낼 수 있다.예를들어 z = t^2 과 t = x + y 라는 식이 있다고 했을때. dz/dx 는 dz/dt와 dt/dx의 곱으로 나타낼 수 있음.
실제로 구해보면 dz/dx = dz/dt * dt/dx 이때 dz/dt = 2t, dt/dx = 1 따라서 dz/dx = 1 * 2t = 2t = 2(x+y)가 된다.
연쇄법칙을 계산 그래프로 나타내면 다음과 같다.
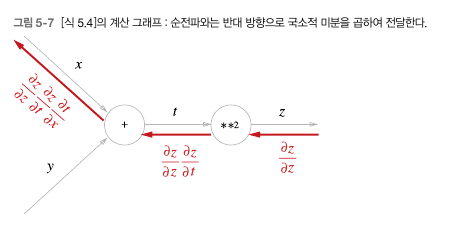
이를 적용해 사과쇼핑에서 세가지 변수에 대한 지불금액의 미분값을 구할 수 있다.
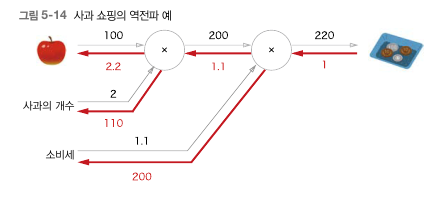
사과 가격에대한 지불금액의 미분값 : 2.2 (사과 1원이 오르면 지불금액은 2.2원이 오른다.)
사과 갯수에 대한 지불금액의 미분값: 110 (사과 1개가 증가하면 지불금액은 110원이 오른다.)
소비세에 대한 지불금액의 미분값 : 200 (소비세 100%가 증가하면 지불금액은 200원이 오른다.)
어떻게 위의 값이 구해질까? 맨 오른쪽부터 시작해 역전파를 진행한다.
처음은 항상 1로 설정. 그다음 200과 1.1에 대한 미분값들을 1과 곱한다. 곱하기 연산의 경우 t = xy라고 했을때 x에대한 미분값은 y, y에 대한 미분값은 x가 된다. 따라서 곱하기에서 미분값은 항상 서로 상대하는 값을 가지게됨.
따라서 200 * 1.1 = 220부분에서 200에서의 미분값은 1.1 * 1이되고, 1.1에서의 미분값은 200 * 1이 된다.
마찬가지로 100 * 2 = 200을 보자. 100에서는 미분값은 2가되고, 2에서 미분값은 100이된다. 연쇄법칙에 따라서 이전의 미분값을 현재미분값을 곱해주면 각각 2.2, 110이된다. 따라서 위의 결과가 나오게 되는 것이다.
앞의 개념들을 토대로 다른 함수들의 계산그래프와 역전파를 구할 수 있다.
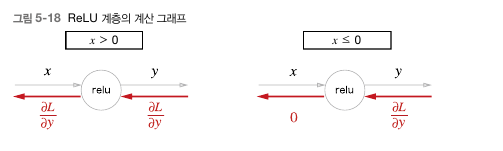
ReLU 계층의 계산그래프와 역전파.
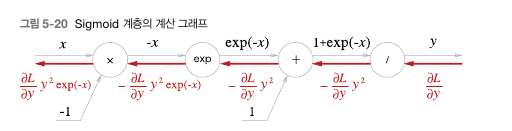
Sigmoid 계층의 계산그래프와 역전파
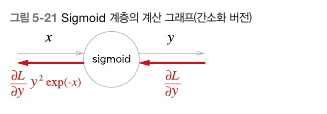
위를 X-SIGMOID-Y로 통합하면 다음과 같다.
이때 y^2 * exp(-x)는 y(1-y)와 같아지므로 다음과같이 간소화 시킬 수 있다.
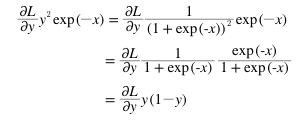
최종적으로 Sigmoid 계층의 역전파는 다음과 같다.

