딥러닝 -4 (실제로 구현해보기)

앞선 과정에서는 단일 변수의 계산그래프를 표현한 것. 이를 행렬로 확장해서 계산그래프를 그릴 수 있다.

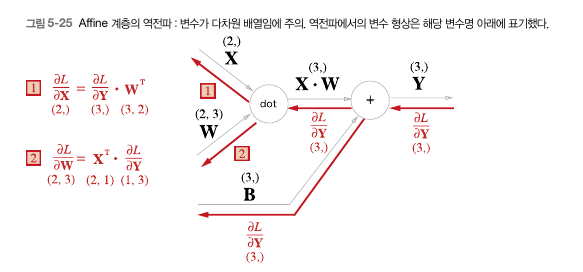
신경망에서 학습은 위의 WX+B와 활성화함수의 반복을 통한 순전파와, 역전파로인한 매개변수 갱신으로 이루어진다. 이때 WX+B의 계산이 이루어지는 계층을 AFFINE 계층이라고 할 때 AFFINE 계층 클래스를 다음과 같이 구현 시킬 수 있다.

- 계층으로 표현한 신경망

class Affine:
    def __init__(self,W,b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None

    def forward(self,x):
        self.x = x
        out = np.dot(x,self.W)+self.b

        return out

    def backward(self,dout):
        dx = np.dot(dout,self.W.T)
        self.dW = np.dot(self.x.T,dout)
        self.db = np.sum(dout,axis= 0)

- Affine class 구현

# coding: utf-8
import numpy as np


def identity_function(x):
    return x


def step_function(x):
    return np.array(x > 0, dtype=np.int)


def sigmoid(x):
    return 1 / (1 + np.exp(-x))    


def sigmoid_grad(x):
    return (1.0 - sigmoid(x)) * sigmoid(x)
    

def relu(x):
    return np.maximum(0, x)


def relu_grad(x):
    grad = np.zeros(x)
    grad[x>=0] = 1
    return grad
    

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x) # 오버플로 대책
    return np.exp(x) / np.sum(np.exp(x))


def mean_squared_error(y, t):
    return 0.5 * np.sum((y-t)**2)


def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)
        
    # 훈련 데이터가 원-핫 벡터라면 정답 레이블의 인덱스로 반환
    if t.size == y.size:
        t = t.argmax(axis=1)
             
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size


def softmax_loss(X, t):
    y = softmax(X)
    return cross_entropy_error(y, t)

- functions.py (모든 활성화 함수, 손실함수를 정리해놓은 파일)

import numpy as np
from functions import *
from util import im2col, col2im


class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0

        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx


class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx


class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        
        self.x = None
        self.original_x_shape = None
        # 가중치와 편향 매개변수의 미분
        self.dW = None
        self.db = None

    def forward(self, x):
        # 텐서 대응
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x

        out = np.dot(self.x, self.W) + self.b

        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        
        dx = dx.reshape(*self.original_x_shape)  # 입력 데이터 모양 변경(텐서 대응)
        return dx


class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None # 손실함수
        self.y = None    # softmax의 출력
        self.t = None    # 정답 레이블(원-핫 인코딩 형태)
        
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # 정답 레이블이 원-핫 인코딩 형태일 때
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size
        
        return dx

- layers.py 모든 계층 class를 정리해놓은 파일

import numpy as np
from layers import *
from collections import OrderedDict

class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 가중치 초기화
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) 
        self.params['b2'] = np.zeros(output_size)

        # 계층 생성
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

        self.lastLayer = SoftmaxWithLoss()
        
    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        
        return x
        
    # x : 입력 데이터, t : 정답 레이블
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)
        
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
        
    # x : 입력 데이터, t : 정답 레이블
    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)
        
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 결과 저장
        grads = {}
        grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

        return grads
        

- Network.py (2층 신경망 class)

import numpy as np
import Network as nt
from mnist import load_mnist

(x_train,t_train) , (x_test,t_test) = load_mnist(normalize=True,one_hot_label=True)
train_loss_list = []


iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size/batch_size,1)

net = nt.TwoLayerNet(784,50,10)

for i in range(iters_num):
   print(i)
   batch_mask = np.random.choice(train_size,batch_size)
   x_batch = x_train[batch_mask]
   t_batch = t_train[batch_mask]

   grad = net.gradient(x_batch,t_batch)

   for key in ('W1','b1','W2','b2'):
       net.params[key] -= learning_rate*grad[key]

   loss = net.loss(x_batch,t_batch)
   train_loss_list.append(loss)

print(train_loss_list)

- mnist data set 불러와 학습시켜보기 마지막에 손실함수 값 list를 출력시키면, 값이 점점 줄어드는것을 확인할 수 있다.