지금까지 살펴본 신경망은 피드포워드(feed forward) 라는 유형의 신경망.
하지만 시계열 데이터를 다루기에는 적절한 형태는 아니다. 그래서 RNN이등장한다.
구조
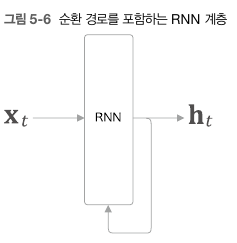
RNN의 구조는 다음과같다. 기본적으로 입력데이터를 받으면서, 이전 시각의 출력값도 같이 고려해 계산한다.
이를 펼치면 다음과 같은 구조가 나온다.
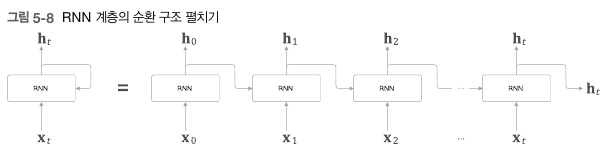
실제로 이 책에서 구현한 방식은 , RNN 계층 하나를 구현하고, 이를 T개를 연결시킨 TimeRNN을 만들어 구현시킨다.
RNN계층에서 출력하는 값의 계산식은 다음과 같다.
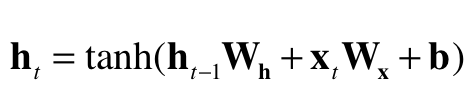
ht는 t시각에서의 출력값이고 W는 가중치, b는 편향이다. RNN 계층 하나에는 기본적으로 가중치를 두개 사용한다.
Truncated BPTT
RNN구조에서도 위의 그림과같이 펼친 상태로 가중치 매개변수 갱신을 위해 오차역전파법을 사용한다. 하지만 시간이 무한정으로 길어지면 어떻게 될까.
역전파는 이전의 미분값인 dout에 현재 계층의 미분값을 곱해가면서 전해진다. 이때 이 미분값이 보통 0.1정도라고 가정하고, 단어 시퀀스의 길이가 1000이라고 생각해보자. 그럼 역전파가 진행되면 진행될수록, 미분값은 거의 0에 수렴할 정도로 매우 작아질 것이다.
이 미분값만큼 가중치 매개변수를 갱신해야 하는데, 너무 작으면, 그만큼 학습 효율이 굉장히 떨어진다.
반대로 미분값이 1이상의 어떤 값이라고 생각해보자. 이럴경우 역전파가 진행될 수록 미분값이 기하급수적으로 커질것이다. 이렇게되면 기울기 폭발이 일어나 overflow가 일어날 가능성이 높아진다. 따라서 RNN에서 역전파의 연결은 적당한 길이로 잘라내 잘라낸 블록단위로 오차역전파법을 수행한다. 이를 Truncated BPTT라고 한다.
RNN 계층 구현하기
앞서 말한 식을 이용해 RNN계층의 forward와 backward를 구현할 수 있다.
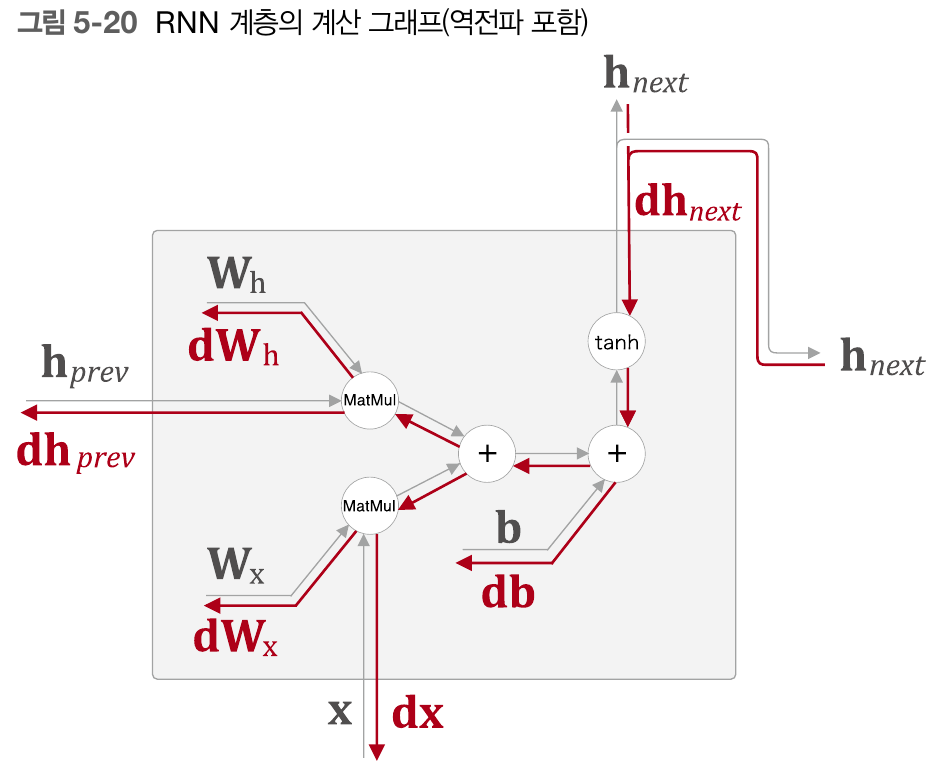
forward는 앞서 말한 식을 통해 구현하며, 역전파는 다음 RNN 구조의 계산그래프를 보며 한단계 한단계 거쳐가다보면 차분히 구할 수 있다.
class RNN:
def __init__(self,Wx,Wh,b):
self.params = [Wx,Wh,b]
self.grads = [np.zeros_like(Wx),np.zeros_like(Wh),np.zeros_like(b)]
self.cache = None
def forward(self,x, h_prev):
Wx, Wh, b = self.params
t = np.matmul(h_prev,Wh) + np.matmul(x,Wx) + b
h_next = np.tanh(t)
self.cache = (x,h_prev,h_next)
return h_next
def backward(self,dh_next):
Wx, Wh, b = self.params
x , h_prev,h_next = self.cache
dt = dh_next * (1 - h_next**2) #tanh 미분 -> 1 - y**2
db = np.sum(dt,axis=0)
dWx = np.matmul(x.T,dt)
dWh = np.matmul(h_prev.T,dt)
dh_prev = np.matmul(dt,Wh.T)
dx = np.matmul(dt,Wx.T)
self.grads[0][...] = dWx
self.grads[1][...] = dWh
self.grads[2][...] = db 먼저 tanh(x)의 미분값을 살펴보자. y = tanh(x)를 미분하면 1 - y^2이라는 것을 알 수 있다.(https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=handuelly&logNo=221824080339)
따라서 dt는 dh_next * (1 - h_next**2)이 된다.
그다음 덧셈 계층이 나오는데, 덧셈계층에서의 역전파는 그대로 진행되므로 db는 그대로 dt를 가져오고, db와 형상을 맞춰야 하기
np.sum(dt)가 된다.
그다음에도 덧셈 계층이 나오므로 그대로 진행하고, MatMul 계층이 나온다. MatMul 계층에서는 앞선 Affine 계층을 생각하면 된다. Y = WX 에서 Y를 X에대해 미분한 값은 W, Y를 W에대해 미분한 값은 X가 되므로 각각 상대되는 값을 dt와 matmul한 값이 된다.
TimeRnn 구현하기
앞선 RNN은 RNN하나, 즉 단어 하나를 입력받는 계층이다. 현재 목표는 N개의 단어 sequence를 입력받는 RNN을 구현하는 것이 목적이기 때문에, T개의 RNN을 연결하는 TimeRNN을 구현한다.
class TimeRNN:
def __init__(self, Wx, Wh,b,stateful = False): #stateful = true -> 순전파를 끊지않고 전파하겠다. ,stateful = false -> 은닉상태를 영행렬로 초기화
self.params = [Wx,Wh,b]
self.grads = [np.zeros_like(Wx),np.zeros_like(Wh),np.zeros_like(b)]
self.layers = None
self.h,self.dh = None,None
self.stateful = stateful
def set_state(self,h):
self.h = h
def reset_state(self):
self.h = None
def forward(self,xs):
Wx, Wh, b = self.params
N, T , D = xs.shape
D, H = Wx.shape
self.layers = []
hs = np.empty((N,T,H), dtype='f')
if not self.stateful or self.h is None:
self.h = np.zeros((N,H),dtype='f')
for t in range(T):
layer = RNN(*self.params)
self.h = layer.forward(xs[:,t,:],self.h)
hs[:,t,:] = self.h
self.layers.append(layer)
return hs
def backward(self,dhs):
Wx, Wh, b = self.params
N,T,H = dhs.shape
D, H = Wx.shape
dxs = np.empty((N,T,D),)
dh = 0
grads = [0,0,0]
for t in reversed(range(T)):
layer = self.layers[t]
dx,dh = layer.backward(dhs[:,t,:]+dh)
dxs[:,t,:] =dx
for i, grad in enumerate(layer.grads): #layer.grads = [dWx, dWh, db]를 grads에 넣기 ([0,0,0])
grads[i] += grad
for i, grad in enumerate(grads): # grads에 있는걸 다시 self.grads에 저장
self.grads[i][...] = grad
self.dh = dh
return dxs