문제
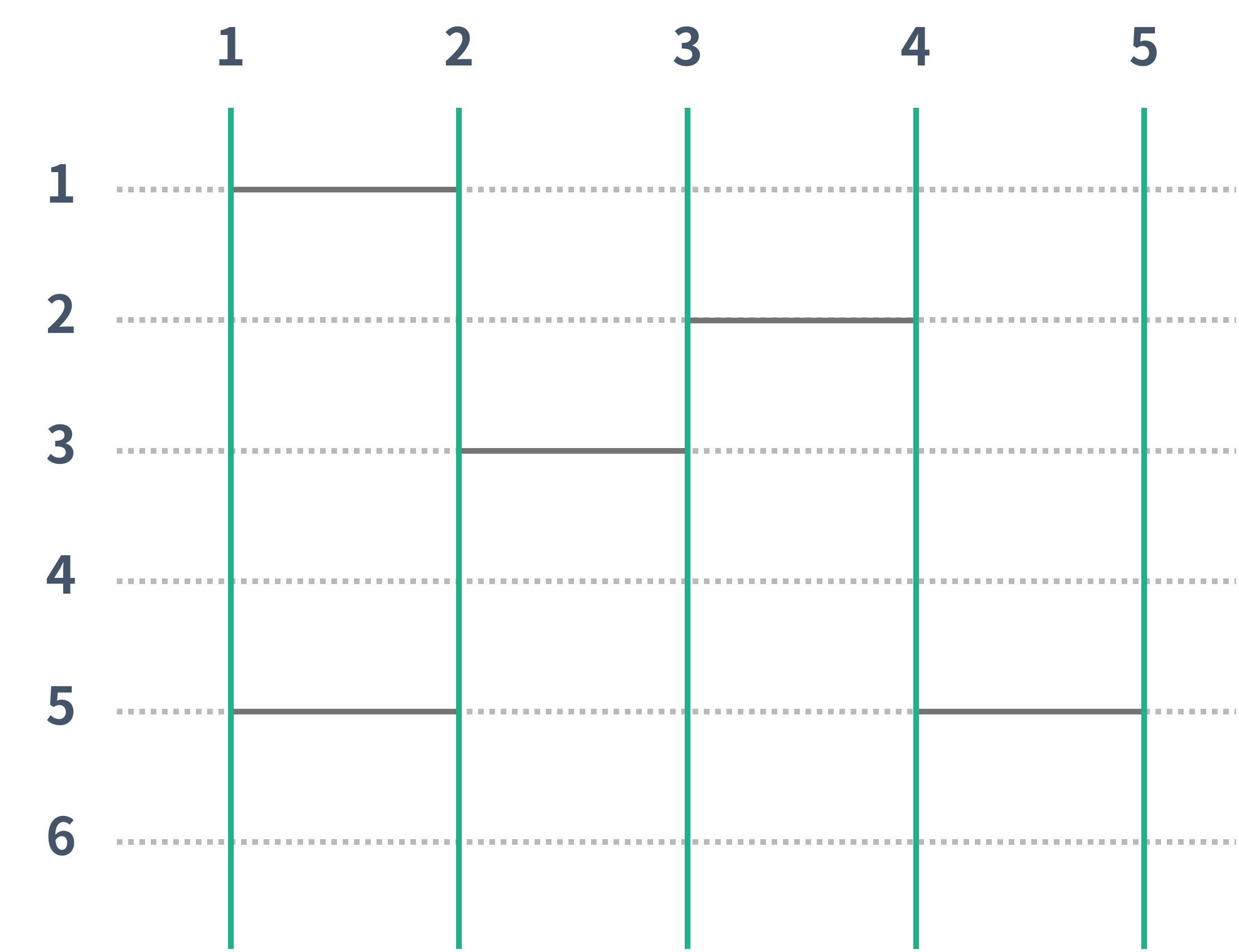
사다리 게임은 N개의 세로선과 M개의 가로선으로 이루어져 있다. 인접한 세로선 사이에는 가로선을 놓을 수 있는데, 각각의 세로선마다 가로선을 놓을 수 있는 위치의 개수는 H이고, 모든 세로선이 같은 위치를 갖는다. 아래 그림은 N = 5, H = 6 인 경우의 그림이고, 가로선은 없다.

초록선은 세로선을 나타내고, 초록선과 점선이 교차하는 점은 가로선을 놓을 수 있는 점이다. 가로선은 인접한 두 세로선을 연결해야 한다. 단, 두 가로선이 연속하거나 서로 접하면 안 된다. 또, 가로선은 점선 위에 있어야 한다.
위의 그림에는 가로선이 총 5개 있다. 가로선은 위의 그림과 같이 인접한 두 세로선을 연결해야 하고, 가로선을 놓을 수 있는 위치를 연결해야 한다.
사다리 게임은 각각의 세로선마다 게임을 진행하고, 세로선의 가장 위에서부터 아래 방향으로 내려가야 한다. 이때, 가로선을 만나면 가로선을 이용해 옆 세로선으로 이동한 다음, 이동한 세로선에서 아래 방향으로 이동해야 한다.
위의 그림에서 1번은 3번으로, 2번은 2번으로, 3번은 5번으로, 4번은 1번으로, 5번은 4번으로 도착하게 된다. 아래 두 그림은 1번과 2번이 어떻게 이동했는지 나타내는 그림이다.
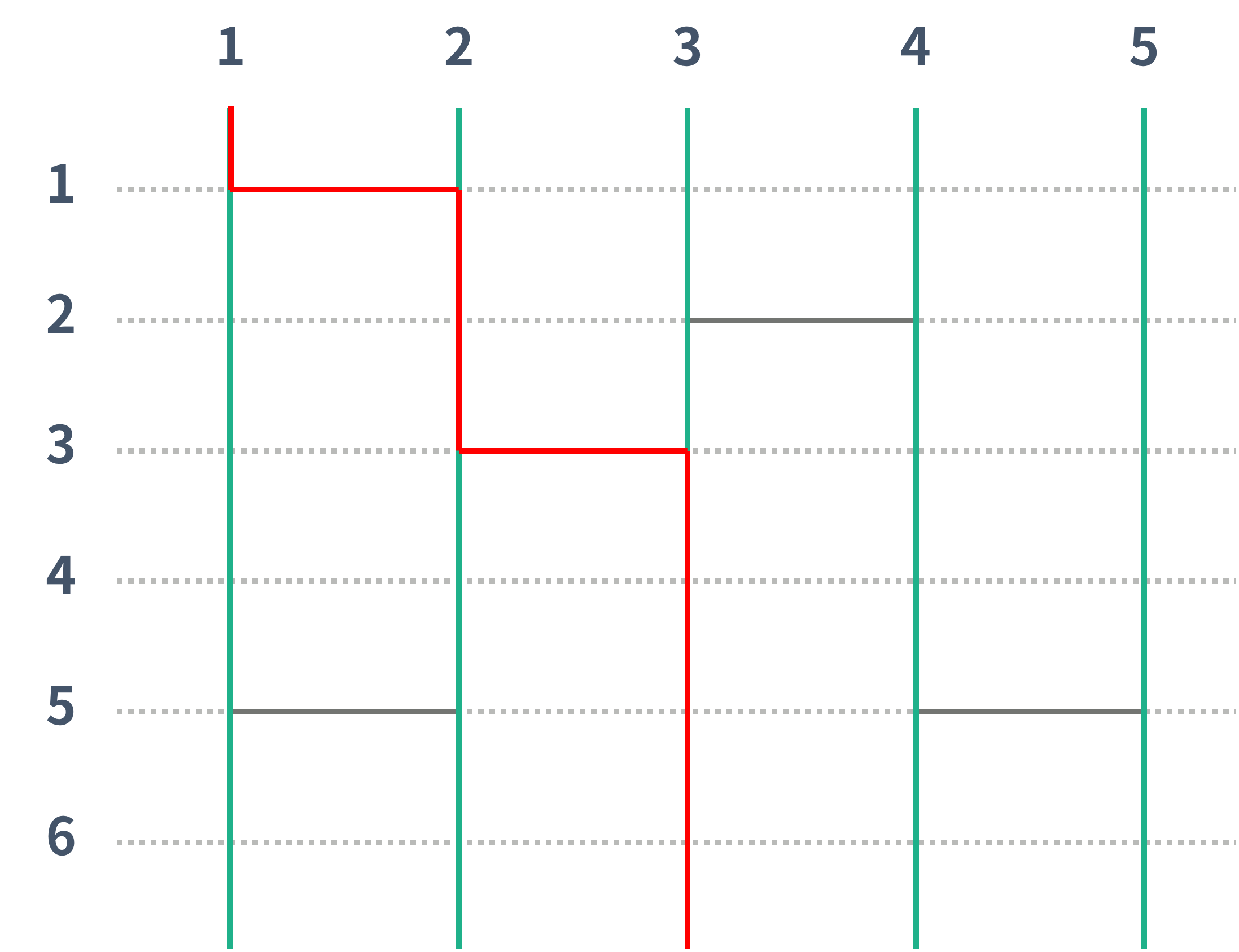
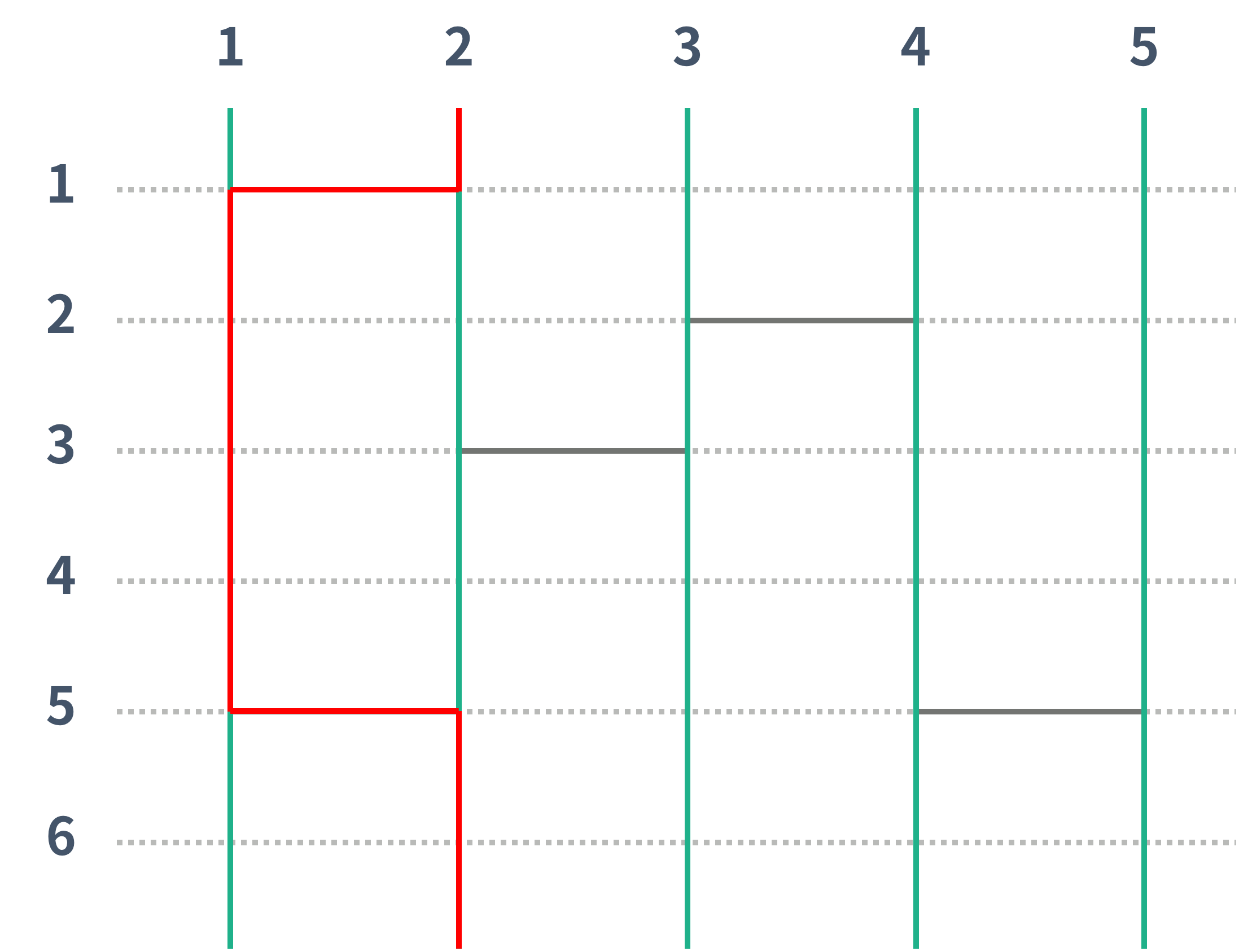
사다리에 가로선을 추가해서, 사다리 게임의 결과를 조작하려고 한다. 이때, i번 세로선의 결과가 i번이 나와야 한다. 그렇게 하기 위해서 추가해야 하는 가로선 개수의 최솟값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 세로선의 개수 N, 가로선의 개수 M, 세로선마다 가로선을 놓을 수 있는 위치의 개수 H가 주어진다. (2 ≤ N ≤ 10, 1 ≤ H ≤ 30, 0 ≤ M ≤ (N-1)×H)
둘째 줄부터 M개의 줄에는 가로선의 정보가 한 줄에 하나씩 주어진다.
가로선의 정보는 두 정수 a과 b로 나타낸다. (1 ≤ a ≤ H, 1 ≤ b ≤ N-1) b번 세로선과 b+1번 세로선을 a번 점선 위치에서 연결했다는 의미이다.
가장 위에 있는 점선의 번호는 1번이고, 아래로 내려갈 때마다 1이 증가한다. 세로선은 가장 왼쪽에 있는 것의 번호가 1번이고, 오른쪽으로 갈 때마다 1이 증가한다.
입력으로 주어지는 가로선이 서로 연속하는 경우는 없다.
출력
i번 세로선의 결과가 i번이 나오도록 사다리 게임을 조작하려면, 추가해야 하는 가로선 개수의 최솟값을 출력한다. 만약, 정답이 3보다 큰 값이면 -1을 출력한다. 또, 불가능한 경우에도 -1을 출력한다.
풀이
사다리를 가로 N 세로 H의 2차원 배열로 구현 할 수 있다. 여기서 배열 안의 숫자에서 0은 비어있는 자리, 1은 N번 세로줄에서 오른쪽으로 연결된 자리, 2는 N번 세로줄에서 왼쪽으로 연결된 자리로 설정한다.
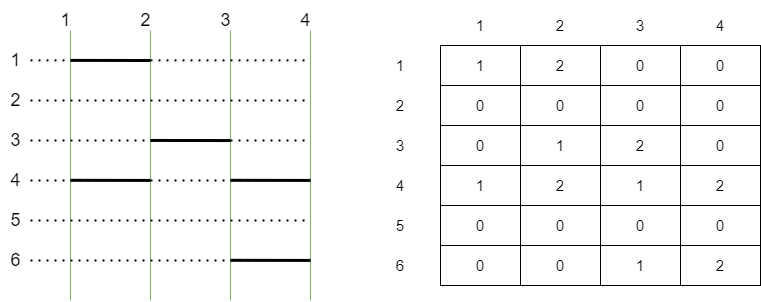
여기서 가로선을 새로 놓을 수 있는 자리를 vector에 저장해 놓는다. 즉,두번 연속으로 0이 되는 곳을 vector에 저장한다. 예를들어 위의 그림에서 vector의 원소는 (1,3)(1,4) , (2,1)(2,2) , (2,2)(2,3) , (2,3)(2,4) , (5,1)(5,2) , (5,2)(5,3) , (5,3)(5,4) , (6,1)(6,2) 가 된다.
결과는 3보다 크면 -1이된다. 즉, 위의 빈곳에서 0개, 1개, 2개, 3개를 선택해 가로선을 놓았을 때 만약 i번 세로선의 결과가 i번이 나오지 않으면 그냥 -1을 띄우고 0,1,2,3을 체크하는 과정에서 결과가 조건을 충족하면 바로 출력하고 EXIT하면 된다.
조합을 이용해 풀면된다. 빈곳중에서 0개를 선택하고 결과가 충족하는지 검사, 빈곳중에 1개를 선택하고 결과가 충족되는지 검사, 빈곳중에 2개를 선택하고 결과가 충족되는지 검사, 빈곳중에 3개를 선택하고 결과가 충족되는지 검사 3보다 크게되면 -1을 출력하고 종료. 이때 주의할 것은 이미 선택된 곳과 겹치는 곳이 있다면 다음 선택에서 선택되면 안된다. 예를들어 위의 빈 곳의 좌표중 두개를 선택 한다고 할 때 (2,1)(2,2)를 이미 선택했다면 두번째 선택에서 (2,2)(2,3)은 이전에 선택된 가로줄과 연속된 가로선이 되기때문에 선택되지 않게 조건을 걸어주어야 한다.
결과가 충족되는지 검사하는 함수는 현재 세로줄 번호를 저장하는 변수 tmp를 만들어 h=0부터 h가 H가 될때까지 tmp를 바꾸어가며 이동시키고 맨 마지막 tmp가 초기 세로줄 번호와 맞으면 통과 아니면 false를 리턴한다. 이 과정을 세로줄 0번부터 N번까지 반복하고 반복문을 다 빠져나오면 true를 리턴한다.
풀었는데 계속 시간초과가 떴다. 조합으로 짰기 때문에 최악의 경우 약 400만번의 연산을 해서 충분 할 것이라 생각했다. 하지만 그뿐만 아니라 400만번 동안 결과가 충족되는지 검사까지 해야되기 때문에 이 검사하는 함수를 잘 짜야되는데,, 사실 세로 H번만의 이동으로 검사가 가능한데 WHILE문으로 가로 세로 모두 이동하도록 짜서 시간 초과가 걸린 것 같다. 코드를 수정하니 바로 정답..
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N, M, H;
int ladder[31][11];
vector<pair<int, int>>empty_space;
void input() { //입력
cin >> N >> M >> H;
for (int i = 0; i < M; ++i) {
int a, b;
cin >> a >> b;
ladder[a - 1][b-1] = 1;
ladder[a - 1][b] = 2;
}
}
bool Tracking() { // 결과를 충족하는가?
for (int i = 0; i < N; ++i) {
int tmp = i;
for (int j = 0; j < H; ++j) {
if (ladder[j][tmp] == 1) {
tmp = tmp + 1;
}
else if (ladder[j][tmp] == 2) {
tmp = tmp - 1;
}
}
if (tmp != i) {
return false;
}
}
return true;
}
void set_garo(int n,int i, int at) { // 비어있는 곳에 가로줄을 n(0,1,2,3)개를 채운 후 결과를 충족하면 n을 출력하고 exit
if (n == i) {
if (Tracking()) {
cout << n;
exit(0);
}
return;
}
for (int k = at; k < empty_space.size(); ++k) {
int x = empty_space[k].first;
int y = empty_space[k].second;
if (ladder[x][y] == 0 && ladder[x][y + 1] == 0) {
ladder[x][y] = 1;
ladder[x][y + 1] = 2;
set_garo(n + 1, i, k + 1);
ladder[x][y] = 0;
ladder[x][y+1] = 0;
}
}
}
void set_empty_space() { //비어있는 곳을 vector에 저장
for (int i = 0; i < H; ++i) {
for (int j = 0; j < N - 1; ++j) {
if (ladder[i][j] == 0 && ladder[i][j + 1] == 0) {
empty_space.push_back(make_pair(i, j));
}
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
input();
set_empty_space();
for (int i = 0; i < 4; ++i) {
set_garo(0, i, 0);
}
cout << -1;
}
