문제
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
- 시작 점
- 시작 방향
- 세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.

2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)
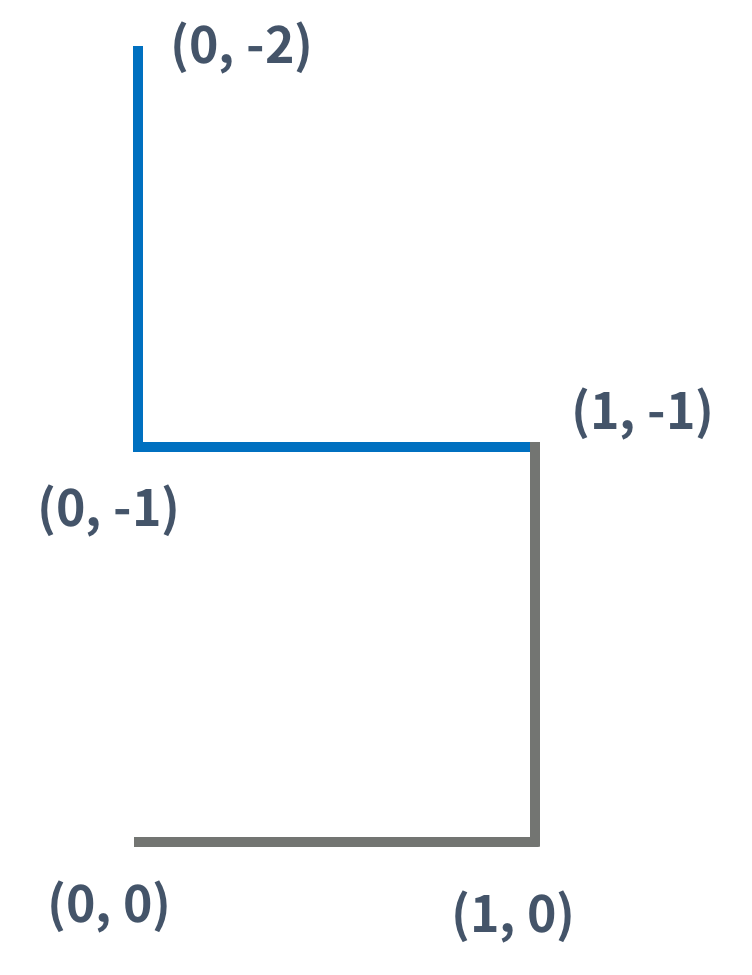
3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.
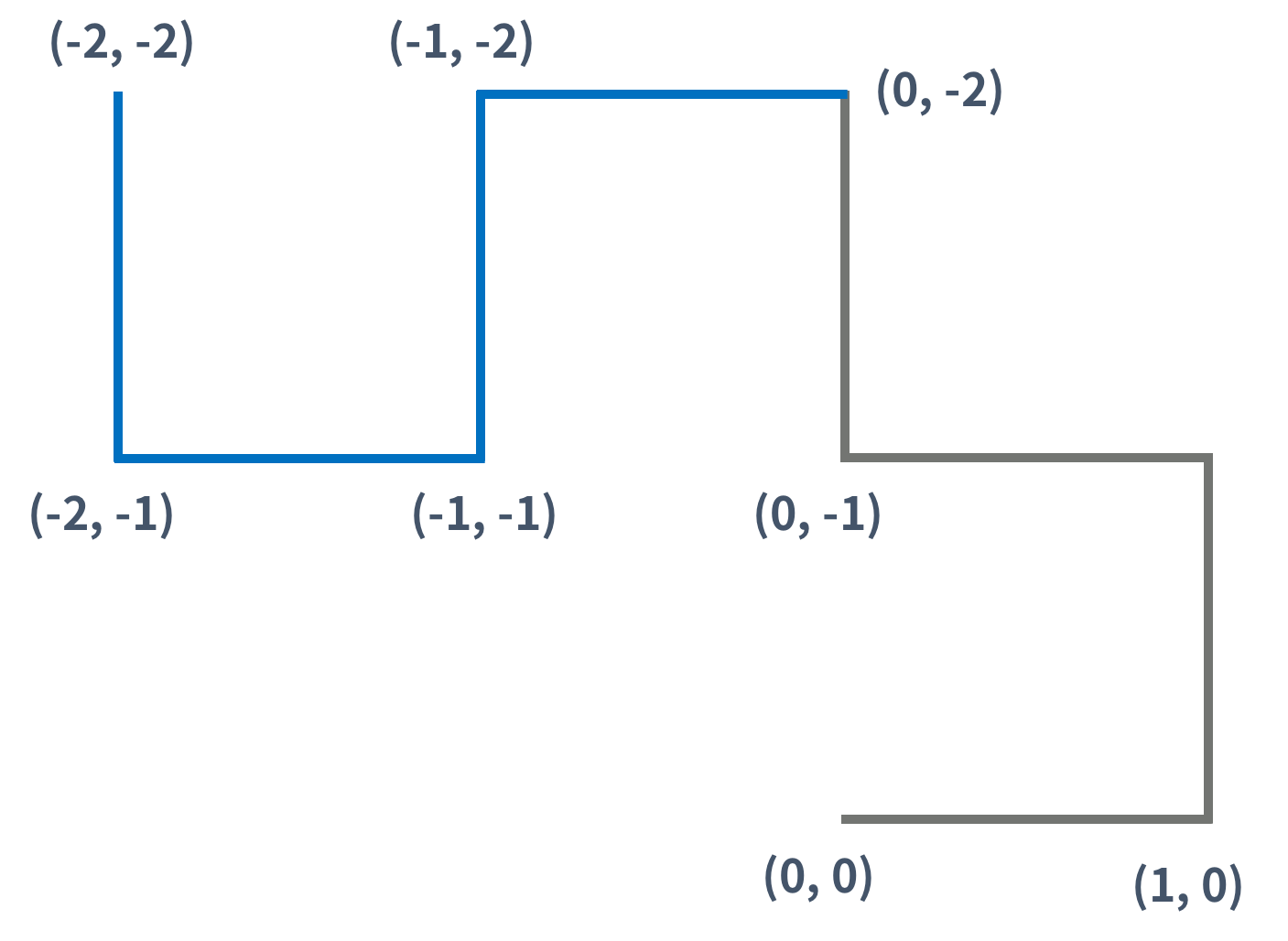
즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
입력
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)
입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다.
방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.
- 0: x좌표가 증가하는 방향 (→)
- 1: y좌표가 감소하는 방향 (↑)
- 2: x좌표가 감소하는 방향 (←)
- 3: y좌표가 증가하는 방향 (↓)
출력
첫째 줄에 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 것의 개수를 출력한다.
풀이
100x100 배열에 드래곤커브에 해당하는 부분을 1로 표시, 아니면 0으로 설정해놓고 arr[i][j] , arr[i+1][j], arr[i][j+1] , arr[i+1][j+1]이 모두 1인 것의 갯수를 count 한다.
드래곤 커브를 표시하는 것은 재귀로 해결한다.
1. 이전세대의 좌표에서 90도 회전시킨 새로운 좌표들을 생성
2. 새로 생성한 새로운 좌표를 이동시켜 끝점과 연결해 연결된 좌표를 현재세대의 좌표로 업데이트한다.
3. 재귀 호출을 통해 현재 세대의 좌표와 끝점좌표를 전달한다.
문제는 어떻게 90도로 회전시키는 좌표를 만들지, 또한 끝점은 어떻게 찾는지이다.
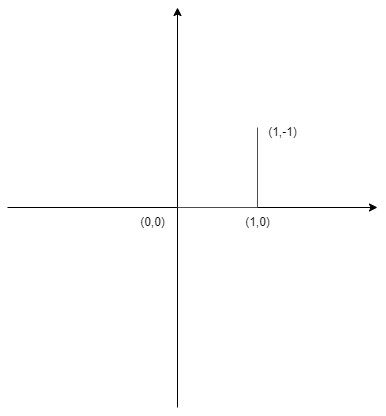
다음과 같은 좌표로 되어있다고 했을때 시계방향으로 90도로 회전하면
아래 그림과 같이된다.

좌표축을 회전킨다고 하면 (0,0) -> (0,0) , (1,0)->(0,1) , (1,-1) -> (1,1) 이 되는것을 알수 있다. 즉 기존 좌표가 (x,y)라 했을 때 모든 좌표를 (-y,x)로 바꾸면 시계방향으로 90도 회전한 좌표가 된다는 것을 알 수 있다.
이때 회전하는것 뿐만이 아니라 이렇게 회전시킨 좌표들을 이전세대 좌표의 끝점에 연결시켜야 한다. 지금 끝점의 좌표가 1,-1이라는 것을 안다고 가정했을 때 회전시킨 좌표중 0,0에서 가장 멀리 떨어진, 즉 이전세대의 끝점을 회전시켜 바꿀 때 나오는 그 좌표가 이전세대의 끝점과 연결되는 것이다.
다음과 같은 예에서는 이전세대의 끝점인 (1,-1)이 (1,1)로 바뀌고 (1,1)과 (1,-1)을 연결 시켜야 하므로 새로운 좌표를 두 점의 차이만큼 새롭게 생긴 좌표들을 모두 이동시킨다. 즉 (1,-1) - (1,1) = (0,-2)만큼 모두 이동시킨다.
그렇게 나온 결과는 (0,0)+(0,-2) , (0,1)+(0,-2) , (1,1)+(0,-2) = (0,-2),(0,-1),(1,-1)이 되는것이다.

이때 이는 끝점의 좌표가 1,-1이라는것을 안다고 가정할 때 가능한 일이다. 따라서 이전세대에서 현재세대로 재귀호출을 할 때는 이전세대의 끝점의 좌표를 다음세대로 전달하면서 호출해야한다.
사실 우리는 회전시킨 좌표와 기존좌표를 연결할 때 끝점의 좌표를 알 수 있었다. 좌표를 회전시킬때 항상 시작점을 축으로 삼으며 회전시킨다.즉 끝점은 항상 (0,0)과 가장 멀리떨어진 곳이다. 따라서 회전시킨 좌표에서 0,0이었던 부분이 기존좌표에 연결되기 위해 이동하면 이것이 현재세대의 가장 끝점이 된다는 것이다.
위의 예시에선 (0,0)+(0,-2) = (0,-2)가 현재세대의 끝점이 된다는 것이다.
위와같은 패턴으로 다음세대의 그림이 어떻게 되는지 구해보는 과정은 다음과같다
1. (0,0) (0,-2) (0,-1) (1,-1) (1,0)이 각각 (x,y)라 했을 때 (-y,x)를 구해보면
(0,0) (2,0) (1,0) (1,1) (0,1)이 된다.

- 이때 이전세대에서 끝점이었던 0,-2가 2,0으로 옮겨졌기 때문에 (0,-2) - (2,0) = (-2,-2)만큼 모든 좌표를 이동해 이전세대와 합친다. 그러면 좌표는 (-2,-2) (0,-2) (-1,-2) (-1,-1) (-2,-1)이 된다.

- 이좌표들을 기존좌표에 추가시키고 (0,0)은 (-2,-2)로 이동되었으므로 (-2,-2)를 끝점좌표로 다음 세대에 전달한다.
이런식으로 n = g가 될때까지 반복한다. 코드로 나타내면 다음과같다.
#include <iostream>
#include <vector>
using namespace std;
int N;
int x, y, d, g;
int arr[101][101];
void dragon_curve(int n,vector<pair<int,int>>xy,int end_x,int end_y) { //드래곤 커브 그리기
if (n == g) {
return;
}
vector<pair<int, int>>plus = xy; // xy에 추가될 좌표
int plus_end_x; //추가된 좌표중 끝점좌표
int plus_end_y;
for (int i = 0; i < xy.size(); ++i) { (x,y)를 (-y,x)로 바꿔 90도 회전
int X = xy[i].first;
int Y = xy[i].second;
plus[i].first = -Y;
plus[i].second = X;
if (X == end_x && Y == end_y) {
plus_end_x = plus[i].first;
plus_end_y = plus[i].second;
}
}
int dif_x = end_x - plus_end_x;
int dif_y = end_y - plus_end_y;
for (int i = 0; i < plus.size(); ++i) { //기존좌표와 추가된 좌표의 끝점을 연결해 합치기
plus[i].first = plus[i].first + dif_x;
plus[i].second = plus[i].second + dif_y;
if (plus[i].first == end_x && plus[i].second == end_y) {
continue;
}
int map_x = plus[i].first + x;
int map_y = plus[i].second + y;
if (map_x >= 0 && map_y >= 0 && map_x < 101 && map_y < 101) {
arr[map_y][map_x] = 1;
}
xy.push_back(make_pair(plus[i].first, plus[i].second));
}
dragon_curve(n + 1, xy, plus[0].first, plus[0].second);
}
void input() {
cin >> N;
for (int i = 0; i < N; ++i) {
cin >> x >> y >> d >> g;
vector<pair<int, int>>xy;
arr[y][x] = 1;
xy.push_back(make_pair(0, 0)); // 0세대 드래곤커브 만들기
if (d == 0) {
xy.push_back(make_pair(1, 0));
if (x + 1 < 101) {
arr[y][x + 1] = 1;
}
}
else if (d == 1) {
xy.push_back(make_pair(0, -1));
if (y - 1 >= 0) {
arr[y - 1][x] = 1;
}
}
else if (d == 2) {
xy.push_back(make_pair(-1, 0));
if (x - 1 >= 0) {
arr[y][x - 1] = 1;
}
}
else if (d == 3) {
xy.push_back(make_pair(0, 1));
if (y + 1 < 101) {
arr[y + 1][x] = 1;
}
}
dragon_curve(0, xy, xy[1].first, xy[1].second);
}
}
void get_cnt() {
int cnt = 0; //사각형 갯수세기
for (int i = 0; i < 100; ++i) {
for (int j = 0; j < 100; ++j) {
if (arr[i][j] == 1 && arr[i + 1][j] == 1 && arr[i][j + 1] == 1 && arr[i + 1][j + 1] == 1) {
++cnt;
}
}
}
cout << cnt;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
input();
get_cnt();
}
