Medical Image Segmentation - Active contour model

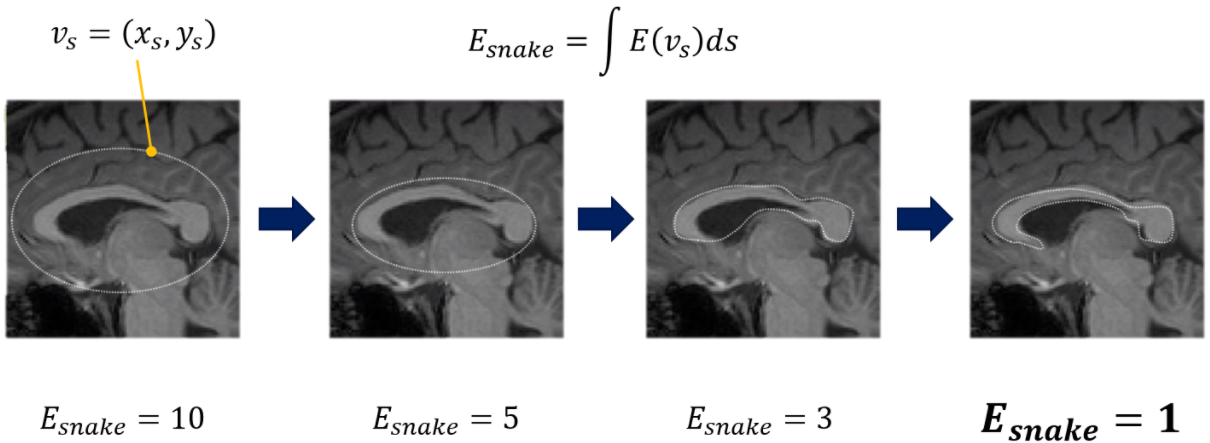
1. Active Contour Model

Active contour model은 foreground의 contour $v_s=(x_s,y_s)$를 점차 업데이트 하면서 energy function $E=\int E(v_s)ds$를 최소화 하는 contour를 찾는 것을 목표로 한다.

2. Snake Energy Function

이 때 contour의 경계가 업데이트 되는 모습이 마치 뱀과 같이 구불구불하다고 해서 energy function은 snake energy function이라고 불린다.

Snake energy function은 그 때 그 때 사용자의 목적에 따라 다르게 정의할 수 있으며 일반적으로 아래와 같이 external energy term과 internal energy term으로 나뉘어 정의되며 각각 세부적으로 또 나뉜다.

$E_{snake}=E_{external}+E_{internal}=(E_{line}+E_{edge})+(E_{elastic}+E_{bending})$

1) External Energy Term

• Case 1: Line Energy

  

  Line energy term은 foreground의 boundary의 line에서 구분되는 값이 있을 것이라 가정하여 energy function을 정의한다.
  만약 line energy term을 $E_{line}=I(x)$로 정의하면, contour가 black line을 따라 위치 했을 때 $E_{line}$이 가장 작은 값을 갖게 된다.

• Case 2: Line Energy

  

  반면, 동일하게 boundary의 line에서 구분되는 값이 있을 것이라 가정하고 line energy term을 $E_{line}=-I(x)$로 정의하면, contour가 white line을 따라 위치해 있을 때 $E_{line}$이 가장 작은 값을 갖게 된다.

• Case 3: Edge Energy

  

  경계가 뚜렷한 곳에서 boundary가 생길 것이라 가정하고 정의한 energy term을 edge energy term이라고 한다. Energy function을 위 그림의 식과 같이 정의하면 $x$, $y$의 변화량의 절대값이 클 수록, energy function이 작은 값을 갖게 된다.

2) Internal Energy Term

• Case 1: Elastic Energy

  

  Elastic energy term은 target boundary의 shape이 굴곡이 별로 없다는 것을 알고 있을 때 효과적인 energy term이다.

  위 그림의 식과 같이 각 pixel value의 $v_s$를 1차 미분한 $V_s$에 가중치를 곱한 값의 합으로 정의한다.

  그 결과, elastic energy function을 최소화하기 위해, 오른쪽 그림처럼 굴곡진 부분이 평평하게 변형되는 효과를 얻을 수 있다.

• Case 2: Bending Energy Term

  

  Bending energy term은 target boundary의 shape에 뾰족한 부분이 별로 없다는 것을 알고 있을 때 효과적인 energy term이다.

  위 그림의 식과 같이 elastic energy term의 1차 미분값 $V_s$를 한번 더 미분한 2차 미분값 $V_{ss}$에 가중치를 곱한 값의 합으로 정의한다.

3) Snake Energy Function

Snake energy function은 위 term들을 모두 합친 형태가 된다. 식은 다음과 같다.

$E_{snake}=\int E_{snake}(v_s)ds$

$\ \ \ \ \ \ \ \ \ \ \ \ =\int (E_{external}(v(s))+E_{internal}(v(s)))ds$

$\ \ \ \ \ \ \ \ \ \ \ \ =\int (I(x)-|\nabla I(x,y)|^2+\frac{1}{2}\alpha_s|V_s|^2+\frac{1}{2}\beta_s|V_{ss}|^2)ds$