[AI Math] 행렬?

행렬

• 행렬이란 벡터를 원소로 가진 2차원 배열이다.

• 위와 같이 행(row)벡터가 모인 배열, 혹은 열(column)이 모인 배열로 볼 수 있다.

• python에서는 행벡터를 원소로 가진 배열로 이해하면 코드작성이 수월하다.

• 보통 벡터는 소문자 볼드체로 표현하고 행렬은 대문자 볼드체로 표현한다.

• 행렬의 원소는 $x_{ij}$와 같이 표기하는데 앞의 $i$는 행, $j$는 열을 나타낸다.

전치

• $X^T = (x_{ji})$

• 행과 열이 바꾸는 연산이다.

• n개의 행과 m개의 열이였다면 m개의 행과 n개의 열로 바뀌게 된다.

공간상의 행렬

• 전 시간에 벡터는 공간상에서 한 점으로 표현할 수 있다고 배웠다.

• 따라서, 행렬은 여러 점(데이터)의 집합으로 이해할 수 있다.

행렬의 덧셈, 뺄셈, 성분곱, 스칼라곱

행렬의 덧셈과 뺄셈, 성분곱

• 두 행렬($X,Y)$가 같은 모양(shape)라면 element wise로 연산이 이루어진다.

• 스칼라 곱 연산도 벡터와 차이가 없다.

행렬의 곱셈

• 두 행렬($X, Y$)의 $i$번째 행벡터와 $j$번째 열벡터의 내적으로 계산된다.

• 위와 같은 연산을 위해서는 $X$의 열과 $Y$의 행의 크기가 같아야 한다.

• $X,Y$의 순서에 따라 결과가 달라지기 때문에 주의해야 한다.

• numpy에서는 X @ Y 로 연산이 가능하다.

• numpy.inner함수는 $X$와 $Y^T$를 연산한 결과이다.

• numpy.inner함수는 $X$의 행의 개수와 $Y$의 행의 개수가 같을때 사용한다.

행렬의 이해하는 다른 방법

• 행렬은 하나의 연산자(operator)로 이해할 수 있다.

• 선형대수에서는 선형변환이라고 불리는 연산을 담당한다.

• 벡터 $x$에 $A$라는 행렬을 취함으로 새로운 차원의 $z$로 변환시킬 수 있다.

• $m$차원 (3차원 x)를 $n$차원 (2차원 z)공간으로 보낼 수 있다.

역행렬

• 어떠한 행렬 $A$의 연산을 되돌리는 행렬을 역행렬(inverse matrix)라 부르고 $A^{-1}$이라 표기한다.

• $AA^{-1} = A^{-1}A = I$

• $I$는 항등행렬로 어떤 행렬과 항등행렬과의 행렬곱은 결과는 항상 자기 자신이다.

• 역행렬을 위와 같이 $m$차원을 $n$차원으로 이동시킨 $A$연산을 다시 $m$차원으로 되돌린다.

• 역행렬은 행과 열의 개수가 같아야 하며, 행렬식(determinant)이 0이 아니여야 한다.

• numpy.linalg.inv로 계산할 수 있다.

• 만일 역행렬을 계산할 수 없다면 유사역행렬(무어-펜로즈 역행렬)을 사용하며 $A^+$로 나타낸다.

• $n$은 행, $m$은 열을 나타낸다.

• $A^+A=I$가 성립한다.

• numpy.linalg.pinv로 계산할 수 있다.

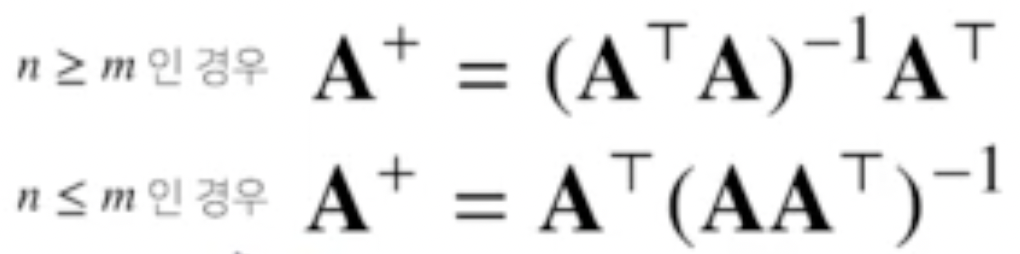
주의
만약 행이 열보다 많게 되면 원래행렬보다 먼저 곱해줘야 항등행렬을 구할 수 있다.

• 선형회귀에서도 의사역행렬을 사용하여 $\beta$값을 구한다.

• 방정식을 완벽하게 푸는것이 아닌 최대한 합리적인 값을 구하게 된다.

$X\beta=y$일때, $\beta = X^+y$로 접근할 수 있으며
$\hat{y}, y$간의 L2 norm의 차이를 최소화 하는 방향으로 선형회귀식을 구할 수 있다.