Attention is all you need, NeurIPS
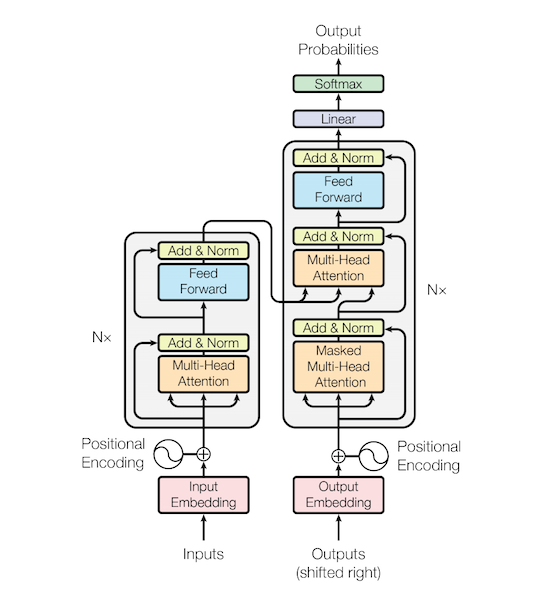
주어진 sequence에 대해 encoding하는 RNN을 대체하는 용도로 Transformer의 구조와 작동 방식을 알아보기.
Self Attention
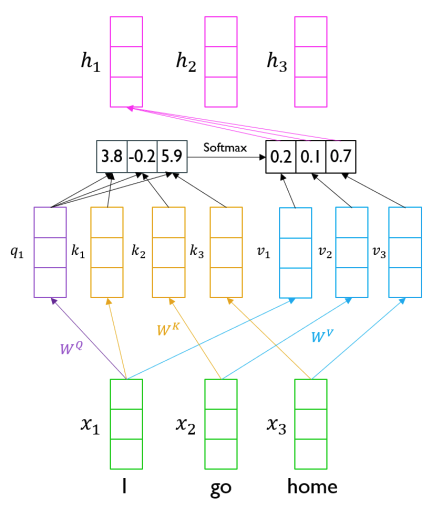
Transformer도 input 각각에 대해서 인코딩한 encoding vector 를 생성하는 구조로 이해할 수 있다. 다만 기존의 RNN구조와 다른 방식으로 만들어내는데 이 방식을 Self Attention이라고 부른다.
앞서 Sequence to Sequence with attention에서 decoder의 hidden vector가 encoder의 hidden vectors와의 유사도를 통해 Attention이 진행되었던것과 유사하게 진행이 된다. 위의 이미지에서 I를 decoder의 hidden state라고 생각을 하고 I, go, home 전체가 encoder의 hidden states로 생각할 수 있다. 따라서 I와 I, go, home간의 내적과 softmax를 한 score를 입력과의 선형결합을 통해 가중평균을 구할 수 있다. 이와 같은 계산을 입력 단어 전체에 해주어 각각의 hidden vector들을 구하게 된다.
이처럼 단순히 내적을 통해 확률로 변환한다면 I는 I와, go는 go와 가장 높은 유사도를 나타낼 것이며 이 말은 단순히 자기 자신의 정보를 많이 가진 벡터가 될것이다. 따라서 Transformer에서는 내적을 하기전 hidden state를 선형변환한 값(을 사용하게 된다.
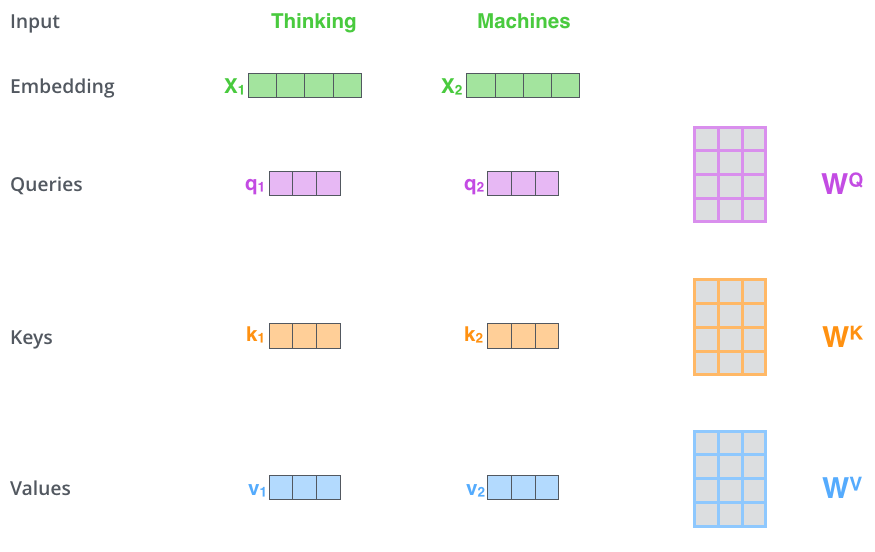
Transforemr에서는 Query, Key, Value라는 3가지 벡터가 존재한다.
Query는 유사도를 구할때 주어진 벡터들 중 어떤 벡터들을 가져올지를 기준이 되는 벡터이다. Key는 Query와 유사도를 계산하기 위한 재료벡터들이며 그렇게해서 구한 유사도를 통해 구한 가중치를 적용하여 가중편균을 구하게 되는 벡터를 Value라고 부른다.
I go home을 예로 들면 I에 대한 hidden state를 구한다고 하면 query는 I가 된다. 이 I와 내적하게 될 I, go, home이 key가 되고 이렇게 구한 유사도를 적용시킬 I, go, home이 value가 된다. 현재는 key와 value에 적용되는 대상이 같지만 Transformer의 decoder에서는 달라지기 때문에 주의해야한다.
위와 같이 각각 사용되는 목적에 따라 선형변환을 통해 구하게 되는데 이같은 방법으로 I가 자신 I와의 유사도가 높아지는 것을 방지할 수 있다.
여기서 중요한점은 기존의 RNN에서 보이던 한계점인 time step이 멀면 정보를 가져오기 힘들다는 것을 해결할 수 있었다. 아무리 긴 sequence를 가졌다 하더라도 내적의 값이 크다면 time step이 멀더라도 손쉽게 정보를 가져올 수 있다.
query벡터 자체도 다수로 확장한 형태에 대한 수식은 아래와 같다.
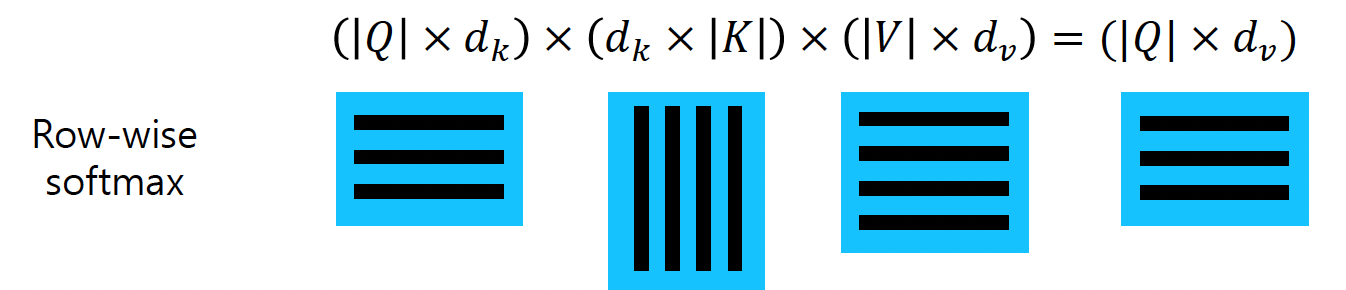
Scaled Dot-Product Attention
Transformer에 위의 수식을 사용할때 로 scaling을 해준다.
하나의 와 의 내적값은 언제나 스칼라값을 나타내지만 이 계산에 참여하는 차원은 1차원, 2차원 혹은 수백 차원으로 정의 될 수 있다.
가령 2차원을 가지는 와 를 생각해 봤을때 의 형태로 스칼라 값이 정의 된다. 각각의 원소()를 어떤 평균과 분산을 갖는 확률변수(random variable)로 생각해볼 수 있다. 각각을 평균을 0, 분산을 1로 갖는 확률변수로 가정할때 의 평균은 0, 분산은 1, 도 평균은 0, 분산은 1의 값을 갖는다. 이에 대한 증명은 통계학에 정의되어 있다고 한다. 결과적으로 의 평균은 0이지만 분산은 2로증가하게 된다.
따라서 q와 v가 100차원이라면 분산이 100이 되는것을 알 수 있다. 극단적으로 2차원일때의 표준편차가 이고 100차원일때 표준편차는 일때 각각 출력값에 softmax를 취하면 표준편차가 클수록 한 key에 확률값이 몰리는 분포를 가지며 낮을수록 고른 분포를 갖게 된다.
이런 상황을 방지하기 위해 를 연산을 추가하여 차원에 상관없이 분산을 1로 유지할 수 있게 된다.