optimizer

• SGD (Stochastic Gradient Descent)
• Momentum
• NAG (Nesterov Accelerated Gradient)
• AdaGrad
• RMSProp
• AdaDelta
• Adam

SGD (Stochastic Gradient Descent)

$W = W - (lr * \frac{dL}{dW})$
$lr = Learning$ $rate$

- BGD(Batch Gradient descent)는 전체 데이터셋에 대한 에러를 구한 후 기울기를 한번만 계산하여 parameter를 업데이트 하는 방법이다.
여기서 말하는 Batch는 전체 훈련 데이터셋을 의미한다.

장점)
전체 데이터에 대해 업데이트가 한번에 이루어지기 때문에 전체적인 계산횟수가 적다.
병렬처리에 유리하다.

단점)
한 스텝에 모든 데이터를 사용하므로 학습이 오래 걸린다.
전체 학습 데이터에 대한 에러를 모델의 업데이트가 이루어지기 전까지 축적해야 하므로 메모리 소모가 크다.
local optimal에 빠질 위험이 크다.

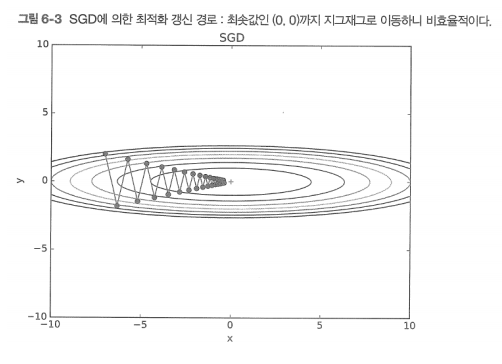
- SGD는 추출된 데이터 한개에 대해서 에러를 계산하고 gradient descent를 적용하는 방법이다.
SGD의 장점은 local optimal에 빠질 위험이 적으며 step에 걸리는 시간이 짧아 수렴속도가 빠르다.
단점으로는 global optimal을 찾지 못할 수 있으며 데이터를 한개씩 처리하기 때문에 GPU 성능을 전부 활용할 수 없다.

- MSGD(mini-batch SGD)
SGD와 MSGD는 다른 알고리즘이지만 최근에는 SGD를 MSGD로 사용하곤 한다.
MSGD는 BGD와 SGD의 장점을 모아 만든 방법으로, 전체 데이터에서 뽑은 mini-batch안의 데이터 n개에 대해서
각 기울기 n을 구한 후, 그것의 평균 기울기를 통해 모델을 업데이트하는 방법이다.

Momentum (GD with momentum)

$v_t = \alpha v_{t-1} - (lr * \frac{dL}{dW})$
$W = W + v$

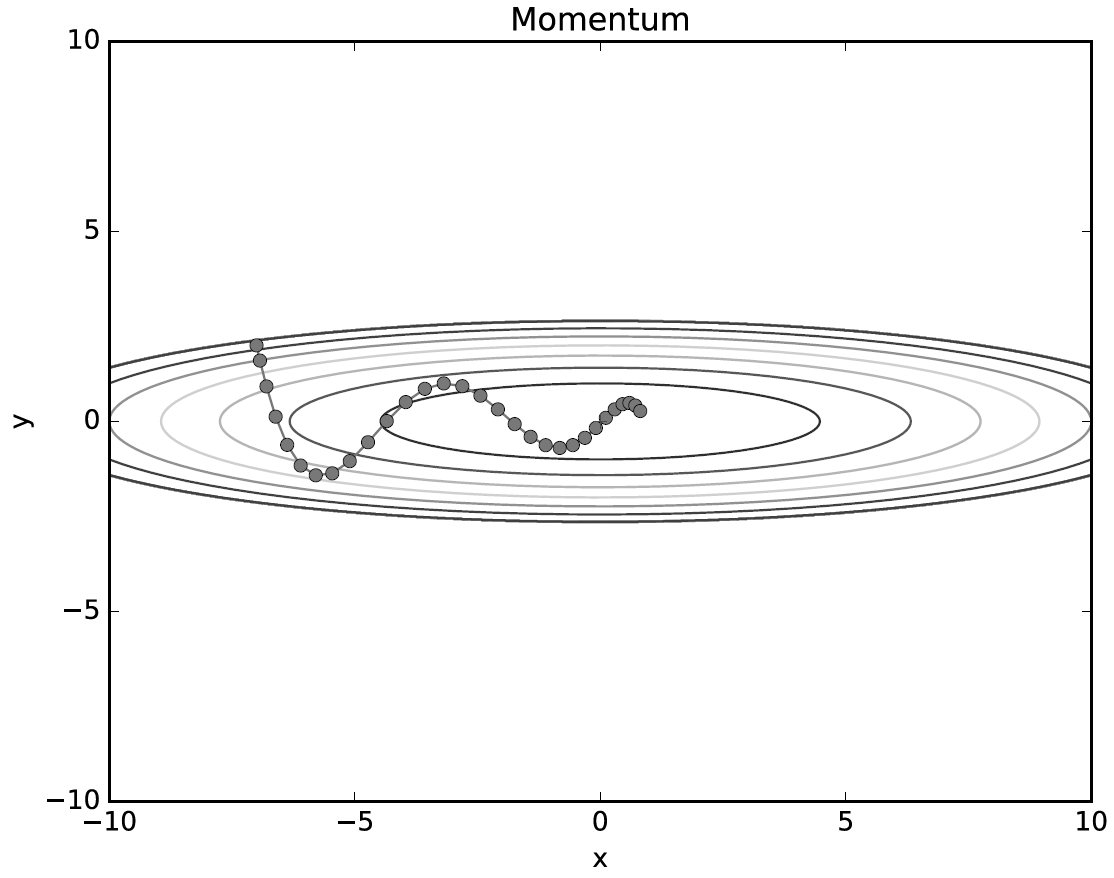
모멘텀은 기본적인 $lr * grads$에 운동량을 개념을 도입한 경사하강법이다.
이동하는 방향과는 별개로 과거에 이동했던 방식을 기억하며 그 방향으로 일정 정도를 추가적으로 이동하는 방식(가속도를 구현한 것)
속도라는 개념을 추가해 local minima에 빠지지 않도록 함.

장점 : 가속도라는 개념으로 local optimal에 탈출하기 쉽다.
단점 : 가속도라는 개념으로 적절한 global optimal에도 작용하여 최소값을 벗어나는 일이 생길 수 있다.

NAG

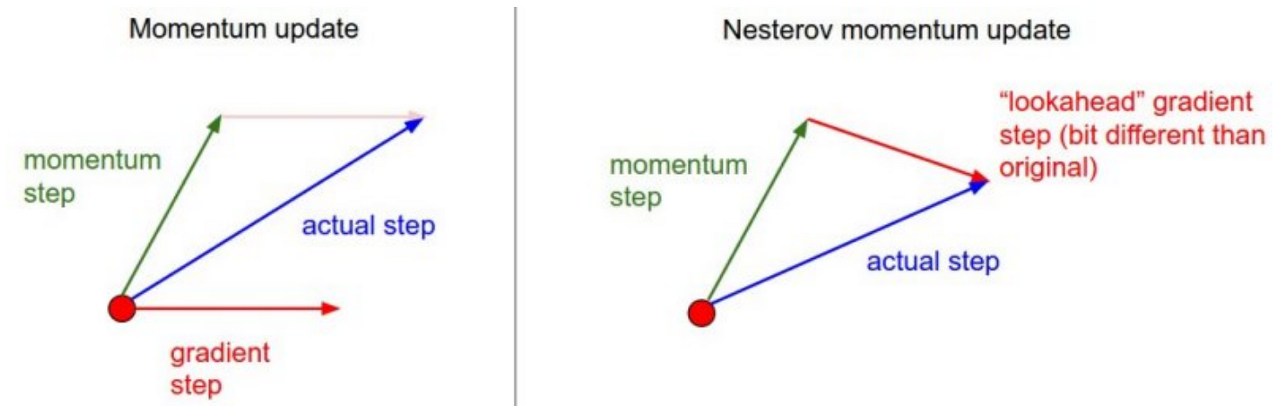
Momentum 방식을 개선한 것으로, momentum의 경우 grads를 구하고 가속도를 모멘텀 계수와 곱하여 이 값을 서로 더해주는 방식이다.

NAG(Nesterov Accelerated Gradient)는 운동량에 따른 변화를 먼저 적용시키고 그 후에 그것에 대한 grads를 구하여 갱신 시킨다.

$v_t = \alpha * v_{t-1} - lr * \partial _{W} L(W_t + \alpha * v_{t-1})$
$W_t = W_{t-1} + v_{t}$

장점 : 운동량을 적용시키는 시점이 기울기를 정하는 시점이므로 기존 모멘텀의 단점인 최적점에서도 지나쳐버리는 단점을 해결 할 수 있다.

AdaGrad

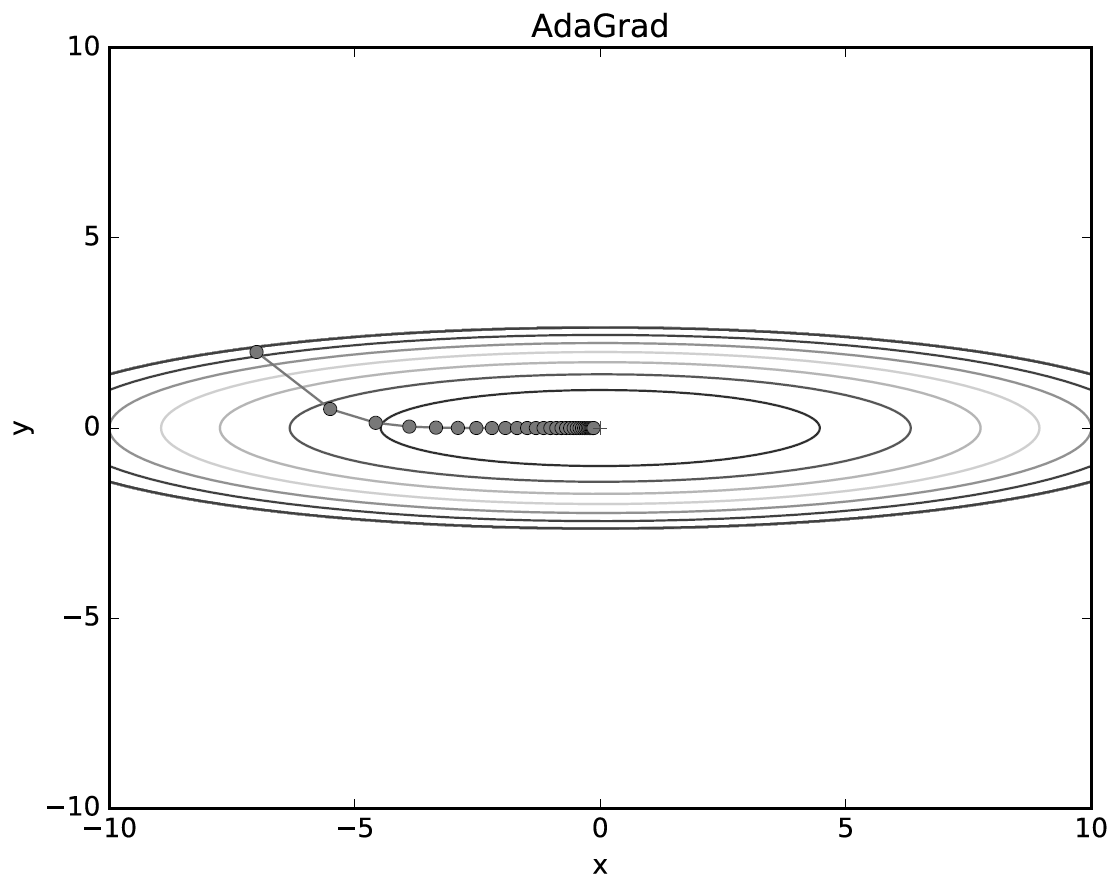
AdaGrad는 adaptive gradient optimizer의 약자이다.
적응형 옵티마이저란 각 변수들에 대해 learning rate가 따로 적응하여 작용하는 것을 의미한다.

gloabal learning rate를 사용하게 되면 큰 갱신이 필요한 파라미터의 경우 비교적 작게 변화하고,
작은 갱신이 필요한 경우 상대적으로 크게 변화하게 될 것이다. 따라서 파라미터별로 다른 learning rate를
적용시켜야 하며 이 기능을 하는 것이 AdaGrad이다.

$h = h + \frac{\partial L}{\partial W} * \frac{\partial L}{\partial W}$

$W = W - lr * \frac{1}{\sqrt{h}} * \frac{\partial L}{\partial W}$

여기서 $h$는 기울기를 제곱을 해줌으로 방향이 아니라 얼마나 움직였는가에 대한 크기를 반영하기 위한 것이다.
가중치 변화의 정도가 컸던 파라미터에 대해서는 그 학습으로 최적점에 도달했을 가능성이 높다고 판단하고 점차 가중치를 줄이는 기준으로 삼는 것이다.
이것의 역수를 사용해 학습률에 제한을 두는 방법이다.

$h$값이 커질 수록 lr값이 0에 가까워지기 때문에 의미를 상실하여 학습을 멈추는 경우도 발생한다.
이 경우는 기울기 소실과 다르며 기울기가 존재함에도 lr이 작아져 학습이 멈춰버리는 현상이다.

RMSProp

AdaGrad를 개선한 방식으로 학습률 소실문제를 해결하기 위한 방안으로 나왔다.
RMS는 Root mean Square약자로 AdaGrad의 root square에 가중평균 mean의 개념을 도입했다.

$h = ph + (1-p)\frac{\partial L}{\partial W} * \frac{\partial L}{\partial W}$

p값은 하이퍼파라미터로 그 값이 작아질수록 최신의 기울기에 더 큰 영향을 받게 된다.
이 값은 보통 0.9로 설정하는게 좋다고 알려져 있다. (기존 기울기에 90프로 영향, 새로운 기울기에 10프로 영향)

Adam

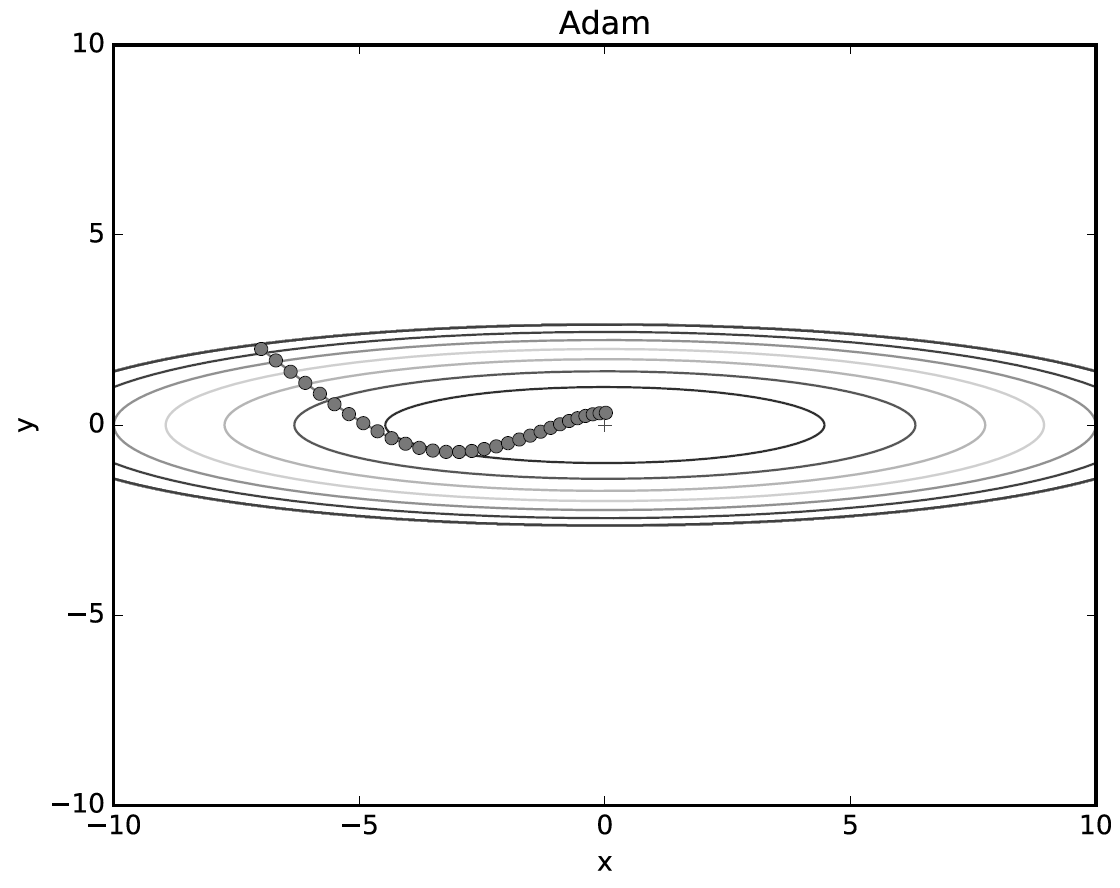
Momentum(관성이용)과 AdaGrad(lr 조절)를 융합한 방법이다.
Adam은 두 기법에서 $v$와 $h$가 최초 0으로 설정되어 학습 초반에 0으로 biased되는 문제를 해결하기 위해 고안한 방법이다.

• Momentum (지수평균 사용)
  $v = p*v + (1-p)*\frac{\partial L}{\partial W}$
  

• RMSProp
  $h = p*h + (1-p)\frac{\partial L}{\partial W} * \frac{\partial L}{\partial W}$

여기에 아래와 같이 편향보정을 해준다.

$vc = v/(1-p^t)$
$hc = h/(1-p^t)$

$W = W * lr * vc / \sqrt{sc} + epslion$