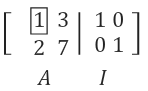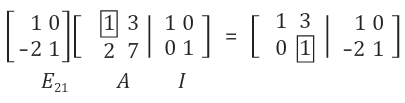모든 자료는 이곳에서 출처를 둠
지난 시간에 배운 행렬의 곱셈에 대해서 좀 더 자세히 알아보고 역행렬이 무엇이며 어떻게 구하는지 알아보자.
행렬 곱셈 ( Matrix multiplication )
1. row * column
⎣⎢⎡a31a32a33a34⎦⎥⎤⎣⎢⎢⎢⎡ b12 b22 b32 b42 ⎦⎥⎥⎥⎤=⎣⎢⎡ c32⎦⎥⎤
A B C
3X4 4X3 3X3
(m x n) (n x p) (m x p)
row * column의 관점에서 볼 때, C의 c32원소는 A의 3번째 row와 B의 2번째 column의 곱으로 만들어진다. 이런 연산과정을 우리는 내적(dot product)라고 말한다.
A의 3번째의 row요소들과 B의 2번째 column요소들이 각각 원소들과 곱해지고 더 해지는 과정을 거친다.
c32=a31b12+a32b22+a33b32+a34b42
이 연산을 하기 위해서는 A행렬의 열의 수(n)와 B행렬의 행의 수(n)이 반드시 같아야 가능한 연산인 것을 알 수 있다.
또한 결과적으로 C행렬의 형태는 (A행렬의 행xB행렬의 열)의 형태로 나오는 것을 볼 수 있다.
이 과정이 우리가 보통 행렬을 수식으로 계산할 때 사용하는 방법이다.
2. column-wise
행렬의 곱을 전 시간에 다룬 ( matrix * column )의 관점으로 볼 수 있다.
⎣⎢⎡a11a21a31a12a22a32a13a23a33a14a24a34⎦⎥⎤⎣⎢⎢⎢⎡b11b21b31b41b12b22b32b42b13b23b33b43⎦⎥⎥⎥⎤=⎣⎢⎡c11c21c31c12c22c32c13c23c33⎦⎥⎤
⎣⎢⎡a11a21a31a12a22a32a13a23a33a14a24a34⎦⎥⎤⎣⎢⎢⎢⎡b11 b21 b31 b41 ⎦⎥⎥⎥⎤=⎣⎢⎡c11c21c31⎦⎥⎤
⎣⎢⎡a11a21a31a12a22a32a13a23a33a14a24a34⎦⎥⎤⎣⎢⎢⎢⎡b11b21b31b41⎦⎥⎥⎥⎤=b11⎣⎢⎡a11a21a31⎦⎥⎤+b21⎣⎢⎡a12a22a32⎦⎥⎤+b31⎣⎢⎡a13a23a33⎦⎥⎤+b41⎣⎢⎡a14a24a34⎦⎥⎤=⎣⎢⎡c11c21c31⎦⎥⎤
C행렬의 첫번째 열은 A행렬의 column들의 조합이라는 것을 알 수 있다.
3. row-wise
행렬의 곱을 전 시간에 다룬 ( row * matrix )의 관점으로 볼 수 있다.
⎣⎢⎡a11a21a31a12a22a32a13a23a33a14a24a34⎦⎥⎤⎣⎢⎢⎢⎡b11b21b31b41b12b22b32b42b13b23b33b43⎦⎥⎥⎥⎤=⎣⎢⎡c11c21c31c12c22c32c13c23c33⎦⎥⎤
⎣⎢⎡a21a22a23a24⎦⎥⎤⎣⎢⎢⎢⎡b11b21b31b41b12b22b32b42b13b23b33b43⎦⎥⎥⎥⎤=⎣⎢⎡c21c22c23⎦⎥⎤
⎣⎢⎡a21a22a23a24⎦⎥⎤⎣⎢⎢⎢⎡b11b21b31b41b12b22b32b42b13b23b33b43⎦⎥⎥⎥⎤
=a21[b11b12b13]+a22[b21b22b23]+a23[b31b32b33]+a24[b41b42b43]
=[c11c12c13]
C행렬의 row들은 B행렬의 row들의 조합으로 이루어진다.
4. column * row
맨 처음에 살펴보았던 row * column과 순서가 반대이다.
(column of A) x (row of B) ⇢ ⎣⎢⎢⎢⎡2−1:4⎦⎥⎥⎥⎤ x [32…6]
(m x 1) (1 x p)
이 계산의 결과는 m x p의 행렬이 된다.
계산 결과를 알아 보기 위해 row-wise나 column-wise의 관점에서 보면
A의 원소가 B의 row와 곱하여 더해지거나, B의 column원소가 A에 곱하여 더해지는 것을 상상하면 쉽게 알 수 있다.
column * row의 관점은 A의 column들과 B의 row들의 행렬곱의 합이다.
각각의 column과 row의 결과는 full_size결과를 나타내고 이 full_size결과가 총 n개 생긴 것들의 합이다.
여기서 중요한 부분이 있다.
⎣⎢⎡234⎦⎥⎤[16]=⎣⎢⎡234121824⎦⎥⎤
A B C
위 처럼 column * row의 형태에서 중요한 규칙이 있다.
row-wise관점에서 봤을 때, C의 row벡터들은 B벡터를 따라 같은 line에 위치한다.
column-wise관점에서 봤을 때, C의 column벡터들은 A벡터를 따라 같은 line에 위치한다.
C의 rank ( 선형독립인 row나 column의 수)가 1인 것을 알 수 있다.
조금만 생각해보면 A벡터의 상수배를 하여 벡터의 크기를 줄이거나 늘릴 뿐 방향이 바뀌지는 않는다.
마찬가지로 B벡터에 상수배를 한 것일 뿐 방향을 바꿔주는 것은 아니다.
결국 어떠한 벡터이건 column*row인 경우는 이런 특별한 행렬이 만들어지게 된다.
역행렬
선형변환
우리는 역행렬을 정확히 이해하기 위해 선형변환이란 용어부터 정리하고 갈 필요가 있다.
[acbd][xy]=[ef]
A x= b
이 Ax=b라는 형태에서 A행렬은 선형변환의 역할을 한다.
변환인라는것은 우리에게 익숙한 말로는 함수라고 표현할 수 있다.
어떤 input을 변환(함수)를 통해 ouput으로 표현하는 것 이다.
선형대수에서 이 함수를 변환이라고 표현하는 이유는 시각적으로 생각해보면 알 수 있다.
xy평면에서 x축에 대한 벡터 [10] 기저 벡터( i^, i햇 )라고 부른다.
y축에 대한 벡터 [01]도 기저 벡터( j^, j햇 )라고 부른다.
xy평면에서 이 두 개의 벡터로 모든 벡터를 표현할 수 있다.
[1001][11]
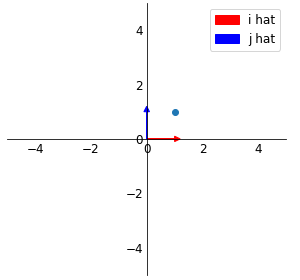
위의 행렬은 단위벡터로 이루어져 있기 때문에 input데이터는 그대로 유지가 된다.
[1231][11]
그렇다면 위의 행렬로 선형변환이 이루어진다면 새로운 기저 벡터로 공간이 변환 된다.
inew^=[12]
jnew^=[31]

위의 그림처럼 새로운 기저벡터로 공간이 변환된다. 공간이 변환되면서 원점은 그대로 이며 모든 그리드는 똑같은 간격을 유지해야 선형변환이 된다. 비교를 위해 위의 그림의 배경에는 기존 그리드를 유지시켰으니 상상을 하면서 보면 이해가 된다. ( 원래 1,1의 격자를 유지 하던 공간이 커진 것으르 알 수 있다. )
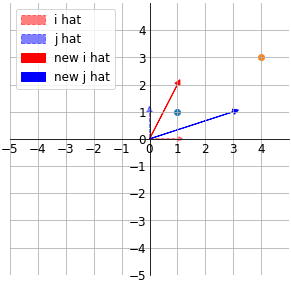
공간이 변환되면서 기존에 x벡터는 [41]로 이동된다.
변환되기 전의 기저벡터에서 x벡터는 기저벡터들의 1배씩 곱하여 더한 값에 위치해 있었다.
자세히 보면 변환되고 난 기저벡터에서도 똑같이 1배씩 곱하여 더한 값에 위치해 있다.
선형변환에서 시각적으로 가장 중요한 것은 공간이 변환된다는 것을 알아야 한다.
그렇다면 역행렬이란 무엇일까 ? 역행렬의 특징을 알아보기 전 기하학적 의미부터 알고 가자.
위에서 처럼 어떠한 선형변환이 이루어졌을 때 역행렬은 이 변환을 다시 원상태로 복구시킬수 있는 또다른 선형변환을 의미한다. A라는 선형변환을 통해 공간을 좌측으로 90도 회전 했다고 상상해보자. 그럼 이 A는 무엇이 될까 ?
[01−10][11]
A x

위 처럼 공간이 좌측으로 90도 회전했을 때 이 행렬의 역행렬은 무엇일까?
자연스럽게 우측으로 90도를 회전시키면 될 것이다.
[0−110]
이 새로운 선형변환을 적용시키면 다시 원래자리로 돌아올 수 있다.
역행렬이 가지고 있는 의미는 이렇게 다시 복구할 수 있는 선형변환이 존재하느냐 이다.
그럼 역행렬이 없다는 것은 다시 복구할 수 있는 선형변환이 없다는 말인데 그런 경우가 무엇일까?
선형변환의 결과로 2차원이 1차원으로 뭉개지면 그 것을 다시 복구시킬 행렬은 없다.
3차원에서도 마찬가지로 선형변환의 결과가 평면, 선으로 뭉개지면 복구시킬 수 없다.
- Invertible(역행렬이 있는), non-singular(비특이행렬)
어떤 A라는 행렬이 역행렬이 존재한다고 가정할 때,
A−1A=I=AA−1
위와 같은 특징을 가지고 있다. ( I는 단위행렬 )
행렬의 곱셈에서 교환법칙이 성립하지 않는다는 것을 알고 있는데 앞에서 곱한 결과와 뒤에서 곱하는 결과가 같은 것을 볼 수 있다. (선형변환 후 다시 원상복구)
일반 행렬의 경우 교환법칙이 성립하지 않지만 정방행렬의 경우 결과가 같다.
- non-invertible, singular
이제 역행렬이 존재하지 않는 경우를 살펴본다. 이런 행렬을 singular matrix(특이행렬)이라고 부른다.
[1236] A
위의 행렬 A는 역행렬이 존재하지 않는 경우이다.
그 이유를 알아보자.
- 행렬식(determinant, 2차원일 때)
행렬A(2차원일 때)의 행렬식의 값은 0이 된다. 따라서 역행렬이 존재하지 않는다.
그렇다면 행렬식이 의미하는 것은 무엇일까?
결론부터 말하면 2차원에서는 넓이의 증감, 3차원에서는 부피의 증감을 나타낸다.
선형변환은 하기 전 단위벡터로 이루어진 넓이 ( 격자의 넓이, 1 )이 선형변환 후
새로운 기저벡터로 이루어진 넓이 ( 변환 후 격자의 넓이 )가 얼마나 증가했는지, 감소했는지를 나타낸다.
[2002]
위의 행렬식의 값은 4이다. 이 4가 의미하는 것이 무엇일까?
a x d는 아래의 빨간색 정사각형의 넓이를 나타낸다.
주황색 범위의 넓이 ( 단위벡터로 이루어진 )가 4배 증가한것을 알 수있다.
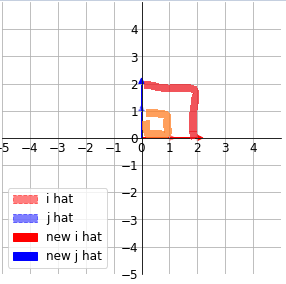
[2012]
위의 행렬식의 값도 4이다.
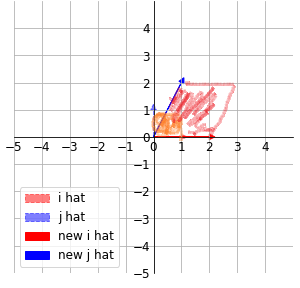
a x d는 기하학적으로 평행사변형의 넓이를 나타낸다.
[acbd]
그렇다면 a, b, c, d전부 0이 아닌 값을 가지고 있을 때는 어떻게 이해할 수 있을까?
위의 행렬식은 0이 될수도 안될수도 있다.
행렬식이 0이 된다는 것은 같은 새로운 기저벡터들이 평면을 이루지 못하고 같은 line에 존재하는 경우이다.
행렬식의 값이 0 이 아닌 경우에 bc가 의미하는 것은 무엇일까?
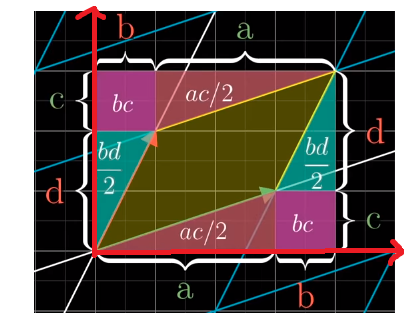
새로운 기저벡터로 이루어진 평행사변형의 넓이를 구하기 위하기 위해 큰 직사각형에서
여러가지 도형의 넓이를 빼보면 ab-bc의 값을 얻을 수 있다.
3차원에서는 부피의 증감으로 다가갈 수 있다.
이 부분을 이해하면 아래에서 설명할 column vector에 대해서 쉽게 이해할 수 있다.
- column vector
[12] [36]
행렬A의 열벡터를 봤을 때 이 벡터들이 선형종속의 관계에 있는 것을 볼 수 있다. 즉 같은 line에 위치하는 벡터이다. A의 rank는 1이며 선형 독립인 차원의 개수가 열벡터의 차원보다 작기 때문에 특이행렬이 된다. 따라서 행렬 A의 역행렬은 존재하지 않는다.
기하학적인 이해로 같은라인에 있으면 행렬식의 값이 0이 될 수 밖에 없다는 것을 알 수 있다.
3. Ax=0
만약 Ax=0을 만족하는 벡터 x를 찾을 수 있다면, 역행렬이 존재하지 않는다.
(이때 A는 정방행렬, x는 0이 아닌 벡터)
이 말이 무슨 의미를 가지는지 기하학적으로 생각해 보자
만약 열벡터들이 다른 방향을 가지고 있을 때(역행렬 존재) 0이 아닌 벡터와 선형결합을 생각하면 결과 벡터가 0이 나올 수 없다.

위의 두개의 벡터의 크기를 조절(단, 0으로 스케일링은 안됨)하여 두 벡터의 합이 (0,0)을 가르킬 순 없다.
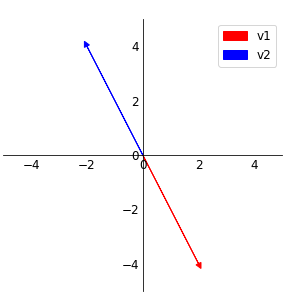
결과가 0벡터가 나오려면 같은 선형변환을 한 후 기저 벡터들이 같은 line에 위치한 경우만 해당이 되는데 위의 두 벡터의 크기를 조절하여 합이 (0,0)을 가르키는 것을 상상할 수 있다.
여기서는 v1과 v2벡터에 1배씩을 한 벡터의 합이 0벡터를 가르킨다.
위의 선형변환에서 설명했듯이 차원이 축소되면 역행렬을 가질 수 없는데, 그렇다고 만족하는 해가 없다는 것은 아니다. 위 처럼 같은 line에 존재하는 모든 벡터들이 0벡터로 향할 수 있는데 이런 집합을 null space라고 한다.
더 나아가 역행렬이 없다 하더라도 Ax=b형태에서 b가 기저벡터들의 같은 라인에 존재할 경우에는 만족하는 해를 찾을 수 있다.
[1236] A
행렬A도 같은 경우이다. 행렬 A는 x를 [3 -1]로 설정하면 0벡터가 된다.
만약 시스템 A가 역행렬이 있다면 A−1A=I가 될 것이다.
그렇다면 시스템 A가 벡터 x를 0으로 보냈는데 이 0벡터를 다시 원상복구 시켜줄만한 어떠한 행렬(A의 역행렬)이 존재한다는 말이다.
0벡터에 어떠한 연산(선형결합)을 해도 0벡터를 벗어날 수 없을 것 이다. 따라서 변수 자체가 0이 되어버렸으면 복원시킬 방법이 없으며 어떠한 행렬(역행렬)이 존재한다는 것 자체가 말이 안된다.
Gauss-Jordan idea
역행렬이 없는 경우에 대해서 알아 보았고 다시 역행렬이 존재하는 경우에서 역행렬을 구하는 방법을 알아보자.
[1237]
A
위의 행렬은 행렬식도 0이 아니고, 각 column벡터들은 서로 다른 방향을 가르키고 있으며 Ax=0을 만족하는 x를 찾을 수 없다.
따라서 A가 역행렬을 가질 수 있다는 것을 알았다. 그럼 역행렬을 어떻게 구할까?
[1237][acbd]=[1001]
A A−1 I
위의 식처럼 행렬A과 연산을 통해 단위행렬을 만드는 행렬이 존재해야 한다.
column-wise로 분리해서 보면 좀더 쉽게 이해할 수 있다.
[1237][ac]=[10]
[1237][bd]=[01]
위의 2개를 풀 수 있다면 행렬 A의 역행렬이 존재한다.
이 생각이 Jordan's idea의 시작이다.
이 식을 풀기 위한 방법으로 우리는 Gauss소거법을 이용할 것 이다. 소거법 과정에 우변의 extra column벡터를 추가하여 만든 행렬을 Augmented Matrix라고 한다.
소거법 과정에서 우변 벡터 하나만을 붙여서 계산했지만 여기에 column을 하나 더 붙여서 한번에 2개의 식을 풀어보는 방법을 사용한다.
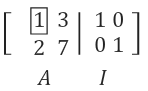
gauss소거법을 활용하며 소거행렬을 만들며 진행 한다. ( row-wise로 생각하면 쉬움 )
기준식에서 pivot을 그 아래의 원소들을 소거하기 위한 소거행렬을 만든다.
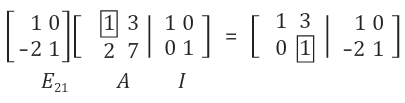
E21의 첫번째 row는 A행렬의 첫번째 row를 그대로 유지해야 하기 때문에 [1 0]이 된다.
E21의 두번째 row는 A행렬의 2행 1열의 요소를 소거해야 하기 때문에 [-2 1]이 된다.
단위행렬에도 똑같은 연산을 하게 되고, 단위행렬은 IA=AI=A의 특징을 가지고 있기 때문에 E21로 바뀐다.
gauss소거법은 상삼각행렬이 만들어진 지금 시점에서 끝났지만 jordan은 여기서 소거를 더 진행한다. pivot을 기준으로 아래에서 위쪽으로 소거를 진행한다.

결과적으로 행렬A로 부터 단위행렬을 만들었음을 볼 수 있다.
이때 사용한 소거행렬들이 바로 역행렬이 된다.

추가적으로 여기서는 pivot들이 자연스럽게 1로 되었지만 소거법을 진행하면서 pivot을 1로 바꾸기 위한 작업도 추가될 수 있다. 해당 row에 상수배를 해주어 1로 바꿀 수 있다.