막 쓰는 선형대수4 ( LU Decomposition )

모든 자료는 이곳에서 출처를 둠

LU Decomposition

LU Decomposition이란 어떤 행렬 A를 하삼각 행렬(L, Lowere triangular matrix)과 상삼각 행렬(U, Upper triangular matrix)로 분해하는 것을 말한다.

A를 L과 U로 분해할 수 있다면 $Ax=b$를 $LUx=b$로 표현할 수 있다.
결합법칙이 가능하기 때문에 $L(Ux)=b$에서 $Ux=y$로 치환한다면 $Ly=b$로 나타낼 수 있다.
$Ly=b$를 기존의 방식으로 풀어서 $y$를 구하고 $y$를 $Ux=y$에 대입하여 최종적인 해를 구한다.

LU 분해를 하는 이유는 무엇일까 ?

단순하게 방정식의 해를 구하기 위해서 이다.
그럼 $Ax=b$를 풀면 되는데, A를 L,U로 분해하여 더 복잡해 보일 수 있다. 하지만 계수행렬인 $A$는 바로 해를 구하기엔 너무 지저분한 숫자를 가지고 있다. 이 계수행렬을 L, U로 분해한다면 눈으로도 쉽게 해를 구할 수 있다.

우리는 이미 앞에서 가우스 소거법을 사용하여 우리는 $Ax=b$를 $Ux=c$형태로 바꾸는 법을 배웠다.

$\begin{bmatrix} 1&0&0\\ -3&1&0\\ 0&0&1\\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 1\\ 3 & 8 & 1\\ 0 & 4 & 1 \end{bmatrix}$

$E_{21}　　　　 A$

$\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&-2&1\\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 1\\ 0 & 2 & -2\\ 0 & 4 & 1 \end{bmatrix}= \begin{bmatrix} 1&2&1\\ 0&2&-2\\ 0&0&5\\ \end{bmatrix}$

$E_{32}　　　　 A　　　　　　　U$

$E_{32}(E_{21}A)=U\dashrightarrow(E_{32}E_{21})A=U\dashrightarrow EA=U$

위의 $EA=U$의 형태를 보면 $A=LU$의 형태와 비슷해 보인다. 어떻게 하면 $A=LU$의 형태로 바꿀 수 있을까?

$E$의 역행렬을 양변의 좌측에 곱해주면 된다.

$E^{-1}EA = E^{-1}U\dashrightarrow IA=E^{-1}U$
$E^{-1}$을 $L$로 나타낼 수 있으며 결과적으로 $A$를 $LU$로 분해할 수 있게 된다.

• LU분해의 특징

1. 모든 행렬이 LU분해가 가능한가 ?

   $\begin{bmatrix} 0&1\\ 1&0 \end{bmatrix}$

   위의 경우만 봐도 LU로 분해할 수 없다.
   만약 위의 행렬이 LU로 분해할 수 있다면

   $\begin{bmatrix} a&0\\ b&c \end{bmatrix} \begin{bmatrix} d&e\\ 0&f \end{bmatrix}= \begin{bmatrix} ad&ae\\ bd&be+cf \end{bmatrix}$

   로 나타낼 수 있는데, ad=0, ae=1 이므로 d=0이여야 한다. 하지만 bd=1이여야 하므로 모순이 생긴다.
   
   

2. 분해된 LU값은 유일한 값을 가지는가?
   
   아니다. A가 LU로 분해된다고 가정했을 때 L을 $L'DU$ ( LDU 분해)를 할 수 있고 결합법칙으로 $L'(DU)$를 $L'U'$으로 표현할 수 있다.
   
   

3. LU로 분해할 수 있는 경우는 ?
   
   행렬 A를 행교환 없이 가우스 소거하여 행사다리꼴의 형태로 만들 수 있는 경우 LU로 분해가 가능하다.
   
   위의 역인 A가 LU로 분해가 가능하다면 A를 행교환없이 행사다리꼴로 가우스 소거법이 가능한가?는 성립하지 않는다.
   

   $A= \begin{bmatrix} 0&0&0\\ 0&1&0\\ 3&0&0 \end{bmatrix}= \begin{bmatrix} 0&0&0\\ 0&1&0\\ 3&0&0 \end{bmatrix} \begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix}=LU$

행사다리꼴 (REF, Row Echelon Form)

이해를 위해 행사다리꼴이 무엇인지 알고가자.

정방행렬이 아닌 직사각행렬에서 row operation을 통해 얻은 결과물로 마치 상삼각행렬과 같은 형태일 수 있다.

• 0이 아닌 모든 행은 모든 행이 0인 행 위에 있다. ( 모두 0인 행은 맨 아래에 있어야 한다.)

• 0이 아닌 행의 선행 계수는 항상 위 행의 0이아닌 첫 번째 항목(leding entry)의 오른쪽에 있다.

• 피벗 아래의 모든 열 항목은 0이다.

이 상태에서 피벗 값들을 전부 1로 바꾸고 피벗의 위의 숫자들도 모두 0으로 만들어주면 이 행렬을 기약행사다리꼴(RREF, Reduced Row Echelon Form)이라고 한다.

사다리꼴이라고 번역이되서 우리가 생각하는 사다리꼴 도형을 떠올리면 더 어렵게 다가올 수 있다. echelon이라는 단어가 사다리라는 뜻을 가지고 있지만 여기서 의미하는 echelon form은 step-like architecture를 의미한다.
즉 마치 행렬의 하단에 0으로 이루어진 행이 있다보니 계단의 형태를 띄고 있다고 생각하는게 더 쉽게 이해할 수 있다.

행렬 A를 가우스 소거법을 적용하여 상삼각행렬을 구하는것이 REF와 같다고 볼 수 있다.

LDU Decomposition

LU 분해와 매우 유사한 행렬 분해이다.
LDU 분해를 할 때 가정할 것은, 행렬 A가 가역행렬이라는 가정이다.

행렬 A를 LU로 분해 했을 경우,

또는

과 같이 분해할 수 있을 것이다.

이런 경우 각각 L 또는 U의 1이 아닌 피벗값들만 따로 분리하여 행렬을 만들고 싶을 때 우리는 LDU로 분해할 수 있다.

첫번째 식의 경우

$L　　　 D　　　 U$

두번째 식의 경우

$L　　　 D　　　 U$
로 분해할 수 있다.

위의 결과에서 알수 있는것처럼 행렬 A를 LU로 나타낼 수 있는 것은 유일하지 않지만
LDU를 사용하는 큰 장점은 유일하다는 것이다.

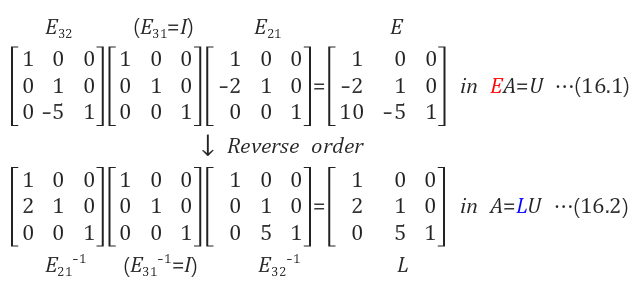
위의 계산에서 알수 있듯이, A = LU분해에서 행교환이 없다면, 소거행렬들의 각자 위치 그대로 하삼각행렬이 만들어진다.

PLU Decomposition

LU분해와 LDU분해를 할 때, 행교환없이 가우스 소거법을 한다는 조건이 있었다.

일반적으로 행렬 A는 행교환없이 가우스 소거를 했을 때, 행사다리꼴을 얻을 수 있는 것은 아니다.

이런 경우를 위해 LU분해를 하기전 사전에 전처리 작업이 필요하다. LU분해를 하기 전에 미리 $Ax=b$라는 선형시스템에 행교환을 진행하는 작업이 필요하다.

즉 행교환에 해당하는 치환행렬(Permutation Matrix)을 양변에 곱해주는 작업이다.

$Ax=b \dashrightarrow PAx = Pb$

위의 전처리를 거치면 행교환없이 가우스 소거하여 행사다리꼴을 얻을 수 있는 행렬 $PA$를 계수로 가지고 있는 시스템을 만들 수 있다.

전처리를 거쳐도 위의 시스템의 해는 동일하다.

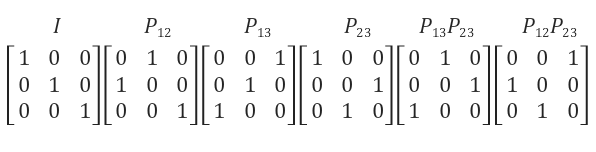
전 시간에 잠깐 언급했던 치환행렬에 대해서 알아보자.

$P_{12}$의 경우 P는 Permutations의 약자이고 아랫첨자는 1행과 2행을 교환하겠다는 의미이다.

$P_{12}$를 적용하고 다시 원상복구하려면 역행렬을 곱해야한다. $P_{12}$의 역행열을 무엇일까?
1행과 2행을 교환하는 치환행렬을 다시 원상복구 시키려면 1행과 2행을 다시 교환해주면 된다. 즉, $P_{12}$가 역행렬 그 자체가 된다.

$P_{13}P_{23}$과 $P_{12}P_{23}$도 역행렬, 전치 관계에 있는 것을 알 수 있다.

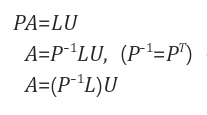
모든 A행렬을 PA로 표현할 수 있다. ( 행교환이 없다면 P는 단위행렬이 될 것 이다.)

• Permutation Matrix 특징

1. 모든 P행렬은 invertible 하다. ( 역행렬이 존재하는 단위행렬에서 행만 바꿨음 )

2. P행렬의 역행렬은 전치행렬과 같다.