트리 ?

출처 : 네이버 지식백과
트리구조는 배열구조 또는 자료구조 (1)의 Linked list와 비슷하게 노드(Node)라는 개념을 이용해서 구현할 수 있다. 데이터의 양이 많고 데이터의 삽입과 삭제가 유동적이면 Linked list, 데이터 양이 정해져있으며 컨트롤 할 수 있으면 배열로 구현한다.
트리구조에서 사용하는 용어를 정리해보자.
-
Root Node : 부모가 없는 노드이며, 트리의 가장 위에 있는 노드를 말한다. 트리구조에서는 단 한개의 루트 노드를 가진다. ( A )
-
Leaf Node : 말단 노드는 자식 노드가 없는 노드이다. ( G,H,I,E,J,K,L )
-
Sibling : 같은 부모를 가지는 노드를 말한다.
-
Edge : 노드와 노드를 연결하는 선을 말한다.
-
Degree
- 노드의 차수 : 자식 노드의 개수 ( A : 2 , B : 3 )
- 트리의 차수 : 모든 노드의 차수 중 가장 큰 값 ( 3 )
-
Depth : 루트에서 노드 까지의 간선의 개수 ( B : 1 )
-
Level : 특정 깊이를 가지는 노드의 집합 ( A : 1, { B, C } : 2 )
-
트리의 height : 트리에서 가장 깊은 Level ( 4 )
-
Size : 자신을 포함한 모든 자식노드의 개수 ( 트리의 size : 12, B : 6 )
트리구조는 데이터를 어떻게 삽입하고 삭제하는 것에 대해 초점이 잡힌 게 아니라, 데이터를 어떻게 표현할지에 초점이 잡혀있다는 것을 인지하는 것이 좋다.
이진트리 ( Binary Tree )
이진트리는 하나의 노드에 최대 2개의 서브트리가 있는 노드를 의미한다.
각각의 서브트리의 노드는 부모의 왼쪽, 오른쪽 자식인지 지정된다.
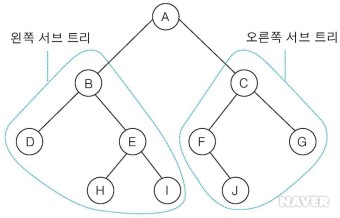
출처 : 네이버지식백과
이진트리의 종류
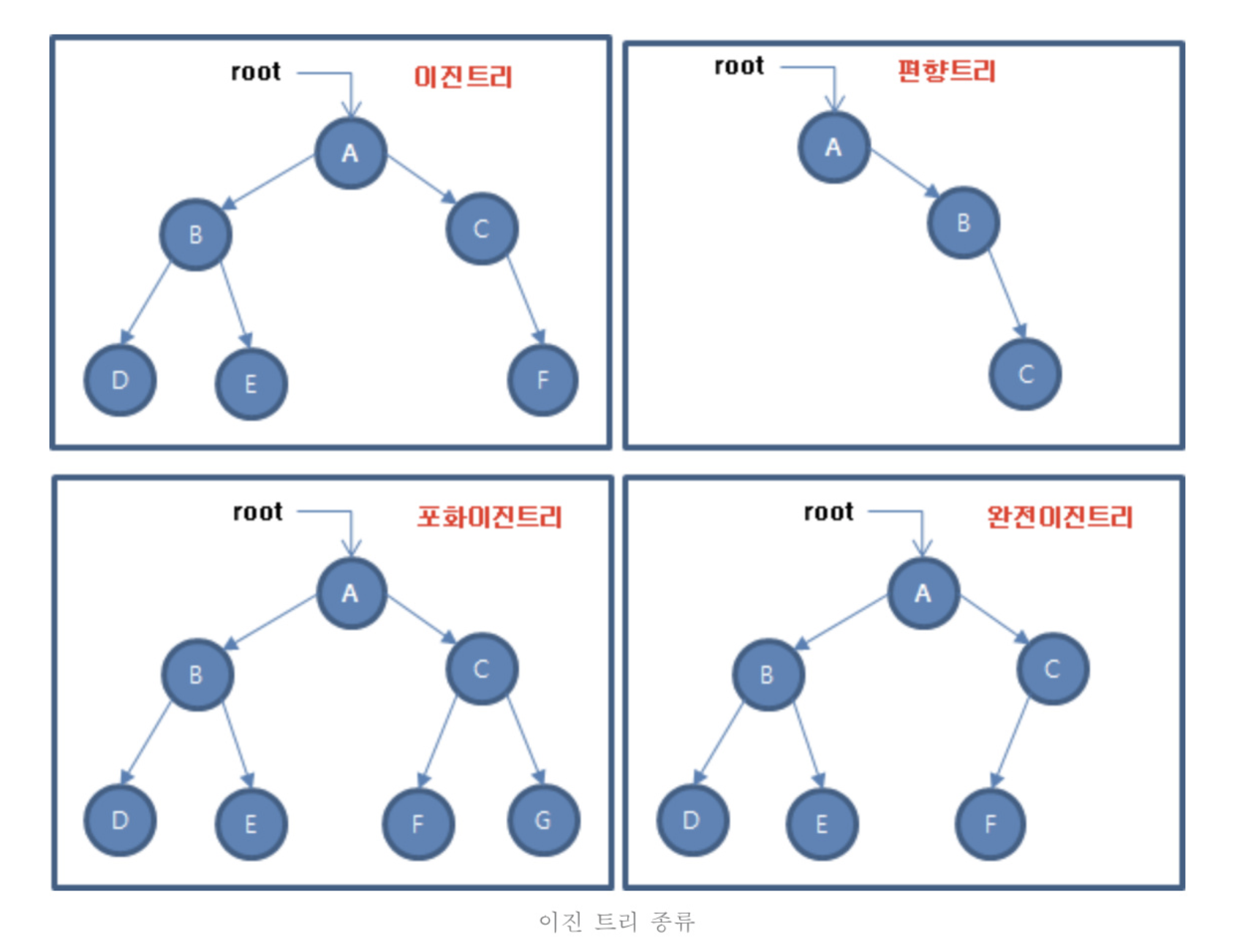
- 포화 이진 트리 ( Perfect binary tree )
- 모든 레벨의 노드가 차있는 구조
- 노드의 개수 n : 2^h - 1 ( h = 높이 )
-
전 이진 트리 ( Full binary tree )
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리

- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
-
완전 이진 트리 ( Complete binary tree )
- 마지막 레벨 전까지 차있는 구조
- 마지막 레벨은 꽉 차 있지 않아도 되지만 왼쪽에서 오른쪽으로 채워져 있어야 된다.
- heap과 관련이 있는 구조
-
편향 이진 트리 ( Skewed binary tree )
- 왼쪽 또는 오른쪽으로 편향되어 차있는 구조
- 각 레벨에서 1개의 노드만 있다.
-
균형 이진 트리 ( Balanced binary tree )
-
모든 노드의 왼쪽과 오른쪽 서브 트리의 높이가 1이상 차이 나지 않는 구조
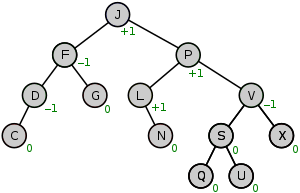
-
-
이진 검색 트리 ( Binary search tree )
-
어떤 노드(N)를 기준으로 왼쪽 서브트리의 노드의 모든 값은 노드 N의 값보다 작야아 한다.
-
오른쪽 서브트리 노드의 값은 노드 N의 값보다 커야한다.
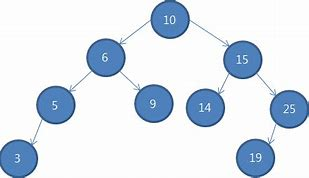
-
순회 ( traversal )
-
층별 순회 ( levelorder traversal )
- 레벨별로 순회를 하는 구조
-
전위 순회 ( preorder traversal )
- root부터 부모 노드의 왼쪽 자식 노드부터 순회하고 오른쪽 자식 노드를 순회하는 구조
( ROOT - L - R )
- root부터 부모 노드의 왼쪽 자식 노드부터 순회하고 오른쪽 자식 노드를 순회하는 구조
-
중위 순회 ( Inorder traversal )
- 왼쪽 하위 노드부터 시작해 부모노드 오른쪽 자식 노드를 순회하는 구조 ( L - ROOT - R )
-
후위 순회 ( Postorder traversal )
- 왼쪽 하위 노드부터 시작해 오른쪽 자식노드 부모노드를 순회하는 구조 ( L - R - ROOT )
Python 구현 : Binary Tree
class Node:
def __init__(self,data):
self.data = data
self.left = None
self.right = Nonde
class BinaryTree:
def __init__(self):
self.root = None
## 부모노드와 자식노드들로 트리를 만든다.
def make_tree(self,node,L_node,R_node):
if self.root is None:
self.root = node
node.left = L_node
node.right = R_node
## 레벨별 순회
def levelorder(self):
# root가 없으면
if self.root is None:
return -1
else:
## 층별순회를 하기위한 Queue역할의 배열생성
Q = [self.root]
print('레벨 순회',end=' :')
while Q:
tmp = Q.pop(0)
if tmp is None:
break
Q.append(tmp.left)
Q.append(tmp.right)
print(tmp.data,end=' ')
## 전위 순회 ( Root - L - R )
def preorder(self,node):
print(node.data, end=' ')
if node.left != None: self.preorder(node.left)
if node.right != None: self.preorder(node.right)
## 중위 순회 ( L - Root - R )
def inorder(self,node):
if node.left != None: self.inorder(node.left)
print(node.data, end = ' ')
if node.right != None: self.inorder(node.right)
## 후위 순회 ( L - R - Root )
def postorder(self,node):
if node.left != None: self.postorder(node.left)
if node.right != None: self.postorder(node.right)
print(node.data,end=' ')
if __name__ == '__main__':
nodes = []
nodes.append(Node(1))
nodes.append(Node(2))
nodes.append(Node(3))
nodes.append(Node(4))
nodes.append(Node(5))
nodes.append(Node(6))
nodes.append(Node(7))
BT = BinaryTree()
for i in range(int(len(nodes)/2)):
BT.make_tree(nodes[i],nodes[2*i+1],nodes[2*i+2])
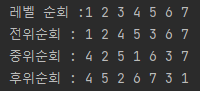
BT.levelorder()
print('\n전위순회 :',end =' ') ;BT.preorder(BT.root)
print('\n중위순회 : ',end = '') ;BT.inorder(BT.root)
print('\n후위순회 :',end=' ');BT.postorder(BT.root)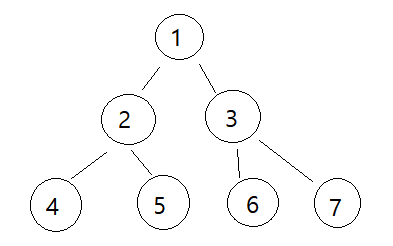
Python 구현 : binary search tree
이진탐색트리 ( Binary Search Tree )
이진탐색트리는 모든 노드에 대해 왼쪽 자식 노드들의 값이 현재 노드 값보다 작거나 같고 오른쪽 자식 노드들의 값이 현재 노드 값보다 크다는 조건이 있는 트리 구조이다.
class Node:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
# 데이터 삽입
def insert(self,data):
self.root = self.insert_data(self.root,data)
return self.root is not None
def insert_data(self,node,data):
if node is None:
node = Node(data)
else:
if data <= node.data:
node.left = insert_data(node.left,data)
else:
node.right = insert_data(node.right,data)
return node
# 데이터 탐색 ( 존재 유무 )
def find(self,data):
return self.find_data(self.root,data)
def find_data(self,root,key):
if root is None or root.data == key:
return root is not None
elif key < root.data:
return self.find_data(root.left,key)
else:
return self.find_data(root.right,key)
# 데이터 삭제
def delete(self,data):
'''
노드의 자식이 없으면 상관없지만, 노드의 자식이 하나인 경우 그 자식 노드를
삭제할 노드 위치로 옮겨준다. 노드의 자식이 두개인 경우는 ?
삭제할 노드 기준 왼쪽 서브트리 : A
삭제할 노드 기준 오른쪽 서브트리 : B
B의 가장 왼쪽 아래에 위치한 노드를 가져온다.
A의 모든 원소보다 크며 B의 나머지 원소들 보다 작기 때문이다.
'''
self.root , deleted = self.delete_value(self.root,key)
return deleted
def delete_value(self,node,key):
if node is None:
return node,False
deleted = False
if key == node.data:
deleted = True
# 자식이 둘다 있을 경우
if node.left and node.right:
#오른쪽 서브트리의 맨 왼쪽아래 노드
par , chi = node, node.right
while chi.left is not None:
par , chi = chi , chi.left
# chi이 왼쪽 맨 아래 노드 ( chi의 left에 node의 왼쪽서브트리 연결 )
chi.left = node.left
# chi 노드의 오른쪽 값들을 par.left에 연결
if par != node:
par.left = chi.right
chi.right = node.right
node = chi
#삭제할값이 노드보다 작은경우
elif key < node.data::
node.left, deleted = self.deleted_value(node.left,key)
#삭제할값이 노드보다 큰경우
else:
node.right, deleted = self.delete_value(node.right,key)
return node, deleted