[ 자료구조 ] 힙

힙 ?

힙(Heap)구조란 완전 이진 트리의 일종으로 어떤 데이터 중 최대값이나 최소값을 빠르게 찾아내도록 만들어진 구조이다.

부모노드의 키 값이 자식노드의 키 값보다 큰(작은) 관계가 유지되어 트리 내에서 가장 큰(작은) 키 값을 가진 노드는 항상 루트노드가 된다.

• 최소 힙 (Min Heap) : 부모노드의 키 값이 자식노드의 키 값보다 항상 작다.
• 최대 힙 (Max Heap) : 부모노드의 키 값이 자식노드의 키 값보다 항상 크다.
• 힙 구조는 형제 노드간의 정렬 상태가 없다. 따라서 루트값에 있는 제일 큰(작은) 값은 알 수 있지만 두번째로 작은 값은 인덱스로는 알 수 없다.

※ 최소 힙을 이해하면 최대 힙은 숫자만 반대로 된 것이기 때문에 최소 힙으로 힙 구조를 이해하기.

힙의 데이터 삽입

• 최소 힙은 루트 노드가 완전 이진 트리내에서 가장 작은 값은 같는다.

• 완전 이진 트리 구조를 지키기 위해 부모노드의 왼쪽 부터 채워 간다.

• 부모노드와 비교해서 삽입된 값이 작을 경우 부모노드와 위치를 교체한다.

• 부모노드와 비교하는 과정을 반복해서 부모노드 보다 값이 작거나 루트에 도착할 때까지 반복한다.

힙의 데이터 삭제

• 힙의 구조는 가장 작거나 큰 값을 찾기 위한 구조이기 때문에 루트 노드의 값을 빼내는 경우만 생각한다.

• 루트노드의 값이 비워져 있는 경우 이 루트를 채워주기 위해 완전 이진 트리의 맨 마지막 노드를 가져와서 루트에 채워준다.

• 자신의 자식 노드와 비교해서 자신 보다 작은 노드와 자리를 교체한다.

• 위의 과정을 반복하여 자식 노드보다 값이 작거나 leaf노드에 도착할 때까지 반복한다.

삽입과 삭제는 ( O(logn) )의 시간복잡도를 보인다.

Python 구현

class MinHeap:
    def __init__(self):
        self.queue = None


    def heapify(self,arr):
        self.queue = arr
        for i in range(len(arr)//2,-1,-1):

            self.__Min_heapify(i)

    ## 배열을 힙구조로 변환
    def __Min_heapify(self,i):

        left_i = self.child_left(i)
        right_i = self.child_right(i)
        cur_pointer = i

        if left_i <= len(arr)-1 and arr[cur_pointer] > arr[left_i]:
            cur_pointer = left_i

        if right_i <= len(arr)-1 and arr[cur_pointer] > arr[right_i]:
            cur_pointer = right_i

        if cur_pointer != i:

            self.swap(i, cur_pointer)
            #자신의 자식노드들까지 다 확인하기위해 재귀
            self.__Min_heapify(cur_pointer)


    def swap(self,i,parent_index):
        self.queue[i] , self.queue[parent_index] = self.queue[parent_index],self.queue[i]

    def parent(self,i):

        return (i-1)//2

    def child_left(self,i):
        return i*2+1

    def child_right(self,i):
        return i*2+2

    def print_heap(self):
        print(self.queue)

    ## 제거 ( 루트노드 )
    def heappop(self):

        # if len(self.queue) == 1:
        #     return self.queue.pop()

        if len(self.queue) == 0:
            return print('empty')


        self.queue[0],self.queue[-1] = self.queue[-1],self.queue[0]
        root_value = self.queue.pop()
        self.__Min_heapify(0)

        return root_value

    # 삽입
    def heappush(self,data):

        self.queue.append(data)

        for i in range(len(self.queue)//2,-1,-1):

            self.__Min_heapify(i)


if __name__=='__main__':

    arr = [4,3,1,5,2]

    heap = MinHeap()
    heap.heapify(arr)
    # heap.print_heap()
    print(heap.heappop())
    heap.print_heap()

    print(heap.heappop())
    heap.print_heap()

    print(heap.heappop())
    heap.print_heap()


    print('1 push')

    heap.heappush(1)
    heap.print_heap()

    print('3 push')
    heap.heappush(3)
    heap.print_heap()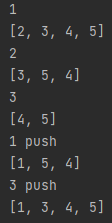

Python에서 heap라이브러리

import heapq

arr = [ 4,3,1,5,2]
print('배열 :',arr)
heapq.heapify(arr)
print('힙구조 :',arr)

heapq.heappop(arr)
print(arr)
heapq.heappush(arr,-1)
print(arr)

Tip

파이썬의 heap 라이브러리는 기본적으로 Min heap으로 제공한다.
Max heap을 구성하고 싶을 경우, -를 넣어 구성하거나

heapq.heappush(arr,(-data,data))식으로 구성하면 튜플의 0번 인덱스의 값으로 정렬되어
구성되고, 값을 불러올때는 1번 인덱스의 값을 불러오는 방법을 사용하자