ㅇ 교수 : KAIST 신진우 교수
ㅇ 학습목표
본 모듈은 AI기술을 이해하기 위한 바탕이 되는 수학적 지식을 학습하기 위한 과정입니다.
이에 관하여 행렬 분해, 블록 최적화, 주성분 분석 등 데이터를 다루기 위한 방법을 학습하게 됩니다.Part1. Matrix Decomposition (행렬분해)
Road Map
(1) Determinant and Trace
(2) Eigenvalues and Eigenvetors
(3) Cholesky Decomposition
(4) Eigendecomposition and Diagonalization
(5) Singular Value Decomposition
Summary
- How to summarize determinants and eigenvalues
- How matrices can be decomposed: Cholesky decomposition, diagonalization, singular value decomposition
1) Determinat: Motivation
Determinat = 정방행렬(nxn 행렬)
행렬식은 왜 배우는가?
역행렬의 존재 유무 파악, 역할 구하기 위해
2X2 정방행렬 det(A)
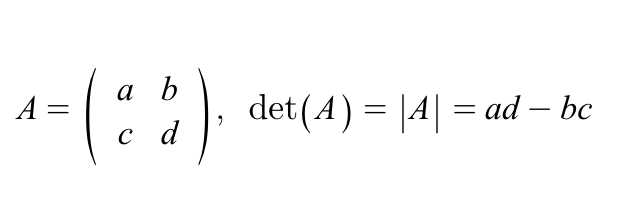
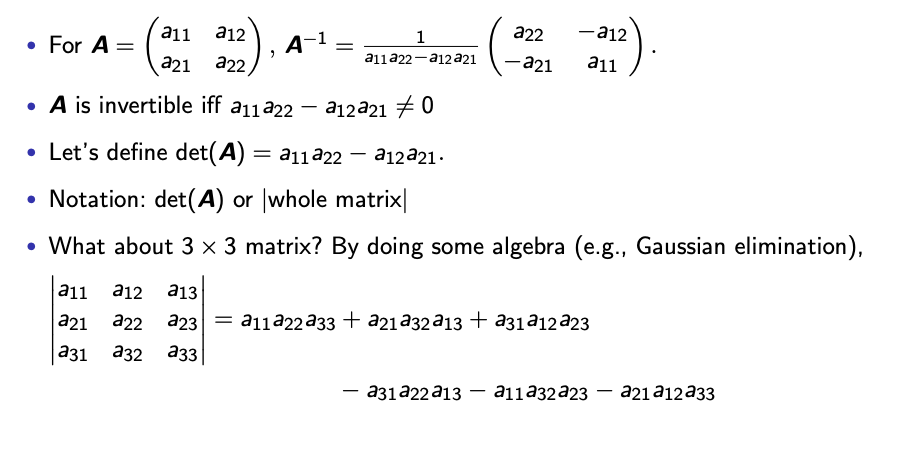
3X3 (Gaussian elimination)
3x3는 2x2로 표현 가능
이것을 Laplace expansion
Now, we can generalize this and provide the formal definition of determinant.
2) Formal definition
determinant
expansion along column
expansion along row
3) determinant: Properties
정방행렬(nxn 행렬)
Trace
정의: 합
tr(A+B) = tr(A) + tr(B)
Eigenvaule and Eigenvector
정의: Ax= λx
A=eigenvalue x= eigenvector
example
Properties
Determinant Eigenvector
Trace
4)Cholesky Decomposition
L = lower-triangular matrix with positive diagonals
AxA=LL^T
4) Diagonal Matrix and Diagonalization
Definition A = diagonalizalbe
Definition A = Orthogonally diagonalizable
Power of Diagonalization
Orthogonally Diagonaliable and Symmetric Matrix
Storyline
EVD = Eigen Value Decomposition
SVD = singular Value Decomposition
Background
Singular Value Decomposition
SVD : How It works
SVD(A= UEV^t) EVD(A= PDP^-1)
