비선형 구조
하나의 자료 뒤에 여러 개의 자료가 존재할 수 있는 형태
그래프(Graph)
정점(nodes,vertices)과 간선(edge,branch)으로 이루어짐
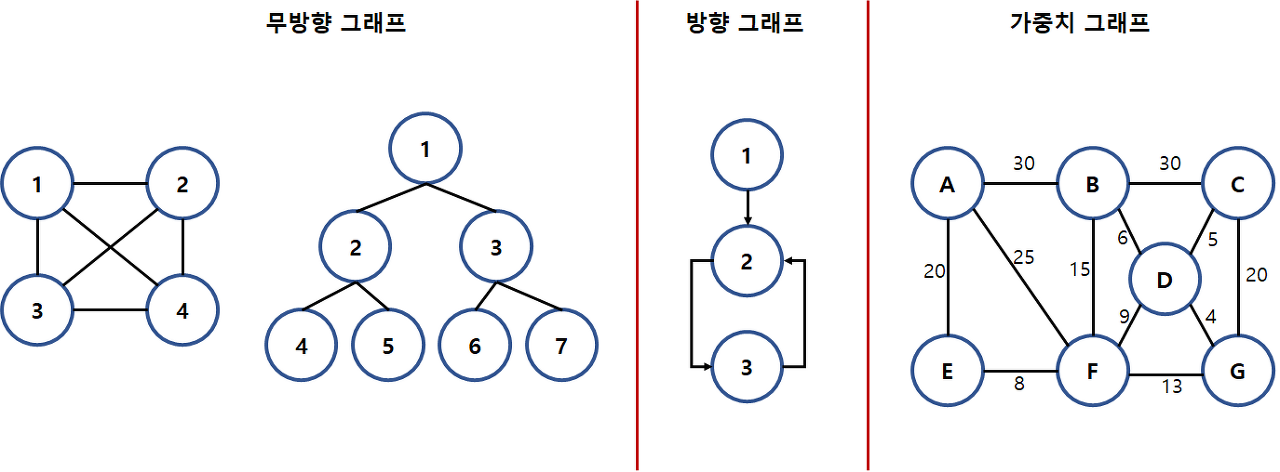
방향 그래프 : 진행방향이 정해진 그래프
가중치 그래프 : 이동할 때 비용이 정해진 그래프
사이클 : 처음 시작한 지점에서 정점들을 돌아서 처음 시작한 지점으로 돌아오는 것을 뜻함
ex) 무방향 그래프에서 1-2-4-1로 돌아올 수 있으므로 싸이클이 있다.
인접 행렬 / 인접 리스트
인접 행렬
그래프의 연결 관계를 2차원 배열으로 나타내는 방식
V : 노드의 총 개수
E : 간선의 개수
라고 했을 때
arr[i][j] : i에서 j로가는 간선이 있으면 1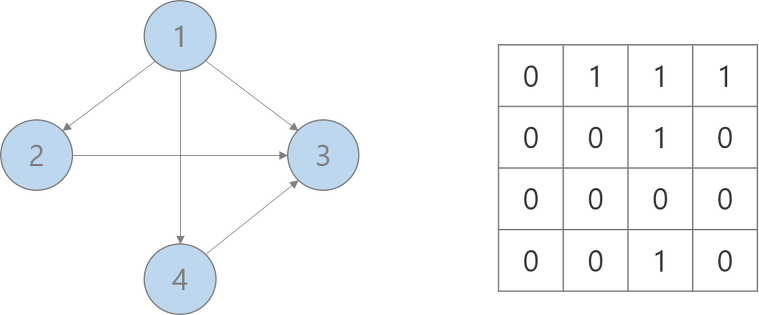
무향 그래프일 경우에는 아래처럼 대칭을 이루게 된다.
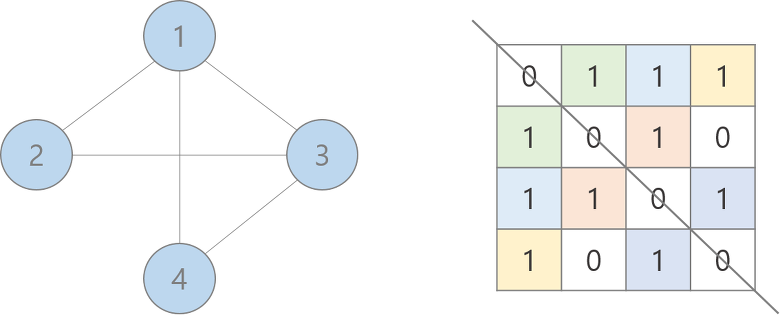
장점
- 구현이 쉽다.
- 특정 노드에서 특정 노드 연결이 되어있는 지 확인 쉬움
arr[i][j]<--- 확인하면 끝
단점
- 행렬을 전부 탐색해야하기 때문에 시간이 오래 걸림
- 특정 노드의 모든 노드 방문 원할 시 O(V)의 시간복잡도
- 모든 연결 확인 위해 O(V²)의 시간 복잡도
인접 리스트
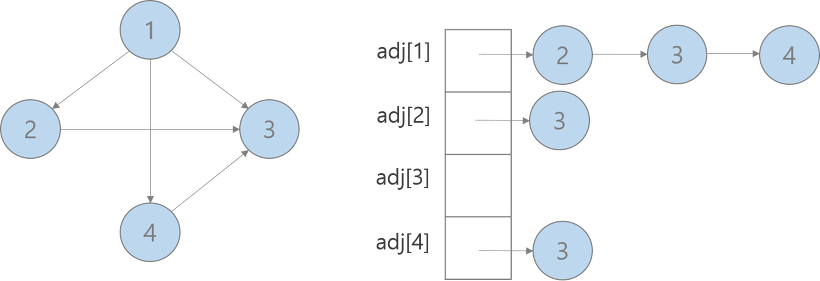
무향 그래프
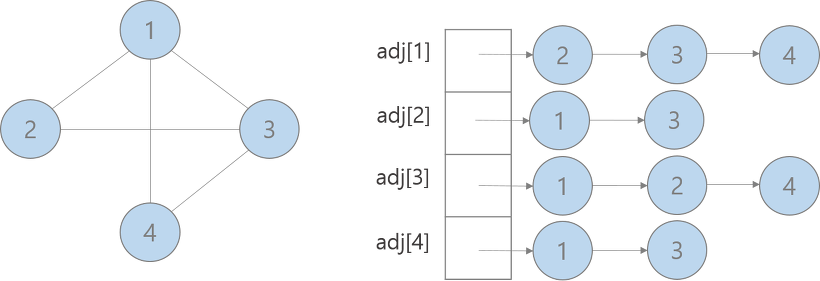
장점
- 실제 연결된 노드들에 대한 정보만 저장
- 따라서 간선 개수에 비례한 메모리 차지
- 모든 연결 확인 위해 O(E)의 시간 복잡도
단점
- 특정 노드에서 특정 노드 연결이 되어있는 지 확인하려면 O(V)의 시간복잡도
키워드 오일러 경로, DFS, BFS
트리(Tree)
트리를 정점과 선분을 이용해 사이클 없이 구성된 그래프
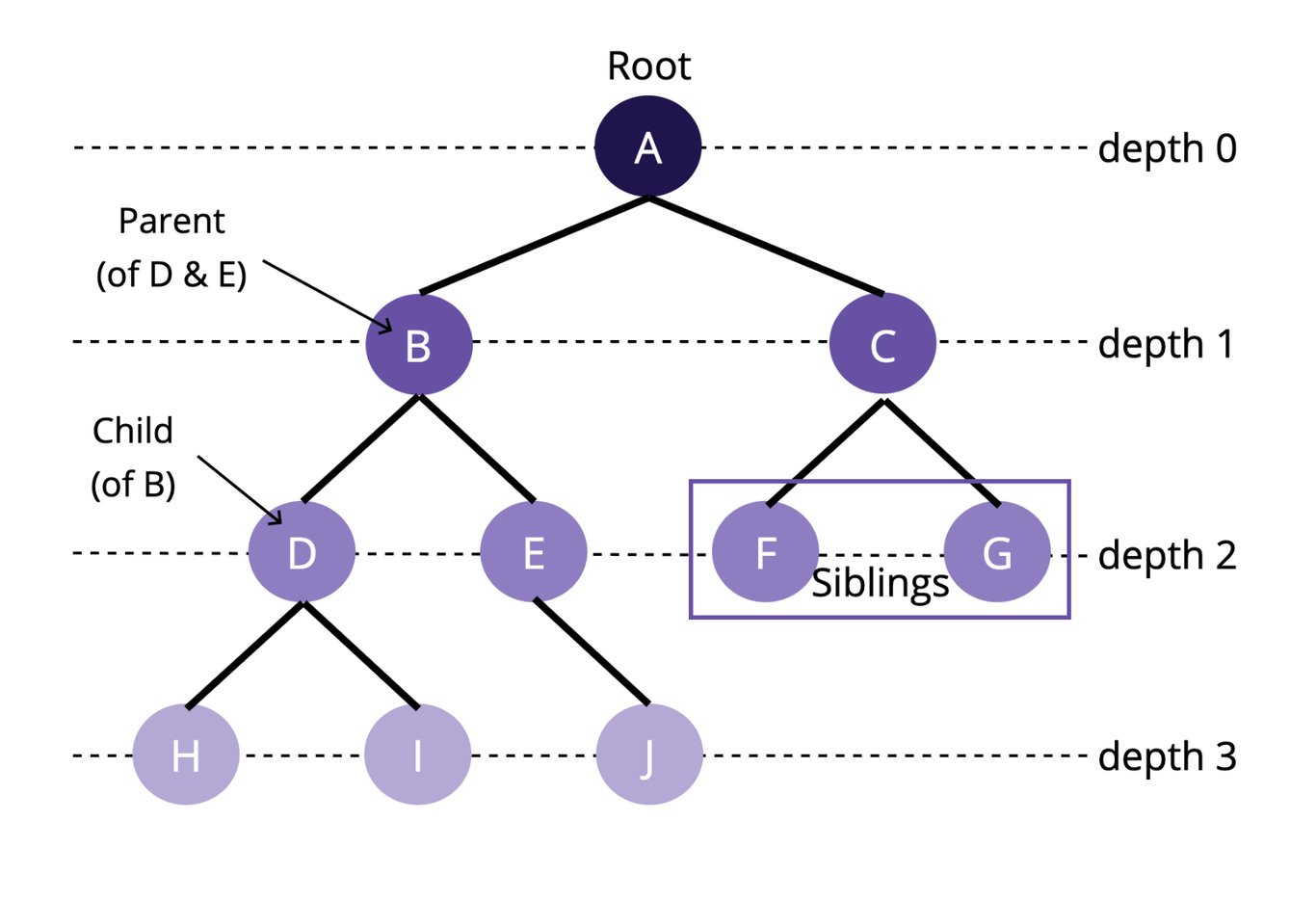
노드 : 트리의 구성 요소(A,B,C,D 등)\
Root : 최상위 노드
depth : Root를 기준으로 다른 노드로 접근하기 위한 거리
leaf : 자식이 없는 노드(최하위 노드)
A는 B,C의 부모 / B,C는 A의 자식
이진 트리(Binary Tree)
Root 노드를 포함, Leaf노드를 제외한 모든 노드의 자식이 최대 2개인 Tree
이진 탐색트리(BST, Binary Search Tree)
아래의 규칙을 지키는 이진트리르 뜻한다.
- 이진 탐색 노드에 저장된 값은 유일한 값이다
- 부모 노드 값은 왼쪽 각각 노드들 값보다 크다
- 부모 노드 값은 오른쪽 각각 노드들 값보다 작다.
키워드 : Rebalancing, Red Black Tree,
HashTable
Key-Value 값을 가진 배열 형태 자료구조
배열 구조로 되어있지만 해당되는 인덱스를 키 값과 해시 함수가 정해준다.
key -> hash function() -> index
key값을 넣으면 해당 인덱스를 바로 찾을 수 있다.
충돌 : key값이 다르지만 같은 index를 가리킬 때
충돌 해결 방법
- 체이닝
- 개방 주소방법
체이닝
같은 주소로 해싱되는 원소들을 연결리스트로 관리하는 방법이다.
추가 연결 리스트 필요
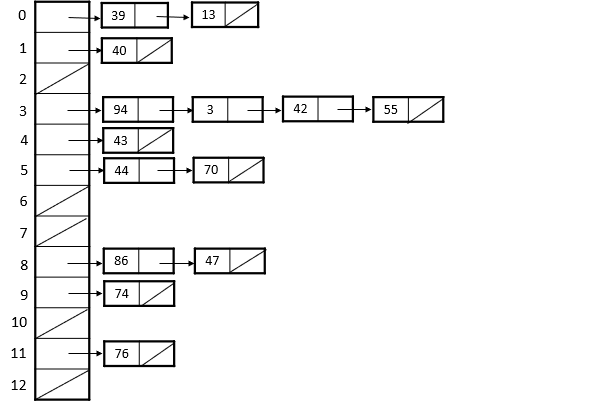
장점 : 계산한 해시주소에 해당하는 연결 리스트로 실행하기 때문에 빠르다
단점 : 주소의 쏠림현상이 일어날 수 있다.
개방 주소 방법
빈자리가 생길 때까지 해시값을 계속 만들어 냄
주어진 테이블 공간에서 해결하므로 추가 공간 필요 없음
선형 조사
- 해시값 중복 시 정해진 칸만큼 옆 값으로 이동 시킴
- 일차 군집화(특정 주소값 근처값이 모두 채워져 있다.)
이차원 조사
- 중복 시 1,2,3,...의 제곱으로 옆 값으로 이동시킨다.
- 이차 군집화
더블 해싱
- 해시 함수를 이중으로 사용하는 방법
- 첫 해시는 해시값을 얻기 위해 두 번째 해시는 충돌 시 탐사 이동 폭 얻기 위함
